基于多变量LSTM 神经网络模型的PDO 指数预测研究

于振龙，许东峰, ，姚志雄, ，杨成浩, ，刘松楠

(1.自然资源部第二海洋研究所 卫星海洋环境动力学国家重点实验室，浙江 杭州 310012；2.浙江省海洋科学研究院，浙江 杭州 310012；；3.自然资源部海洋空间资源管理技术重点实验室，浙江 杭州 310012)

1 引言

太平洋年代际振荡（Pacific Decadal Oscillation,PDO）是北太平洋年代际尺度上最主要的海表面温度（Sea Surface Temperature,SST）异常模态，PDO 的概念最早由Mantua 等[1]于1997 年首次提出，PDO 作为一种太平洋气候变化强信号，对太平洋及其周边地区气候变化有着重要影响。在PDO 暖相位期间，冬季阿留申低压加强，北太平洋呈现“马蹄形”的海表面温度异常，北太平洋中部偏冷，热带中东太平洋和北美沿岸偏暖；而在PDO 冷相位期间情况相反，北太平洋中部偏暖，热带中东太平洋和北美沿岸偏冷。PDO 指数被定义为太平洋20°N 以北海表面温度异常场经过经验正交函数分析（Empirical Orthogonal Function Analysis,EOF）第一模态的时间系数，其正、负分别代表了PDO 的暖、冷位相。PDO 作为主要的年代际气候变异之一，对太平洋动力环境、渔业收获[1-3]和我国的降雨[4-5]、气温[6-7]、农作物产量[8]以及南海的盐度变化[9-10]等有重要影响，所以PDO 的预测就显得尤为重要。

由于PDO 的复杂性以及全球变暖背景下PDO 的可预测性正逐渐降低[11]，预测PDO 的相位变化对于人们来说仍具有很大的挑战性。前人做过很多关于PDO 形成机理以及PDO 指数重建的研究：Mantua等[1-2]重点分析了PDO 的时间、空间特征，并定义PDO年代际指数是由PDO 指数5 年滑动平均获得。Yasuda[12]利用树木年轮和太平洋珊瑚数据对PDO 指数进行了气候重建。MacDonald 和Case[13]利用加利福尼亚和阿尔伯塔的柔枝松的水文敏感年轮年表重建了公元993-1996 年的PDO 指数时间序列，同时评估了PDO 强度和周期的长期变动特征。赵传湖等[14]利用东亚地区高分辨率的气候代用指标，通过双重检验的逐步回归方法和小波分析等方法，重建了近400年来的北太平洋PDO 指数，并分析了PDO 周期的演变特征。结果表明，北太平洋PDO 具有准20 年和准50～70 年的变化周期。Chen 等[15]通过模型数据比较，探讨了千年尺度PDO 变率，并利用北太平洋副热带海温的东西向差异以及东亚地区与PDO 相关的降水异常重建了PDO 指数。Schneider 和Cornuelle[16]指出，PDO 不是单一模式，而是多个物理过程的组合，PDO 的位相转变源于Niño 3.4 的强迫作用以及阿留申低压和黑潮-亲潮延伸体海区变化的累积，并进一步估算了这些影响因子对PDO 的相对贡献。与Schneider 和Cornuelle[16]的结论一致，Newman 等[17]分析了驱动PDO 的因素，改进了以前的PDO 经验模型[18]。Huang 和Wang[19]利用海表面高度、海平面压力和海冰密集度，通过“年际增量法”将变量的年际增量作为预测对象，实现了对PDO指数的后报。Lu 等[20]利用一种气候网络分析的新技术来捕获PDO 相位转变的前兆。通过计算PDO空间格局冷区和暖区之间的联系，在相位转变前几年，发现冷暖区域之间的负相关逐渐增强。该信号从1890 年到2000 年捕获了6 个PDO 相位转变，提前预警时间平均为（6.5±2.3）年。

PDO 是多个物理过程综合作用的结果。其中，大气强迫超前于海表温度变率，是影响北太平洋温度变率的主要因素。阿留申低压通过影响北太平洋地区水汽输送[21]，间接影响北太平洋温度，是驱动PDO 变率的主要大气强迫之一；PDO 相位的改变影响风场[22]和温度场，进而带来海表面高度的变化[23]；热含量（Ocean Heat Content，OHC）是表征海洋热状态的一个重要参数[24]，海洋主要的热量存储于0～700 m 水层[25-26]。大西洋多年代际振荡（Atlantic Multi-Decadal Oscillation,AMO）可以通过大气遥相关影响太平洋副热带热量分布，进而影响PDO[27-28]；北极涛动（Arctic Oscillation,AO）在PDO 低频变化中起着重要的作用，AO 增强会导致阿留申低压增强，进而通过北太平洋海气相互作用影响PDO[29]。格陵兰海冰可以通过影响AO 来影响PDO 变率，海冰密集度可以用来表征海冰的变化[30]。综上所述，海平面气压、海表面高度、热含量和海冰密集度均可作为PDO 指数的预报要素进行建模。

随着人工智能技术的发展，机器学习被应用于各个领域的研究[31-33]，深度神经网络成为了一种新型的研究手段。对于时间序列的预测应用最多的是循环神经网络（Recurrent Neural Network，RNN）模型，由于RNN 模型结构比较简单，使用的反向传播（Back Propagation Through Time，BPTT）算法不能适应长时间序列数据的训练，容易产生梯度爆炸以及梯度消失的问题，无法实现长期记忆的效果。因此，需要一个含有存储单元、存储记忆功能的神经网络模型。1997 年长短期记忆（Long Short Term Memory，LSTM）神经网络模型由Hochreiter 和Schmidhuber[34]提出。LSTM 神经网络模型是RNN 模型的改进，通过增加记忆单元里的控制门限来解决RNN 模型短期记忆的问题，从而可以高效地处理长时间序列信息，实现对复杂函数的建模。目前，国内外利用LSTM 神经网络模型对ENSO 预报的研究比较多[35-37]，与其他统计预报模型相比，LSTM 神经网络模型在长时间序列上具有较强的预报能力。由于年代际变化信号的预测比较困难，部分学者主要利用气候模型实现对PDO 指数的后报试验[38-39]，利用深度学习的研究还比较少。本文旨在前人研究基础上，将海平面气压、海表面高度、海冰密集度作为PDO 指数的预报要素，新增0～700 m 水层的热含量作为预报因子，建立LSTM 神经网络模型，实现对PDO 指数的预测，为PDO 指数的预测研究提供一种新的手段。

2 研究方法

2.1 LSTM 神经网络模型

LSTM 神经网络模型在本质上是RNN 模型的改进版本，其与RNN 模型最大的区别是增加了3 个逻辑控制单元（即控制门，包括输入门、输出门和遗忘门）来解决RNN 模型短期记忆问题，通过改变神经网络的记忆单元与其他部分连接的权值大小来控制信息流的输入、输出以及记忆单元的状态。其中输入门（input gate，记为it）用来控制信息是否能够被记录到记忆单元中；输出门（output gate,记为ot）控制当前时间节点记忆单元中的信息是否能够流入到当前隐藏层中；遗忘门（forget gate,记为ft）选择性遗忘上一时刻记忆单元的信息并累加到当前时刻记忆单元中。LSTM 神经网络模型结构示意图如图1 所示，其中，Xt为当前状态下数据的输入，ht为当前隐藏层，σ 和 tanh为当前记忆单元中两个不同的激活函数，“×”和“＋”分别代表矩阵相乘和矩阵相加运算。

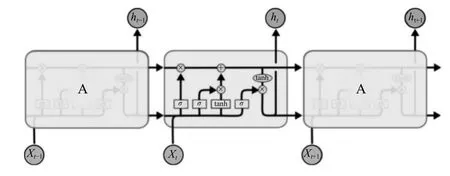
图1 LSTM 神经网络模型结构示意图（来源于文献[34]）Fig.1 Schematic diagram of LSTM neural network model structure (from reference [34])

在LSTM 神经网络模型的训练过程中，首先模型把t时刻的数据特征信息输入到输入层中，经过激活函数得到输出结果。然后将输出结果、t-1 时刻的记忆单元存储信息和t-1 时刻隐藏层输出结果输入到当前LSTM 神经网络模型结构处理单元中，通过3 个控制门限的处理后，输出结果将进入下一输出层和隐藏层，最后计算反向传播误差，更新各个递归连接权重的大小。在t时刻LSTM 神经网络模型每个记忆单元中的数据处理过程如式（1）～（6）所示：

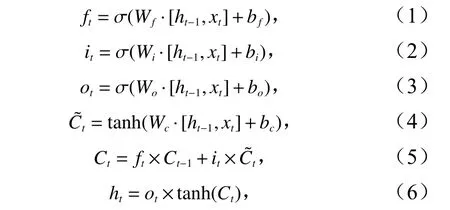
式中，ft、it、ot为3 个控制门限；Wf、Wi、Wo分别代表了其对应的控制门限的递归连接权重；bf、bi、bo是通过对应的控制门限误差值；ht代表t时刻隐藏层输出值；Ct代表当前神经元记忆状态的记忆单元，具有随着训练不断存储、读取、重置和更新长时间信息的能力。控制门结构由激活函数与点乘组成，公式中的激活函数 σ在0～1 之间取值，tanh 在-1～1 之间取值。点乘决定了记忆单元可以传送过去的信息量。激活函数的计算公式如式（7）和式（8）所示：

2.2 精度评估

利用PDO 预测值与观测值时间序列的均方根误差（RMSE）、平均绝对误差（MAE）和平均绝对百分比误差（MAPE）评价模型预测值与观测值的精度大小，计算公式为

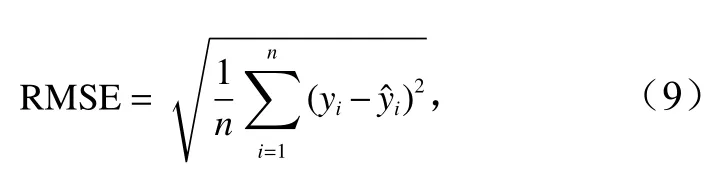
3 数据来源及处理

本文采用多个预报要素建立多变量LSTM 神经网络模型预测PDO 指数，实验流程如图2 所示。为了能够预测更长时间序列的PDO 指数，选取了1921-2020 年100 年的预报要素数据资料。除了海冰密集度数据以外，其他预报要素都选取了相同的研究区域（20°～60°N，120°E～100°W）。

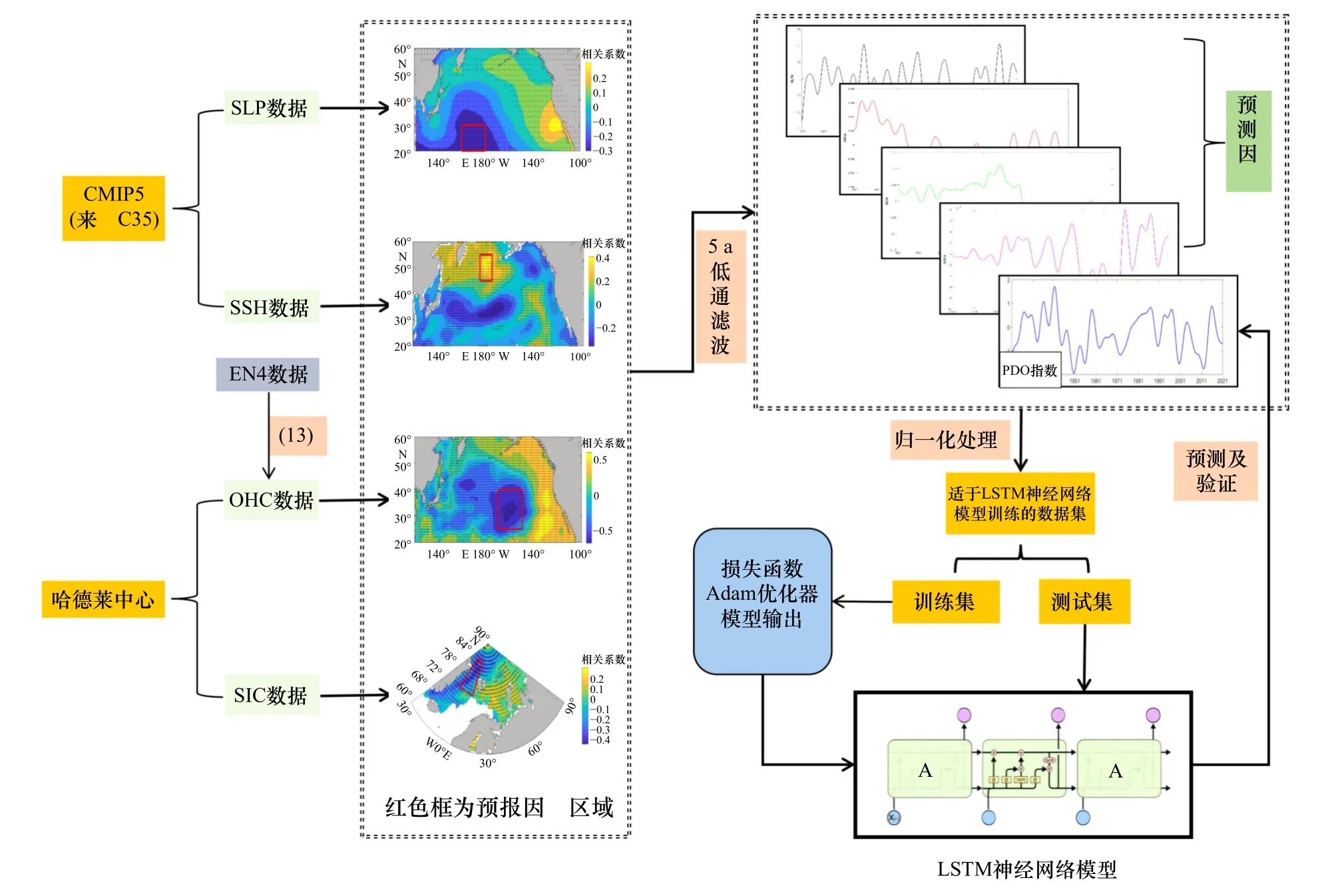
图2 实验流程图Fig.2 Experimental flowchart

首先，PDO 指数本文采用的是美国国家海洋和大气管理局（National Oceanic and Atmospheric Administration,NOAA）基于第五代版本ERSST 扩展重建的NCEI PDO 指数数据（https://www.ncdc.noaa.gov/teleconnections/pdo/）；海平面气压（Sea Level Pressure,SLP）数据源自哥白尼气候变化服务（Copernicus Climate Change Service，C3S，https://cds.climate.copernicus.eu/）的CMIP5 气候模式月平均数据，该数据由NOAA 的GFDL-CM2p1 模型计算而来，水平分辨率为2.5°×1.5°；海表面高度（Sea Surface Height,SSH）数据同样源自C3S 的CMIP5 模式数据，水平分辨率为1°×1°；海冰密集度（Sea Ice Concentration,SIC）数据源自英国气象局哈德莱中心的全球海冰和海表面温度数据集HadISST，水平分辨率为1°×1°。

热含量长时间序列数据获取相对困难，本文利用热含量计算公式获取1921-2020 年的热含量时间序列，所采用的数据为哈德莱中心的EN4 再分析温盐数据集。该数据集融合了WOD9、GTSPP、ASBO、GDACs 等数据集，并进行了质量控制。水平分辨率为1°×1°，时间分辨率为1 个月，深度共42 层，最深达5 000 m 以上。热含量计算方法为

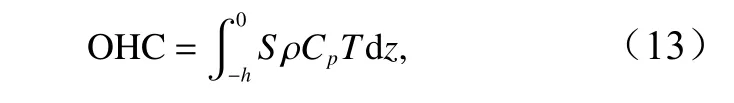
式中，OHC 为热含量，单位：J；S为数据网格的面积大小；ρ为海水的密度；Cp为定压比热容；T为海水温度；h为热含量计算水深（本文中h取为700 m）。

其次，采用相关性分析计算预报要素研究区域内的所有网格点时间序列与PDO 指数的相关系数，根据相关系数选取4 个预报区域，以下称“预报因子”，其中，SLP 选取的是20°～30°N，160°E～180°海域范围；SSH选取45°～55°N，175°E～175°W海域范围；0～700m的OHC选取25°～40°N，150°～170°W海域范围；SIC选取75°～85°N，10°W～10°E海域范围。100年的数据时间尺度会大大降低预报要素与PDO 指数的相关性，预报要素与PDO 指数的相关系数空间分布及预报因子区域范围如图3 所示，预报因子在区域内每个数据格点的时间变化与PDO 指数均满足99%置信水平的相关性。

图3 1921-2020 年预报要素与PDO 指数的相关系数Fig.3 Correlation coefficients of forecast elements and PDO index from 1921 to 2020

最后，计算预报因子的1921-2020 年的时间序列（异常），由于PDO 是年代际尺度上气候内部变率，周期通常为20～30 年，本文将PDO 指数数据利用Butterworth 低通滤波器进行了5 年的低通滤波处理，去掉高频变化信号得到PDO 指数，4 个预报因子的数据处理与PDO 指数相同，这样不仅能够让LSTM 神经网络模型预测更长时间尺度的PDO 指数序列，同时可以提升模型训练时的训练效率。图4 中从上到下依次是PDO 指数、海平面气压异常、海平面高度异常、0～700 m 热含量异常以及海冰密集度异常数据。

图4 太平洋年代际振荡（PDO）指数以及预报因子时间序列Fig.4 Pacific decadal oscillation index and predictor time series

4 模型训练与调参

本文全部数据采用归一化处理以消除量纲和数量级带来的影响，有利于提高预测模型的收敛速度和精度。多变量LSTM 神经网络模型预测时，预测的精度对模型参数的要求较大,不同的参数组合类型对模型的预测精度影响较为明显。LSTM 神经网络模型的性能取决于模型中超参数的设置，超参数是在模型训练前手动设定的训练变量，包括激活函数、优化器、批大小、训练轮数和隐藏层节点数。为了提高模型的训练效率，本文提前确定不重要的超参数：模型设定训练轮数为300 轮；学习率设置为0.005；使用自适应矩估计（Adaptive Moment Estimation,Adam）优化器不断更新训练网络权重以使损失最小。由于数据量大且为复杂矩阵，故调用GPU 进行训练加速。为了防止LSTM 神经网络模型出现过拟合的情况，通过在全连接层后添加随机失活（dropdout）层对在正相传递或权值更新过程中的LSTM 神经网络模型记忆单元进行优化，随机失活率的大小设置为0.2。

关于模型最优参数的确定，本文对隐藏层节点数、批大小以及学习率下降周期3 个超参数进行了组合调参，确保训练精度的同时也降低了模型训练的复杂程度。采用控制变量的方法，将隐藏层节点数分别取120层、240 层和360 层，批大小取60、120 和180，学习率下降周期取75、150 和225 轮，共27 种参数组合。每种参数组合在模型建立时都需要通过交叉验证（Cross Validation，CV），交叉验证是一种流行的具备鲁棒性的模型性能评估技术。本文建立的是关于PDO 指数时间序列的多变量多步LSTM 神经网络模型，训练集和测试集在逻辑上存在时间先后顺序，采用“递增时间窗交叉验证法”对模型进行交叉验证，方法如图5 所示。

图5 递增时间窗交叉验证法Fig.5 Incremental time window cross-validation

该交叉验证方法将PDO 指数数据等分成10 份，考虑到PDO 周期在20 年以上，本文将最小训练集设置为20 年。首先将前20 年（1921-1940 年）作为模型的训练集，后10 年（1941-1950 年）作为模型的测试集；将前30 年（1921-1950 年）作为模型的训练集，后10 年（1951-1960 年）作为模型的测试集；以此类推，直到将前90 年（1921-2010 年）作为模型的训练集，后10 年（2011-2020 年）作为模型的测试集。然后分别计算测试集中预测值与实际值的相关系数及均方根误差，模型训练5 次后取平均结果。最终将交叉验证的结果取平均作为该参数组合的交叉验证结果，通过对比不同参数组合的模型平均相关系数以及均方根误差大小，确定模型的最优参数并利用最优参数建立LSTM 神经网络模型，模型训练10 次取平均作为最终预报结果，最终将1921-2020 年的预报因子数据作为输入，实现对未来10 年的PDO 指数预测。

5 结果分析

多变量LSTM 神经网络模型调参的过程实际上是模型寻找靶心的过程，经过交叉验证，根据测试集与训练集相关系数（R）以及均方根误差（RMSE）确定模型的最优参数，可以最大程度地保证模型的靶心处于最佳位置。模型调参结果如表1 所示，拟合效果比较优异，所有参数组合测试集平均相关系数都在0.6～0.7 之间。其中，隐藏层节点数为360，批大小为180，学习率下降周期为75 轮的模型的平均相关系数为0.697 2，均方根误差为0.622 1，选取该参数组合作为模型训练的最优参数，已在表1 中粗体显示。

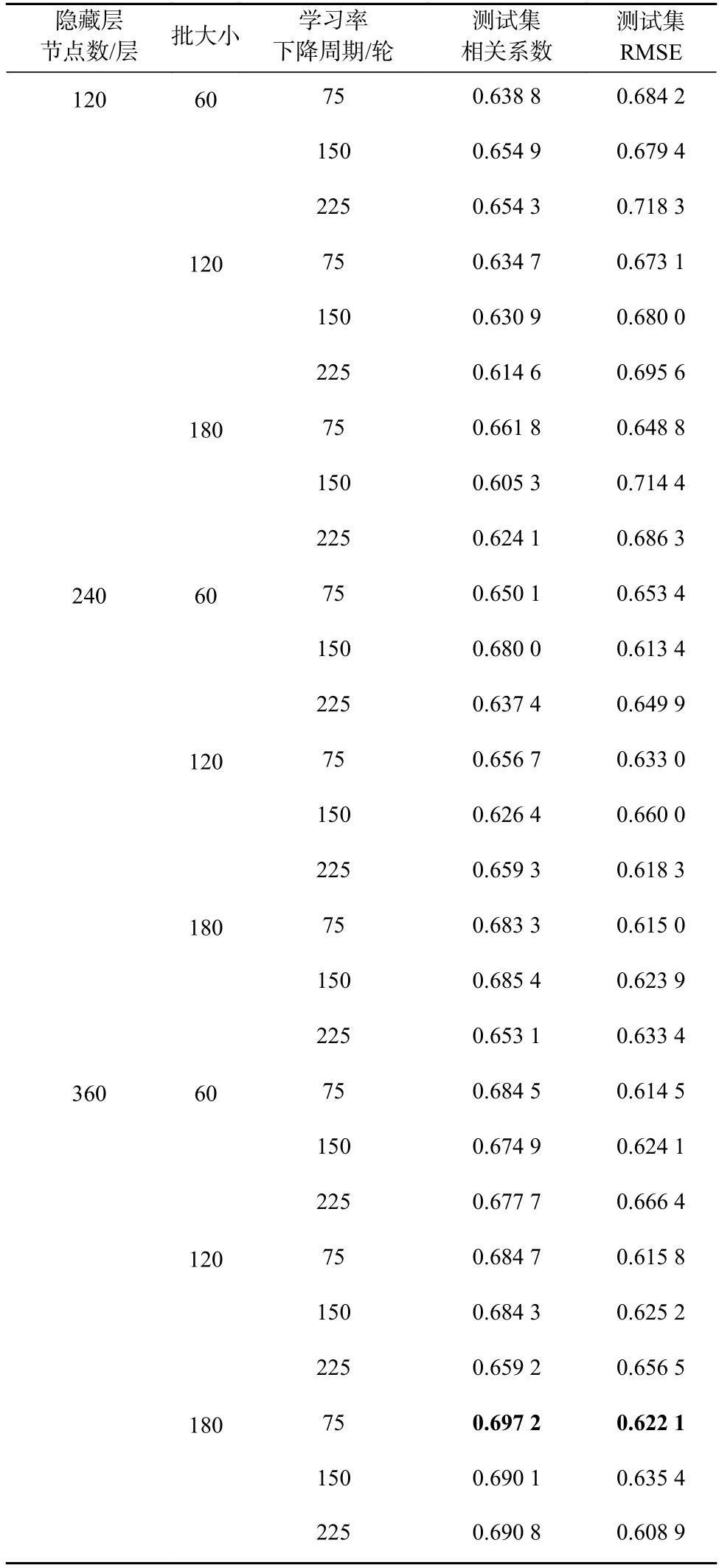
表1 交叉验证平均结果Table 1 Cross-validation average result

图6 为根据最优参数建立的LSTM 模型10 次训练的平均拟合及预测结果。1921-2010 年为模型训练集拟合结果，2011-2020 年为模型测试集的拟合结果。黑色曲线代表NOAA 提供的PDO 指数观测值；红色曲线代表多变量LSTM 神经网络模型训练结果（预测值）。PDO 指数预测值与观测值的变化趋势基本一致，在峰值和谷值处的差距较大。2013-2019 年的预测值比观测值偏小，其余时间的预测值比观测值偏大，总体来看，LSTM 神经网络模型的拟合效果比较理想；蓝色曲线代表LSTM 神经网络模型对未来10 年（2021-2030 年）的低频PDO 指数预测结果。预测结果显示，PDO 未来10 年将一直处于冷位相，北太平洋中部出现SST 正异常，热带中东太平洋和北美沿岸出现SST 负异常，PDO 指数出现两次波动，于2025 年出现最小值。

图6 LSTM 网络模型预测值及观测值Fig.6 LSTM neural network model prediction results and true values

如图7 所示，本文对比了不同模型对2011-2020 年PDO 指数的预测结果，包括单一变量LSTM 神经网络模型，统计回归模型以及多变量支持向量回归（Support Vector Regression，SVR）模型。其中，单变量LSTM 神经网络模型是由PDO 指数原始时间序列（来自NOAA）构建，经过与多变量LSTM 神经网络模型相同的交叉验证方法确定模型最优参数组合，并训练10 次取平均作为最终结果；统计回归模型采用多元回归，与多变量LSTM 神经网络模型采用相同的预报因子作为变量；多变量SVR 模型变量的选取与本文采用的多变量LSTM 神经网络模型相同。结果显示，多变量LSTM 神经网络模型拟合效果优于其他模型，特别是在峰值和谷值处更接近实际值。图8 为不同模型的误差精度评估结果，多变量LSTM 神经网络模型RMSE=0.358 0，MAE=0.298 4，MAPE=0.406 9；用PDO 指数原始时间序列构建的单变量LSTM 神经网络模型RMSE=0.447 2，MAE=0.342 4，MAPE=0.529 1；统计回归模型RMSE=0.466 1，MAE=0.409 9，MAPE=0.590 1；多变量SVR 模型RMSE=0.484 1，MAE=0.424 2，MAPE=0.629 9。从对比结果可以看出多变量LSTM 神经网络模型预测效果最好，误差最小，与实际值拟合效果最好，其次是单变量LSTM 神经网络模型、统计回归模型、多变量SVR 模型。

图7 2011-2020 年不同模型的预测结果Fig.7 Forecast results of different models from 2011 to 2020

图8 不同模型预测的精度评估结果Fig.8 Accuracy evaluation results of different model predictions

6 结论

利用1921-2020 年的海平面气压、海平面高度、热含量数据以及海冰密集度作为PDO 指数的预报要素，通过空间相关性分析选取PDO 指数预报因子，进一步将预报因子的时间序列数据进行5 年低通滤波处理，通过交叉验证选取最优参数组合，建立关于PDO 指数预测的多变量LSTM 神经网络模型，对比分析不同模型2011-2021 年的PDO 指数预测结果，进而利用模型实现了对2021-2030 年的PDO 指数的预测。通过此次研究，本文得到如下结论。

（1）基于多个预报因子数据建立的多变量LSTM神经网络模型可以有效地实现对PDO 指数的预测，模型经过交叉验证后平均相关系数和均方根误差分别为0.70 和0.62，预测结果较为理想。

（2）多变量LSTM 神经网络模型预测效果要优于多变量SVR 模型、统计回归模型以及单变量LSTM神经网络模型，其PDO 指数预测结果误差小、拟合效果好，可以作为一种新型的预测PDO 指数的手段。

（3）本文预测了未来10 年的低频PDO 指数结果，结果显示，PDO 未来10 年将一直处于冷位相，北太平洋中部将出现SST 正异常，热带中东太平洋和北美沿岸出现SST 负异常，PDO 指数出现两次波动，于2025年出现最小值。

PDO 作为年代际气候变化信号，本文建立的多变量的LSTM 人工神经网络模型实现了PDO 指数的位相预测。前人的研究[19]虽然能够有效向后预报1975-2009 年的PDO 指数（相关系数为0.81），但是其算法并不能实现对未来年代际时间尺度上PDO 指数的预报。本研究优势在于采用机器学习方法，采用更大空间范围的预报因子，一定程度上克服了预测结果对PDO 的依赖，实现了对未来10 年PDO 指数的预报。然而本研究的交叉验证试验结果与实测值相关系数在0.6～0.7 之间，低于Huang 和Wang[19]预测的相关性，产生这种结果的原因可能是其预测对象为PDO 冬季（12 月、1 月、2 月）数据，而本研究选取所有月份的数据；其次，超参数的选取具有一定主观性，在今后的研究中可以适当增加参数组合的数量来减小这种误差；最后，长时间尺度理想的预测结果要求模型用更长时间的训练集，在更长时间尺度上的预测精度有待提高。