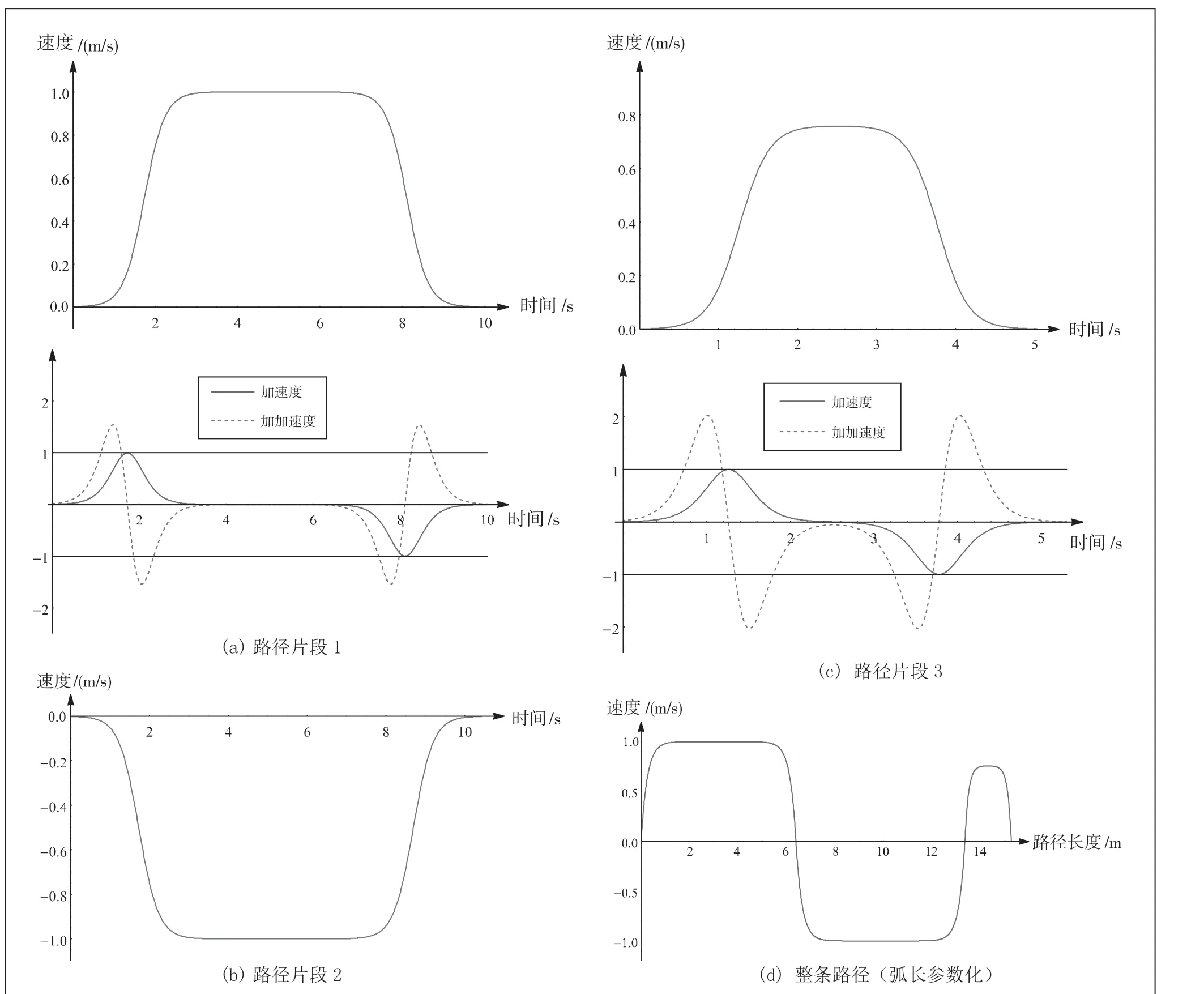
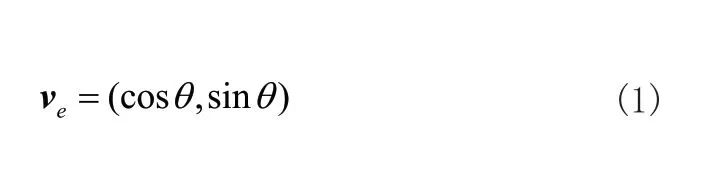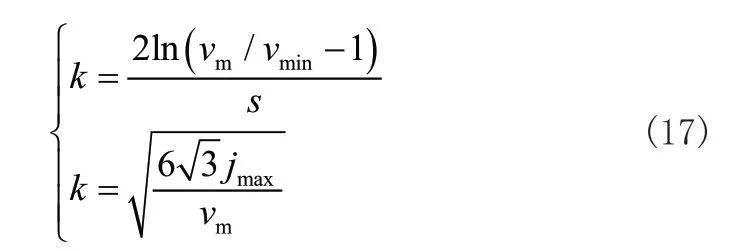无人车位姿调节轨迹规划方法

胡亚南，明瑞浩，韩国庆，刘国辉，张斌，曹子建，于洋，陆飞宇

（江苏金陵智造研究院有限公司，江苏南京，210006）

0 前言

实时轨迹规划是无人车在实际场景中大规模应用的关键技术，轨迹规划能力也成为无人车智能化程度的重要标志。对于工业和园区物流等场景，无人车在执行运输作业的过程中经常会遇到站点停靠、自动充电、临时避让等需要改变自身位置或姿态的任务。这要求无人车具有灵活的位姿调节能力，能够根据具体的任务规划一条连接起始位姿和目标位姿的可行轨迹。对于采用阿克曼转向机构的无人车，由于自身存在运动约束，通常采用Dubins 曲线、Reeds-Shepp 曲线、多项式曲线或者在离散点以及样条曲线的基础上优化得到可行的路径，然后采用梯形或S 形曲线进行速度规划。Dubins 曲线和Reeds-Shepp 曲线由于具有距离最短、易于构造的优点经常被使用。但是该类最优曲线具有bang-bang 控制的特点，其由若干段最小转向半径的圆弧和直线段拼接组成。圆弧的曲率为非零值，直线段的曲率为零，因此Reeds-Shepp 曲线在圆弧与圆弧之间以及圆弧与直线段之间的曲率是突变的。该类曲线只能保证切线连续，曲率并不连续，给无人车实际跟踪造成了困难。传统的速度规划方法需要根据输入和约束条件划分为几种情况，然后分别构造速度函数，难以保证高阶导数光滑而且计算较复杂。提出无障碍物环境中的无人车轨迹规划方法，用于在任意两个位姿之间生成满足无人车运动约束的可行轨迹，来解决路径曲率不连续、速度不光滑和计算复杂的问题。

1 路径规划

路径规划采用改进的Reeds-Shepp 曲线构造曲率连续、有界且距离最优的路径。速度规划阶段将路径分为前进和倒车片段，分别针对每个片段的长度和运动方向生成速度各阶导数光滑有界的速度轮廓。最后，将速度分配到所有路径点上得到参考轨迹。改进的Reeds-Shepp 曲线由圆弧、直线段和回旋曲线组成。其中，圆弧的半径为无人车的最小转向半径，回旋曲线用于连接两段圆弧或者直线段与圆弧，实现曲率的连续过渡。然后通过遍历各种组合方式找到距离最短的最优参考路径。

根据无人车的速度和改进的Reeds-Shepp 曲线上的起点、终点和转折点组成的点对将路径点分为前进路径片段和倒车路径片段。在位于两个点对中间的路径点上，如果无人车的期望速度为正，将两个点对之间的路径点归类为前进路径片段；在位于两个点对中间的路径点上，如果无人车的期望速度为负，将两个点对之间的路径点归类为倒车路径片段。

2 速度规划

速度规划利用指数函数光滑的性质构造速度曲线，采用的指数函数具体形式如下

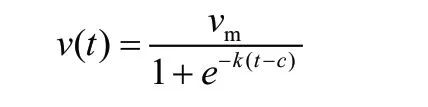
该函数以时间t 为自变量，其中，控制参数vm、k 和c 均为常数。vm是函数的极限值，对应最大速度；k 反应函数曲线的倾斜程度，决定最大加速度；c 对应速度达到最大加速度所需的时间。

速度轮廓包括上升阶段和下降阶段，两个阶段都采用权利要求4 中给出的指数函数的形式，而且参数k 取值相同，上升阶段vm>0，下降阶段vm<0。根据姿态调节时对无人车驱动系统的约束条件确定控制参数的可行范围，具体方法如下：

步骤1，根据开始时刻的速度v(0)=vm/(1+ekc)和无人车能够响应的最小速度vmin，通过关系v(0)=vmin确定参数k 和c 的关系(kc)=ln(vm/vmin-1)。

根据路径规划生成的路径片段长度和以上参数关系确定参数值，具体方法如下：

步骤3，选择参数vm=vd、k=km和c=(kc)/k 计算速度上升阶段经历的距离L=cvd=ln(vm/vmin-1)vd/km。

步骤4，比较路径片段的长度s 和速度上升阶段经历的距离L，如果s/2 ≥L，选择参数vm=vd、k=km和c=(kc)/k 得到起始段的速度函数，结束段的速度函数达到最大加速度的参数c2计算方法是c2=2(s/2-L)/vd+3c；如果s/2

3 实例分析

无人车的后轮提供驱动力，不能转向；前轮用于转向，不提供驱动力。前轮具有最大转角限制，因此无人车存在最小转向半径，记为r。选择无人车后轮驱动轴中心作为参考点，无人车的状态向量定义为Q=(x,y,θ,v)。其中，(x,y)是参考点在全局坐标系中的坐标，θ 是无人车与全局坐标系x 轴的夹角，角度规定逆时针为正方向，v 是无人车的驱动速度。

在路径规划阶段，使用改进的Reeds-Shepp 曲线生成无人车的路径。改进的Reeds-Shepp 曲线由半径为r 的圆弧、与圆弧相切的直线段和回旋曲线构成。圆弧与圆弧以及圆弧与直线段之间不是直接连接，而是通过回旋曲线过渡。回旋曲线的曲率连续变化，导致最终的路径曲率也是连续的。输入无人车出发点的状态向量QS和目标点的状态向量QT，改进的Reeds-Shepp 曲线输出连接两个状态的最短路径。最短路径以圆弧方程、直线方程和回旋曲线方程的解析形式给出。在给定离散时间间隔dt 时，带入路径的解析方程可以得到离散的路径点，每个路径点是表示无人车位姿(x,y,θ)的三维坐标。

图1 为路径规划结果。无人车的最小转向半径是r=3.5m，对应最大的曲率是κmax=1/r=0.286。无人车的出发状态是QS=(2,1,0,0)，目标状态是QT=(8,2,π,0)。完整的路径由三段路径片段组成，路径片段1 对应前进状态，路径片段2 对应倒车状态，路径片段3 对应前进状态。图2 为本发明实施例中生成的路径曲率。从图中可知曲率连续变化，并且始终位于(-κmax,κmax)范围之内。

图1 规划出的路径

图2 路径上的曲率

根据路径上无人车姿态与运动方向对路径进行分割，分割方法如下。步骤1，计算无人车的车头指向的方向向量ve，公式如下

如果两个向量的夹角α<π/2，说明无人车的朝向与路径延伸的方向相同，此时无人车的速度应为正，如果两个向量的夹角α ≥π/2，说明无人车的朝向与路径延伸的方向相反，此时无人车的速度应为负。将连续且速度相同的路径点标记为同一条路径片段。通过这种方式将整条轨迹分割成若干条路径片段。

速度规划利用指数函数光滑的性质构造速度曲线，采用的指数函数具体形式如下

式表示的速度函数以时间t 为自变量，时间t ≥0。式中，e 是自然指数，常数vm、k 和c 为控制参数，通过调节控制参数的值可以改变函数曲线的形状。控制参数的含义如下：vm是函数的极限值，对应无人车的最大速度；k 反应函数曲线的倾斜程度，决定最大加速度；c 对应速度达到最大加速度所需的时间。

一段路径片段上，无人车的速度不改变方向，假设开始和结束时刻无人车的速度均为零。此时无人车的速度轮廓包含上升阶段和下降阶段，两个阶段由两个式表示的速度函数组合得到，而且两个函数参数k 取值相同，区别在于参数c 不同，具体形式如下

步骤4，根据步骤2 和步骤3，确定同时满足两个约束时参数k 的可行范围：k ≤km，其中

步骤4，比较路径片段的长度s 和速度上升阶段经历的距离L，如果s/2 ≥L，选择参数vm=vd、k=km和c1=(kc)/k 生成上升阶段的速度函数，下降阶段的速度函数达到最大加速度的参数c2计算方法是c2=2(s/2-L)/vd+3c1；如果s/2

优选地，步骤4 中，如果s/2

图3 路径上的速度轮廓

图3 为生成的速度轮廓。其中，无人车驱动系统的参数如下：期望行驶速度为vd=1m/s，最大允许加速度为amax=1m/s2，最大允许加加速度为jmax=4m/s3，最小响应速度为vmin=0.001m/s。三段路径片段的长度分别为6.386m、6.967m、1.91m。计算得到的路径片段1 的速度函数控制参数为vm=1m/s，k=4，c1=1.727，c2=8.113；路径片段2 的速度函数控制参数为vm=-1m/s，k=4，c1=1.727，c2=8.694；路径片段3 的速度函数控制参数为vm=0.759m/s，k=5.269，c1=1.258，c2=3.775；

图4 为路径片段3 对应的参数可行范围和最优的参数值。