城市轨道交通车辆段或停车场线路用减振扣件刚度参数研究*

孙建树 和振兴 石广田 包能能 张小安

(兰州交通大学机电工程学院， 730070， 兰州∥第一作者， 硕士研究生)

车辆段或停车场(以下简称“场段”)结合上盖物业开发是城市轨道交通综合建设的趋势。为了降低或消除列车出入场段时引起的振动、噪声对上盖物业的影响，不同类型的减振降噪措施在城市轨道交通场段内得以广泛采用[1-2]，这其中也包括了造价较低、便于更换的扣件类减振措施。

文献[3-4]通过有限元方式建立车辆-轨道系统动力分析模型后发现，合理降低扣件刚度可以减小轮轨动力冲击，提高减振效果。文献[5]借助通用大型有限元动力学分析软件ANSYS/LS-DYNA，建立了车辆-线路垂向全车耦合模型，分析了车辆、钢轨的动力特性，研究了在不同的列车行车速度下城际铁路线路扣件刚度的合理取值。文献[6]通过将轨道系统简化为离散支撑的欧拉梁，分析了扣件刚度对轨道振动位移和加速度响应的影响。文献[7]采用三维车辆-轨道耦合动力学计算模型，研究了减振扣件与弹性道床垫组合下减振轨道关键动力学参数变化对车辆系统、轨道系统动力学性能及减振性能的影响规律。但是，上述研究都是在正线80 km/h及以上行车速度下进行的。

目前城市轨道交通场段内减振扣件的刚度均基于正线80 km/h及以上行车速度进行设计，而列车在场段内的行车速度一般不超过30 km/h,远低于在正线上的行车速度。根据工程经验，在列车运行速度较低的情况下，减振轨道可以采用较低的刚度，但目前缺乏此方面相关的理论研究。因此，本文在考虑车辆系统和轨道系统综合作用及相互影响的基础上，通过建立三维车辆-轨道耦合动力学仿真模型，得出车辆系统和轨道系统随减振扣件刚度变化的规律，以及城市轨道交通场段用减振扣件刚度的合理取值范围。

1 构建三维车辆-轨道耦合动力学仿真模型

本文基于车辆-轨道耦合动力学理论，建立了三维车辆-轨道耦合动力学仿真模型[8]，用以研究减振扣件刚度的合理取值范围。该模型包括车辆子系统模型、轨道子系统模型及轮轨动态耦合关系。综合考虑车辆参数、非线性轮轨蠕滑和轨道参数等因素，将模型进行求解后，可得到车辆系统和轨道系统随减振扣件刚度变化的规律。

1.1 车辆子系统模型

在车辆子系统模型中，转向架中央悬挂装置提供垂向、横向和纵向3个方向的刚度和阻尼，横向减振器、垂向减振器及抗蛇行减振器提供阻尼；轴箱悬挂装置提供3个方向的刚度，轴箱定位装置提供水平刚度，一系垂向减振器提供一系垂向阻尼。将车辆模型中每节车的车体(1个)、构架(2个)、轮对(4个)均视为刚体，每个刚体均具有横移、沉浮、侧滚、摇头、点头等5个方向的自由度，因此，整个车辆子系统共有35个自由度[8]。

1.2 轨道子系统模型

减振轨道主要包括钢轨、减振扣件、轨道基础等。轨道子系统模型中，将左右两股钢轨均视为连续弹性离散点支撑基础上的无限长Euler梁，具有垂向、横向及扭转运动3个自由度;减振扣件在垂向和横向两个方向上均采用线性节点弹簧和黏性阻尼表示;为了反映轨道基础的弹性，获得通过减振扣件传给轨道基础的振动加速度，本文将轨道基础考虑为质量弹簧阻尼系统。轨道子系统模型如图1所示。

图1 轨道子系统模型示意图Fig.1 Schematic diagram of orbital subsystem model

1.3 轮轨动态耦合关系

轮轨动态耦合关系是车辆子系统和轨道子系统之间连接的纽带，两个子系统之间的动态耦合和反馈作用都是通过这一环节实现的。轮轨动态耦合关系考虑了钢轨弹性变形对轮轨接触几何关系和轮轨动作用力的影响。轮轨的几何计算可采用迹线法。轮轨间的法向力可采用著名的赫兹非线性弹性接触理论，其计算式为：

(1)

式中：

G——轮轨接触常数；

δZ(t)——轮轨间的弹性压缩量。

轮轨间的蠕滑力先按Kalker线性理论进行计算。考虑到在列车运行过程中轮轨间的蠕滑有可能达到饱和，所以采用Shen-Hedrick-Elkins理论进行非线性修正。

2 模型的计算参数及动力学响应

动力学模型选用地铁A型车的动力学参数，只考虑列车自重，具体参数取值参照文献[9]。一般情况下，列车正线上的最大运行速度为80 km/h、车场线上的最大运行速度不超过30 km/h，故选取80 km/h和30 km/h两种速度工况来进行模型计算。轨道子系统模型中，钢轨型号选用50 kg/m，其具体参数如表1所示。

表1 轨道子系统模型的参数取值Tab.1 Orbital subsystem model parameters values

目前减振扣件的垂向刚度一般为15 kN/mm。为了研究场段内列车以不超过30 km/h的速度运行时减振扣件垂向刚度的合理取值，在本模型的计算中，减振扣件垂向刚度的取值范围为4～15 kN/mm，阻尼取7.5×104Ns/m。

由于目前对城市轨道交通的轨道不平顺谱尚处于研究阶段，本文参考文献[9]，选择属于中低速轨道不平顺谱的美国六级轨道不平顺谱作为轨道随机不平顺激扰。选取轮轨垂向力、轮轨横向力、车体垂向加速度、轨道动态变形、轨道结构振动作为车辆和轨道系统的动力学响应评价指标。图2为基于上述动力学模型、列车以80 m/h的速度通过减振轨道(减振扣件垂向刚度为15 kN/mm，阻尼为7.5×104Ns/m)时，在美国六级轨道不平顺谱激励下的动力学响应，分别为轮轨垂向力、轮轨横向力、钢轨垂向位移、钢轨垂向振动加速度、车体垂向振动加速度、轨道基础垂向加速度的响应曲线。图2中各动力学指标的响应峰值均满足标准和规定[10-11]的要求。

a) 轮轨垂向力

3 减振扣件刚度对车辆、轨道系统的影响

为了研究车场线减振扣件垂向刚度在 4～15 kN/mm范围内变化时对车辆系统、轨道系统的影响，本文对80 km/h(正线区段)和30 km/h(车场线区段)两种速度工况下、减振扣件垂向刚度在4～15 kN/mm范围内变化时车辆和轨道系统的动力学响应进行对比分析。考虑到列车在车场线上均为空车运行，列车质量按自重考虑。

3.1 减振扣件刚度对轮轨接触力的影响

列车在车场线上空车运行时，车辆系统和轨道系统受轨道随机不平顺激扰。图3对比了80 km/h和30 km/h两种速度工况下轮轨接触力随减振扣件刚度的变化趋势。

图3表明：在80 km/h和30 km/h两种速度工况下，随着减振扣件刚度的降低，轮轨横向力和垂向力均呈下降趋势；30 km/h工况下的轮轨横向力和轮轨垂向力远低于80 km/h工况下的轮轨横向力和轮轨垂向力。当减振扣件垂向刚度为4 kN/mm时，30 km/h工况下的轮轨横向力和轮轨垂向力较80 km/h工况下分别减小了47.9%和5.05%，这说明了列车在车场线上运行时轮轨间的冲击作用不大，提高轨道扣件的弹性有利于进一步降低轮轨间的冲击力。

a) 轮轨垂向力随扣件刚度的变化趋势

3.2 减振扣件刚度对车辆系统的影响

车体振动加速度是评估车辆系统动力学响应最重要的指标。对80 km/h和30 km/h两种速度工况下、减振扣件垂向刚度在4～15 kN/mm范围内变化时车体垂向振动加速度的变化趋势进行对比，结果如图4所示。

图4 车体垂向振动加速度随扣件刚度变化趋势对比Fig.4 Comparison of the trend of vehicle body vertical vibration acceleration changing with fastener stiffness

图4中，当列车分别以80 km/h和30 km/h的速度运行在减振轨道上时，减振扣件垂向刚度从15 kN/mm降低到4 kN/mm后，车体垂向振动加速度分别减小了0.005 0g和0.004 9g，变化幅度不大；80 km/h工况下的车体垂向振动加速度远大于30 km/h工况下的车体垂向振动加速度。当减振扣件垂向刚度降低到4 kN/mm时，30 km/h工况下对应的车体垂向振动加速度较80 km/h工况下对应的车体垂向振动加速度降低了52%。这表明了减振扣件刚度的降低对车辆系统影响不大，车辆系统受列车运行速度影响较大。

3.3 减振扣件刚度对轨道系统的影响

过大的钢轨垂向变形将增大线路的几何不平顺，增加轮轨之间的磨耗，甚至会导致列车脱轨掉道，因此有必要限制钢轨的垂向变形。线路不平顺会使列车在运行过程中产生一定程度的冲击，而这种冲击作用在轨道上时钢轨产生的振动非常明显，因此，钢轨振动加速度是钢轨受冲击作用时对轨道结构振动响应的综合反应，可用于评价轨道的振动特性。此外，列车运行产生的冲击作用会向下传递，引起轨下部分产生振动。图5是80 km/h和30 km/h两种速度工况下轨道系统关键动力学指标随扣件刚度的变化情况。图6为车场线用减振扣件时的轨道系统动力学响应时域对比情况。

由图5 a)中，随着减振扣件刚度的减小，两种速度工况下的钢轨垂向位移均呈现增大趋势，且钢轨垂向位移的增大以指数形式予以增长；30 km/h工况下的钢轨垂向位移略小于80 km/h的工况下的钢轨垂向位移，这说明钢轨垂向位移受列车运行速度的影响不大。在减振扣件垂向刚度为4 kN/mm时，钢轨垂向位移接近4 mm，其在30 km/h工况下的时域对比如图6 a)所示。根据CJJ/T 191—2012《浮置板轨道技术规范》[11]中“钢轨的最大垂向位移不应大于 4 mm，轨道基础的最大垂向位移不应大于 3 mm”的规定，车场线路内减振扣件的垂向刚度取值应不低于4 kN/mm。

a) 钢轨垂向位移随扣件刚度的变化趋势

由图5 b)可看出，随着减振扣件刚度的降低，两种速度工况下的钢轨垂向振动加速度均呈上升趋势；30 km/h工况下的钢轨加速度较80 km/h工况下的钢轨加速度降低了45%，且在30 km/h工况下、减振扣件垂向刚度为4 kN/mm时的钢轨垂向振动加速度远低于80 km/h工况下、减振扣件垂向刚度为15 kN/mm时的钢轨垂向振动加速度。

由图5 c)表明： 30 km/h工况下轨道基础垂向振动加速度远小于80 km/h工况下的轨道基础垂向振动加速度。当垂向刚度降低到4 kN/mm时，30 km/h工况下轨道基础垂向振动加速度较80 km/h工况下轨道基础垂向振动加速度减小了61.3%。随着减振扣件垂向刚度的减小，两种速度工况下的轨道基础垂向振动加速度均呈下降趋势。在30 km/h工况下当减振扣件垂向刚度从15 kN/mm降至4 kN/mm时，轨道基础垂向振动加速度从0.001 68g减小至0.000 73g，其时域对比如图6 b)所示。将其转换为振动加速度级，则从84.50 dB下降至77.32 dB，降低了7.18 dB。这表明在车场线内使用更低刚度的减振扣件，可以降低车辆走行部及其基础引起的振动。该措施取得了良好的减振效果，可降低对场段上盖物业开发的不利影响。

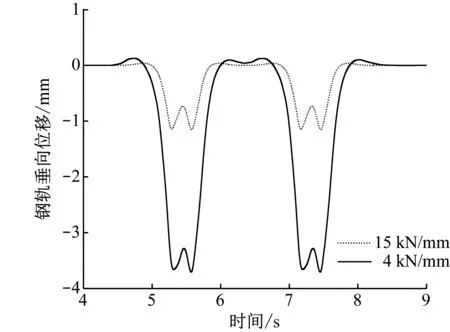
a) 钢轨垂向位移对比

4 结语

本文建立了三维车辆-轨道耦合动力学模型，研究了场段内使用更低刚度的减振扣件对车辆系统、轨道系统的动力学性能及轨道减振性能的影响规律，给出了场段用减振扣件刚度的合理取值范围。主要结论如下：

1) 相同刚度的减振扣件用于正线(列车运行速度为80 km/h)和车场线(列车运行速度为30 km/h)时，车辆系统和轨道系统的主要动力学响应指标存在显著差异。

2) 车场线减振扣件的刚度取值可以比正线更低。当减振扣件刚度由15 kN/mm降至4 kN/mm时，轮轨力、车体振动加速度、轨道基础加速度呈减小趋势，钢轨垂向位移和钢轨垂向振动加速度呈增大趋势。其中，钢轨垂向位移接近《浮置板轨道技术规范》所规定的钢轨位移上限，但车场线的钢轨垂向振动加速度小于正线。所以，车场线内减振扣件刚度的取值不宜低于4 kN/mm。

3) 降低车场线减振扣件的刚度，有利于减小传给轨下基础的振动。若减振扣件的垂向刚度从15 kN/mm降至4 kN/mm，所对应的减振效果比既有的减振扣件提高7.18 dB，减振效果较为显著。

4) 车场线减振扣件刚度对车辆系统的振动加速度影响不大，减振扣件垂向刚度从15 kN/mm降至4 kN/mm，车体振动加速度仅减小了0.004 9g。从车辆系统角度来说，降低车场线减振扣件的刚度是可行的。

5) 应根据场段内列车运行速度条件，设计、开发比正线扣件更低(不低于4 kN/mm)的减振扣件。