水力测功机瞬态特性研究
2022-07-20孟明站吴大转
孟明站,杨 帅,吴大转,郑 枫,潘 燚
(1.浙江大学 能源工程学院,杭州 310027;2.西安精密机械研究所昆明分部,昆明 650101)
0 引言
测功机作为动力装置的一种负载设备,能够进行动力装置的动力性能测试,其中水力测功机凭借结构简单,价格低廉,运行平稳可靠等优点广泛应用于大功率动力装置的动力性能测试中[1]。随着动力装置要求越来越高,动力装置启动过程中的瞬态特性成为了关注重点,因此为了更好地配合动力设备的瞬态启动过程,需要进行水力测功机的瞬态加载特性研究,从而间接了解动力设备的瞬态特性。
基于Froude 型水力测功机,RAINE 等[2-3]研究了扭矩吸收的原理,描述了稳态扭矩吸收过程的数学模型,并基于此研究了开环和闭环控制模式下的水力测功机控制系统,推动了水力测功机的研究。杜丹丰等[4]将水环在测功机内部的运动看作是圆周运动与环流运动的组合,分别计算环流运动的环流力矩和圆周运动的摩擦力矩,采用经验公式与数学分析结合的方法,得到制动扭矩随水层厚度的变化关系。姚新芳[5]利用数值模拟软件FLUENT,对不同条件下的水力测功机流场流动进行数值模拟,通过对水力测功机叶片角度和水温的参数改变,比较了不同条件下的扭矩吸收结果。TSUKAMOTO 等[6-9]通过对叶轮机械中的离心泵进行研究,认为叶轮机械的瞬态性能与稳态性能有一定差异。吴大转等[10-20]通过较多的试验和数据,证明通过变转速控制和滑移网格的数值模拟方法研究叶轮机械启动过程具有可行性。
综上所述,CFD 方法对于研究叶轮机械的瞬态启动过程具有一定参考价值,但是目前对于水力测功机瞬态启动过程的研究较少。因此,本文利用FLUENT 软件对水力测功机瞬态启动过程进行研究,重点分析瞬态启动特性和特性影响因素。
1 水力测功机数值模拟
1.1 几何模型
选取Y4800 型大功率水力测功机为研究对象,整体计算域由进水流道、定子流域、转子流域、排水流道组成。流体由进水流道流入,在工作腔内做复杂三维流动,最后沿着定转子中间流域汇集到排水流道排出。其中定转子基本结构参数见表1,使用UG 软件构建流域的三维模型如图1 所示。
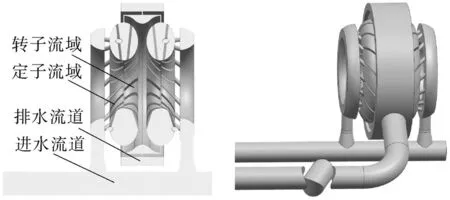
图1 水力测功机流域Fig.1 Flow domain of hydraulic dynamometer

表1 水力测功机定转子参数Tab.1 Parameters of stator and rotor of hydraulic dynamometer
1.2 网格划分
采用ICEM 软件对水力测功机计算域进行网格划分,由于整体结构比较复杂,将各个部件分别进行网格划分,最后进行组装。其中较为核心的定转子结构采用六面体网格划分,网格质量在0.6以上,最终的网格划分结果如图2 所示。

图2 水力测功机流域网格Fig.2 Mesh of flow domain of hydraulic dynamometer
1.3 边界条件和参数设置
水力测功机试验系统进水管路中设有稳压罐,能够保证入口压力的恒定,出口处连通大气,因此水力测功机流域入口采用压力入口,设置为0.1 MPa(表压),出口采用压力出口,设置为0 MPa(表压)。壁面采用增强壁面函数,湍流模型采用Realizable 模型。压力与速度的耦合算法采用SIMPLEC。对于转子的旋转运动,采用动区域计算模型中的网格滑移技术,并通过UDF 进行转子的转速控制。假定水力测功机内空腔始终充满水,采用水力测功机转子所受的扭矩作为水力测功机的吸收扭矩,对比分析水力测功机的吸功性能。
模拟中需要对网格无关性进行验证,以相同比率改变模型网格的尺寸,获得5 组网格类型,通过对转速为400 r/min 时的数值模拟结果进行比较,获得的扭矩和流量结果如图3 所示。
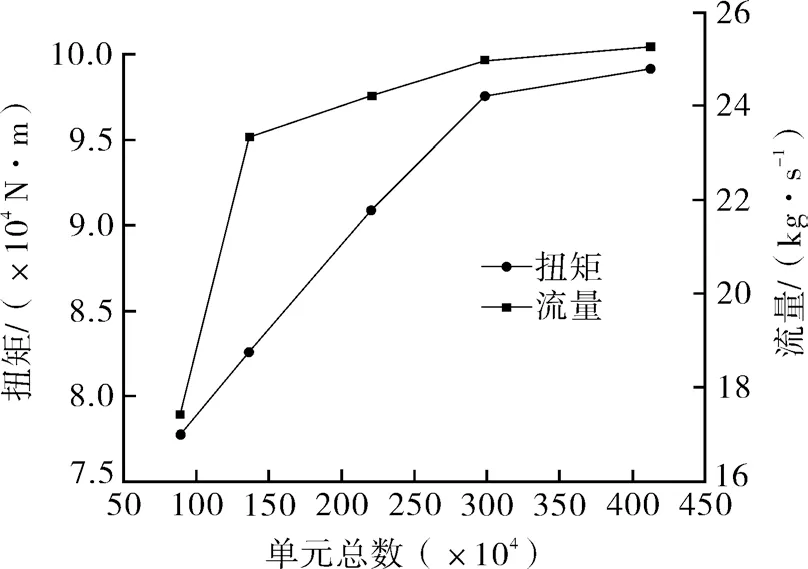
图3 网格无关性Fig.3 Grid independence
考虑到模拟的精度和计算资源的消耗,最终确定网格单元数为298.3 万。同时在瞬态模拟中考虑到时间步步长对瞬态结果的影响,时间步长过大,导致计算结果比较粗糙,会忽略瞬态过程中流体的加速过程;时间步长过小,又会增加计算时间步,浪费计算资源。兼顾计算精度和计算能力,决定采用计算的时间步步长为0.000 667 s。
2 结果讨论与分析
2.1 瞬态启动性能对比分析
设定水力测功机瞬态启动的转速加载方式为线性加载,前0.5 s 是瞬态启动阶段,后0.5 s 是定转速运行阶段。转子转速随时间变化的规律如下所示:
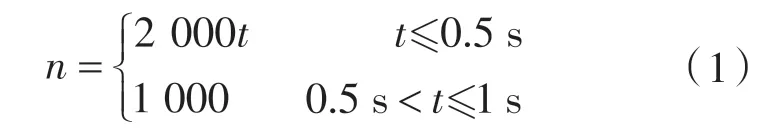
由图4(a)可知,在瞬态启动阶段,水力测功机的吸收扭矩随时间的变化而增加。t=0.5 s 时,转子转速达到最大值1 000 r/min,此时水力测功机的吸收扭矩没有达到稳定状态的最大值,约0.02 s 后,吸收扭矩达到最大值,水力测功机的吸收扭矩滞后于转速达到稳定状态。图4(b)示出在不同工况下,水力测功机吸收扭矩随转速的变化。可知,整个瞬态启动过程中,相同转速下瞬态工况的吸收扭矩始终小于稳态工况,并且在启动初期阶段,瞬态工况下的吸收扭矩远小于同转速下稳态工况的吸收扭矩。转速在0~350 r/min 时,吸收扭矩差值逐渐增大,转速在350~600 r/min时,吸收扭矩差值逐渐减小,最大为54 839 N·m,此时瞬态吸收扭矩约为稳态吸收扭矩的27.5%。当转速大于600 r/min 时,2 种运行状态下,吸收扭矩差值比例基本保持不变,相差约为7.5%。

图4 水力测功机瞬态启动结果分析Fig.4 Analysis of transient startup results of hydraulic dynamometer
水力测功机内流体在定子与转子间形成环流漩涡,这一流动形式是水力测功机吸收扭矩和功率的主要贡献来源,因此取定转子叶片中间的横截面,即环流截面如图5 所示,分析水力测功机内部的流动规律。
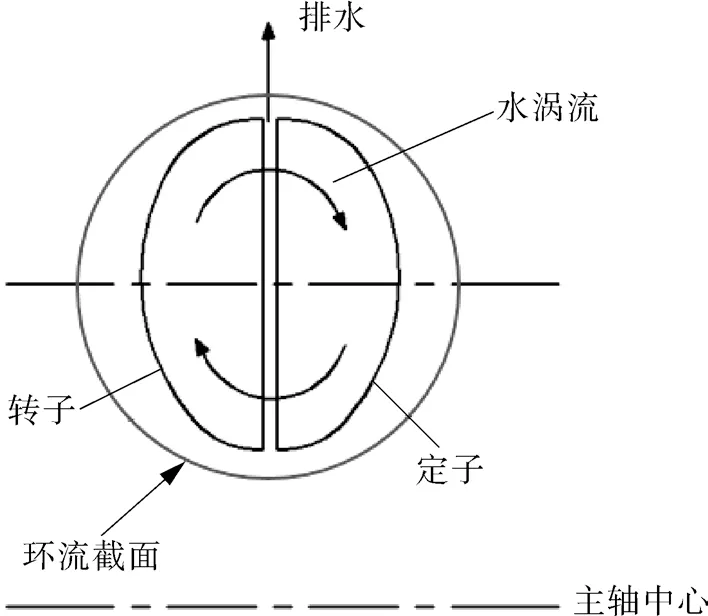
图5 水力测功机环流截面Fig.5 Circulation cross section of hydraulic dynamometer
图6 示出瞬态和稳态工况水力测功机不同转速环流截面的处速度分布。
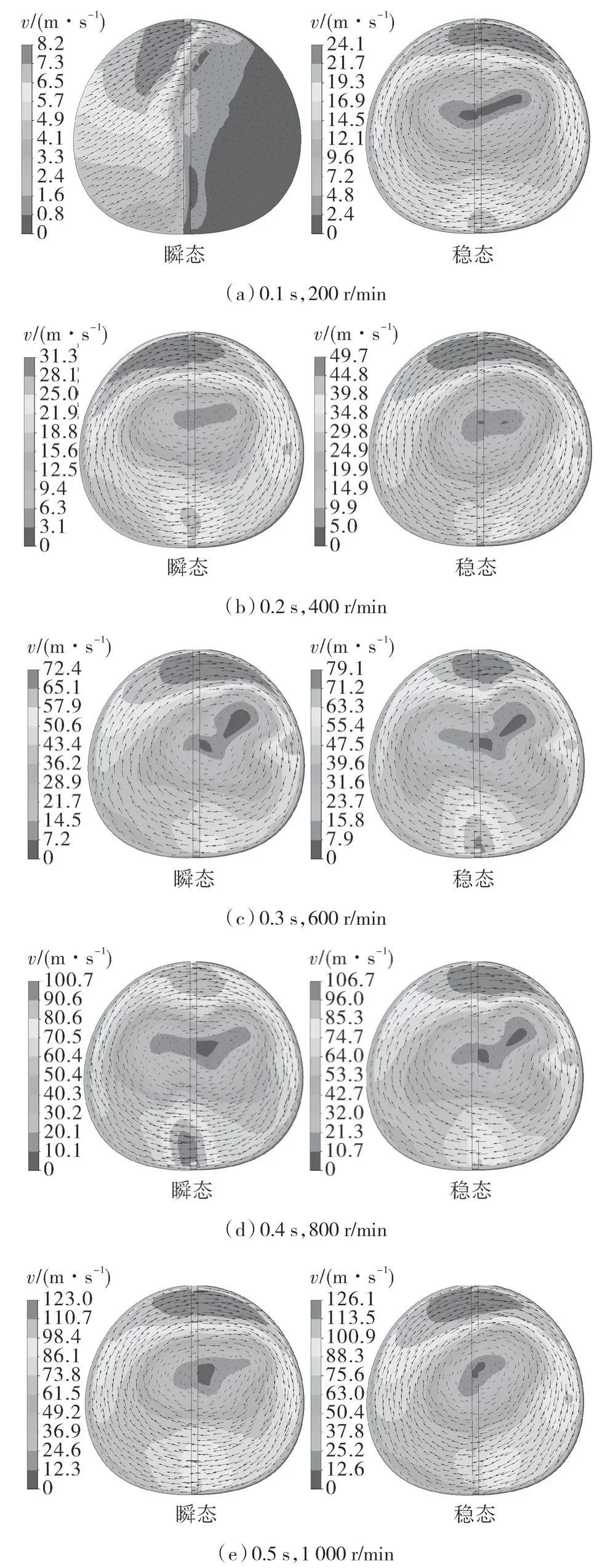
图6 不同工况下水力测功机环流截面速度分布Fig.6 Velocity distribution of circulation cross section of hydraulic dynamometer under different operating conditions
由图6 可见,瞬态启动过程中,水力测功机内流场平均流速总是小于稳态流场,随着转速的增加,两者差异在逐渐降低。因为流体的惯性作用,流体介质具有一个加速的过程,转子速度改变后一段时间流场才能达到速度改变之后的稳定状态。瞬态启动过程中,转子转速一直在增加,因此瞬态流场始终滞后于同转速下的稳态流场,瞬态工况下吸收扭矩和吸收功率也低于稳态工况。
2.2 加载方式的影响
探究加载方式对水力测功机瞬态启动特性的影响,其中转速增长规律分别为线性增长、二次曲线增长和三次曲线增长,瞬态启动过程转子具有变化的启动加速度。转子转速随时间变化的启动规律如下所示。

图7 示出不同加载方式下水力测功机吸收扭矩随转速的变化情况。

图7 不同加载方式下水力测功机吸收扭矩的变化曲线Fig.7 Variation curve of absorbed torque of hydraulic dynamometer under different loading modes
将3 种瞬态启动工况下吸收扭矩随时间的变化转化为吸收扭矩随转速的变化,能够进行相同转速条件下水力测功机吸收扭矩的对比分析。可知,3 种瞬态工况下的吸收扭矩均小于同转速下的稳态工况结果,在瞬态启动初期,瞬态工况和稳态工况吸收扭矩的差值更大。线性加载条件下的吸收扭矩大于另外两种工况的结果。在转速大于600 r/min 时,3 种加载方式下瞬态工况与稳态工况吸收扭矩的差值基本保持不变。转速为600 r/min 时,吸收扭矩差值分别为28 031,40 266和62 436 N·m,瞬态吸收扭矩约占同转速下稳态吸收扭矩的88.7%,82.3%,72.6%。
图8,9 分别示出4 种不同工况下水力测功机环流截面处的速度分布。从图中可以看出,启动初期阶段,转子转速为200 r/min 时,瞬态工况流场明显滞后于稳态工况流场。瞬态工况内环流截面处还没有形成完整的环流漩涡,流场速度较小,而稳态工况下已经形成环流漩涡,在定转子间进行流体动量和能量的交换,因此此时水力测功机的吸收扭矩远小于稳态工况;启动中后期阶段,转子转速为600 r/min 时,瞬态工况与稳态工况的流场形态基本相同,但稳态工况流场的流动速度仍大于瞬态工况。
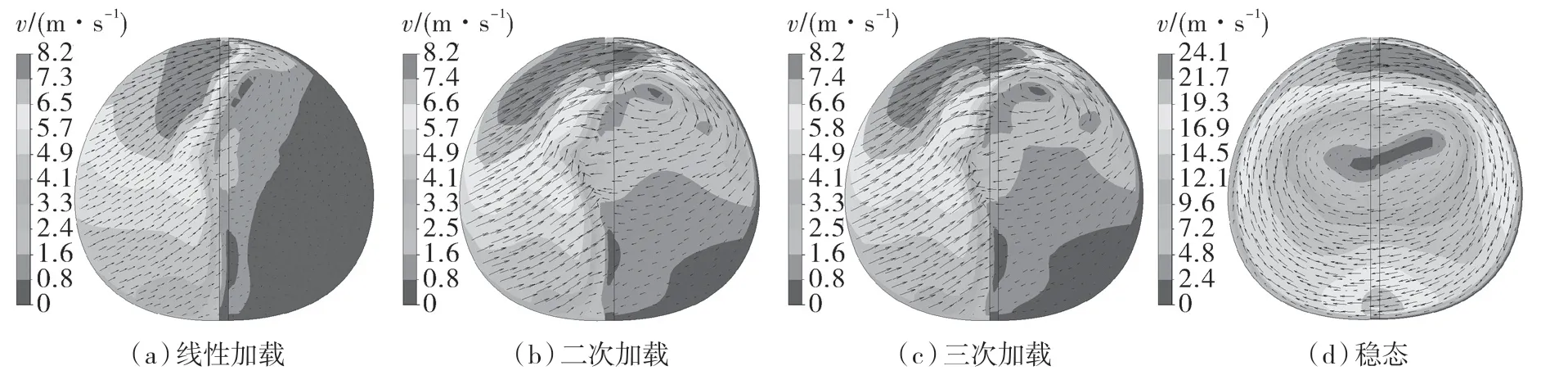
图8 转速为200 r/min 时不同加载方式下环流截面速度分布Fig.8 Circulation cross-section velocity distribution under different loading modes at 200 r/min

图9 转速为600 r/min 时不同加载方式下环流截面速度分布Fig.9 Circulation cross-section velocity distribution under different loading modes at 600 r/min
2.3 加载时间的影响
在恒定的启动加速度条件下,探究启动加速度数值的大小,即加载时间对水力测功机瞬态启动特性的影响。具体的转子转速变化规律如下所示。
加载时长t=0.5 s:
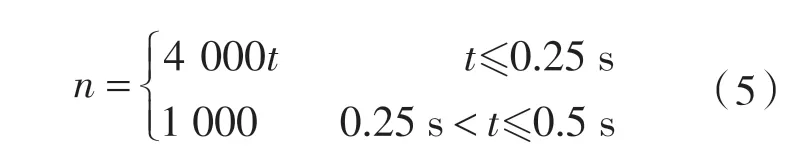
加载时长t=1 s:
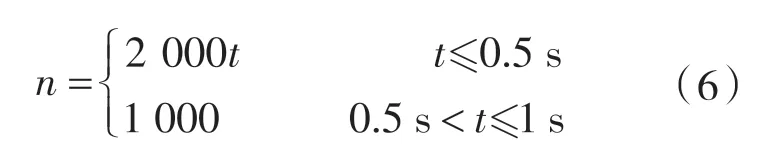
加载时间t=1.5 s:

图10 示出瞬态启动初期阶段不同加载工况下水力测功机吸收扭矩随时间的变化曲线。
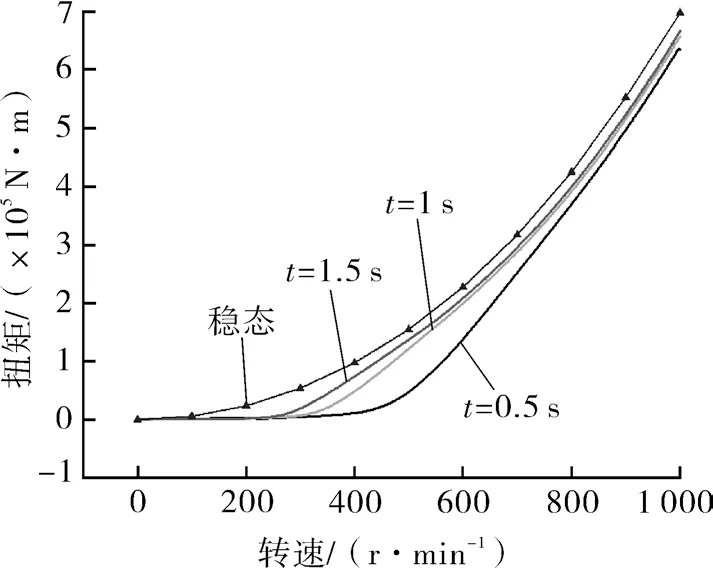
图10 不同加载时长下水力测功机的吸收扭矩Fig.10 Absorbed torque of hydraulic dynamometer under different loading times
可知加载时间越短(稳定状态下的工况可以看作加载时间无限长得到的结果),对应工况下的吸收扭矩就越小。这是因为流场滞后状态决定总吸收扭矩的大小,加载时间越短,转子叶片对流场的作用时间就越短,流场滞后效应越大,水力测功机的吸收扭矩就越小。在加载时间分别为0.5,1 和1.5 s 时,瞬态与稳态工况最大吸收扭矩差值分别为106 516,54 449 和36 203 N·m,对应的转速分别为500,336 和272 r/min,瞬态吸收扭矩约为同转速下稳态吸收扭矩的20%,22%和31%。
图11,12 分别示出4 种不同工况下水力测功机环流截面处的速度分布。可知,在启动初期阶段,转速为200 r/min 时,瞬态工况流场明显滞后于稳态流场,瞬态工况的流动形式与稳态工况的流场形态也存在很大差别,并且加载时间越长,滞后效应越小,验证了流场的滞后情况。同时在瞬态启动中后期阶段,转子转速为600 r/min 时,瞬态工况流场仍滞后于稳态流场,但与初期阶段不同,流动形态已经基本相同,并且加载时间越长,流场滞后效应越小。

图11 转速为200 r/min 时不同加载时长环流截面速度分布Fig.11 Circulation cross-section velocity distribution under different loading times at 200 r/min
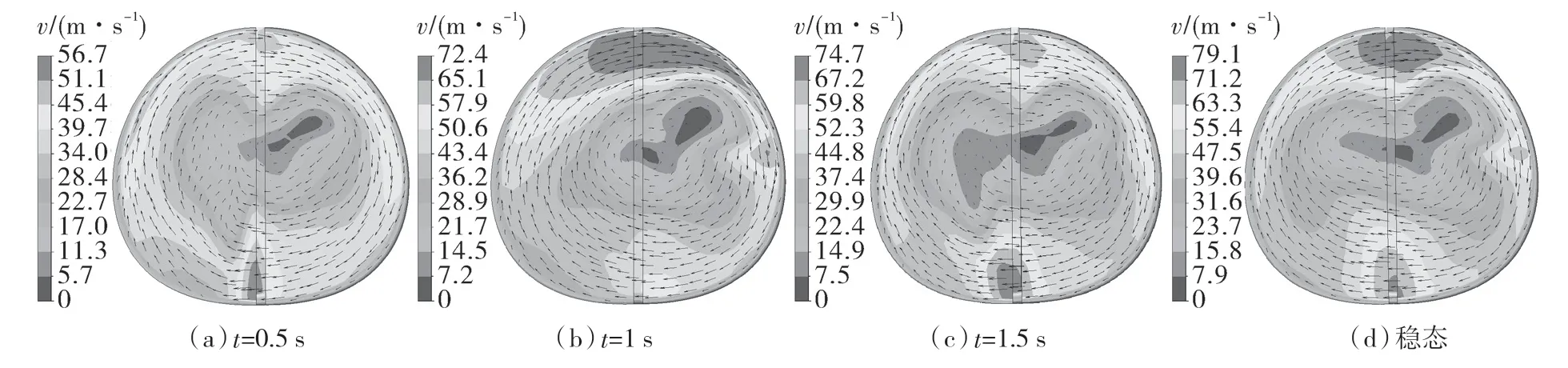
图12 转速为600 r/min 时不同加载时长环流截面速度分布Fig.12 Circulation cross-section velocity distribution under different loading times at 600 r/min
3 结论
(1)水力测功机瞬态启动过程流场相对于稳态流场存在明显的滞后效应,表现在性能曲线上是瞬态性能曲线偏离稳态性能曲线,相同转速下瞬态启动过程吸收扭矩小于稳态过程,转速在350 r/min 时两者相差最大,为54 839 N·m,此时瞬态吸收扭矩约为稳态吸收扭矩的27.5%。
(2)不同加载方式下,线性加载方式在瞬态启动过程中具有较大的吸收扭矩,并且在瞬态启动中后期阶段,瞬态工况与稳态工况的扭矩差值基本保持不变。转速为600 r/min 时,线性加载、二次加载和三次加载与稳态下吸收扭矩差值分别为28 031,40 266 和62 436 N·m,瞬态吸收扭矩约占稳态吸收扭矩的88.7%,82.3%,72.6%。
(3)不同加载时长下,加载时间越长,流场进行充分流动的时间就越长,流场滞后效应越弱,吸收扭矩越大。在加载时长分别为0.5,1 和1.5 s时,最大吸收扭矩差值分别为106 516,54 449 和36 203 N·m,此时转速分别为500,336,272 r/min,瞬态吸收扭矩约为同转速下稳态吸收扭矩的20%,22%和31%。
