轮胎残余回正力矩测试和计算方法研究

俞 旻，杨 通，张文清，俞 峰

（中策橡胶集团股份有限公司，浙江 杭州 310018）

当车辆在平整路面上直线行驶时，如果驾驶员双手离开方向盘，车辆不一定能保持直线方向继续前进，而是会逐渐出现偏斜[1]。研究这个现象需要掌握微小侧偏角时轮胎侧向力与回正力矩的关系[2-4]。回正力矩为零时的轮胎侧偏角（α1）造成的侧向力为残余侧向力，侧向力为零时的侧偏角（α2）造成的回正力矩为残余回正力矩[5-6]。

驾驶员双手离开方向盘后，前轮主销上的力矩消失，轮胎在侧偏角保持α1的状态下继续滚动，产生残余侧向力。由于路面一般倾斜，车辆右侧通行时，道路左边高右边低，为了让车辆大致保持直线前进，需要按照一定的方向贴带束层，从而使残余侧向力的方向朝向车辆行驶方向的左侧。另一方面，需要保持一个固定方向行驶时，为了避免前轮受到横向力，需要使轮胎侧偏角为α2，此时轮胎会产生残余回正力矩，需要给方向盘施加一个与残余回正力矩相抗衡的力矩。引发残余侧向力和残余回正力矩的原因有角度效应和锥度效应等[7-8]。改变轮胎旋转方向时，角度效应残余侧向力（PRLF）和角度效应残余回正力矩（PRAT）均发生在旋转方向的同一侧，锥度效应残余侧向力（CRLF）和锥度效应残余回正力矩（CRAT）均发生在旋转方向的另一侧。

PRAT主要由胎面花纹和带束层贴合方向引起，是微小侧偏角范围内的轮胎特性，也是车辆跑偏研究的重要指标。轮胎残余回正力矩试验可通过正弦、扫掠或稳态的方式在微小范围内变化侧偏角进行。PRLF和PRAT数值根据轮胎左转和右转试验工况下测得的侧向力、回正力矩关于侧偏角的曲线计算得到。目前，普遍采用美国汽车工程师学会推荐方法（简称SAE方法）和通用汽车公司推荐方法（简称GMW方法）计算PRAT，第1种先去除锥度效应，然后求残余回正力矩[9]；第2种先分别求得左转和右转工况下的残余回正力矩，然后去除锥度效应，再得到PRAT[10]。由于不同测试方法和计算方法得到的PRAT会产生差异，本工作通过3种测试方法和2种计算方法分析不同花纹轮胎的PRAT，从而为轮胎跑偏研究提供支持。

1 实验

1.1 试验轮胎

选择规格为215/55R17 94V的轿车轮胎为试验轮胎，对称花纹和非对称花纹的试验轮胎（以下简称轮胎A和轮胎B）各选2条，如图1所示。

图1 试验轮胎

1.2 试验设备

使用美国美特斯工业系统公司（MTS）的Flat-Trac CT Ⅲ轮胎力和力矩测试系统。此系统可执行侧偏角正弦、侧偏角扫掠、稳态或更复杂的自定义试验，随设备带有侧偏角正弦残余回正力矩试验与计算模板。

1.3 试验条件和方法

试验条件为：充气压力 230 kPa，负荷6 566 N，速度 80 km·h-1，侧偏角范围－1°～1°。

侧偏角正弦方法（以下简称Sin）中侧偏角呈正弦波变化，频率为0.1 Hz，数据采集频率为200 Hz；侧偏角扫掠方法（以下简称Swp）中侧偏角呈三角波变化，速率为0.4 （°）·s-1，数据采集频率为200 Hz；稳态方法（以下简称SS）中侧偏角取值分别为1°，0.7°，0.4°，0.2°，0°，－0.2°，－0.4°，－0.7°和－1°，在每个侧偏角工况下轮胎滚动2圈后，等间隔采集1圈（90个）数据点。

采用3种测试方法，均重复进行10次试验。每条轮胎Sin和Swp的总试验时间均为20 min，SS的试验时间为40 min。

2 计算方法

对测试数据进行曲线拟合，得到轮胎右转和左转工况下的侧向力（FR和FL）和回正力矩（MR和ML）关于侧偏角（α）的曲线方程，如下式所示：

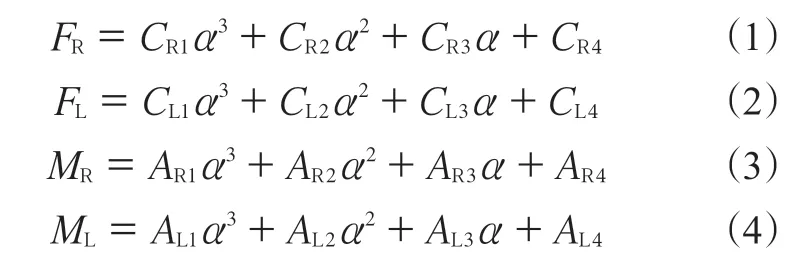
式中，CR1—CR4和CL1—CL4分别为右转和左转工况下的3次侧向力曲线拟合系数，AR1—AR4和AL1—AL4分别为右转和左转工况下的3次回正力矩曲线拟合系数。

2.1 SAE方法

SAE方法首先对式（1）和（2）、式（3）和（4）进行平均，将锥度效应去除，得到仅包含角度效应的曲线方程，如下式所示：

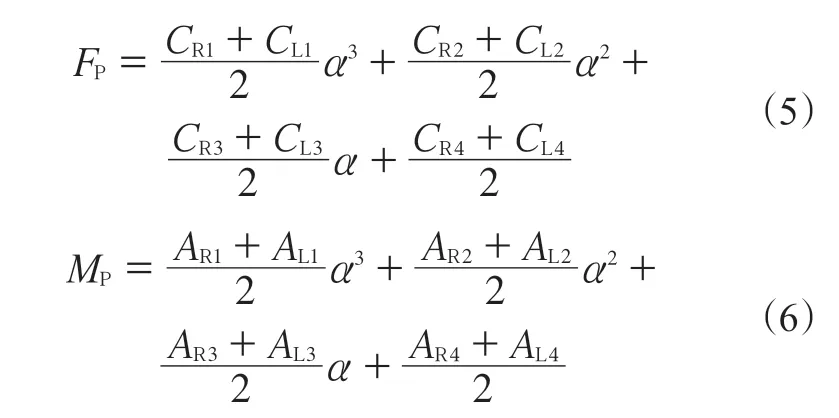
式中，FP为FR和FL的平均值，MP为MR和ML的平均值。

当式（5）中FP为零时，求得式（6）对应的MP即为PRAT。

物理教师要引导学生在课下做好零散知识的总结以及归纳，从而形成系统的知识网络体系。物理课程主要是一门实践性较强的实验课程，所以学生必须熟练掌握理论知识，同时能够在实践中运用这些理论知识。这就要求物理教师除了要做好课堂教学工作外，还要主动引导学生参与实验活动。而且，学生参加实验活动后，针对实验过程一定要记录实验感受以及实验过程，从而在更大程度上提升对物理知识的理解以及掌握。

2.2 GMW方法

GMW方法首先求得式（1）和（2）中FR和FL为零时式（3）和（4）所对应的MR和ML，分别为右转和左转工况的总残余回正力矩（TR和TL），计算其平均值（T），即为PRAT：

2种计算方法的主要区别是目的不同，SAE方法是将右转和左转工况平均处理，以整体描述PRAT特性，GMW方法则着重深入计算和考量轮胎右转和左转工况下的跑偏特性参数。

3 结果与讨论

3.1 拟合精度

采用式（8）[11]对3种测试方法得到的3次曲线拟合精度（a）进行计算，10次测试的平均拟合精度如表1所示。

表1 3种测试方法的拟合精度 %

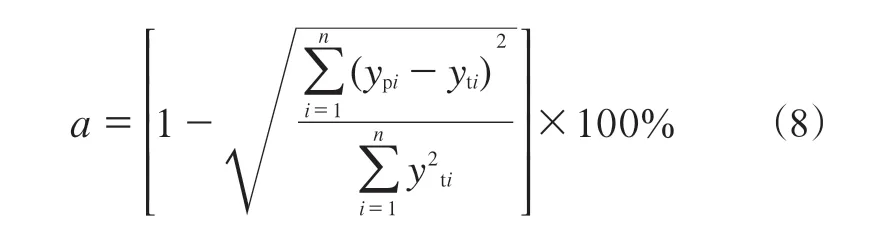
式中，ypi为曲线拟合后求得的侧向力或回正力矩，yti为实测值。

从表1可以看出，3种测试方法中SS结果的拟合精度最高，Sin和Swp的回正力矩曲线拟合精度与SS的差距相对较大。原因是SS测试时先对每个侧偏角工况下采集的原始数据进行平均处理后再拟合成曲线；Sin和Swp则是直接对原始数据进行拟合，并且是准稳态测试，拟合测试点数量远多于SS，数据波动相对较大，控制精度不及SS，如图2所示。

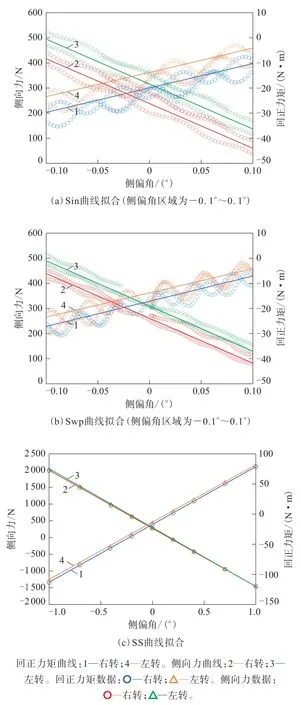
图2 轮胎B测试曲线拟合结果

3.2 结果分析

不同测试和计算方法得到的PRAT结果如表2所示。

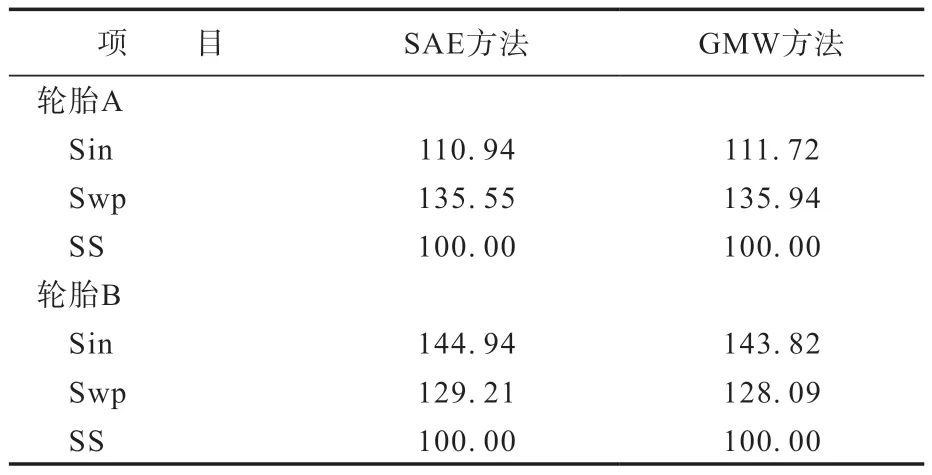
表3 PRAT相对值 %

从 表2 和3 可 以 看 出，SS 的PRAT 最 小，其他测试方法得到的PRAT为SS测试结果的110.94%～144.94%。不同测试方法得到的PRAT有一定差别，再现性（对同一条轮胎，用不同的测试方法得到的PRAT结果的差异）不高。

SS的PRAT标准差和变异系数最小，测试重复性（用相同测试方法进行多次测试，测试结果间的差异）最好。与轮胎A相比，轮胎B的Sin和Swp的PRAT变异系数相对较大。

以SAE方法计算的PRAT为基准，可求得GMW方法计算的PRAT相对偏差，如表4所示。

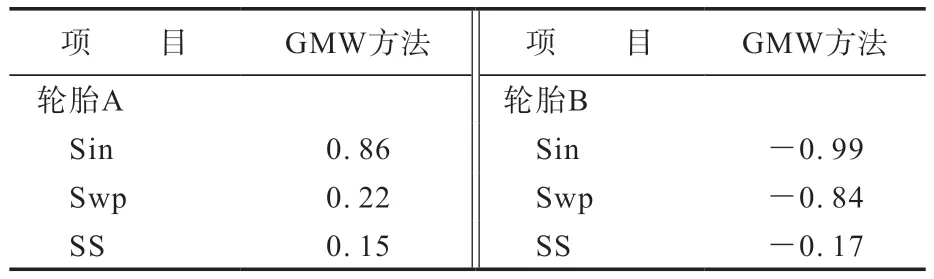
表4 PRAT测试结果相对偏差 %

从表2—4可以看出，SAE和GMW计算方法虽然定义和公式不同，但是求得的PRAT差异很小，均在1%以内。对于轮胎B，2种方法计算的PRAT差异与轮胎A无明显区别，针对轮胎B的PRAT无需特别选择其计算方法。

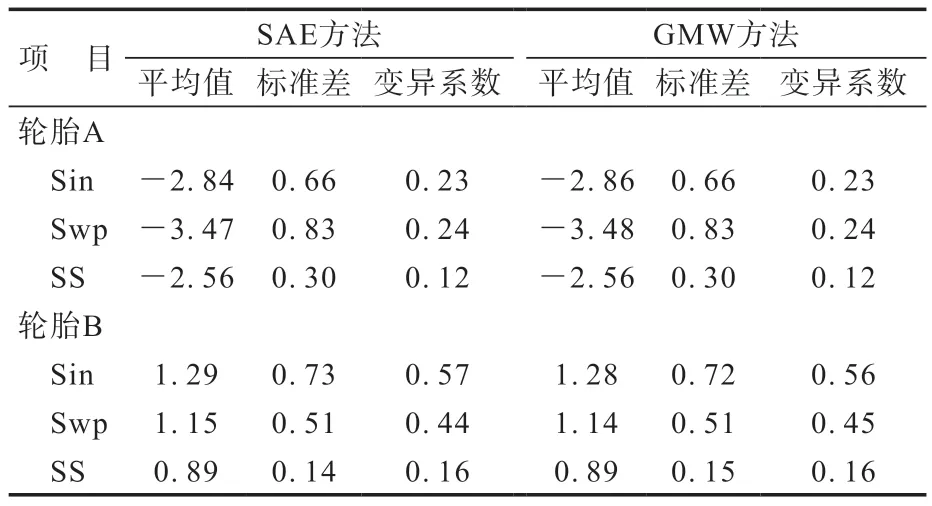
表2 PRAT计算结果 N·m

同时，3种测试方法中，SS的测试时间相对较长。

4 结论

（1）Sin和Swp的测试时间较短，能够节省一定测试成本。

（2）与Sin和Swp相比，SS的曲线拟合精度最高，测试重复性最好，非对称花纹轮胎采用Sin和Swp的重复性相对较差。不同测试方法得到的PRAT有一定差异，再现性不高。

（3）SAE和GMW两种计算方法求得的PRAT基本无差异。