基于机器学习的车辆冲撞威胁可能性评估方法研究
2022-07-20刘佳琦陈文静
刘佳琦, 陈文静
(中国人民公安大学信息网络安全学院, 北京 100038)
0 引言
当今世界恐怖主义、极端暴力袭击事件频发,给人民安全和社会稳定带来极大威胁。车辆冲撞是指袭击者以车辆作为武器故意驾驶车辆撞向建筑物、人群或者其他目标的行为。通过统计分析近15年全球恐怖主义数据库(Global Terrorism Database,GTD)所收录的恐怖主义事件,发现车辆冲撞事件数量呈现逐年上升趋势。由于国内对于爆炸物、枪支和刀具的严格管控,使得车辆成为恐怖分子和极端犯罪分子最容易获得的武器,车辆冲撞已然成为国内恐怖袭击最主要威胁之一。对恐怖活动的风险评估成为近年来国内外研究的热点问题。
风险评估流程在《风险管理原则与实施指南》(GB/T 24353—2009)中进行了明确,风险评估包括风险识别、风险分析及风险评价3个重要步骤[1]。社会安全风险评估通常将风险分析分为袭击发生可能性分析(敌手能力)、安防系统脆弱性分析及袭击发生的后果分析3个部分,其中可能性评估是风险评估的重要组成部分,是对袭击发生的可能程度进行分析与评估,其评估结果对风险评估的结果有重要的影响,通过可能性评估,能够准确分析袭击者的意图和能力,也可以在进行风险相关决策时为风险管理者提供参考依据。
随着安全风险评估技术的不断发展,威胁发生可能性评估已经有了一套较为完整的流程。首先明确针对防护目标的恶意威胁行为,收集相关数据信息、历史案件资料,再建立可能性评估指标体系,最后通过层次分析法、模糊综合评价法、ANP等评估方法得到可能性分值。辛晶等应用网络层次分析法对石油化工设施安全进行了风险评估[2]。王永宝等应用风险矩阵对风险可能性进行了分析[3]。卢耀健等基于模糊随机方法对台风灾害模糊可能性进行分析,最终得到台风灾害模糊风险评估模型[4]。王肖霞等引入广义模糊数定量描述专家信息,先利用可能性分布统一表征信息,然后利用相似测度对可能性熵权进行调整最后完成尾矿坝风险可能性评估[5]。可能性评估研究仍然存在一定局限性,首先风险评估评模型中的可能性评估指标多为历史事件、对手数量、动机等指标,指标数量较少覆盖不够全面,缺少科学和全面的可能性评估指标体系研究,同时指标分级标准不够细致精准,难以实现科学量化;其次评估方法多采用专家经验法,过分强调专家主观意愿,评估结果缺少客观性,依赖专家经验的评估方法同时存在评估结果不稳定的问题。
综上所述,恐怖袭击成因错综复杂,单纯的定性或定量分析难以科学和全面地评估袭击发生的可能性。基于此,本文提出了一种基于PSO- BP神经网络的车辆冲撞威胁可能性评估方法,首先收集2006~2020年间国内外发生的车辆冲撞案例,在案例分析基础上结合专家经验建立车辆冲撞可能性指标体系, 根据案例描述,结合专家经验建立可能性评估指标数据集,再利用神经网络对数据集进行反复学习和训练,实现可复用的车辆冲撞威胁可能性评估模型,通过实验分析,该模型可以科学、全面的对威胁发生可能性进行评估。
1 可能性评估指标体系及数据集构建
为了科学、全面地构建车辆冲撞可能性评估指标体系,用更加真实、准确的数据训练神经网络,得到科学实用的可能性评估模型,本文构建了针对车辆冲撞威胁案例集和可能性评估指标数据集。
1.1 案例收集与分析
通过收集国内外发生具有一定关注度的车辆冲撞案例,对案例进行分析研究后发现,车辆冲撞事件除以政治、宗教等问题为动机的恐怖事件外,还有很多以酗酒、吸毒、个人泄愤等为动机的暴力事件,这些暴力事件后果严重,威胁人民安全和社会稳定,同样应该引起重视。因此本文首先筛选GTD数据库中2006~2020年的车辆冲撞数据,并以这些数据为基础信息,扩展收集各种官方公布信息、新闻媒体报道以及现场视频资料等;又扩展收集了2006~2020年间其他原因发生的各种汽车冲撞案例,建立了全面、准确的车辆冲撞案例集,案例集包含车辆冲撞案例175个。
1.2 可能性评估指标构建
建立科学、全面且有针对性的指标体系是可能性评估中至关重要的一部分,指标体系的构建决定了可能性评估模型的准确度和合理性。传统风险管理流程中可能性评估通常称为威胁分析,威胁包括敌方的数量和类型、敌人作案手法、工具类型、运用武器等。
通过对收集的车辆冲撞案例分析,发现车辆冲撞事件具有很高的关联度。首先对事件发生的背景、经过、人员、后果、影响等细节进行挖掘与整理,从事件发生的可能性影响因素的角度出发分析影响事件发生可能性的共性因素,如当车辆进行安装爆炸物等重度改装,车辆冲撞袭击发生的可能性会大幅度增加;人群高度密集的场所更容易发生车辆冲撞事件;车辆在大型附近或人群聚集场所附近出现如逆行、进行道路行驶、反复出现在同一路段等车辆行驶异常行为时,车辆冲撞事件发生的可能性也随之增加。
对车辆冲撞案例进行高频词汇分析,同时参考人群密集高风险场所风险评估指标体系,从“攻”与“防”角度出发对车辆冲撞事件的成因进行分析,结合专家经验,建立车辆冲撞威胁可能性评估指标体系,得到两个一级指标,敌手能力和目标吸引力。敌手能力包括:敌方的动机、战术、武器、能力等,用于描述敌手即发动袭击的可能性。目标吸引力是指袭击目标自身的影响力,举办活动的规模等,主要用于描述成为袭击目标的可能性。从敌手能力和目标吸引力两个一级指标出发,共确定二级指标16个。可能性指标体系如表1所示。

表1 可能性指标体系
1.3 指标分级标准
根据风险管理原则与实施指南等相关国家标准,结合传统风险评估方法和专家经验,对各指标进行分级[6]。一级指标敌手能力下确定4个二级指标,一级指标目标吸引力下确定3个二级指标。参考车辆碰撞试验等相关国内外标准及车辆冲撞相关实验数据,确定每个指标的分级标准,再根据车辆冲撞数据分布情况及车辆冲撞特点对分级标准进行调整。各个指标分级及其赋值标准见表2和表3。

表2 一级指标敌手能力下二级指标分级及赋值表

表3 一级指标目标吸引力下二级指标分级及赋值表
1.4 数据集的构建
依据输入指标分级及赋值表,对收集建立的案例集(详见1.1)的每个案例的各项可能性评估指标进行赋值,得到车辆冲撞可能性评估指标数据集。
在数据处理过程中发现,少数车辆冲撞事件对社会危害较小并未引起媒体的关注,导致这些事件相关信息缺失,个别指标存在空缺值。为保证建立的数据集的严谨性和可靠性,对指标数值空缺超过两项的不完整数据进行删除,其余空缺值选用该指标中位数填充处理。
机器学习过程中最重要的部分是对输入数据的特征值进行抓取,而目前国内外发生的车辆冲撞事件并不能覆盖此类事件发生的可能性的全部特征,需要进行数据插补,补充极端情况指标数据,包括各指标的极高或极低等级以维持数据特征完整性。
最终得到车辆冲撞事件威胁发生可能性评估指标数据集,数据量为300条。车辆冲撞威胁发生可能性分值为数据标签。
1.5 数据集的扩展
蒙特卡洛方法(Monte Carlo)是一种基于概率论的随机抽样方法,可以实现对小样本数据扩充。蒙特卡洛方法的思想起源于18世纪Buffon投针实验,实验创造了用随机模拟估计预测量的新方法[8]。ChenGang等人2019年利用蒙特卡洛方法构造虚拟样本补充到数据集中,解决了因样本数量不足导致结构件寿命预测准确率低的问题[9]。
蒙特卡洛方法在进行大量随机模拟实验后通过随机抽样得到满足变量分布的虚拟样本,最后将这些虚拟样本加入到原始数据实现数据集扩充。直接采样、接受拒绝采样与重要性采样是最常见的3种蒙特卡洛采样方法[10]。本文选取接受拒绝采样方法,拒绝采样适用于原分布式未知的情况,同时数据的维数不会影响蒙特卡洛方法的复杂性,因此这一方法适合解决车辆冲撞威胁可能性评估数据扩充问题。使用蒙特卡洛方法将可能性数据集扩充后从中选取900条数据用于后续神经网络的训练。
2 基于BP神经网络的评估模型构建
2.1 BP神经网络
BP(Back Propagation)神经网络是Rumelhart和McClelland等科学家于1986年提出的一种深度学习算法[11], BP神经网络模型通过建立机器的多隐含层模型并使用大量数据进行训练来学习有用的特征,从而达到提高分类、预测的准确性的目的。BP神经网络是一种前馈型神经网络,其核心是利用误差不断修正权值和阈值。BP神经网络为3层结构,输入层、隐含层、输出层,每一层都由一定数量的神经元(节点)组成,每一个神经元以其自身的拓扑结构进行运算,共同完成整个神经网络的计算,神经元拓扑结构如图1所示。xi为神经元输入,ωi为连接权值,选取最便捷的线性加权求和可得神经元净输入Netin为:
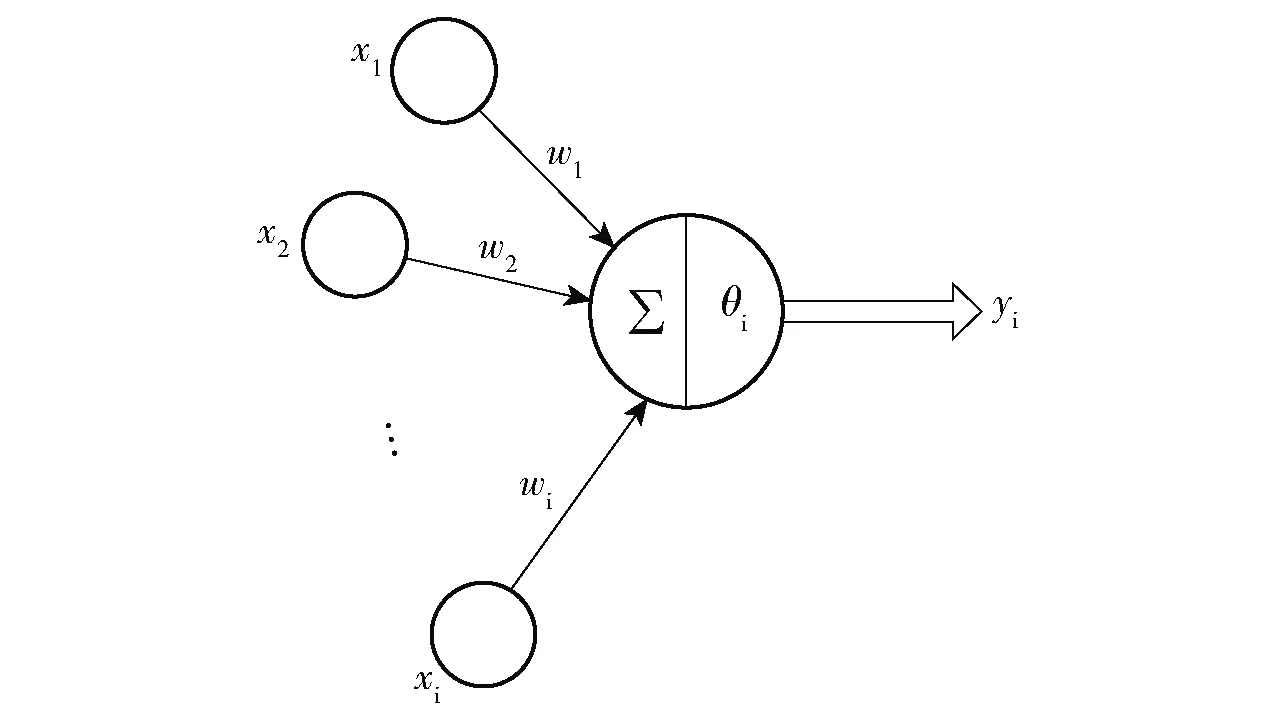
图1 神经元拓扑图
(1)
θi表示该神经元的阈值,f为激活函数,此时可以得到神经元输出:
yi=f(Netin-θi)
(2)
BP神经网络整个算法流程包括两个部分,第一个部分是信号经过输入层、隐含层、输出层向前传播,第二部分是误差反向传播,在这一部分使用梯度下降法来更新参数,误差经过输出层、隐含层、输入层不断反向传播,依次修正各层之间的权重和偏置,最终使得预测的输出不断逼近期望输出,达到所期望的目标精度。
2.2 BP神经网络模型构建
车辆冲撞威胁可能性评估数据为整数型数据,两个整数之间的关系实际意义不大,这些无价值的信息会给机器学习模型带来信息干扰。为了解决上述问题,在机器学习模型建立前对数据进行独热编码(One-Hot Encoding)处理,使可能性评估模型变成多分类模型。
独热编码又被称为one-hot编码或一位有效编码,可以用于解决多分类问题。独热编码利用状态寄存器对每一种状态进行编码,每一个状态都有自己的寄存器,因此只有一位寄存器出于有效状态。独热编码方式是一种易于实现的编码方式,其在处理非连续数据时具有很大优势,独热编码不需要解码器就可以实现,此外一定程度上实现了特征扩充[12]。车辆冲撞威胁可能性评估的数据为等级数值,是不连续的整数,因适合使用独热编码方式进行编码。
神经网络的稳定性、收敛速度、预测精准度都依赖于训练算法和网络结构,网络结构主要包括网络层数和各层的神经元节点个数。BP神经网络的模型结构及其参数设置如下。
(1)输入层
输入层为的输入数据为对手数目、对手是否有犯罪前科、场馆举办活动规模等7个可能性评估指标的分值,输入层有7个变量,其节点数为7。
(2)隐含层
对于隐藏层的设定,需要考虑隐藏层的层数和各层神经元的个数这两个重要的内容。隐含层的层数越多模型越复杂,越适用于解决复杂问题。车辆冲撞威胁可能性分析模型复杂程度不高,但其数据特征不够明显,特征提取存在一定难度。在实验过程中首先将隐含层设置为一层,在尝试变换隐含层节点数后测试集准确度始终不能达到40%。当隐含层增加到两层,准确大幅提升。经过实验最后确定隐含层数为两层。进行多次的测试与验证,综合数据集与大型场馆可能性评估的实际情况,得到最优隐含层设置为隐含层第一层为20个节点,隐含层第二层为10个节点,此时训练速度和精度都达到了最优状态。
(3)输出层
输出层的输出数据为大型场馆发生车辆冲撞事件的可能性,数值分为1~5个整数数字,代表可能性的5个等级。输出数据只有可能性这一个变量,基于独热偏码方式输出层节点数量设为5。
(4)参数设置
除上述参数外,迭代次数、学习率、以及误差的计算等BP神经网络参数需要设置。经过系列实验最终确定迭代次数设置为10 000,学习率设置为0.02,克服了梯度消失的问题,加快了训练速度。选用均方根误差(MSE)进行误差的计算。其公式如公式(3),其中yi为真实值i为预测值。
(3)
使用Python3.8、TensorFlow2.0完成BP神经网络构建。分割上文所构建的数据集,80%作为训练数据,20%作为测试数据,训练BP神经网络。
综上,最终确定车辆冲撞威胁可能性评估的BP神经网络的拓扑结构如图2所示。

图2 BP神经网络拓扑图
2.3 BP神经网络模型结果分析
模型准确率曲线如图所示如下图3所示,可以看出在5 000次迭代时得到相对最好的效果。最终的准确度为60%。

图3 BP神经网络准确度曲线
3 基于PSO- BP神经网络的评估模型构建
传统BP神经网络已经广泛应用在各个领域,是成熟的研究方法,但在应用车辆冲撞威胁可能性评估问题上时容易陷入局部最优解,此外BP神经网络过度依赖初始方案和初始参数。为更好建立大型场馆面向车辆冲撞的可能性评估模型,本文使用了粒子群算法优化BP神经网络模型,解决了模型容易陷入局部最优解的问题,大幅提高了模型准确度。
3.1 粒子群优化算法
群智能(Swarm Intelligence)方法灵感源自观察自然界中蚁群、蜜蜂群、鸟类以及鱼类等生物群体的行为机制[13]。大量个体想要完成复杂的任务需要相互配合,每个较大的生物群体有自己的相互协作方式,群智能算法是模仿这样的行为的算法。群智能算法中较为典型的算法有蚁群算法和粒子群优化算法等。群智能优化算法中引入了随机数和随机初始化,相比于其他优化算法群智能优化算法对初始方案的依赖程度较低,可以用于处理各种复杂问题,应用领域十分广泛,渐渐成为主流优化技术,在数据挖掘、计算智能、工业应用、生物、经济等领域都有重要的应用[14]。
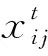
(4)
(5)
BP对于初始权重的设置是随机的,初始权重直接影响模型的预测效果。PSO- BP神经网络使用粒子群算法对BP神经网络进行优化,把BP神经网络预测精度作为粒子群算法的优化目标,寻找使得预测效果达到最佳的BP神经网络的最优初始权重,从而得到最优预测模型。PSO- BP神经网络的流程图如图4所示。

图4 PSO- BP流程图
3.2 PSO- BP模型构建
构建PSO- BP神经网络模型需要对PSO算法进行设定,在PSO算法中种群规模是一个非常重要的参数,种群中所包含的粒子数决定了网络的复杂程度,不但影响了模型的收敛速度更影响了模型预测的准确度,粒子数过少可能会导致找不到最优解,粒子数过大又会使计算时间过长,结合实践经验及本论文所研究问题的特征,设置粒子个数为3。粒子矩阵形状设置为3×20×20。学习因子设置为0.02,惯性权重均设置为0.8。
使用Python3.8、TensorFlow2.0完成PSO- BP神经网络构建,将上文所构建的数据集进行分割,80%作为训练数据,20%作为测试数据,作为输入数据输入神经网络,再对数据集进行标准化处理后开始模型的训练、预测及效果评估。
3.3 PSO- BP模型结果分析
模型误曲线如图5所示,可以看出随着迭代次数的增加误差下降的非常快,在8 000次迭代后误差变化幅度减小,在10 000次迭代时得到最好的效果。使用PSO- BP算法避免了陷入局部最优解情况发生,获得拟合区间,模型能快速抓取到车辆冲撞威胁可能性评估数据集的特征。图6为模型训练准确度的变化曲线,模型经过10 000次迭代后得到最终的准确度78.8%。模型训练耗时短收敛快,不会陷入局部最优解,误差小准确度高。未经优化的BP神经网络的准确率为60%,PSO- BP神经网络准确度更高,效果更稳定,对于车辆冲撞事件可能性评估有更好的预测效果。
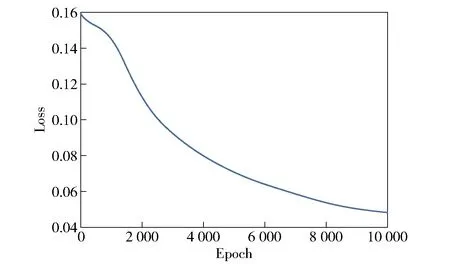
图5 PSO- BP误差曲线
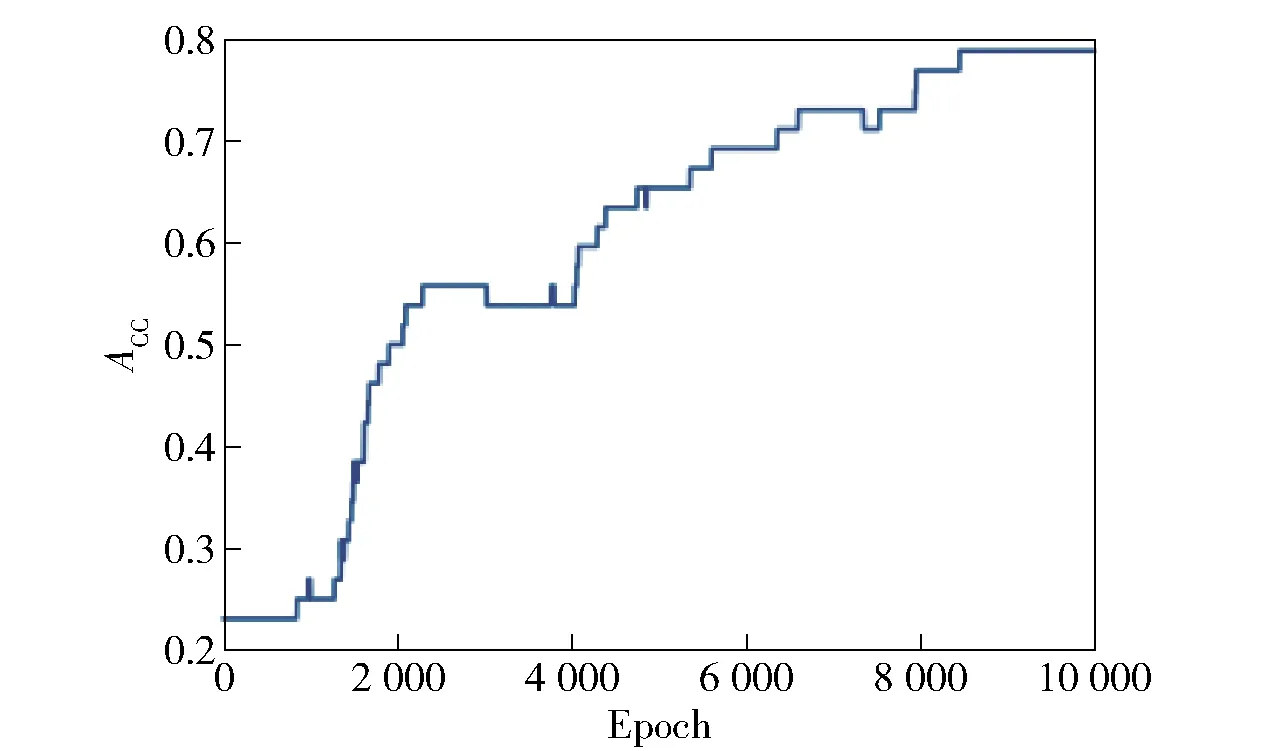
图6 PSO- BP准确度曲线
为验证本文提出的PSO- BP神经网络模型的有效性及可用性,额外选取遗传算法改进BP神经网络(GA- BP)模型和基于sklearn的决策树模型同前文构建的BP神经网络模型和PSO- BP神经网络模型进行对比实验,结果如表4所示。经对比,PSO- BP神经网络模型的测试集准确度明显优于其他3种模型。PSO- BP神经网络能很好地处理多分类问题,适合用来解决面向车辆冲撞威胁的可能性评估。

表4 模型准确度对比表
3.4 指标权重获取
根据PSO- BP神经网络模型反推指标体系中各指标权重,权重雷达图如图7所示,三级指标权重排列表如表5所示。从其排列可知在车辆冲撞威胁发生可能性指标体系中人群密集程度和场所知名程度权重显著大于其他指标,指标权重符合车辆冲撞威胁可能性评估的客观事实,符合专家预期。因此,当人群密集程度显著增大时应及时增加巡逻守卫力量。知名度较高的场所应注意人车分流同时完善报警系统,避免车辆冲撞事件的发生,将损失降到最低。
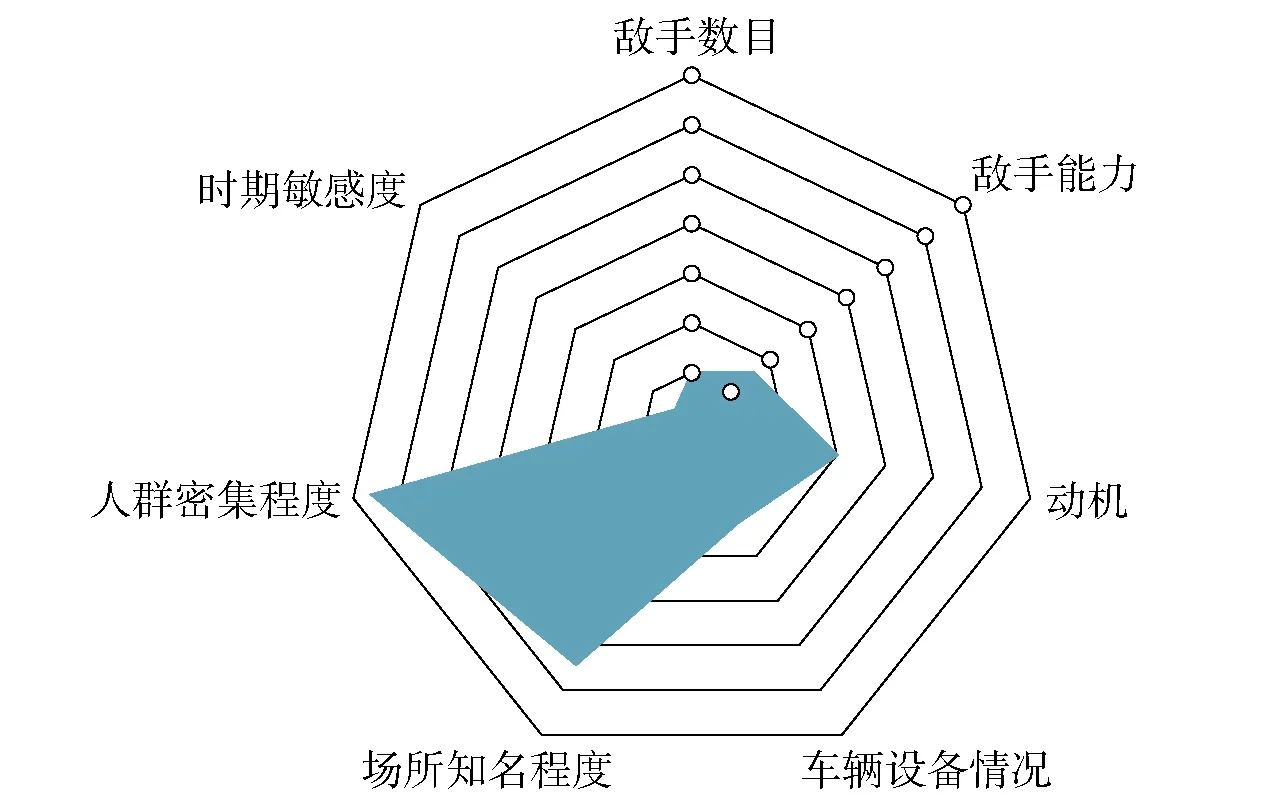
图7 指标权重雷达图
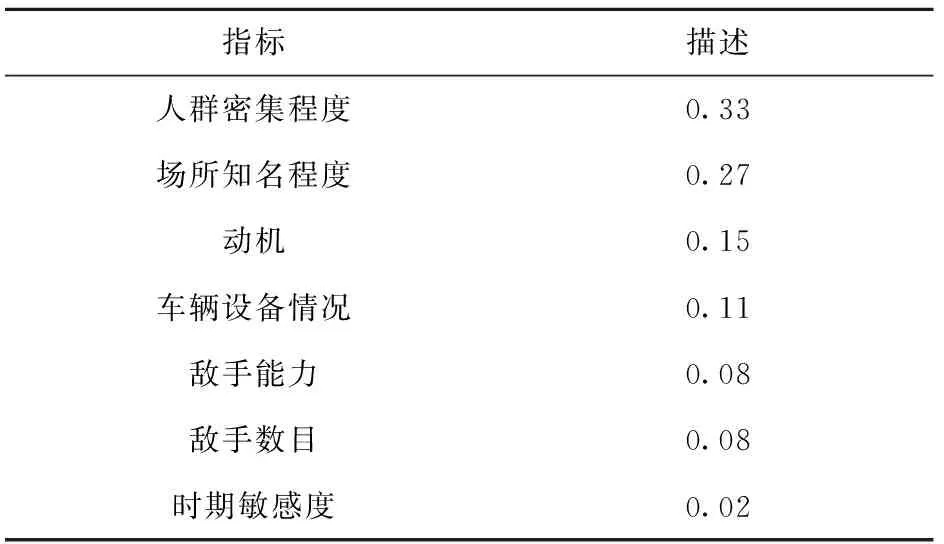
表5 三级指标权重排列表
4 结论
针对传统评估方法缺少客观性评估的问题,构建了基于深度学习的车辆冲撞威胁可能性评估模型,解决了传统可能性评估方法缺少定量客观性评估的问题。首先对国内外近15年间引起媒体广泛关注的车辆冲撞事件进行分析与整理,形成车辆冲撞案例集,建立车辆冲撞威胁可能性评估指标体系,构建车辆冲撞威胁可能性评估指标数据集;其次,使用蒙特卡洛方法对数据进行扩充;然后,在BP神经网络模型的基础上引入粒子群优化算法,并进行对比实验。结果表明,本文提出的方法在性能上提高了18.8个百分点,并得到7个三级指标的对应权重,所得权重符合车辆冲撞威胁可能性评估客观事实。实验结果表明本文所提方法具有较高的准确性和算法稳定性。
提出的基于深度学习的车辆冲撞威胁可能性评估模型目前只能实现对威胁发生可能性进行静态评估,下一步将考虑扩展指标体系并结合公安情报数据,对威胁发生可能性进行动态评估研究。
