EP-FXT 聚焦镜真实表面状态的性能模拟方法*

祝宇轩 陆景彬 陈勇 王于仨 杨彦佶 韩大炜 崔苇苇 赵晓帆 丛敏 李天明 吕中华3) 王皓迪

1) (吉林大学物理学院,长春 130012)

2) (中国科学院高能物理研究所,粒子天体物理重点实验室,北京 100049)

3) (中国科学院大学,北京 100049)

后随X 射线望远镜(follow-up X-ray telescope,FXT)是爱因斯坦探针卫星的主要载荷之一.为了获取高信噪比的数据,实现对观测天体的高精度定位,FXT 使用Wolter-I 型X 射线聚焦光学系统,该系统一直是X射线空间天文观测中的重要设备.根据Wolter-I 型的聚焦原理,结合实际的加工特点,利用蒙特卡罗模拟算法对影响光学成像质量的几个关键参量,如表面粗糙度、面形误差进行了模拟,结合模拟结果对各参量的作用效果进行了分析.之后利用PANTER 实验室提供的聚焦镜性能测试结果对模拟方法进行了验证,同时对面形误差参量进行了限制.最终聚焦镜结构热控件半能量宽度(half energy width,HEW)模拟与实测结果基本一致.该模拟过程可以很有效地应用于聚焦镜加工工艺的摸索,为FXT 的聚焦镜测试和标定工作提供参考.结合实测标定数据,该模拟方法生成的有效面积、渐晕和点扩散函数等可用于在轨观测标定数据库.

1 引言

聚焦型X 射线望远镜一直是X 射线天文观测中的重要仪器,聚焦观测方式使观测数据具有高空间分辨、高信噪比的特点,是X 射线天文学进入精密观测时期后的主流方案.从20 世纪80 年代起,一批聚焦型X 射线望远镜陆续发射升空,其中有代表性的有HEAO-2[1],Chandra[2],XMM-Newton[3]和eROSITA[4,5]等.

国内的X 射线空间观测近十几年也在逐步发展完善,其中硬X 射线调制望远镜的成功发射更是我国X 射线天文领域的里程碑式成果[6,7].为了获得更为精细的观测数据,我国相继规划提出了包括爱因斯坦探针(Einstein probe,EP)[8]和增强型时变与偏振天文台(enhanced X-ray timing and polarimetry mission,eXTP)[9,10]在内的多个聚焦型X 射线望远镜项目.EP 卫星于2017 年正式立项,计划于2023 年发射.EP 搭载宽视场X 射线望远镜(wide-field X-ray telescope,WXT)[11]和后随X射线望远镜(follow-up X-ray telescope,FXT)[12],可以实现大视场的全天监测和深度后随的定点观测[8].EP-FXT 使用了与eROSITA 结构类似的聚焦光学系统,具有较高的空间分辨(目标优于 30′′)和有效面积(目标优于340 cm2@1.49 keV)[12],是国内X 射线聚焦天文观测中的代表.

本文设计了FXT 的聚焦镜性能模拟软件,对影响成像质量的各项误差进行了数学模型的描述,利用性能实测数据对模型参数进行限定,对模拟软件进行了验证.结果表明,该模拟算法能很好地还原聚焦镜的各项光学性能,可以为聚焦镜的研制积累经验;结合标定数据,该方法可以很好地应用于FXT 的标定工作中,辅助标定数据库的建立.

2 FXT 聚焦镜性能模拟

2.1 光学原理

X 射线相对于可见光能量较大(典型能量为0.1—120 keV),常规的光学聚焦方式无法应用于X 射线聚焦中.1923 年,康普顿提出了X 射线的全反射,当X 射线以极小的角度(典型值小于 3◦)入射到极光滑的介质表面时(介质表面粗糙度均方根(root-mean-square,RMS)约为0.5 nm),会发生全反射[13].基于这种掠入射的X 射线聚焦技术,1975 年Wolter[14]提出了三种双镜片Wolter 构型,其中的Wolter-I 型可以使用多层嵌套结构,增大有效面积,被广泛地应用于X 射线天文观测中,包括EP 和eXTP 在内的国内外多颗聚焦型望远镜均使用了Wolter-I 构型.我国2016 年发射的脉冲星导航实验01 星(X-Ray pulsar vavigation-I satellite,XPNAV01)也使用了Wolter-I 构型的聚焦镜[15,16].

除此之外,还发展了其他类型的X 射线聚焦光学系统,如EP-WXT 的光学系统就采用龙虾眼构型(Lobster-eye)[17],其利用Lobster-eye 视场大的优点,可以实现约3600 平方度的大视场监测[11].

Wolter-I 型聚焦镜由抛物面内反射镜和双曲面内反射镜组成,两段镜片同轴共焦.如图1(a)所示,平行于光轴入射的光线经由两段镜片的反射,最终汇聚在系统焦点F处.单层Wolter-I 型聚焦镜的收光面积是有限的,为了增大有效面积,提高观测数据的信噪比,一般采用如图1(b)所示的多层嵌套方式,各层镜片均同轴共焦.

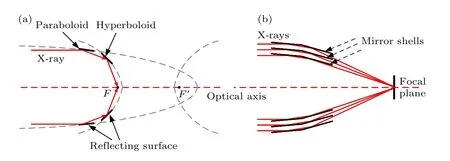
图1 (a) Wolter-I 型聚焦镜光路示意图;(b) 多层嵌套结构示意图Fig.1.Schematic diagram of (a) optical path of Wolter-I focusing mirror and (b) multi-layer nested structure.

FXT 采用双望远镜系统(A 套和B 套),两系统均采用了Wolter-I 构型[8],其中A 套聚焦镜由欧洲航天局(european space agency,ESA)提供,B 套聚焦镜拟采用德国马克普朗克地球外部物理研究所(Max Planck institute for extraterrestrial physics,MPE)提供的eROSITA 飞行备份件.单套聚焦镜采用54 层嵌套结构,入射端内径范围为76.28—356.53 mm,镜长300 mm (抛物面和双曲面各150 mm),焦距为1600 mm.同时为了给B 套聚焦镜提供备份方案,也积极开展国产聚焦镜的设计和研制工作[18−21].FXT 聚焦镜的加工选用镍电铸复制工艺[22−24].如图2 所示,首先根据设计参数通过车削和超精密抛光的方式制作模具,然后在模具表面电铸一层镍单质,利用一定方式脱模,即可复制模具的形状和表面状态.

镍复制方法生产的聚焦镜成像精度在很大程度上受机械加工精度的影响.为了对聚焦镜的性能进行深入的研究,结合聚焦镜的生产特点,完成了聚焦镜性能模拟算法,并根据聚焦镜的测试数据对模拟算法进行验证,对模拟参数进行限定.

2.2 模拟方法

一般情况认为加工精度对聚焦镜表面状态的影响从尺度上主要分为高频的表面粗糙度和低频的面形误差两方面.如图3 所示,当需要考虑的误差尺度与X 射线波长相当时,粗糙度误差会引起X 射线的散射效应(X-ray scatter,XRS)[25];面形误差通常对应较大的一个空间尺度,这一尺度的误差会导致光线在较大空间尺度上的偏折效应,可以直接采用几何光线追迹的方式.

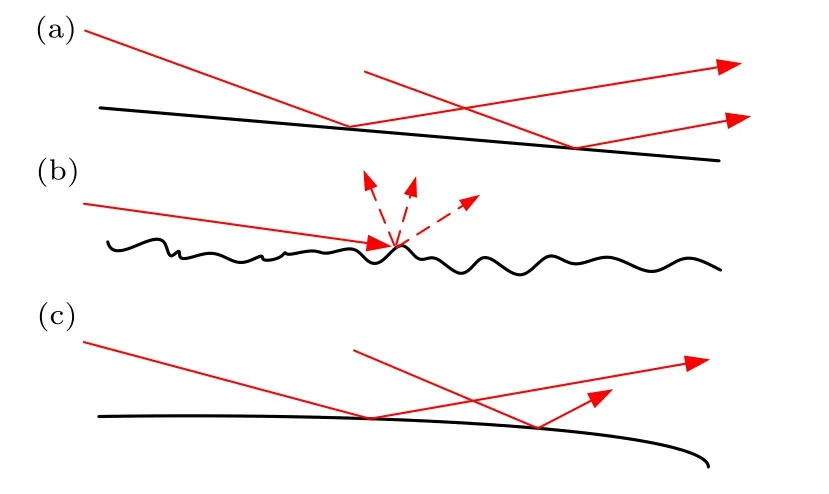
图3 (a) 理想镜面的反射;(b) 高频表面粗糙度误差下的XRS 效应;(c) 低频面形误差下的大角度偏折Fig.3.(a) Ideal Reflection;(b) XRS effect under high frequency error;(c) large angle deflection under low frequency error.

2.2.1 粗糙度误差

一般常用粗糙度的RMS 来表征镜片的粗糙度误差.当RMS 与入射光子的波长相当时,传统的几何光线追迹的模拟无法适用于XRS 的模拟,光子的反射按照一定的概率分布被散射到各个方向上,散射光子的分布服从Debye-Waller 定律[26]:

其中Is和Ii分别为散射光子强度和反射光子的总强度;σ为粗糙度RMS,单位为 nm;λ为入射光子波长,单位为nm;θi为光子的掠入射角.对于光滑且各向同性的表面介质表面,小角度散射(|θs−θi|≪θi)的归一化散射强度在散射角为θs时的分布与镜片表面的功率密度谱(power spectral density,PSD)相关[27,28]:

式中P(f) 是镜片表面的PSD,f为RMS 给定的空间频率.考虑XRS 时,.PSD 的形式取决于镜片的表面状态,一般的形式是近似幂律函数[29,30]:

其中K为归一化常数,单位为 nm3·nm−n,典型值为1 nm3·nm−1.5.由以上分析可知,XRS 效应取决于光子能量和RMS.结合(1)式和(2)式,可以得到散射概率和散射角度的分布情况,如图4 所示.

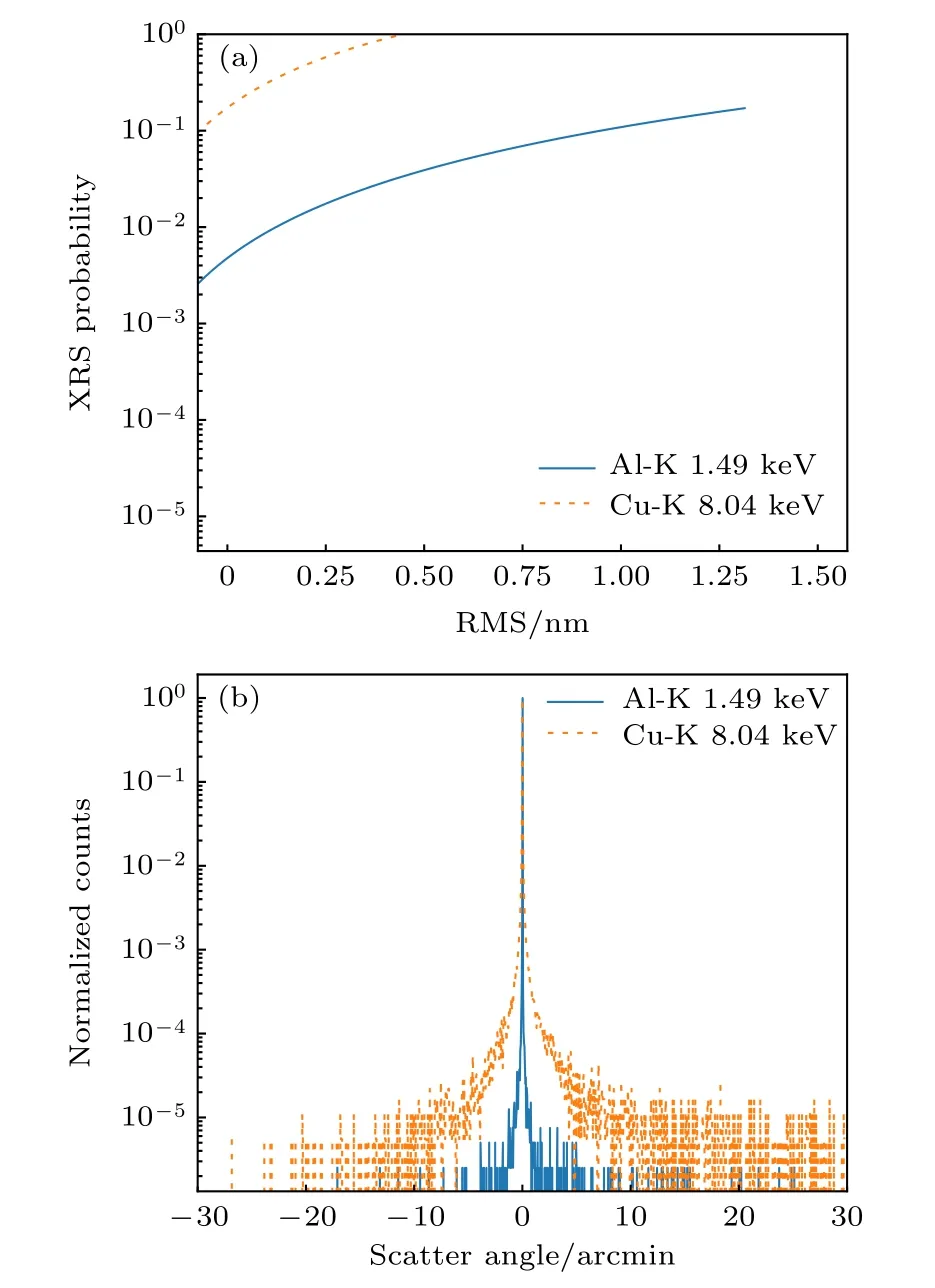
图4 (a) θi 0.7◦ 时散射概率随RMS 的变化;(b) RMS=0.5 nm 时,不同能量下的散射角分布Fig.4.(a) Variation of scattering probability with RMS value at θi 0.7◦;(b) scattering angle distribution at different energies when RMS=0.5 nm.

入射能量较低时,散射概率相对较小,散射角也分布在一个很小的范围内(±5′);能量增大时,散射概率随RMS 的增大明显增大,当能量为8.04 keV,RMS=0.75 nm 时,散射概率已达到0.4.由此可见XRS 效应直接与X 射线能量和RMS 相关.

2.2.2 面形误差

大尺寸空间下的面形误差对聚焦镜成像质量的影响与能量无关,可以使用几何光学的光线追迹进行很好的模拟.一般的方法是从模拟参数出发,假定在理想的镜面上进行反射,面形误差会对反射面法向量产生扰动,扰动的形式一般采用高斯分布的数学形式[31].对于机械加工引入的面形误差,Zombeck 等[32]进行了详细的介绍,他们的测试表明,在列举的几种误差形式中只有两种对光学性能的影响较重要.按照这一结论,可以将面形误差的扰动相应地分解为轴向和径向两个方向,如图5 所示.在法向量V模长一定时,面形对V的扰动可以分解为对α1和α2大小的干扰,换言之,整体扰动可以分解为对V1模长和V2方向的变化.

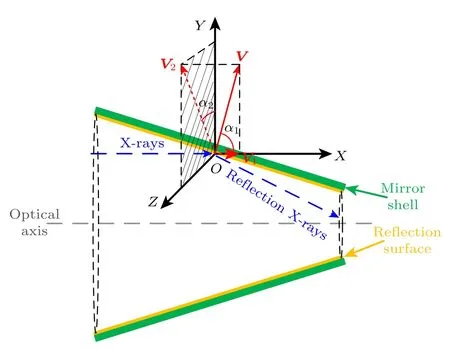
图5 镜片二维剖面下面形误差扰动分解示意图.O 点为光子在反射面上的入射点,XOY 面平行于纸面,YOZ 面平行于聚焦镜入射平面,X 轴与光轴平行,为方便显示,进行了一定的夸张Fig.5.Decomposition diagram of surface error disturbance under two dimensional (2D) section of mirror.Point O is the incident point on the reflecting surface,the XOY and YOZ planes are parallel to the paper plane and incident plane of the mirror respectively,and the X axis is parallel to the optical axis.

2.3 模拟参数分析

天文观测上一般用能量包围函数(encircled energy function,EEF)来描述成像能力,EEF 代表以光斑峰值处为中心向外扩展的圆形区域的积分亮度随扩展直径的变化曲线.在EEF 中,可以用半能量宽度(half energy width,HEW)描述光斑的展宽,HEW 表征EEF 中积分亮度达到50%时的直径;同时,为了描述背景光子或散射光子强度,一般还会使用W90 (90%光子直径).以FXT 的最外层镜片#1 镜(大端内径356.52 mm,中间内径348.48 mm,小端内径323.92 mm,厚度约为0.54 mm)为例,根据前两节中介绍的算法,对聚焦镜进行模拟,分析各参数对成像性能的影响.

为了研究两个扰动分量对成像质量的影响,在不考虑XRS 的情况下,分别对两个方向的扰动单独进行模拟,分析其对HEW 的影响,如图6 所示.对比两条曲线,V2方向的旋转扰动分量对HEW的影响相比V1方向的影响几乎可以忽略不计.当V1方向的扰动σ1达 到 10′′时,HEW 已经达到37.25′′±1.55′′.在之后的模拟中,为了简化模型,取σ25′′,对HEW 的影响约为 0.4′′.

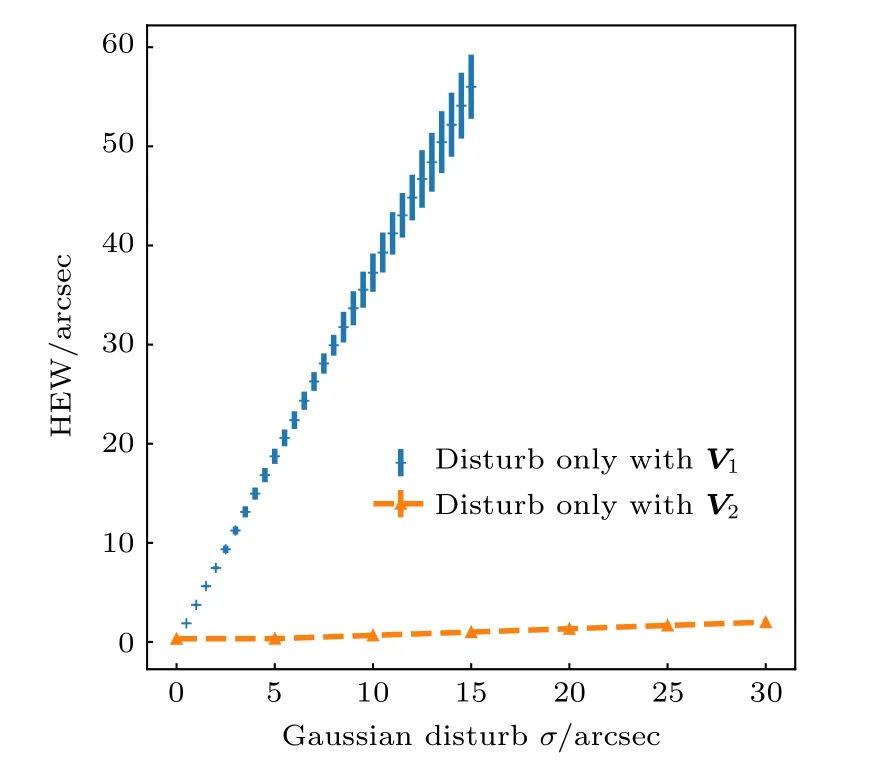
图6 高斯模型下的扰动分量对光斑HEW 的影响.其中十字点为 V1方向扰动分量,虚线为 V2 方向扰动分量Fig.6.Influence of disturbance component on spot HEW in Gaussian model.The cross point is the disturbance component in V1 direction,and the dotted line is the disturbance component in V2 direction.

在完成了面形误差对成像质量影响的分析后,可以利用(1)式—(3)式将XRS 效应叠加到面形误差之上,使光斑的点扩展函数(point spread function,PSF)更加接近真实结果.如图7 蓝色实线所示,面形误差使理想的光斑从一点扩展为具有一定展宽的高斯分布;在XRS 效应的作用下,如黄色和绿色点线所示,高斯分布的PSF 形成了散射的边缘特性.而且XRS 效应也如(1)式和(2)式中所述,能量增大,散射概率增大,边缘的平台占比增大.

图7 XRS 对光斑PSF 的影响(RMS=0.5 nm,σ1 2′′,σ2 5′′)Fig.7.Effect of XRS on spot PSF (RMS=0.5 nm,σ1 2′′,σ2 5′′).

按照这种模拟方式,模拟不同能量和不同表面粗糙度RMS 下XRS 效应对成像质量的影响,结果如图8 所示.可以看出总体上,XRS 效应随RMS增大而显著增大,HEW 和W90 随RMS 的增大而增大;XRS 效应随能量增大而增大,8.04 keV 的HEW 和W90 随RMS 的增量明显大于1.49 keV.综合图8(a)和图8(b)可以看出,XRS 效应主要影响PSF 的边缘光子,影响W90,如图8(b)所示,RMS=0.75 nm,能量为8.04 keV 时,散射概率急剧增大,W90 急剧恶化(约 1300′′).

图8 三种不同 V1方向扰动 σ1 下粗糙度RMS 的影响 (a)对HEW 的影响;(b)对W90 的影响Fig.8.Influence of roughness RMS under three different σ1 :(a) on HEW;(b) on W90.

3 模拟结果与参数限定

利用模拟算法,对有效面积和渐晕曲线进行了模拟,并与实测的渐晕曲线进行了对比.其中聚焦镜反射率随角度和能量变化的数据来源于CXRO(the center for X-Ray optics)[33].根据实测的成像结果对模拟算法中面形误差的模拟参量进行限定.需要指出的是,模拟过程中的光子入射能量与表面粗糙度为影响有效面积的两个重要参量,考虑到全反射和有效面积对聚焦镜粗糙度RMS 的要求,RMS 指标典型值为0.5 nm,本节中RMS 值均取为0.5 nm (实际测量的RMS 也约为0.5 nm).为了方便与测试数据对比,本节中所有模拟结果除特殊标明入射能量外,其余结果均为测试所用Al 的Kα线(1.49 keV).

3.1 有效面积和渐晕曲线

模拟了不同能量下FXT 聚焦镜的有效面积,如图9(a)所示.为了遮挡空间环境中的可见光,同时降低观测较强天体源时探测器的事例堆积效应(pile-up 效应),FXT 在探测器前预设了几种不同遮光膜档位,可以通过转轮进行调节.遮光膜为聚酰亚胺基底镀铝膜,根据材料厚度可以分为thin,medium 和thick 三种[34],图9(b)为膜对X 射线的透过率.模拟了三种膜对有效面积的影响,如图9(a)中橙、绿、红三线所示.可以看出,遮光膜对低于2.0 keV 的有效面积衰减较为严重,大于5 keV 时,基本没有影响.两种典型能量下的模拟结果如表 1 所列,未加遮光膜时聚焦镜有效面积可以达到(401.96±3.02)cm2@1.49 keV,能很好地满足FXT目标要求.同时在使用厚膜时,1.49 keV 处有效面积衰减严重,降至273.22 cm2.

表1 FXT 聚焦镜有效面积模拟结果Table 1. Test simulations of effective area of FXT focusing mirror.

对FXT 聚焦镜鉴定件(quality module,QM)进行了渐晕曲线模拟和测试结果对比.QM54 层镜片均具有光学性能,测试结果由MPE 的PANTER实验室[35]提供,其中渐晕曲线的测试结果可以用双高斯经验函数拟合[36],如图10 中虚线所示.对比模拟结果(如对应颜色的散点所示)表明,模拟与实测渐晕曲线趋势基本一致[37],这说明模拟方法能很好地应用于对有效面积和渐晕曲线的研究.在FXT 聚焦镜渐晕和有效面积标定过程,可以使用标定数据结合模拟结果的方法,生成在轨标定数据,为标定工作提供参考.

3.2 面形误差模拟参数限定

如第2 节所述,影响成像质量的主要有XRS 和面形效应.首先对XRS 的模拟算法进行验证,根据第2 节,为了简化模型,粗糙度RMS 取0.5 nm.图11 为散射比例的实测与模拟结果对比,其中实测结果为QM 成像光斑边缘散射光子的统计结果.

从图11 可以看出,能量较低时(C 的 Kα线,0.277 keV),实测与模拟结果相差较大(约0.02);但是随着能量的增大,两者基本保持一致(相差约0.004).在实测中,颗粒污染也会引起XRS[38],能量较低时,由粗糙度引起的散射光子不足1%,此时污染造成的散射效应要明显高于前者,但在实测的光斑中统计散射光子时无法区分两者,导致实测光斑的散射光子统计比例占比要高于模拟值;随着入射能量增大,粗糙度导致的XRS 光子比重明显增大,其他原因导致的散射光子比例明显下降,模拟与测试结果的差距变小.总体来说,对XRS 的模拟与实测结果基本一致,能很好地描述聚焦镜表面由于粗糙度产生的XRS 效应.

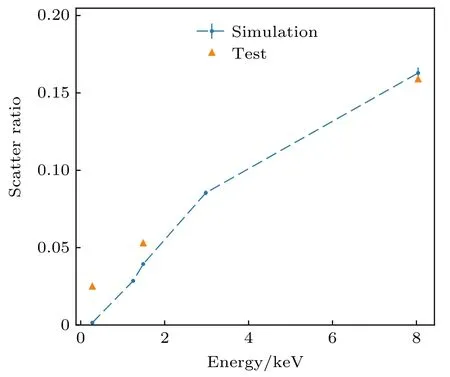
图11 RMS=0.5 nm 时散射比例实测值与模拟值对比Fig.11.Comparison between measured and simulated scattering ratio when RMS=0.5 nm.

在完成了XRS 模拟与实测的对比后,可以利用表 2 中聚焦镜结构热控件(structural-thermal module,STM)的HEW 测试结果对面形误差的模拟方法进行验证,限定STM 面形误差对应的扰动参量大小.STM 由MPE 提供,其中6 片镜片具备光学性能,分别为#1,#24—#27 和#54.如表 2所列,#1 镜片在1.49 keV 时的HEW 明显高于其他两组镜片,这是因为#1 镜片在测试过程中发生了不可逆的应力形变,光斑形状也发生了明显的三角形畸变[39].

表2 STM 在入射能量为1.49 keV 时测试结果[39]Table 2. Test results of STM@1.49 keV[39].

如图12(a)所示,前期利用高能物理研究所标定大厅的百米束线对STM 进行了进场测试,测试结果也显示STM 整体光斑呈现明显的三角形畸变.其他两组镜片的测试结果表明,在不考虑#1 镜片的三角形畸变的情况下,聚焦镜的角分辨基本可以达到 25′′.而考虑#1 镜片的形变作用后,STM 三组镜片整体光斑的EEF 如图12(b)所示,HEW 约为 32.8′′±0.12′′,W90 约为 163.2′′±3.12′′.

图12 (a) STM 成像结果(使用FXT 焦平面探测器pnCCD,单像素尺寸 75µm×75µm,像素数 384×384,中间红色方形区域的放大图如上图所示);(b) STM 成像结果的EEF 曲线Fig.12.(a) Imaging and (b) EEF results of STM test (using FXT focal plane detector pnCCD,single pixel size is 75µm×75µm,pixel number is 384×384 and the enlarged view in the middle red square area is shown in the upper in panel (a)).

按照这种性能特点将STM 分成两种,一种是未发生其他应力形变的#24—#27 和#54 镜片,一组是发生应力形变的#1 镜片.首先通过对σ1模拟,得到如图13 所示的σ1与HEW 的对应关系.HEW为 25′′对应的σ1约为 6.5′′,第一种镜片的面形误差扰动参量基本可以限定为σ16.5′′,σ25′′.

图13 RMS=0.5 nm,光子能量为1.49 keV,σ2 5′′ 时HEW 随 σ1 的变化Fig.13.Variation of HEW with σ1 when RMS=0.5 nm,photon energy is 1.49 keV and σ2 5′′.

之后在#1 的面形误差的模拟过程中,在以上σ1,σ2扰动的基础上,圆周方向每隔 120◦附加额外的扰动,来模拟应力形变.扰动模型在圆周方向符合正弦分布,光轴方向沿光路线性递减(即镜片的入口端形变程度最大).调整扰动参数(入口端峰值形变扰动约为 12.6′′),达到#1 的实测HEW指标.如图14(b)中的EEF 曲线所示,HEW= 48.54′′,W90= 166.51′′.

图14 (a) #1 镜三角形畸变成像模拟结果(焦平面探测器为pnCCD);(b)模拟光斑的EEF 曲线Fig.14.(a) Simulation results of triangular deformation (focal plane detector is pnCCD);(b) simulated EEF.

在对STM 的两种镜片分别进行了模拟参数的限定后,对整体三组镜片进行了模拟,图15 为模拟结果.为了更直观地对比光斑形状,将模拟与测试光斑沿焦平面探测器的一个方向进行投影,如图15(a)所示.从图15(a)可以明显看出,在只考虑高斯形式面形误差的情况下(蓝色虚线),一维投影的展宽明显小于实测结果(橙色方形点).加入三角形变后(绿色三角点),投影图像基本与实测结果相同,两者在散射光子比重上也符合得很好(红色箭头所示区域).图15(b)的模拟和实测的EEF曲线也基本一致.对比图12 和图15,模拟W90 为158.88′′,略大于测试结果.光斑的W90 主要受散射光子的影响,导致这一偏差的原因主要是污染引起的散射[38].

图15 (a) STM 模拟与实测光斑的一维投影;(b) STM 模拟光斑的EEF 曲线Fig.15.(a) One dimensional projection of STM simulated and test spot;(b) simulated and test EEF curve.

模拟与测试光斑对比结果可知,本文提出的模拟方法在完成聚焦镜的模拟参量限定后,可以很好地还原实测光斑的PSF.在实际聚焦镜的标定过程中,可以利用标定数据结合模拟的方式,完成标定数据库的建立工作.

4 结论

为了深入研究和发展X 射线聚焦镜的研制,本文介绍了针对EP-FXT 的X 射线聚焦镜性能模拟算法.利用算法对各种参数进行了模拟和分析,结果显示:散射概率随粗糙度误差RMS 和能量的增大而增大,随之光斑HEW 和W90 也增大,而且增幅直接与能量有关,能量越高,增幅越明显;面形误差扰动分量的V1是影响HEW 的主要因素,当σ110′′时,光斑的HEW 约为 35.25′′±1.55′′.

在完成了对各参数的分析后,对有效面积和遮光膜影响进行了模拟.利用QM 测试结果,对渐晕曲线和XRS 效应的模拟进行了验证,模拟结果与测试结果基本一致.利用STM 光斑HEW 的测试结果对STM 的面形误差模拟参量进行了限制,结果表明:在σ16.5′′时,光斑HEW 达到 25′′,与STM 的#24,#25 和#54 镜片基本一致;利用正弦分布与圆周上的额外干扰模拟了#1 镜片的三角形光斑畸变,成像结果基本达到了#1 镜片的HEW水平.之后模拟了STM 三组镜片总的性能,模拟结果表明,在加入三角形畸变的模拟后,光斑的一投影展宽与实测结果符合得很好,EEF 曲线也基本一致,最大相差在 5′′左右.

综合考虑,该模拟方法可以很好地应用于聚焦镜基本性能,如有效面积、渐晕曲线等的研究,结合标定数据,可以为在轨标定数据库提供参考.对真实表面状态的模拟方法,可以很好地建立加工误差与成像性能之间的联系,为国内聚焦镜的加工、测试和标定工作提供参考.需要指出的是,本文针对STM 测试结果的W90 指标讨论并不充分,影响W90 指标的不只有聚焦镜粗糙度引起的XRS效应,还有聚焦镜表面的颗粒物导致的光子散射和吸收.关于针对污染产生的散射和光子吸收效应,也是今后工作的一个重点方向.

感谢MPE 的PANTER 实验室提供的FXT 聚焦镜STM 与QM 的测试数据[37,39].感谢路雪峰老师、李正伟老师和张洪林同学关于算法验证工作提供的帮助和技术支持.