基于FCM的大规模群体决策方法
2022-07-19方越,吴涛,2,刘帅,陈向
方 越, 吴 涛,2, 刘 帅, 陈 向
(1.安徽大学 数学科学学院, 合肥 230601; 2.安徽大学 计算机智能与信号处理教育部重点实验室, 合肥 230039)
0 引 言
对于经典的群体决策问题(GDM),通常假设只有一小部分决策者参与决策过程。但是随着技术发展和社会需求的增加,如网络社交、网络课程、电子购物和电子商务等网络需求的提升,越来越多的人可以参与决策过程。由于决策者的个人差异以及知识和文化背景的不同,使GDM活动变得越来越复杂。这种GDM问题通常被称为大规模群体决策(LGDM)问题。
由于LDGM问题的决策者很多,成分复杂,针对决策者的聚类问题,很多学者都进行了深入的研究,Zahir,Liu,Ding等[1-3]都提出了自己的聚类方法。针对可能具有聚类结构的大规模群体,Zahir[1]提出使用相似性度量将个体分组为自然聚类的算法;Liu等[2]利用“利益群体”与实际决策信息相结合的思想,对区间值直觉模糊环境中复杂多属性大群体决策问题中的决策者进行分类,建立部分二元树DEA-DA循环分类模型,实现了多组的分类;Ding等[3]提出一种基于稀疏表示的直观模糊聚类方法来解决大规模决策问题。
但是在LGDM问题中,决策者在提供语言评估时往往会有一些犹豫和不确定,对于这种在不平衡犹豫模糊语言环境下的LGDM问题,以上这些聚类方法都显得有些力不从心。针对这个情况,Rodriguez等[4]首先提出犹豫模糊语言术语集(HFLTS),这样一来,就能更好地在犹豫模糊环境下描述决策者的决策结果;在此基础上,针对不平衡犹豫模糊语言环境下的模糊聚类问题,Zhang等[5]提出语言术语分布评估(LDA)概念,之后他又提出可以将不平衡犹豫模糊语言术语集转化为LDA算法[6],这种算法很巧妙地将决策者们不平衡的犹豫模糊语言术语转化成为统一的、方便识别与读取的基于LDA的语言术语集,这使得模糊聚类算法在不平衡犹豫模糊语言环境下LDGM中的应用更加方便、可靠。在此基础上,提出一种不平衡犹豫模糊语言环境下基于FCM的大规模群体决策方法,但是这种方法也存在着一定的缺陷,它没有计算同一集群内决策者的偏好权重。本文进一步利用模糊聚类算法产生的信息,通过使用聚类中心,引入了模糊集群中单个决策者偏好权重的概念,提出一种新的计算决策者偏好权重的方法,实验结果表明该方法的决策结果更可靠。
1 预备知识
定义1[7]设S={s0,s1,…,sg}表示一个语言术语集,其中si表示S中的第i个语言项,而g+1是基数,一个语言术语集应该满足以下条件:
(1) 集合满足:当i>j时,si>sj;
(2) 否定运算符:当j=g-i时,Neg(si)=sj。
定义2[8]S是一个语言术语集,NS(si)是si的数值尺度,i=1,2,…,g;S如果满足以下条件,那么它是一个均匀对称分布的语言术语集:
(1) 存在唯一的常数λ>0,满足NS(si)-NS(sj)=λ(i-j),i,j=0,1,…,g;
(2) 设SR={s|s∈S,s>s*},SL={s|s∈S,s 如果S是一个均匀对称分布的语言术语集,则S被称为关于数值尺度NS的平衡语言术语集,一般将S记为SB;否则,S被称为关于数值尺度NS的不平衡语言术语集。 定义3[9]设S={s0,s1,…,sg}表示一个不平衡语言术语集,称定义在S上的一个连续语言术语有序的有限子集Hs是不平衡的犹豫模糊语言术语集。 对于LGDM问题,通常需要基于决策矩阵对决策者进行分类集群,以便同一集群中的决策者彼此相似,不同集群中的决策者彼此有较大差异。聚类的方法有很多,这里使用经典的模糊均值聚类(FCM)算法,假设有n个方案A1,A2,…,An,m个属性且要把p个决策者d1,d2,…,dp分成N个集群。 决策者属于集群的隶属度由定义4和定义5计算。 k=0,1,…,p (1) 定义5[6]Zk,Zr,l和Cr,l的定义与定义4相同,则决策者dk与集群Cr,l的隶属度如式(2)所示: k=1,2,…,p;r=1,2,…,N (2) 其中,b是簇的模糊度,即b值越大,簇就越模糊。在这里,b是区间[1.5,2.5]中的一个常数。 基于隶属度,可以通过定义6进一步计算更新的集群中心的决策矩阵。 (3) t=0,1,…,g;i=0,1,…,n j=1,2,…,m;r=1,2,…,N 最后,两次迭代之间的隶属度变化[6]如式(4)所示: (4) 在这里,μ(dk,Cr,l)和μ(dk,Cr,l+1)分别表示dk与Cr,l,dk与Cr,l+1的隶属度。可以事先设定一个阈值ε>0,如果Varl>ε,则迭代继续;否则,迭代终止,dk将被分配给隶属度最大的集群。 聚类过程: 第一步:首先确定阈值ε>0,让迭代数l为0,并随机生成第l次迭代的集群中心(由一些LDA决策矩阵表示); 第二步:通过式(1)(2)计算隶属度; 第三步:通过式(3)更新中心决策矩阵; 第四步:令l=l+1,并更新隶属度; 第五步:计算式(4),如果Varl>ε,则返回第二步,继续迭代;否则,迭代终止,dk将被分配给隶集群Cr,使得:μ(dk,Cr,l)=maxu∈{1,2,…,N}{μ(dk,Cu,l)}。 假设有方案集{A1,A2,…,An},属性集{U1,U2,…,Um},现在邀请来自不同领域,有着不同文化背景的决策者d1,d2,…,dp,使用平衡语言术语集S={s0,s1,…,sg},就不同属性对方案进行决策,选出最优方案。 在文献[6]中,作者认为同一个集群的决策者是“平等”的,他给予同一集群的决策者相同的权重,但这其实不太妥当,因为即便是同一集群的决策者,他们的决策结果也存在差异,甚至这种差异有时很大,这些决策者之所以被分到同一个集群仅仅是因为在算法看来,其决策结果相对于其他人来说比较接近。所以,为了提高决策结果的可靠性,应该更进一步,对同一个集群内的决策者赋予偏好权重,而定义偏好权重,需要一个标准。 聚类中心就是一个很好的标准,一个集群的聚类中心可以在一定程度上展示这个集群的平均特征,因此,与聚类中心越接近,与所属集群之间的隶属度越大,样本点的可靠性越好,越能代表所在的集群,所以相应的偏好权重也理应越大;与聚类中心越远,与所属集群之间的隶属度越小,则样本点的偏好权重就越小。 (5) (6) 其中,i=1,2,…,n;j=1,2,…,m;r=1,2,…,N。 经过之前的计算,现在已经得到了不同集群的决策矩阵Z1,Z2,…,ZN,第r(r=1,2,…,N)个集群中决策者比例如公式(7)所示,第r个集群的模糊指数如式(8)所示: (7) r=1,2,…,N (8) 由式(7),可以得到第r个集群的归一化指数[6](r=1,2,…,N),如式(9)所示: (9) 再由式(7)、式(9),定义第r个集群标准化指数如式(10)所示(r=1,2,…,N): PAr=ηpropr+(1-η)Accr (10) 其中,η∈[0,1],是一个常数。 定义集群间的差异权重为v=(v1,v2,…,vN),其中,vr如式(11)所示: r=1,2,…,N (11) 在这里,Q(x)=xλ,0≤λ≤1,σ是1,2,…,N的一种按照PAσ(r)≥PA(r+1),∀r=1,2,…,N-1规则排序的排列。 与决策者群内权重和决策者群间权重类似,为了使决策结果更可靠,还需要计算不同属性间的权重,属性权重的计算方法如下所示: 定义8[6]假设有属性集{U1,U2,…,Um},定义属性间的权重如式(12)所示: j=1,2,…,m (12) (13) 定义9 假设有方案集{A1,A2,…,An},则Ai比Aj的优势程度如式(14)所示: pij= (14) i,j=1,2,…,n (15) 方案Ai的负流量[10]如式(16)所示: (16) 再由式(15)、式(16),方案Ai的净流量[10]公式如式(17)所示: φ(Ai)=φ+(Ai)-φ-(Ai),i=1,2,…,n (17) 步骤1 邀请决策者就所有属性针对备选方案提供其决策矩阵; 步骤2 将所有决策者的决策矩阵转换为LDA决策矩阵; 步骤3 使用模糊聚类算法,将决策者分为N个集群; 步骤4 使用式(5)计算每个集群内决策者的偏好矩阵,并根据式(6)计算每个集群的决策矩阵; 步骤5 根据式(7)—式(11)计算每个集群的权重,并使用PA-IOWA算子将集群的决策矩阵合成一个总决策矩阵; 步骤6 由式(12)计算出每个属性的权重; 步骤7 根据式(13)计算出每个方案的集体评估; 步骤8 由式(14)—式(17)计算出每个方案的净流量,以此得到最佳方案。 本文中的数据均来源于文献[11]。假设中国某市政府打算在公共交通系统中新增一条地铁线路,经过相关专家的商议后确定了4个备选方案A1,A2,A3,A4,以供进一步选择,现在,有来自不同领域,不同学术背景的20位决策者d1,d2,d3,…,d20,他们将会就4个不同的属性U1(社会影响),U2(环境影响),U3(资金预算),U4(技术可行性),对4个备选方案进行选择。 首先,按照文献[6]将决策者们的决策矩阵转化为基于LDA的决策矩阵Z1,Z2,…,Z20,在这里,使用的是一个平衡语言术语集S={s0,s1,…,s9},然后使用FCM算法对其进行聚类,并由式(5)计算每个决策者在集群中的比重,结果如下: 然后,由式(6),分别计算3个集群的决策矩阵,并且假设η=0.5,则3个集群的标准化精度指标分别为PA1=0.291 6,PA2=0.366 7,PA3=0.341 7。 设Q(x)=x1/2,则集群之间的权重为v=(0.158 3,0.605 6,0.236 1),根据PA-IOWA算子,可以计算出总体的决策矩阵,如表1所示。 表1 总体决策矩阵 表2 每个方案的集体评估 由式(12),可以得到属性权重为ω=(0.263 3,0.380 4,0.205 8,0.150 5),再由式(13),计算出每个方案的集体评估,如表2所示。 再由式(14),可以计算得到优势度矩阵: 由式(15)—式(17),易知φ(A1)=-0.082 9,φ(A2)=0.035 6,φ(A3)=-0.024 6,φ(A4)=0.071 9,则有A4≻A2≻A3≻A1,这与文献[6]得到的结果有些不同。在文献[6]中,方案A2强于方案A4,但由于本文考虑了同一集群中单个决策者的偏好权重这一因素,导致决策结果不同。 聚类中心是聚类算法的重要参数,聚类中心可以提供很多信息,但是人们在利用聚类进行决策的过程中,往往会忽略聚类中心的重要性。本文在文献[6]决策的基础上进行了改进,对聚类完成后同一个集群的决策者赋予偏好权重,最大限度地利用聚类所带来的信息,相对于文献[6],多考虑了同一集群内决策者偏好权重这一因素,这使得决策结果更加可靠。2 不平衡犹豫模糊语言环境下的FCM方法
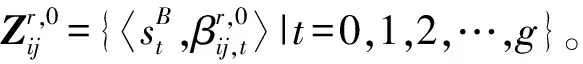
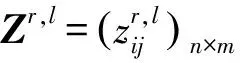
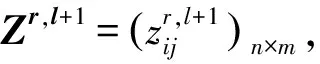
3 一种新的大规模群决策方法
3.1 决策问题描述
3.2 群决策中同一个集群决策者偏好权重度量方法
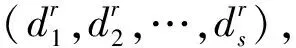
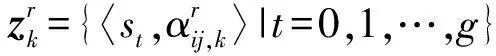
3.3 群决策中不同集群差异权重的度量方法
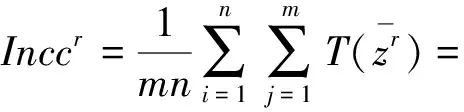
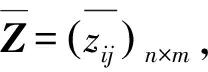
3.4 群决策中属性权重的度量方法
3.5 方案的优势度
3.6 决策流程
4 实例运用与分析



5 总 结
