线偏振激光场驱动的原子受挫双电离的波长和强度依赖

陈红梅， 李盈傧， 许景焜， 秦玲玲， 李怡涵， 何锦锦， 史璐珂，翟春洋， 汤清彬， 余本海

(信阳师范学院 物理电子工程学院, 河南 信阳 464000)

0 引言

气相原子或分子与超强飞秒激光脉冲的相互作用会产生各种新奇的物理现象, 如高次谐波产生(high harmonic generation, HHG)[1]、 高阶阈上电离(high-order above threshold ionization, HATI)[2]、非次序双电离(non-sequential double ionization, NSDI)[3]和次序双电离(sequential double ionization, SDI)[4]等。 这些现象可以通过三步再碰撞模型来理解[5]。以NSDI为例, 当激光电场与束缚库仑场相当时, 最外层的电子可以通过隧穿发射。 随后, 隧穿电子在振荡的激光电场中加速并返回, 与母核离子发生再碰撞, 并传递部分能量给另一个电子, 最终两个电子都发生电离。 另一种情况是, 如果两个曾经被电离的电子，其中一个没有从激光场获得足够的漂移能量, 则可能无法逃离库仑场的束缚, 最终被俘获到高能级里德堡态[6], 这被称为受挫双电离(frustrated double ionization, FDI)[7]。

FDI之前的研究对象主要集中在小分子, 包括H2[8]、D2[9]等。 实验上, 分子FDI可以通过测量分子离解后激发的中性碎片的动能来识别, 而这种方法并不能应用于不发生离解过程的原子。 最近, 原子FDI通过使用三体重合检测技术也被实验观察到[10]。研究发现, 随着激光强度的增加, 原子FDI呈现出由非次序区域向次序区域的明显转变。 后续的理论研究表明, 对于线偏振激光场而言, 再碰撞过程在原子FDI中起着重要的作用[11]。 而电子被俘获的物理条件取决于电离出口速度和矢势[12]。另外，圆偏振激光场和反旋双色圆偏振激光场驱动的原子FDI中的电子动力学过程也得到细致的研究。

本文利用三维经典系综模型, 研究了原子FDI对线偏振激光场的波长和强度的依赖。结果表明, FDI倾向于较短的波长且较低的强度。 在适当的激光参数下, FDI的产率甚至比人们熟知的NSDI的产率高。 此外, FDI的电离电子沿激光偏振方向的动量谱呈现明显的双峰结构, 这与最近的实验结果一致[10]。 通过反演分析FDI的所有轨迹, 发现FDI事件仍然是由于再碰撞机制诱导。 此外, 反演分析表明FDI的俘获电子往往有两个通道贡献： 1)再碰撞导致一个电子立即电离处于电离态而另一个电子处于激发态，且处于电离态的电子最终被束缚; 2)再碰撞导致双激发态, 然后在激光场的峰值附近先后电离, 且其中一个束缚态的电子最终被俘获。 对于这两种通道, 被俘获电子的电离时间窗口明显不同, 且在较短的波长和较低的强度下, 两者的时间窗口均较大。最后, 演示了FDI中被俘获电子的主量子数可以通过波长和强度来操控。

1 理论方法

精确地描述强激光场下原子双电子演化，需要数值求解相应的含时薛定谔方程。 然而, 该方法对计算机硬件设备要求非常高[13]。 目前人们使用较多的方法为经典系综方法[14-18]。 因为该方法不仅可以成功地解释实验结果, 而且可以直观地理解强场电离过程的细节, 比如回碰时间、返回能量、发射时间等。 依据经典系综模型, 两电子的演化遵循牛顿运动方程(本文采用原子单位, 除非另有说明)。

(1)

两个电子的初始位置和动量是随机分配的, 使它们满足能量约束, 即总能量等于目标原子的前两个电离势的负和. 使用氩作为目标原子, 其初始总能量是-1.59 a.u.。本文的结论同样适用于其他原子。 电子-离子核相互作用和电子-电子相互作用分别表示为

和

为避免自电离和非物理数值奇点, 软化参数a设置为1.5 a.u.,b设置为0.05 a.u.，激光未开启时, 整个系统允许演化足够长的时间(200 a.u.)并获得稳定的动量和位置相空间分布。 一旦得到初始位置和动量, 就启动激光脉冲。 两个电子都将与激光脉冲相互作用, 每个电子的演化由公式(1)决定。记录这两个电子每0.01个激光周期的能量演化, 并定义在激光脉冲结束时两个电子的能量均为正，则称为双电离(DI)事件。 如果两个电子在激光脉冲期间的某个时间的能量为正, 但脉冲结束时, 其中一个电子的能量为负, 则称为FDI事件。 每个电子的能量包括动能、核-电子势能和电子-电子势能的一半。

2 结果和讨论

图1(a)给出了0.5 PW/cm2线偏振激光场下FDI概率(三角形)、DI概率(方形)以及FDI与DI概率比值(圆形)随激光波长变化曲线。 可以看出, 在线性-对数尺度上, FDI的概率曲线随激光波长的增加呈现线性下降的趋势, 这可以定性地理解为, 波长越长, 电子波包扩散越强，从而抑制了再碰撞过程。 图1(b)显示了800 nm激光场FDI概率、DI概率以及FDI与DI概率比值与激光强度变化曲线。可以清楚地看到, FDI的概率曲线在低强度时迅速增长, 在高强度时缓慢增长。 总体而言, FDI的概率曲线与相应的DI概率曲线表现出相似的趋势。

当隧穿电子返回到母核离子发生再碰撞后, 两个电子都被发射出去, 其中一个电子在激光场结束时是否被母核离子俘获，决定了FDI或DI的发生。 因此, FDI和DI之间存在竞争关系。 在0.5 PW/cm2的情况下, 如图1(a)所示, FDI与DI的概率比随着激光波长的增加而减小(见圆形曲线)。 在800 nm的情况下, 可以看到FDI和DI的概率比随激光强度的增加而减小, 如图1(b)所示(见圆形曲线)。 因此, FDI倾向于更短的波长和更低的强度。

图2(a)和(b)分别给出了FDI事件和DI事件中电离电子沿激光偏振方向的动量分布。对于图2(a)粉色虚线和蓝色实线, 激光峰值强度相同(0.5 PW/cm2), 但激光波长不同(400 nm和800 nm)。对于图2(b)蓝色实线和红色虚线, 激光波长相同(800 nm), 但激光峰值强度不同(0.5 PW/cm2和0.1 PW/cm2)。可以看出, 在FDI事件中, 虽然电子动量分布的宽度随激光强度和波长的增加而由宽变窄, 但它呈现出与激光峰值强度和波长无关的明显双峰结构。对于DI事件, 如图2(b)所示, 其电子动量分布与FDI的类似, 如图2(a)所示。这清楚地显示了多周期激光脉冲的非次序双电离机制。理论结果与最近的实验结果符合得很好[10]。

图1 (a)激光峰值强度为0.5 PW/cm2时, FDI概率、DI概率、FDI与DI概率比值随激光波长的变化曲线; (b)激光波长为800 nm时, FDI概率、DI概率、FDI与DI概率比值随激光峰值强度的变化曲线

注：粉色虚线的激光波长和激光峰值强度分别为400 nm和0.5 PW/cm2。 蓝色实线的激光波长和激光峰值强度分别为800 nm和0.5 PW/cm2。红色虚线的激光波长为800 nm, 激光峰值强度为0.1 PW/cm2

为了理解激光峰值强度和激光波长对FDI微观电子动力学的影响, 反演分析了所有的FDI轨迹, 得到了回碰时间(tr)和双电离时间(ti2)。这里,tr定义为第一个电子第一次离开母离子核后两个电子最接近的瞬间,ti2定义为两个电子的能量刚刚第一次都变为正的瞬间。图3(a)给出了(ti2-tr)的相对概率。 可以看出, 对于这3种激光参数, 其时间差的峰值位置均大于0.1个激光周期, 表明FDI由碰撞激发场致电离通道(RESI)主导, 这与HAAN等报道的结果一致[7]。

进一步, 鉴别出FDI的电离电子和束缚电子, 图3(b)给出了被俘获电子的电离时间tir和tr之间的时间差的概率分布。

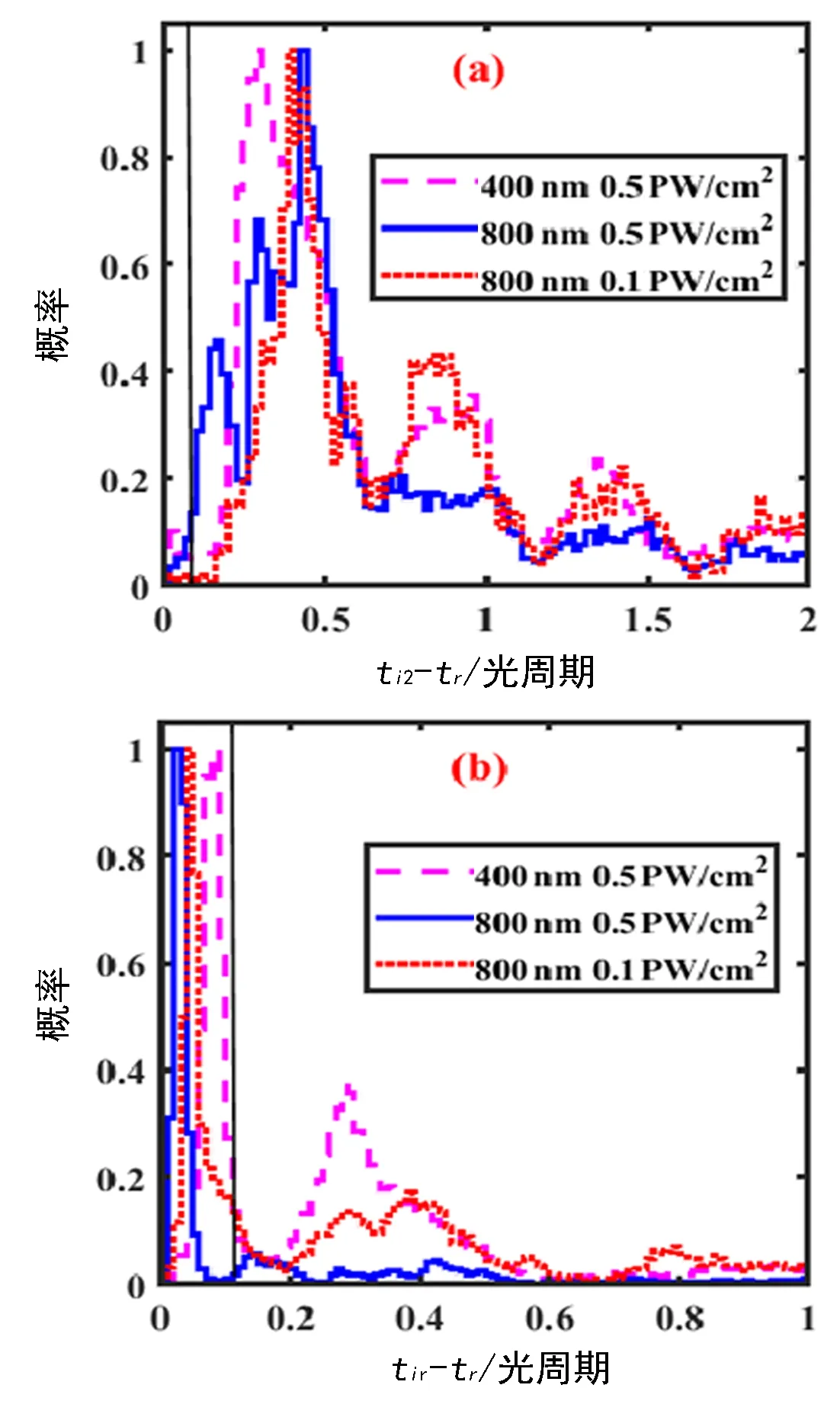
注：激光参数与图2相同。细垂线为0.1光周期的标记

这里, 定义被俘获的电子被电离的条件为: 再碰撞后能量首次为正且到母核离子的距离大于5 a.u. ，可以看到λ=400 nm和I=0.5 PW/cm2的情况下, 有两个明显的区域分布：一个集中在0.1光周期内, 对应于再碰撞后仍处于电离态的电子被重新俘获的情况； 另一个集中在0.28个光周期附近, 对应于再碰撞后处于激发态的电子被重新俘获的情况。 然后, 将FDI的轨迹分为两条通道。 通道A: 被俘获的电子在再碰撞后立即电离, 最终在激光脉冲结束时被束缚; 通道B: 被俘获的电子在再碰撞后首先进入激发态, 然后在激光场的峰值处电离, 但最终被库仑场束缚。

表1给出了被俘获电子来自入回碰电子和束缚电子的比率。结果表明, 对于通道A, 不同激光参数下的被俘获电子均主要来自于入碰电子, 而对于通道B, 被俘获电子是来自入碰电子还是束缚电子对激光参数有很强的依赖。需要注意的是, 当激光峰值强度相同(0.5 PW/cm2)时, 通道B的概率随着激光波长的增加从70%左右降低到40%左右。当激光波长相同(800 nm)时, 随着激光峰值强度的增加, 通道B的概率也从70%左右降低到40%左右。这是因为更短的波长和更低的强度导致入碰电子具有更低的返回能量, 所以两个电子再碰撞后会处于双激发态。

表1 FDI的被俘获电子由回碰电子和束缚电子贡献的比率Tab. 1 The ratio of the recaptured electron of FDI from the recolliding electrons and the bound electrons

图4给出了通道A(红色虚线)和通道B(蓝色实线)的电离电子沿激光偏振方向的动量分布。 可以看出, 在这两种情况下, 尽管通道A比通道B的动量分布的宽度更宽, 但电离电子动量分布都呈现出明显的双峰结构。

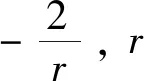
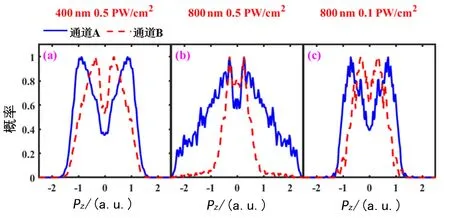
注：激光参数与图2相同, 如图所示在每个面板的最上面一行

注：每个面板中的红色虚线表示矢势A(t)。 激光峰值强度和波长显示在每个面板的最上面一行

对于通道A, 由图5(a—c)可知, 再碰撞主要发生在激光场的零点附近。 碰撞后, 入碰电子仍然有很高的速度(非常接近相应的矢量势),并立即离开母核离子。 这说明碰撞过程中的能量传递效率较低, 第二个电子只能被激发, 不能直接电离。 这就是FDI更倾向于碰撞激发后场致电离通道的原因。

对于通道B, 由图5(d—f)知, 最显著的结果是被俘获电子电离时对应的激光相位的分布。 一般来说, 当势垒被充分抑制时, 激发态电子最有可能被发射出去, 因此电离时间往往集中在激光场的峰值附近。 因此, FDI事件中的激发态电子只有在激光场达到最大值后才能被释放出来, 以获得接近于零的最终动能。 此外, 可以看到, 随着激光强度(如图5 (f)和(e)所示)和波长(如图5(d)和(e)所示)的增加, 窗口明显变窄。下面将基于simple-man模型来解释这个问题。

图6 (a) 3种激光参数下, 通道B中电子的统计电离出口速度, (b)相同激光强度下通道B的电离时间窗口示意图, (c)与(b)相同, 但波长相同Fig. 6 (a) Schematic diagram of the ionization time windows in pathway B for the same laser intensity, (b) same as (a), but for the same wavelength, (c) statistical ionization-exit velocity in pathway B for the three laser parameters

图7 3种激光参数下, FDI事件中被俘获电子的主量子数分布, (b)与(a)相同, 但为受挫单电离事件Fig. 7 The principal quantum number distribution of the recaptured electron in FDI events for the three laser parameters, (b) the same as (a) , but for the frustrated single ionization events

3 结论

FDI更青睐于较短的波长和较低的激光强度。 在适当的激光参数下, FDI事件的概率比DI事件的概率更多。在非次序双电离区, FDI电离电子沿激光偏振方向的动量分布呈现明显的双峰结构, 这与最近的实验结果一致。 反演分析表明, FDI事件以RESI通道为主。发现再碰撞过程中FDI的贡献主要有两种通道：一是入碰电子或束缚电子在再碰撞后处于电离态, 但最终被重新捕获，对于这种通道, 重新捕获电子的电离出口纵向速度与最终电离时间的矢量势大小接近；另一种是两个电子中的一个在再碰撞后进入激发态, 直到场致电离, 但最终被重新俘获， 对于该通道, 最终电离时间主要发生在激光场达到最大值之后, 时间窗口随着波长和强度的增加而显著减小。 进一步, 基于直观的Simple-man模型仔细理解了上述结果，强调激光波长和激光峰值强度在产生和控制FDI方面的重要性。 例如, 波长和强度可以用来控制FDI的产率以及被俘获电子的主量子数。