动车组换气装置用逆变器的热仿真分析
2022-07-18丁杰尹亮刘文清
丁杰,尹亮,刘文清
(湖南文理学院 机械工程学院,湖南 常德 415000)
动车组在列车交会或隧道通过时,车体内外压差会产生急剧变化. 为避免这种急剧变化的压差给乘客带来明显不适,动车组使用吊挂在车体底部的换气装置控制车内压力的变化量及变化率,使其分别小于1 000 Pa和200 Pa/s[1]. 换气装置还可与列车的空调系统协同控制车内空气环境参数,为乘客提供良好的乘车环境,是动车组的关键设备之一[2]. 换气装置由逆变器和电动送风装置两个设备组成,逆变器根据列车速度来调节电动送风装置的电源频率,进而调节风机转速. 因此,逆变器的稳定可靠运行对换气装置至关重要.
逆变器采用交直交变频原理,结构紧凑的柜体中安装有电抗器和用于整流、逆变功能的变流模块等部件. 电抗器工作产生的损耗会导致绕组温升过高而加速绝缘老化,影响电抗器的寿命[3],变流模块的开关器件使用IGBT模块,内部封装的IGBT芯片和二极管芯片的体积很小而发热量较大,导致单位体积的热流密度非常高,极易出现芯片温度过高,影响IGBT模块的可靠性. 由此可见,对逆变器进行良好的热设计是换气装置产品开发的关键环节.
李凯伟等[4]对IGBT功率模块的热网络模型及其参数辨识方法进行了综述,比较了各方法的优缺点. 杨正等[5]针对光伏并网逆变器开展了热仿真分析和温升试验验证,基于仿真结果提出了一种逆变器的结构布局和散热器结构的优化方案. Cova P等[6]对IGBT功率组件建立了流动与传热的有限元模型,基于仿真结果进行了设计方案的改进. 蒋远志[7]使用Icepak软件对光伏逆变器的散热器进行DOE试验优化设计,得出了综合最优方案. 李广义等[8]利用Icepak软件对安装有双IGBT模块的风冷散热器进行仿真分析,发现增加导风板可以改善散热器翅片间的空气流动,使IGBT模块的温度分布更加一致. 丁杰等对IGBT模块的风冷散热器[9]、翅柱式水冷散热器[10]、热管散热器[11]等散热结构开展了热仿真与试验研究. 由文献可知,仿真分析手段已成为逆变器散热设计的重要支撑.
本文以某动车组换气装置用逆变器为研究对象,首先通过电气参数计算选择合适的IGBT模块,然后由经验公式计算IGBT模块的损耗与温升,再利用FLUENT软件对逆变器进行仿真分析,最后通过试验验证热设计方案的可行性.
1 逆变器的主电路电气参数计算
图1为动车组换气装置的工作原理示意图. 逆变器为电动送风装置提供合适的工作电源,电动送风装置由一个电机带动两端的叶轮,形成进出风的两个离心风机,从车外抽吸的空气经过电动送风装置的供风通道后送入车厢,车厢内的空气经电动送风装置的排风风道后强制排出车外.
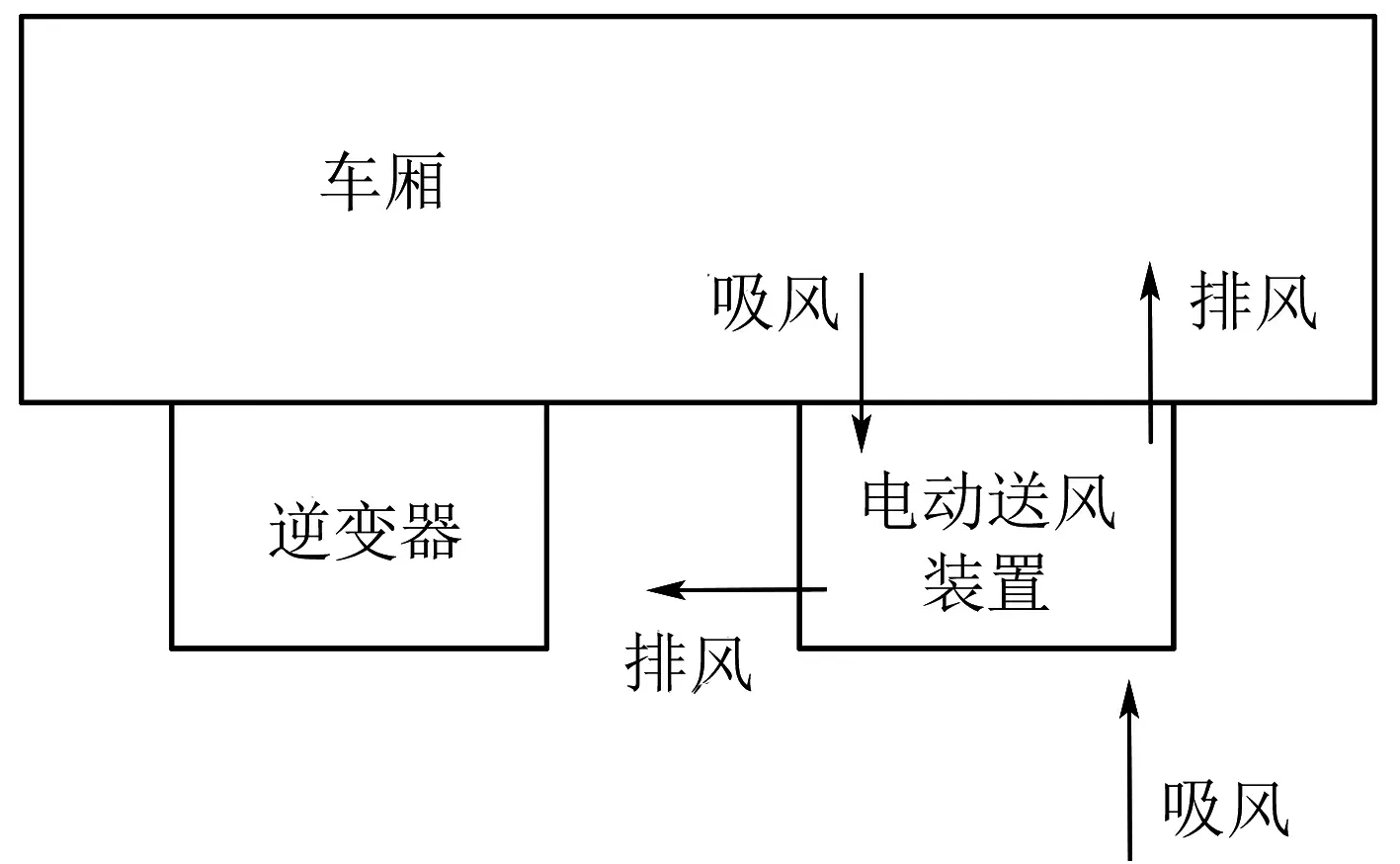
图1 换气装置的工作原理
图2为逆变器的主电路原理图. 逆变器的容量为20 kW,首先将单相AC 400 V/50 Hz输入经过整流后得到中间直流电压,再将其逆变为三相交流电输出给电动送风装置的电机.交流电的输出频率根据动车组的速度来确定,速度低于160 km/h时为53 Hz,速度高于160 km/h时为60 Hz.主电路中,输入电路部分包括接触器K1、K2及充电电阻R1,在逆变器工作前对直流支撑电容C限流充电,避免对电容及接触器产生冲击.
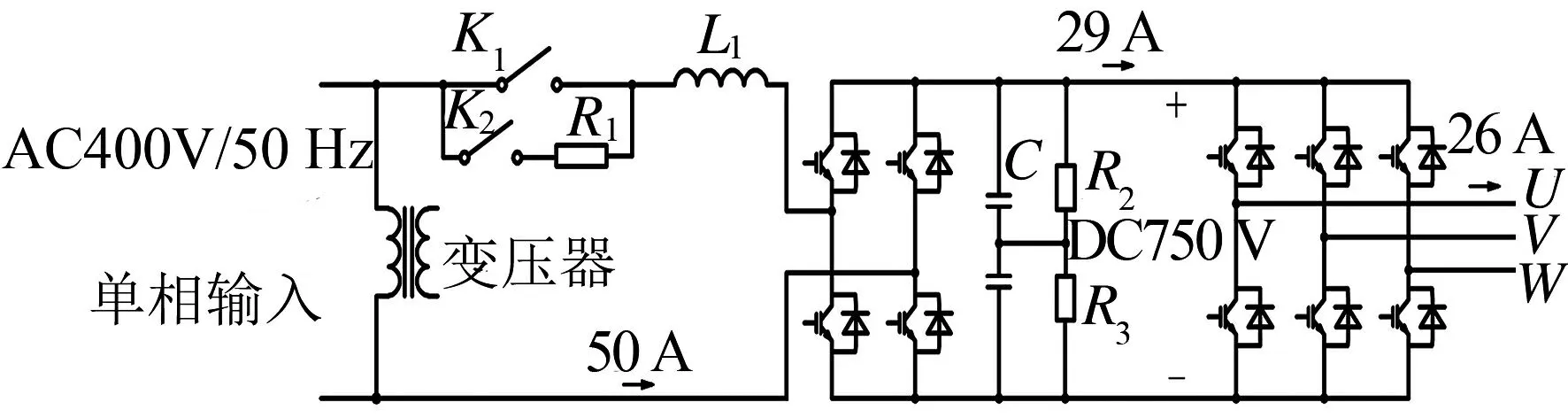
图2 主电路的原理图
中间直流电压Ud是在输入电压最大值基础上再乘以安全系数确定的,可取750V. 整流和逆变用的IGBT元件承受的最高电压为:
Umax=(k1Ud+Usp)k2
(1)
式中:k1为中间环节直流电压波动系数,取1.05;k2为安全裕量,取1.2;Usp为浪涌电压,取150 V. 由此可确定1 200 V等级的IGBT元件满足工作要求.
整流部分的额定电流Iin为50 A,要求网压下降18%时能发挥额定功率,故整流的最大电流IC为50/0.82=61 A. 考虑安全裕量后,整流用的IGBT元件最大电流为:
(2)
式中:α1为电流尖峰系数,取1.2;α2为温度降额系数,取1.2;α3为过载系数,取1.4. 选用额定电流大于174 A的IGBT元件即可满足工作要求.
逆变部分的额定输出电流为26 A,根据式(2)的裕度系数可以确定逆变选用额定电流大于74 A的IGBT元件可满足工作要求.
为了减少IGBT元件的型号数量,整流和逆变均选用额定电压为1 200 V、额定电流为200 A的BSM200GB120DN2型双管IGBT元件.
2 电气部件的损耗及温升计算
2.1 IGBT元件的损耗计算
IGBT元件中包含IGBT芯片和反并联的续流二极管芯片,IGBT芯片的损耗主要有导通损耗和开关损耗,而二极管芯片的损耗主要有导通损耗和反向恢复损耗. 为便于损耗计算,采用SPWM双极性调制的二电平三相对称桥式拓扑电路结构中,假设输出电流为正弦波,输出特性进行线性化近似[12].
IGBT的导通损耗为:
(3)
式中,Icp为正弦输出的电流峰值,Vce_sat为Icp时IGBT饱和压降,D为IGBT导通占空比,θ为输出电压与电流之间的相位角,cosθ为功率因数.
IGBT的开关损耗为:
(4)
式中,fsw为开关频率,Esw_on和Esw_off分别为峰值电流下单脉冲的IGBT开通和IGBT关断能量.
二极管的导通损耗为:
(5)
式中,Iec为门极短路时集电极最大关断电流,Vec为Iec时二极管的正向压降.
二极管的反向恢复损耗为:
(6)
式中,Erec为单脉冲的二极管恢复能量.
根据IGBT元件数据手册中的特性曲线可以得到不同工况下的参数. 逆变器输出频率60 Hz条件下的IGBT元件损耗要高于53 Hz条件,为考虑恶劣条件下的损耗及温升,取逆变器输出频率60 Hz条件下的参数进行计算及分析.
整流工况:Icp=71 A,Vce_sat=2.3 V,D=0.5,cosθ=-0.98,Esw_on=10 mJ,Esw_off=12 mJ,fsw=1 500 Hz,Iep=71 A,Vec=12 V,Erec=4.8 mJ. 可以计算出单个IGBT的Pss=12.1 W,Psw=10.5 W,PT=22.6 W,单个二极管的Pdc=14.9 W,Prec=2.3 W,PD=17.2 W.
逆变工况:Icp=37 A,Vce_sat=1.8 V,D=0.5,cosθ=0.85,Esw_on=7.2 mJ,Esw_off=9.1 mJ,fsw=4 000 Hz,Iep=37 A,Vec=1 V,Erec=3.5 mJ. 可以计算出单个IGBT的Pss=11.3 W,Psw=20.8 W,PT=32.1 W,单个二极管的Pdc=2.9 W,Prec=4.5 W,PD=7.4 W.
由于IGBT模块为双管元件,因此单个IGBT模块的损耗为上述计算的PT与PD之和的两倍.
2.2 IGBT元件的温升计算
整流和逆变的IGBT元件安装在铝材质的翅片散热器上,通过3个EBM 4214H型直流风扇进行强迫通风冷却. IGBT元件的芯片热量经焊料层、绝缘衬板、基板、导热硅脂传递到散热器,最后由冷却空气带走. IGBT元件的一维散热模型如图3所示.
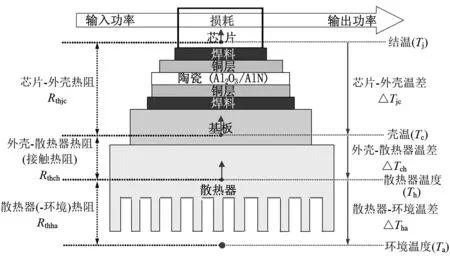
图3 IGBT元件的一维散热模型
IGBT芯片的结温为:
(7)
二极管芯片的结温为:
(8)
式中,Rthjc_T为IGBT结壳热阻,Rthha_T为IGBT壳与散热器之间的热阻,Rthjc_D为二极管结壳热阻,Rthha_D为二极管壳与散热器之间的热阻,Rthha为散热器与周围环境之间的热阻,Ta为环境温度.
根据IGBT元件数据手册可知:Rthjc_T= 0.09 K/W,Rthjc_D= 0.18 K/W,因缺少接触热阻和散热器的性能数据而假设Rthhc_T=Rthhc_D= 0.1 K/W,Rthha=0.15 K/W,环境温度Ta取40 ℃. 可以估算出整流工况的IGBT结温Tj_T和二极管结温Tj_D分别为60.53 ℃和61.57 ℃;逆变工况的IGBT结温Tj_T和二极管结温Tj_D分别为64.05和55.99 ℃.
2.3 电抗器的损耗计算
电抗器工作时会产生铁损和铜损[13],工程计算时大多通过硅钢片型号查找其单位质量损耗,再根据铁心质量计算空载损耗P0.
P0=ktPtmc
(9)
式中,kt为附加系数,Pt为铁心单位质量的铁耗,mc为铁心质量.
电抗器的负载损耗Pk包括绕组直流电阻损耗Pr、导线涡流损耗Peddy、并联导线间环流损耗Pleads以及部分结构件(如夹件、压板、螺栓等)的杂散损耗Pother.
绕组直流电阻损耗为:
(10)
式中,I1n和I2n分别为原边和副边绕组额定相电流,R1,150、R2,150分别为折算到150 ℃时原边和副边绕组的总电阻.
导线涡流损耗为:
(11)
式中,aw为垂直于纵向漏磁场方向的导线宽度,f为频率,mw为导线的总质量,Bmax为磁通密度的最大值.
杂散损耗的经验公式为:
(12)
式中,kz为电抗器厂家通过测试给出的杂散损耗系数.
电抗器的温升较难通过简单的公式进行计算,需要借助仿真分析或试验手段.
3 逆变器的热仿真分析
3.1 逆变器的几何结构
图4为逆变器及变流模块的三维结构. 逆变器主要由柜体、变流模块、电抗器、交流风机和直流风机等组成. 变流模块集成了实现整流及逆变功能的IGBT元件、驱动电路、直流支撑电容、散热器和传感器等,采用复合低感母排连接IGBT元件与直流支撑电容,可以减小主电路杂散电感,降低IGBT关断浪涌电压. 散热器的底板长度、宽度和厚度分别为504、360和16 mm,翅片的长度、高度、厚度和间距分别为260、80、2和6 mm,翅片的数量为57片.

(a)逆变器

(b)变流模块图4 逆变器及变流模块的三维结构
3.2 流动与传热仿真的理论基础
逆变器柜体内的空气流速低,空气密度变化很小,而且主要考虑稳定状态下的温度分布,因此,这属于稳态不可压缩流动与传热问题. 质量守恒方程、动量守恒方程和能量守恒方程的通用形式为[14]:
div(ρuφ)=div(Γgradφ)+S
(13)
式中,φ为通用变量,Γ为广义扩散系数,S为广义源项.对于质量守恒方程,φ为1,Γ为0,S为0;对于动量守恒方程,φ为ui(i=1~3,分别对应x、y和z方向),Γ为流体动力粘度μ,S为-∂p/∂xi+Si;对于能量守恒方程,φ为温度T,Γ为k/cp,S为ST,其中,k为导热系数,cp为定压比热容.
柜体内的空气受风机的影响,流动处于湍流状态时,还需要遵守附加的湍流输运方程.标准k-ε模型是应用非常广泛的一种湍流模型.
湍动能k方程为:
(14)
湍动耗散率ε方程为:
(15)
式中,Gk是由平均速度梯度引起的湍动能产生项,μt为湍动粘度,C1ε和C2ε为经验常数,σk和σε分别为湍动能和耗散率对应的Prandtl数.
利用有限体积法进行数值计算的流程是首先确定流动与传热问题的计算区域和边界条件;然后划分网格,生成计算节点,建立离散方程;再给定求解控制参数,对离散方程进行迭代求解;计算收敛后最终得到流场和温度场的计算结果.
3.3 逆变器的热仿真模型
建立仿真模型时,首先对逆变器的三维几何模型进行适当简化,去掉一些对散热影响小的零部件和几何特征,并将一些外形不规则的零部件做适当调整. IGBT模块被导热系数很低的硅凝胶灌封保护,绝大部分热量通过基板向散热器传递,极少部分热量通过外壳的热辐射以及功率端子的传递,故在建立IGBT模块的仿真模型时不考虑硅凝胶、外壳和功率端子的影响. 电抗器的铁心由多层硅钢片叠压而成,由于片间绝缘非常小,片数多,按实际的硅钢片结构建模计算不现实,采取将其几何结构作为一个整体而材料导热系数设置为各向异性的简化方法. 电抗器的绕组由丝包铜线和匝间绝缘组成,将绝缘层的影响折算到线圈的等效导热系数中. 三维结构的交流风机(型号为MR18-BC)可简化为二维的压力阶跃面模型,用多点折线方式对如图5(a)所示的风机特性曲线进行拟合. 变流模块的散热采用强迫风冷,在散热器翅片下端安装了3个型号为4214HU的直流风机,通过独立风道对IGBT元件进行散热,直流风机的启停由散热器底板上安装的温度继电器控制,以便于在控制IGBT元件温升的基础上延长直流风机的工作寿命. 3个直流风机位于流场模型中部,输入如图5(b)所示的风机特性进行模拟.

(a)MR18-BC型号交流风机
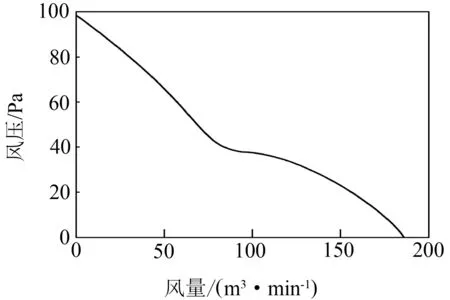
(b)4214HU型号直流风机图5 风机的特性曲线
考虑到IGBT模块与散热器之间的导热硅脂层厚度,以及IGBT模块中包含的芯片、焊料、绝缘衬板等材料层的厚度都很小,网格基本尺寸取2 mm. 抽取出的流道部分以及固体区域组成如图6所示的计算模型. 利用HyperMesh软件进行网格划分,可以得到以六面体为主,极少数为棱柱体的三维实体网格.
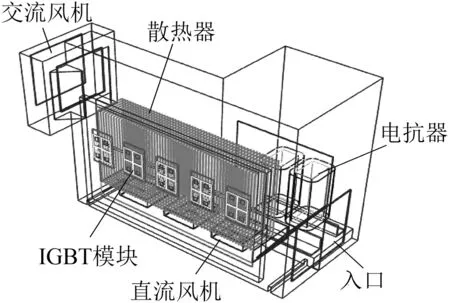
图6 计算模型
3.4 逆变器的仿真结果及分析
图7为冷却空气在流道内的流速迹线图. 在交流风机的抽吸作用下,冷却空气首先由入口进入,经过电抗器后流向变流模块的散热器翅片,最后经交流风机排出. 从流速迹线图可以看出柜体内部空气受1个交流风机和3个直流风机的共同作用,流场分布较为复杂. 整个流道中,局部区域的最高流速为9.96 m/s.

图7 流速迹线图
图8为散热器、IGBT元件和电抗器的温度分布. 图8中5#表示温升试验时整流部分两个IGBT之间粘贴的1个热电偶位置,对应温度为79.4 ℃,温升为39.4 ℃,6#和7#表示温升试验时逆变器三个IGBT元件之间粘贴的2个热电偶位置,对应温度分别为75.3 ℃和74.8 ℃,温升分别为35.3 ℃和34.8 ℃.整流部分和逆变部分的IGBT模块芯片最高温度分别为89.3 ℃和82.6 ℃,这些芯片的温度明显高出前面利用式(7)和式(8)的计算结果,其原因在于散热器热阻参数的假设并不合理,说明IGBT模块温升的准确计算是建立在计算参数合理的基础上的. 从散热器上的IGBT元件温度分布还可以看出不同位置的温度有差别,这5个IGBT元件的芯片温度并不相等,而是相差了10.8 ℃,表明仿真计算的结果能够真实地反映流场和温度场的空间分布特点. 从IGBT元件的温升数值来看,小于允许的最高工作结温125 ℃,说明IGBT元件的温升裕量较大. 电抗器的最高温度位于线圈内部,为132.76 ℃,低于绝缘材料F等级的最高允许温度155 ℃,线圈温升为92.76 ℃,低于温升限值100 ℃. 由于仿真计算选取了逆变器在最恶劣的工况下稳定工作的情形,逆变器产品实际情况中的温升要低于仿真计算结果,有利于确保产品的可靠性.
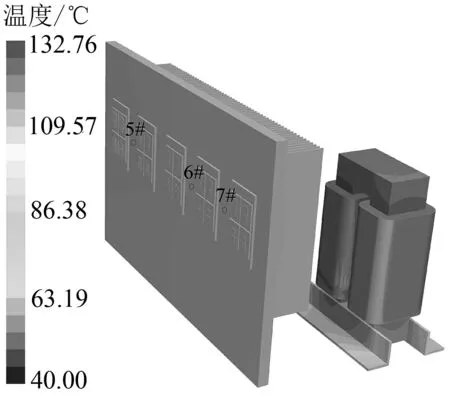
图8 温度分布
4 逆变器的温升试验验证
为验证热设计及仿真结果的准确性,在检测试验中心开展了逆变器与电动送风装置的组合试验,如图9(a)所示. 在电抗器的铁心上布置1#、2#热电偶,在靠近入口的线圈上布置3#、4#热电偶,如图9(b)所示. 试验条件为逆变器输入AC 400V,输出频率为60 Hz.

(a)试验装置

(b)电抗器的温度测点布置图9 试验现场情况
图10为温升试验得到的温度曲线. 初始环境温度为7.7 ℃,试验进行了360 min后,此时的环境温度为11.5 ℃,1#~4#的温度分别为80.2、80.3、92.4和94.5 ℃,对应的温升分别为80.2、80.3、92.4和94.5 ℃,而仿真获得的温升分别为79.1、80.8、85.6和90.8 ℃,可以看出温度高低的趋势一致,误差在7%左右. 产生误差的原因主要在于仿真计算将铁心和线圈结构通过导热系数的方式进行等效,与实际情况存在一定的差别.
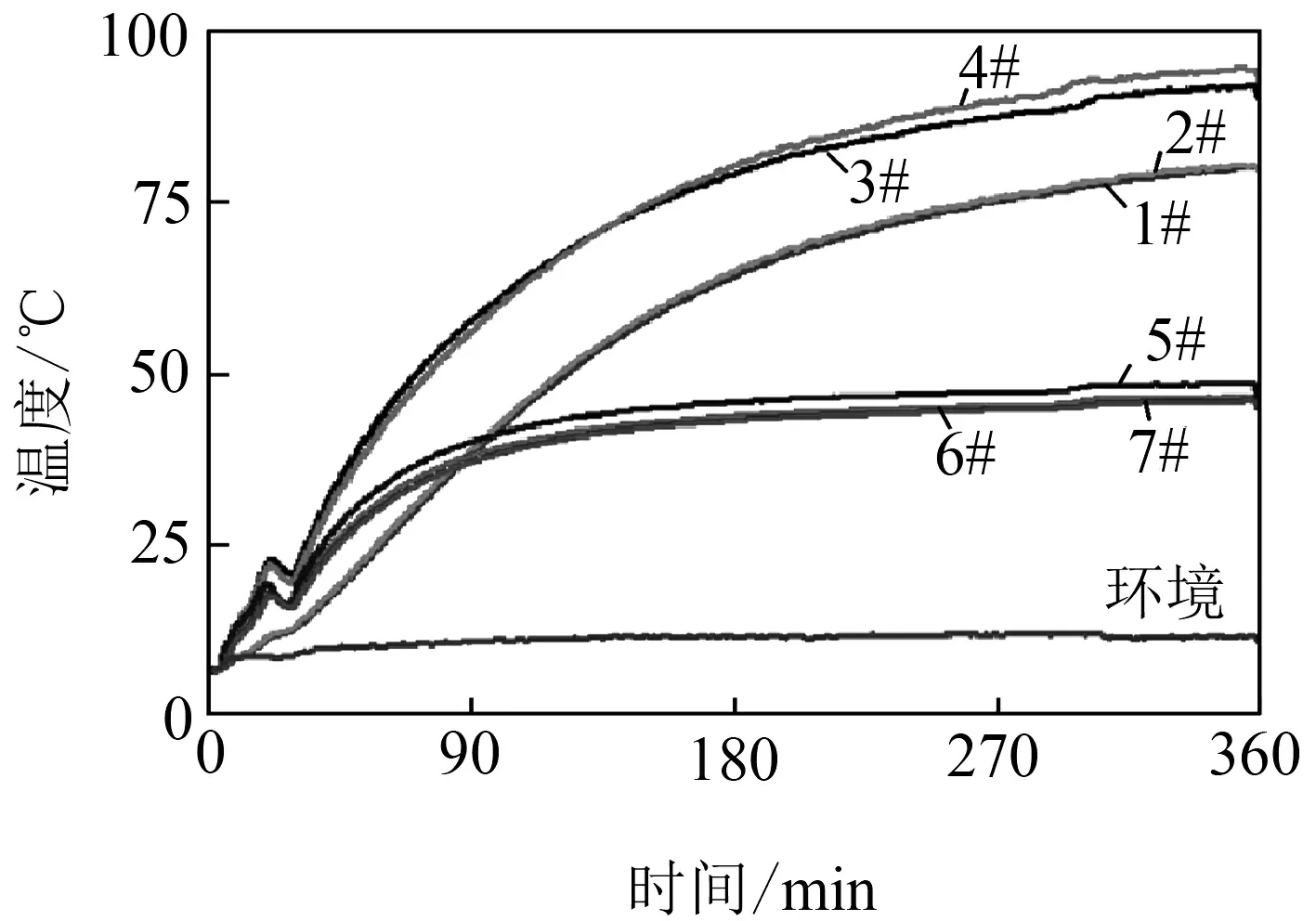
图10 温升试验曲线
试验进行到360 min时,测得5#~7#的温度分别为48.8、46.8和46.6 ℃,对应的温升分别为37.3、35.3和35.1 ℃. 与仿真获得的温升结果相比,误差在6%以内,由此可说明仿真计算的方法是可行的.
5 结论
本文对动车组换气装置用逆变器进行了电气参数计算、元件选型、热设计仿真及试验验证等工作,结论如下:
(1)逆变器在恶劣工况下稳定运行时,整流部分和逆变部分的IGBT模块芯片最高温度分别为89.3 ℃和82.6 ℃,小于允许的最高工作结温125 ℃,而电抗器的最高温度为132.76 ℃,低于绝缘材料的最高允许温度155 ℃,线圈温升低于温升限值100 ℃;
(2)仿真模型可以考虑流场与温度场的空间分布特点,仿真计算的温升误差与试验结果相比在7%左右,说明仿真计算方法及结果具有较高的准确性,可为逆变器产品的热设计工作提供理论依据.
致谢:本文受湖南文理学院博士启动基金(19BSQD26)、湖南文理学院科技创新团队基金(校办通[2020]26号)项目资助,特此致谢!
