水电机组主轴摆度信号中脉冲干扰滤除方法研究

唐拥军，赵毅峰，李超顺，周 攀

（1.国网新源控股有限公司抽水蓄能技术经济研究院，北京市 100761；2.华中科技大学土木与水利工程学院，湖北省武汉市 430074）

0 引言

随着我国能源结构改革进程的不断推进，大力开发水电能源对构建清洁低碳的能源体系、促进经济社会可持续发展具有重要战略意义。作为水电站能量转换过程的核心设备，水电机组正在向复杂化、巨型化、集成化和智能化的方向发展，其面临的安全可靠运行问题日益突出，随之而来的是水电机组运行状态监测及故障诊断系统日益受到重视和得到发展[1]。

水电机组的主轴摆度是衡量机组运行稳定性的重要指标之一，包含了丰富的机组运行信息。而实际监测得到的主轴摆度信号由于现场测试环境和设备的干扰不可避免地引入各种噪声，这对机组的运行状态评价和后续的故障诊断十分不利[2-4]。尤其是主轴测量表面存在凸起、凹陷或受磁场干扰等，使得主轴摆度信号中存在强烈的脉冲干扰时可能会对机组的运行状态产生误判，甚至有可能出现主轴摆度幅值超出停机保护设定值，从而产生非正常停机现象，给机组的安全稳定运行带来严重的负面影响。为此，有必要采用合适的方法滤除主轴摆度信号中的脉冲干扰。

小波分析具有良好的时频局部性能和多分辨率分析的特性，比较适用于分析突变和非平稳信号[5]，基于小波变换的阈值法可以较好地抑制白噪声，但对滤除脉冲干扰的效果不佳[6]。目前去除主轴摆度信号中脉冲干扰通常采用中值滤波方法，中值滤波由著名学者 J.W.Tukey 提出，中值滤波是一种非线性处理技术，其基本原理是把信号序列中一点的值用该点的一个领域中各点值的中值代替。中值滤波对高频窄脉冲干扰有较好的滤除效果，但对宽脉冲的滤除效果较差，且对整个信号的细节部分产生不利影响[7-9]。为此，本文针对水电机组主轴摆度信号提出了一种新的滤除脉冲干扰的方法。

1 瞬时变化梯度

为了更好地对本文方法进行描述，首先引入瞬时变化梯度概念，对于一等间隔离散采样信号记为xi（i=1，2，…，n，n为信号长度），信号xi在位置序号j处的瞬时变化梯度用式（1）表示：

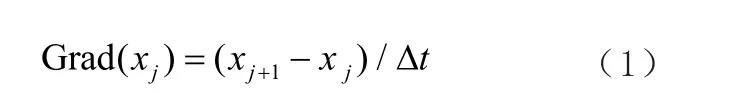
式中：Δt为采样间隔。

由于信号xi为等间隔采样信号，即Δt处处相等，信号xi在位置序号j处的瞬时变化梯度可简化为xj+1-xj，瞬时变化梯度简称为变化梯度。

因此，对信号序列进行后者减前者的运算，即可得到信号变化梯度序列，数学表达式如下：

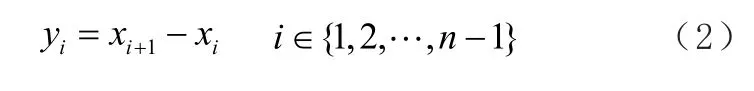
例如某水电机组主轴摆度信号如图1所示，其变化梯度序列如图2所示。由图2可知，该信号各位置处的变化梯度较小，可以说没有明显的脉冲干扰。

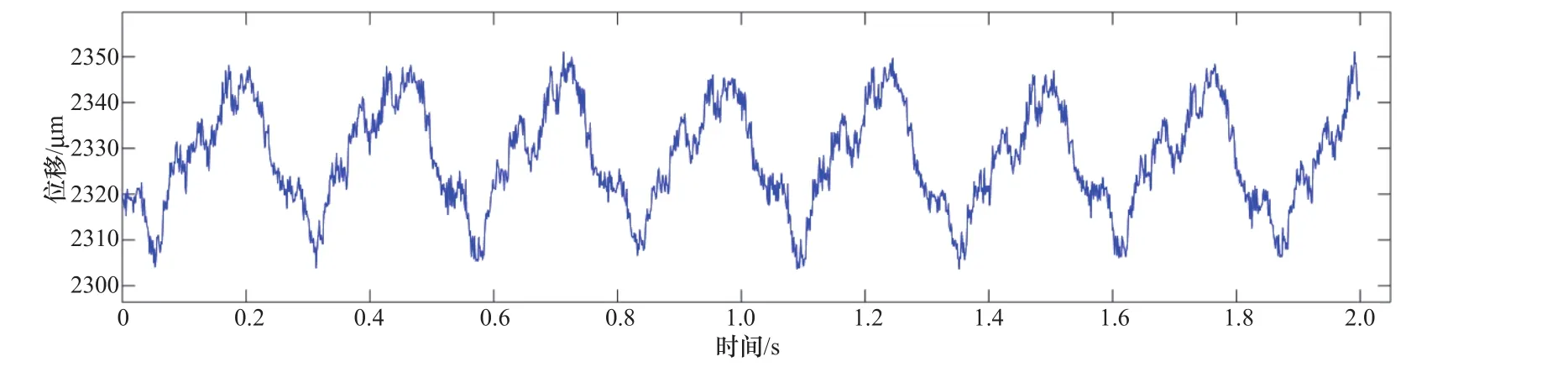
图1 某水电机组主轴摆度信号时域波形图Figure 1 Main shaft run-out waveform of a hydroelectric unit

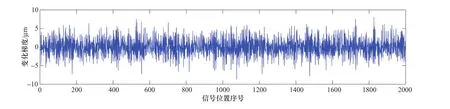
图2 主轴摆度信号变化梯度序列波形Figure 2 Waveform of main shaft run-out change gradient sequence

2 滤除脉冲方法

信号中存在脉冲干扰，意味着信号在某些位置处的变化梯度较大，因此，可以设定一正阈值和一负阈值，当信号变化梯度序列中某一元素数值大于正阈值或者小于负阈值，则认为脉冲出现，脉冲起始位置为该元素位置。正阈值和负阈值可以通过观察变化梯度序列曲线人为设定，也可以根据变化梯度序列的概率密度分布和置信度来设定。当变化梯度序列长度足够时，置信度可以采用类似正态分布的3σ原则来设定。3σ原则[10]为：数值分布在（μ-σ，μ+σ）中的概率为 0.6826；数值分布在（μ-2σ，μ+2σ）中的概率为 0.9545 ；数值分布在（μ-3σ，μ+3σ）中的概率为0.9973。置信度设定时可以采用2σ原则，认为1-0.9545=0.0455的变化梯度数据不可信，也即认为不可信数据属于脉冲数据，再根据不可信数据左右均分的原则，获得上述的正阈值和负阈值。例如某机组上导摆度变化梯度曲线如图3所示，该摆度信号变化梯度曲线明显存在周期性的脉冲现象，这说明该摆度信号存在明显的脉冲干扰。该摆度信号变化梯度序列概率密度分布如图4所示，根据2σ原则获得正阈值为68，负阈值为-63，如图4中的红色直线所示。实际应用时还可以直接设定置信度为95%或93%等，也即认为有5%或7%的变化梯度数据不可信（属于脉冲数据）。设定置信度为93%时获得的正阈值为48，负阈值为-40，如图4中绿色直线所示。

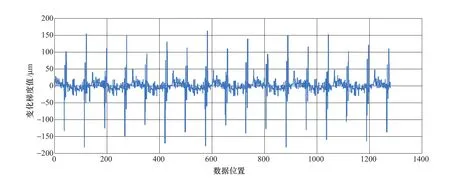
图3 某机组上导摆度变化梯度曲线Figure 3 Waveform of main shaft run-out change gradient

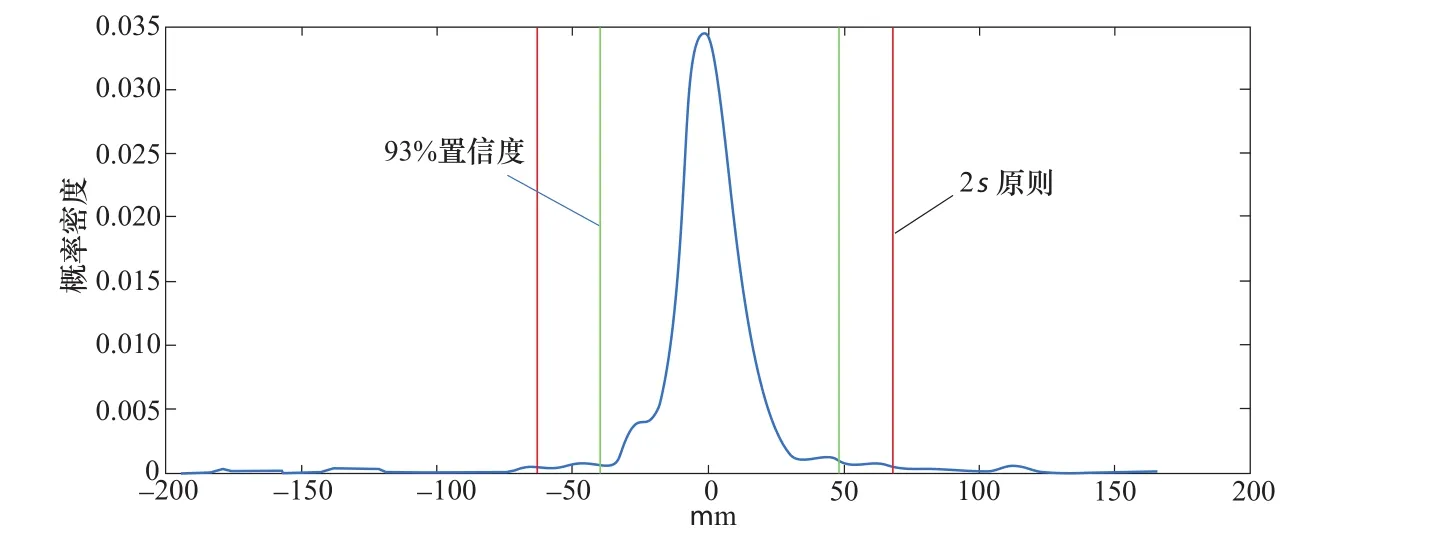
图4 变化梯度序列概率密度分布曲线Figure 4 Probability density distribution curve of change gradient sequence

获取脉冲干扰起始位置后，还需获取脉冲干扰结束位置。对于窄脉冲而言，脉冲结束位置数值与脉冲起始位置数值相差较小，对于宽脉冲而言，脉冲结束位置数值与脉冲起始位置数值可能会有一定偏差，但偏差应不大，如某机组上导摆度波形如图5所示，该摆度信号含有明显的宽脉冲干扰，图中红色圆圈区域脉冲的起始位置数值为140.2，结束位置数值为165，增长百分比为17.7%。

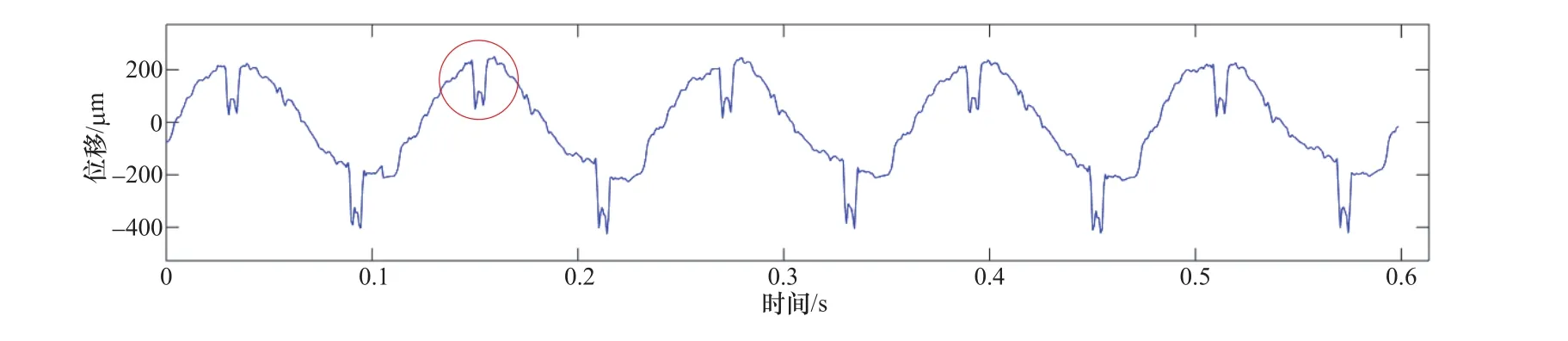
图5 某机组上导摆度时域波形图Figure 5 Upper-guide bearing run-out waveform of a hydroelectric unit

依靠人工判断每一个脉冲干扰的起始位置和结束位置费时、费力、不具可操作性，为此，本文提出利用计算机程序自动判别的方法。为简化讨论，本文以方向向下的一个脉冲为例进行论述，摆度信号记为xi，该摆度信号变化梯度序列记为Tdi，程序实现的流程如下：

方向向下的脉冲干扰具有一下降沿和一上升沿。首先根据摆度信号变化梯度序列和负阈值，自动判断出脉冲干扰的起始位置记为p0；再从脉冲起始位置的下一个位置开始判断，直到位置j其变化梯度Td(j)大于设定的正阈值，且[x(j+1)-x(p0)]/x(p0)的绝对值小于预先设定值（可设定为10%～20%），则认为j+1为脉冲干扰结束位置。特殊地，若j+1位置变化梯度也大于设定的正阈值，且[x(j+2)-x(p0)]/x(p0)的绝对值小于预先设定值，则认为j+2为脉冲干扰结束位置，若右移一位继续满足上述条件，脉冲结束位置继续右移一位。

在获得脉冲干扰的起始位置和结束位置之后，再对起始位置和结束位置之间的数据进行修正。修正方法为选取起始位置之前和结束位置之后个数均为j-p0的数据进行多项式拟合。考虑到主轴摆度信号主频通常为1倍转频信号，具有明显的正弦周期性，因此，多项式拟合的阶次选2阶。特殊地，当j-p0等于1时，则采用线性拟合计算，即所求修正数据等于脉冲起始位置与脉冲结束位置对应信号数值的平均值。

下面结合数据图对本文方法进行示例解释，某机组上导摆度信号脉冲片段及该片段的变化梯度序列数据曲线如图6所示，设定正阈值为50，负阈值为-50，脉冲结束位置相对脉冲起始位置数值变化幅度阈值设为15%，由图6（b）可知，信号片段第3个点为脉冲起始位置，脉冲方向向下。变化梯度序列第5个点数据68.94大于50，脉冲方向向上，不过信号片段第6个点数值与第3个点数值相差65.8%（以第3个点作为基准）相差较大，因此，信号片段第3个点至第6个点数据未构成完整脉冲，需继续右移求取脉冲结束位置。变化梯度序列第10个点数据154.16大于50，脉冲方向向上，不过信号片段第11个点数值与第3个点数值相差28.4%（以第3个点作为基准）大于预设值，继续右移求取脉冲结束位置。变化梯度序列第11个点数据67.24大于50，脉冲方向向上，信号片段第12个点数值与第3个点数值相差6.1%（以第3个点作为基准）小于预设值，则信号片段第12个点为脉冲结束位置。

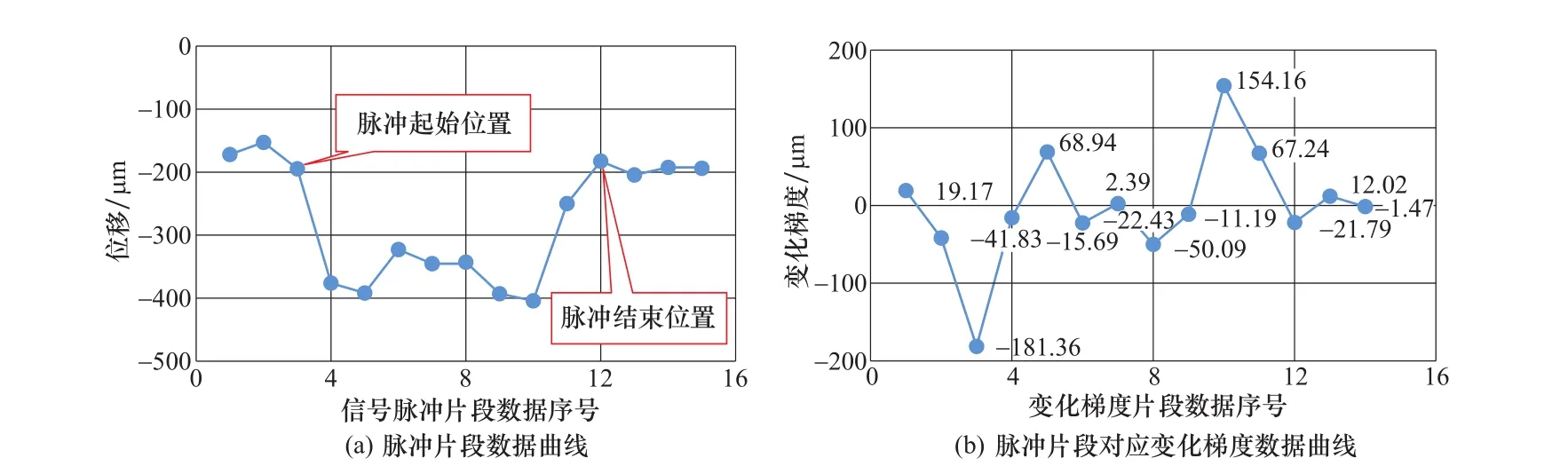
图6 某机组上导摆度信号脉冲片段及该片段的变化梯度序列数据曲线Figure 6 Waveform of pulse segment of upper guide bearing run-out signal and change gradient of it

信号片段第3个点至第12个点之间共计8个点的数据需要修正处理，于是从脉冲起始位置开始向前选取8个数据，从脉冲结束位置开始向后选取8个数据，进行二次多项式拟合，拟合结果见图7，根据拟合结果插值可求出上述8个点的数据。

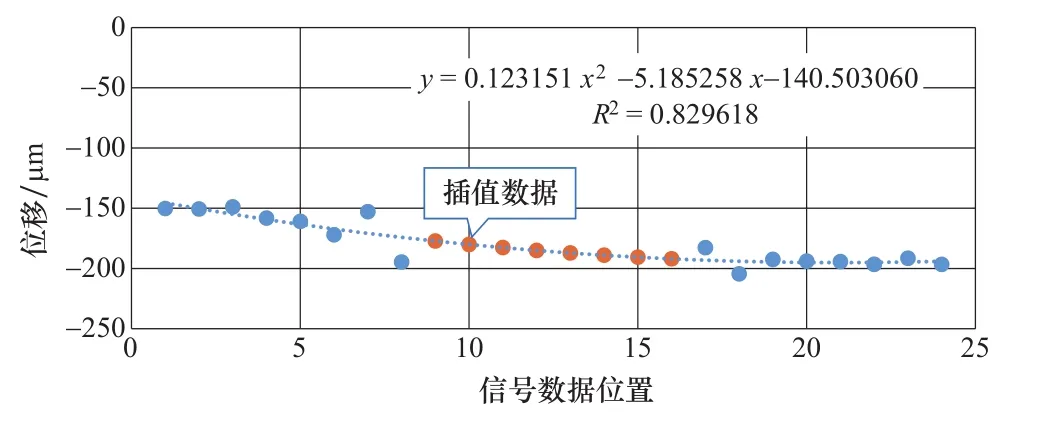
图7 信号数据二次多项式拟合结果Figure 7 Quadratic polynomial fitting results of signal pulse segment

3 应用示例

某抽水蓄能机组额定发电工况下上导摆度X向与Y向信号波形如图8所示，上导摆度信号中存在强烈的宽脉冲干扰，应用本文方法对上导摆度X向信号进行脉冲干扰滤除处理。

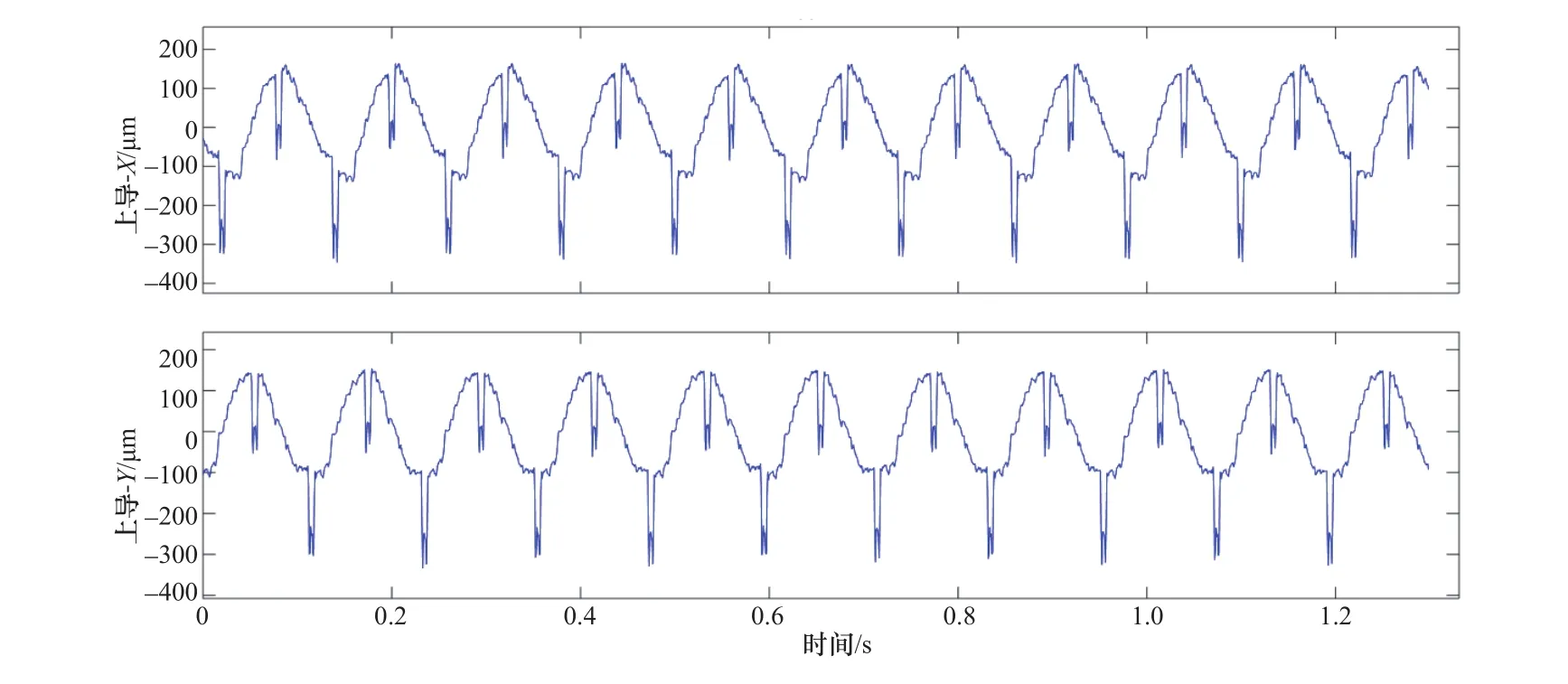
图8 某抽水蓄能机组上导摆度时域波形图Figure 8 Upper-guide bearing run-out waveform of a pumped storage unit

上导摆度X信号变化梯度序列曲线如图9所示；变化梯度序列数据概率密度分布如图10所示，采用93%置信度获得脉冲判断正阈值为50，负阈值为-48；脉冲结束位置相对脉冲起始位置数值变化幅度阈值设为15%，应用本文方法滤除强烈的宽脉冲干扰后的上导摆度X向信号变化曲线如图11所示，可见，强烈的宽脉冲干扰得到了有效滤除。原上导摆度X信号的频域幅值谱如图12所示，滤除脉冲干扰后的频域幅值谱图如图13所示，对比图12与图13可知，脉冲干扰导致信号在频域出现了较多虚假的频率成分，而采用本文方法滤除脉冲干扰后避免了这一现象。可见，采用本文方法可以获得准确的时域幅值和频域主要频率成分等特征参数，从而准确地掌握主轴摆度状况与评价机组的运行状态。

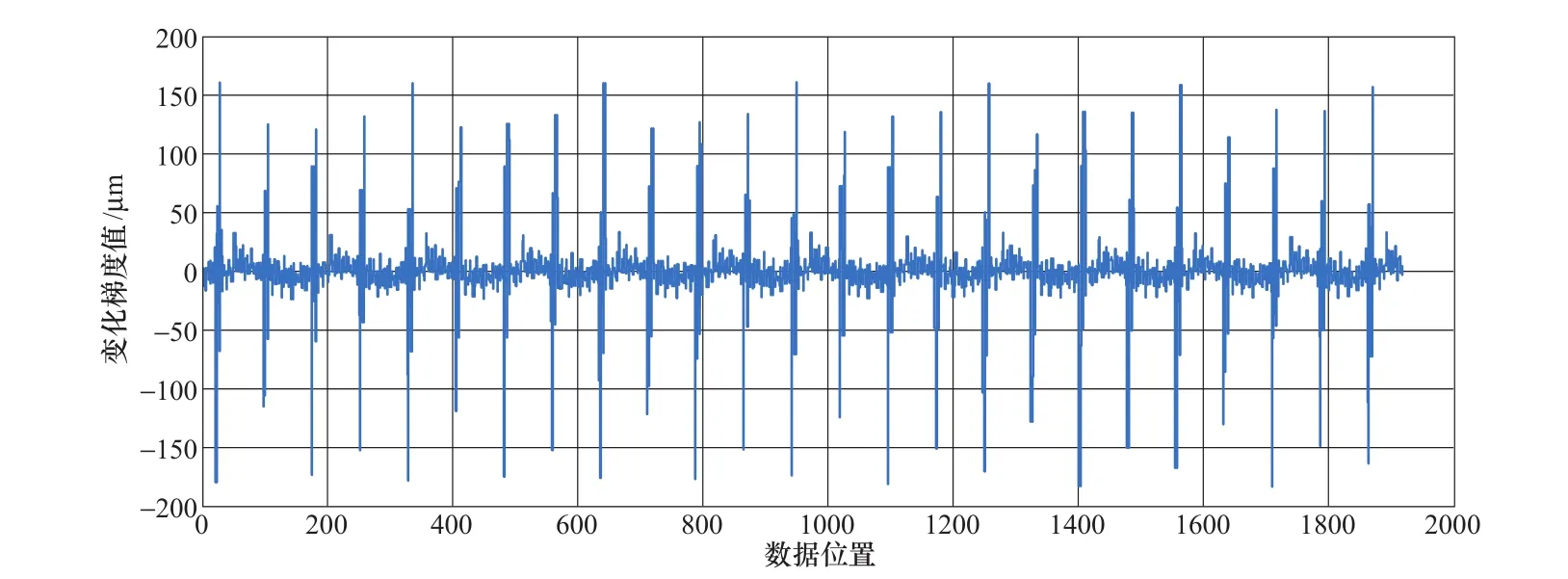
图9 上导摆度X信号变化梯度序列曲线Figure 9 Change gradient waveform of upper-guide bearing run-out in X direction

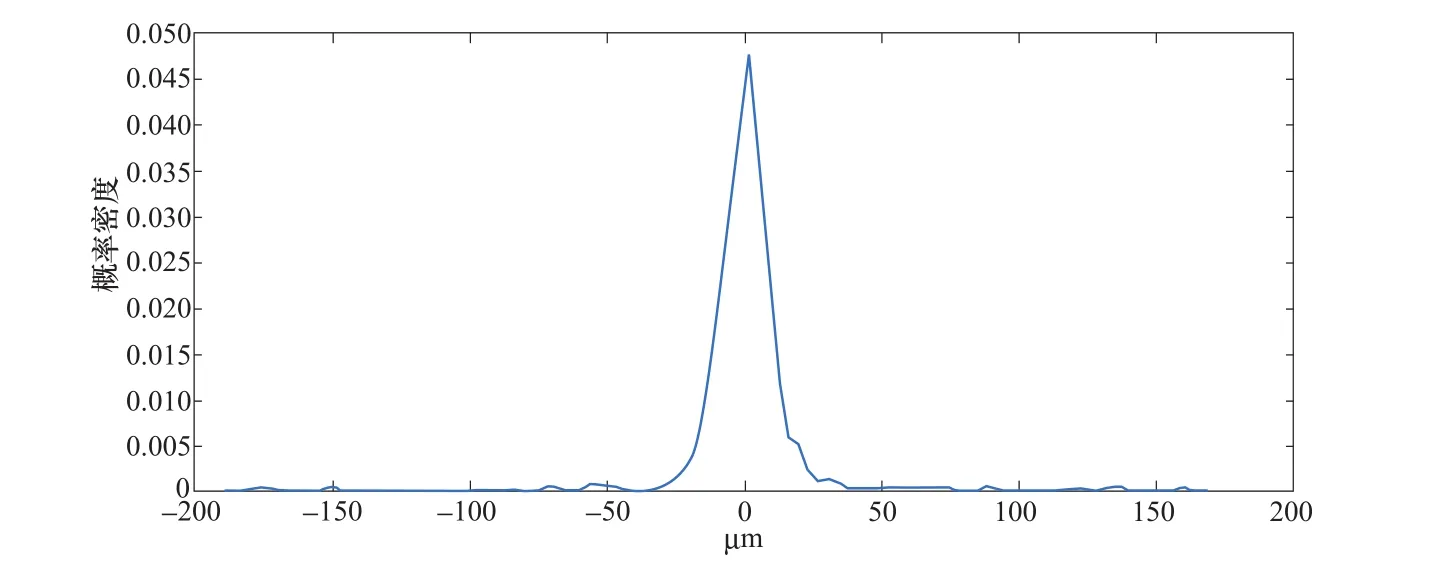
图10 变化梯度序列数据概率密度分布曲线Figure 10 Probability density distribution curve of change gradient sequence

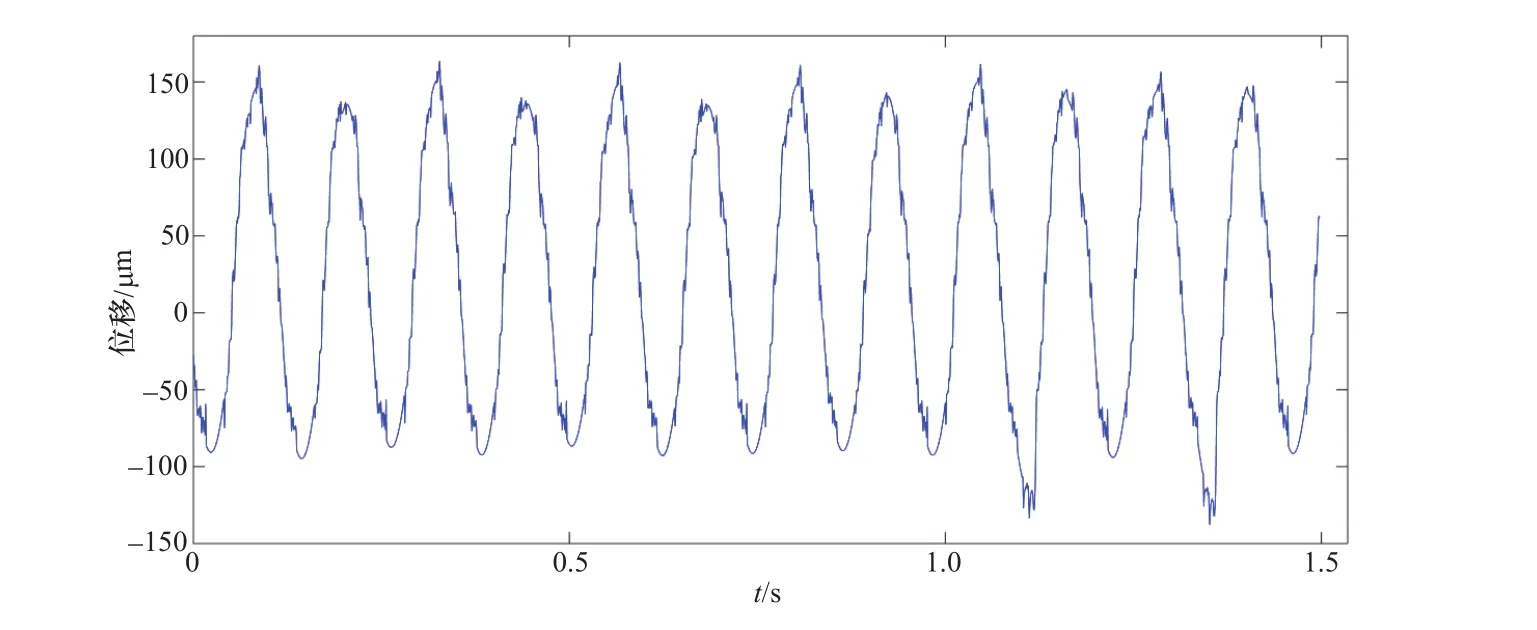
图11 上导摆度X信号滤除脉冲后波形曲线Figure 11 Waveform of upper guide bearing run-out in X direction after removing pulse interference

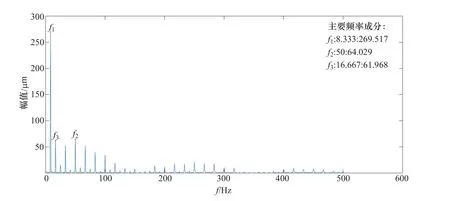
图12 上导摆度X信号未滤除脉冲的频域幅值谱图Figure 12 Amplitude spectrum of upper guide bearing run-out in X direction without removing pulse interference

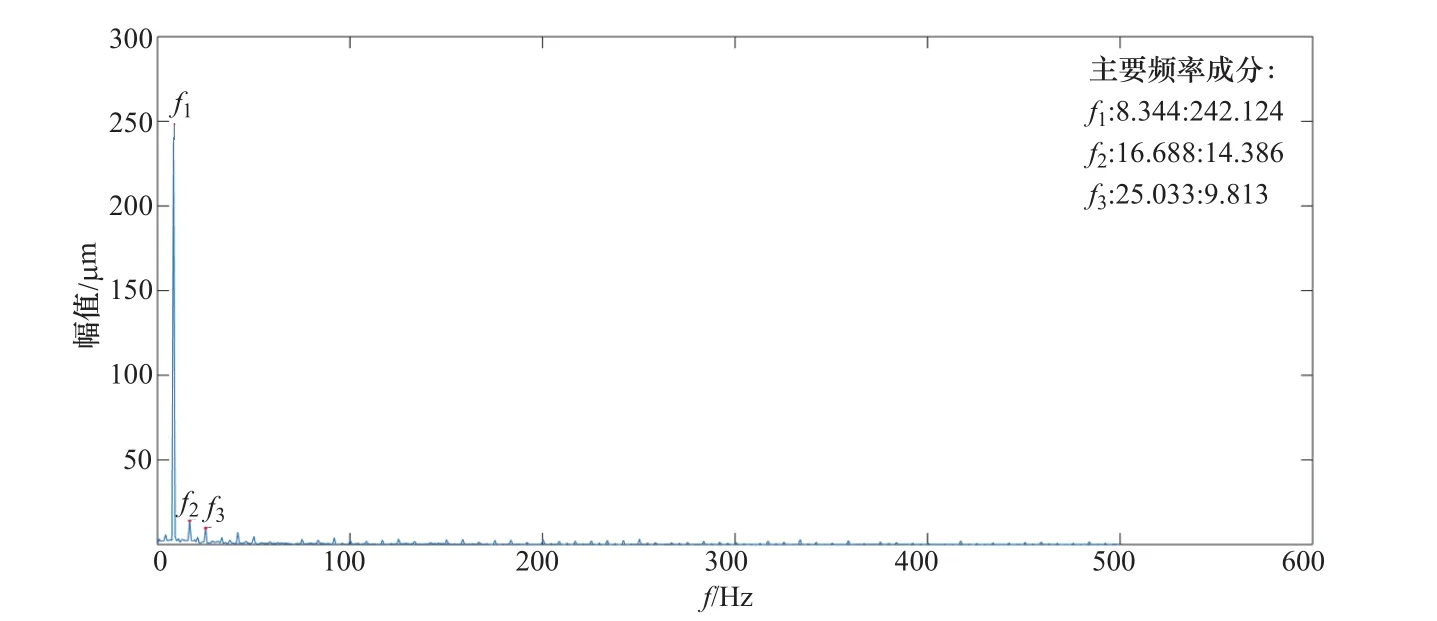
图13 上导摆度X信号滤除脉冲后的频域幅值谱图Figure 13 Amplitude spectrum of upper guide bearing run-out in X direction after removing pulse interference

4 结论

主轴摆度是衡量水电机组运行稳定性的重要指标之一，包含了丰富的机组运行信息。而实际测量得到的主轴摆度信号可能含有强烈的脉冲干扰，若不进行干扰脉冲滤除处理，则会得到偏大的主轴摆度幅值和虚假的频率成分信息，从而影响对机组运行状态的正确评价，甚至会影响机组出现非正常停机现象，给机组的安全稳定运行带来严重的负面影响。本文提出了一种滤除水电机组主轴摆度信号中脉冲干扰的方法，该方法可有效滤除脉冲干扰，从而获得准确的时域幅值和主要频率成分等特征参数，继而准确地了解主轴摆度状况与评价机组的运行状态。此外，该方法同时适用于窄脉冲和宽脉冲现象。