基于ABAQUS的地下式沉沙池结构内力有限元分析

彭兆轩，哈斯也提·热合曼，柳 莹

(1.新疆水利水电规划设计管理局，新疆 乌鲁木齐 830000;2.新疆水利水电科学研究院，新疆 乌鲁木齐 830000)

沉沙池常用于水利工程和污水处理工程，主要目的是对水中的沙预先沉降分离，除去水中粒径大于0.2mm且密度大于2.65t/m3沙砾，在一定程度上避免水中的沙石颗粒磨损水轮机、机泵、堵塞管道等。目前使用最多的沉沙池主要分为平流沉沙池、曝气沉沙池和旋流沉沙池等，不同的沉沙池对于不同粒径范围的沙粒，其除沙效果是不同的[1-2]。李凯等人提出了单室沉沙池池长的计算方法，在满足平均流速的前提下，根据池内水深和池宽的组合推求最小池长[3]。刘增强等人根据厄瓜多尔CCS水电站沉沙池引水量大、工程规模大、泥沙含量大的特点，采用BIM技术模拟沉沙池的施工全过程[4]。葛占军根据山西中部引黄工程中具有高陡边坡且局部倒悬的沉沙池为例，研究并分析了施工网的布设及边坡的开挖[5]。孟俊达等人采用数值模型和物理模型相结合的方式，对重力沉沙池的各项结构参数进一步优化，并分析了不同侧堰长度和位置对重力沉沙池水沙分离效率的影响[6]。目前不少学者对地上式沉沙池的结构参数、水沙分离效率及沉沙池施工过程进行了较多的分析研究，然而对地下式大断面、大开挖的沉沙池支护和衬砌的内力研究较少。地下式沉沙池与隧洞均属于地下洞室结构，其内力计算方法与隧洞类似但又不完全一样，当前隧洞结构计算大都采用有限元法、边值法及改进的边值法，其中改进的边值法计算结果较为符合工程实际[7-10]。

1 计算原理与方法

目前，对于隧洞衬砌的内力计算主要采用两种计算模型，第一种是以衬砌结构作为承载主体，围岩作为载荷的主要来源，同时考虑其对衬砌位移的约束，采用径向弹簧和切向弹簧模拟衬砌与围岩之间的接触作用，这种模型为载荷-结构计算模型；第二种计算模型则相反，以围岩作为承载主体，衬砌结构对围岩的位移起到一定的约束作用，这种模型为地层-结构计算模型。载荷-结构计算模型适用于围岩因过分变形而发生松弛和崩塌且衬砌结构主动承担围岩松动压力的情况，而地层-结构计算模型将衬砌结构与围岩视为一个整体，作为共同承载的隧洞结构体系。一般情况下，载荷-结构法计算结果较地层-结构法大。

围岩压力根据SL 744—2016《水工建筑物荷载设计规范》计算，其中竖向围岩压力计算公式为：

qv=(0.2～0.3)γRB

式中，qv—竖向围岩压力，kPa；γR—岩体容重，kN/m3；B—洞室开挖跨度，m。

围岩侧压力计算公式为：

qh=(0.05～0.1)γRH

式中，qh—围岩侧压力，kPa；H—洞室开挖高度，m。

径向和切向弹簧刚度计算公式为：

Kr=Erbθ/(1+Vr)

Kt=KrG/Er=05Kr/(1+Vr)

式中，Kr—径向弹簧刚度，N/m;Kt—切向弹簧刚度，N/m;Er—变形模量，Pa;G—剪切模量，Pa;θ—相邻弹簧夹角弧度值，rad;b—隧洞宽度，m;Vr—围岩泊松比。

2 工程实例分析

2.1 工程概况

某坝为碾压式混凝土坝，坝顶全长62m，左侧布置两道泄洪冲沙闸，弧形闸门(宽4m×高4.5m)，滑动平板闸门(1m×1m)。右侧为溢流坝段，坝顶高程1833.0m，坝高11m，坝顶长40m，采用消能戽消能。坝体两侧翼墙顶部高程1836.5m，左岸长40m，右岸长36m，1000年一遇设计洪水位1836.07m。河岸处取水口宽6.4m，高4.0m，设计底高程1822m，从取水口到沉沙池的连接渠道长约80m，地下沉沙池设计断面120m2，总长100m，分为左右两个腔室，设计底高程1817～1821m，坡度为4%。地下沉沙池围岩类型为Ⅲ类，主要为变质沉积岩，中等-强风化，节理中等-密集发育。根据地震动参数区划图，工程区的峰值加速度为0.32g。

2.2 计算模型

地下沉沙池围岩类型为Ⅲ类，由于考虑到锚杆以及预应力锚索的作用，将支护-锚杆-预应力锚索-围岩视为一个整体，因此采用有限元方法(地层-结构法)可更真实的模拟锚杆、预应力锚索与支护之间的相互作用，如图1所示。模型计算范围取8倍的洞径，围岩采用实体单元模拟，支护采用梁单元模拟，锚杆和预应力锚索采用杆单元模拟，左右围岩边界水平向约束(即滚轴支座)，底边固定约束(即固定支座)。为真实有效的模拟沉沙池开挖过程，采用软化模量法，在支护和衬砌施工前，先将待开挖区单元的模量降低40%，以此来模拟应力释放效应。

图1 支护应力应变计算模型(地层-结构法)

结合本工程围岩类型及裂隙发育程度，出于保守和安全可靠性考虑，衬砌结构内力计算采用载荷-结构法，利用径向弹簧和切向弹簧模拟衬砌与围岩之间的接触作用，对不与衬砌相连的弹簧节点水平、竖直方向进行自由度约束。在对衬砌施加围岩压力、水压力及自重等荷载后，将会产生一定的变形，导致一部分弹簧受拉，一部分弹簧受压。若径向弹簧受拉，此时围岩与衬砌之间没有摩擦力，则相应的切向弹簧和径向弹簧也应一同被钝化，计算模型如图2所示。

图2 衬砌应力应变计算模型(载荷-结构法)

计算模型均采用笛卡尔直角坐标系，y轴方向为竖直向，x轴方向为水平向。地层结构法计算模型共分为7878个节点和7802个单元，荷载结构法共分为64个节点和128个弹簧单元。

2.3 计算工况

本次计算工况分为单侧过水工况、无水运行工况及地震工况，每种工况的荷载组合系数见表1。在计算地震工况时，采用拟静力法计算岩石荷载、结构自重以及裂隙水的地震惯性力，抗震设计荷载组合取决于结构构件的性能要求。

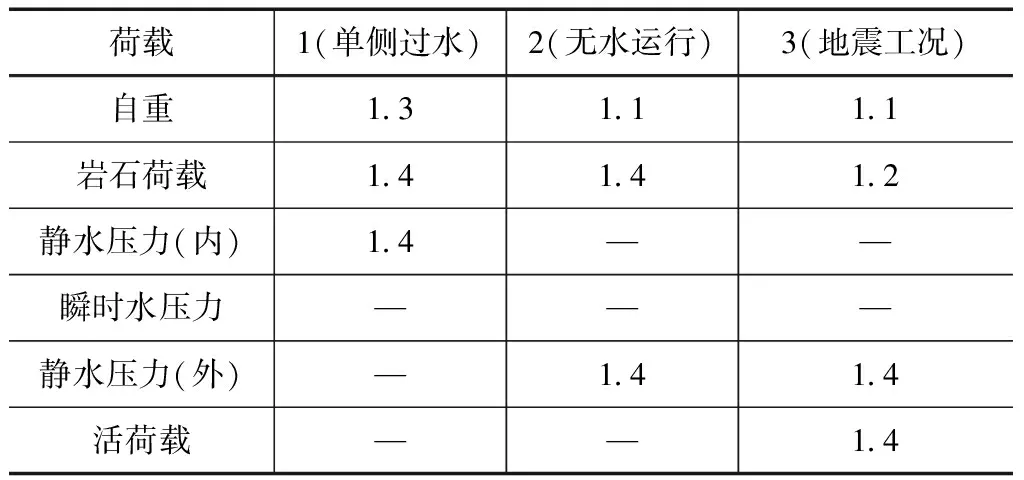
表1 沉沙池计算工况及推荐荷载系数

2.4 计算假定与材料参数

在进行地下式沉沙池计算时，通常做如下基本假定：材料的密度、弹性模量、泊松比为各向同性；围岩按摩尔库伦本构模型考虑，支护、衬砌按线弹性模型考虑；初始应力场仅考虑自重作用；不考虑地下水在开挖过程中的作用。各材料参数见表2。

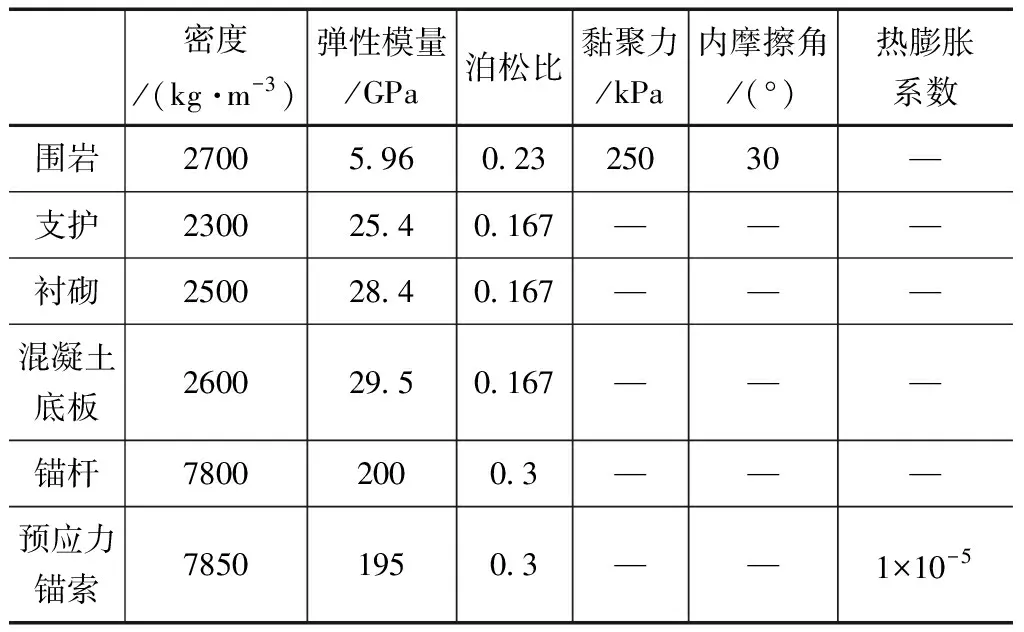
表2 沉沙池材料参数表

3 计算结果与分析

3.1 支护位移与内力

支护的位移及内力计算结合施工图，真实模拟地下洞室施工过程，共分为16步依次开挖，通过地层-结构法分析支护结构的应力应变，开挖完成后支护水平位移和竖向位移如图3—4所示，轴力和弯矩如图5—6所示。

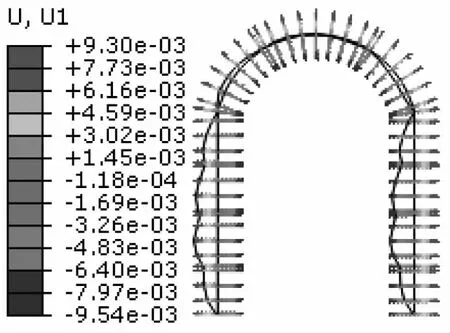
图3 支护水平位移分布图(单位：m)

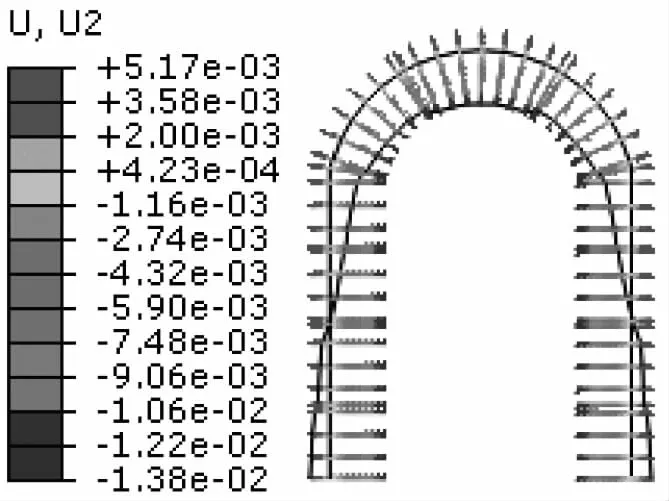
图4 支护竖向位移分布图(单位：m)

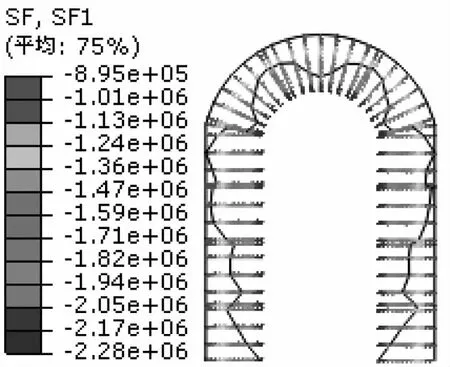
图5 支护轴力分布图(单位：m)

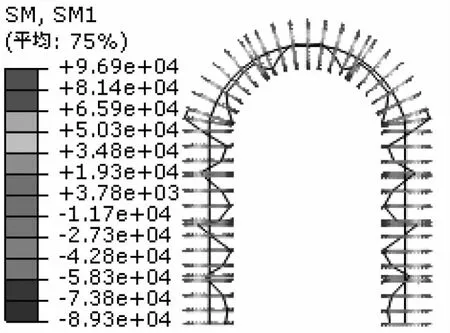
图6 支护弯矩分布图(单位：m)

从图3—4中可以看出，水平位移左右对称，但方向相反，竖向位移从顶拱至侧墙底部逐渐减小。这是因为在围岩侧压力作用下，支护左右侧壁分别向洞内变形，最大值为9.54mm；在竖向围岩压力作用下，支护顶拱承担了绝大部分压力并向左右侧墙传导，因此顶拱中部最大竖向位移达13.8mm，两侧端墙底部因地基隆起，有略微向上发生变形的趋势。支护的轴力和弯矩是反映结构是否安全的重要指标。从图5—6中可以明显的看出轴力和弯矩关于中轴线左右对称，整个支护结构处于受压状态，最大轴力出现在侧墙底部，最大值为2.28×106N；弯矩最大值出现在顶拱和侧墙交接部位，最大值为9.69×104N·m，而顶拱中间部位弯矩最小。

锚杆和预应力锚索的轴力分布如图7所示。锚杆最大轴力为1.20×105N，预应力锚索长20m，间距1.2m，最大轴力为4.64×105N。根据锚杆和预应力锚索的受力情况可知，预应力锚索对加强支护稳定起到了关键性的作用。

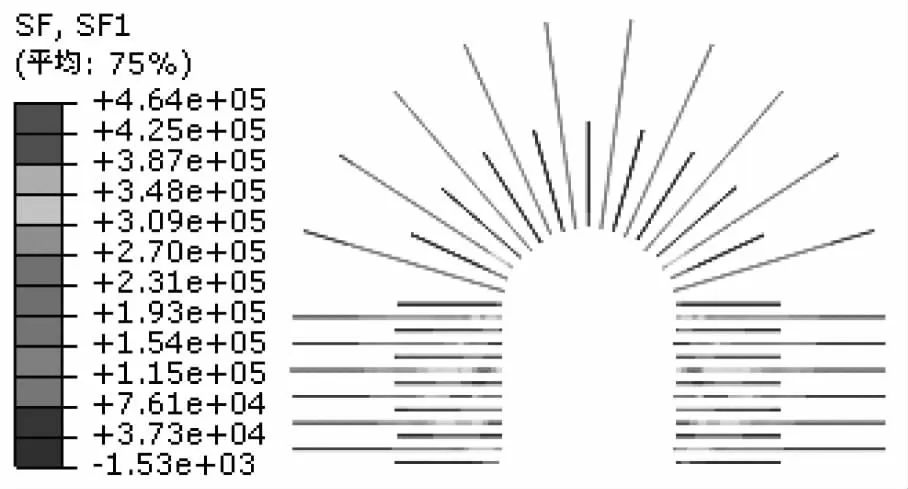
图7 锚杆和预应力锚索的轴力分布图

3.2 衬砌内力计算与分析

衬砌相对支护而言，是在隧洞已经进行初期支护的条件下，用混凝土、钢筋等材料修建的内层结构，在防止围岩变形或坍塌方面起到了关键作用。采用载荷-结构法进行计算，利用土弹簧模拟围岩与衬砌之间的相互作用，计算3种工况下衬砌结构的内力大小，从而进一步分析结构的安全性。根据各个工况下衬砌轴力和弯矩分布图，通过比较分析选择了A、B、C、D、E、F、G、H、I共9个典型节点，节点编号依次为90号、79号、10号、17号、113号、121号、61号、39号、23号。3个不同工况下衬砌结构的轴力和弯矩分布图如图8—13所示。

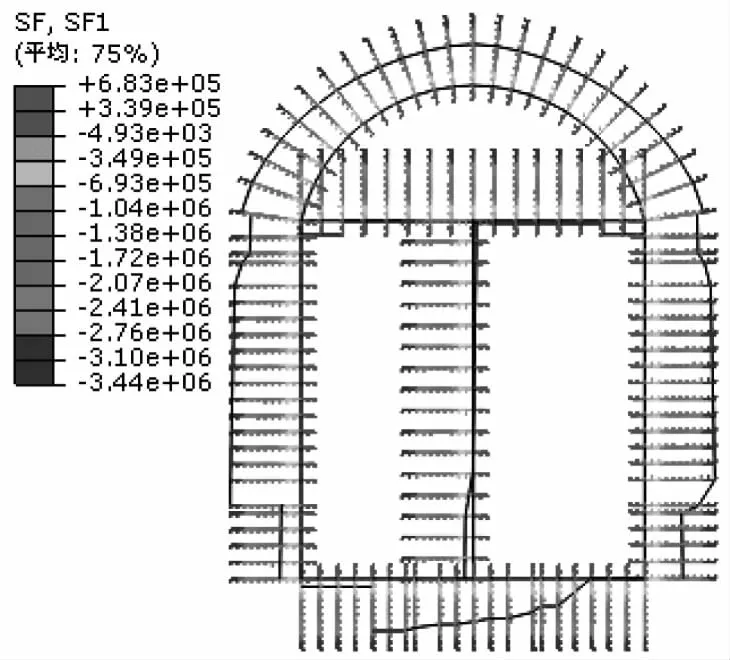
图8 衬砌轴力分布图(工况1，单位：N)

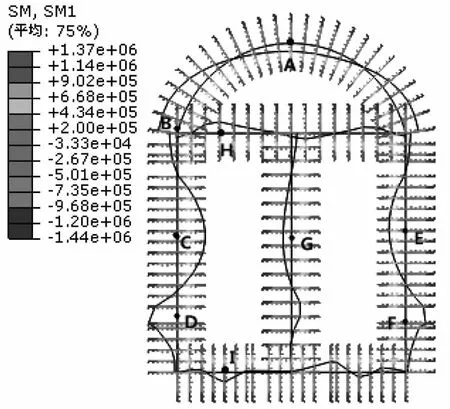
图9 衬砌弯矩分布图(工况1，单位：N·m)

单侧过水工况下衬砌结构的轴力和弯矩如图8—9所示。衬砌结构内部中间隔墙和上部横梁所受的轴力最小，而左右侧墙承受的轴力较大，最大值可达3.44×106N。单侧过水对结构的轴力影响较小，但对结构的弯矩影响显著，因沉沙池右侧过水而左侧无水，在水压力的作用下，中间隔墙产生了较大弯矩；与此同时，水压力也可抵消右侧墙承受的部分水平向围岩压力，所以E点弯矩较C点小，弯矩最大值出现在左侧墙中部C点，大小为1.44×105N·m。

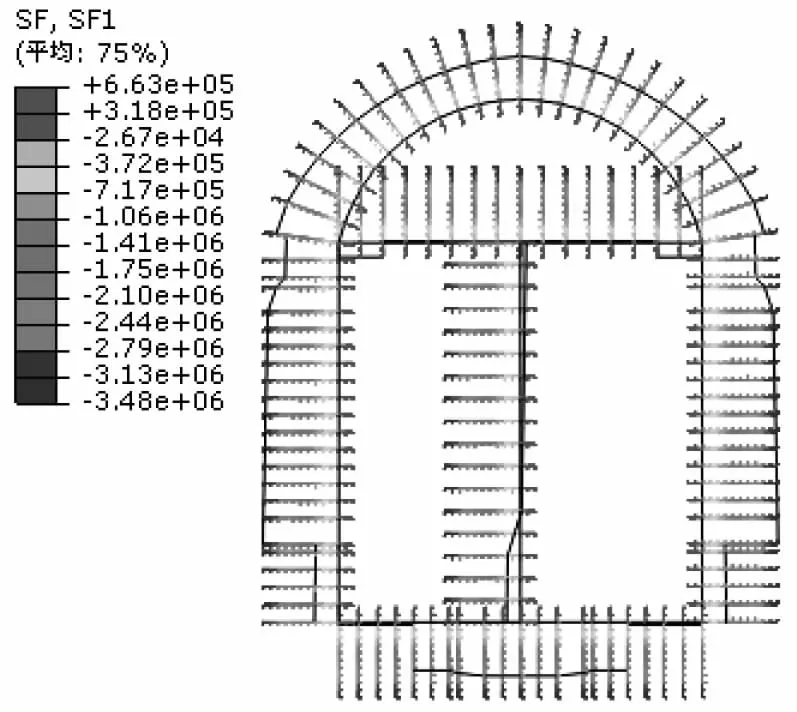
图10 衬砌轴力分布图(工况2)

地震工况下衬砌结构的轴力和弯矩如图12—13所示。沉沙池结构的正常运行工况为单侧过水，因此本次地震工况是在单侧过水的情况下叠加计算完成的。轴力分布情况与工况一、工况二类似，轴力最大值为4.05×106N，出现在左侧墙距底部1/5处的D点，中间隔墙与上部横梁的轴力最小。在地震惯性力的作用下，弯矩最大值出现在右侧墙中部的E点，最大值为1.4×106N·m，因部分地震惯性力与左侧围岩压力部分抵消，使得弯矩值较右侧小。

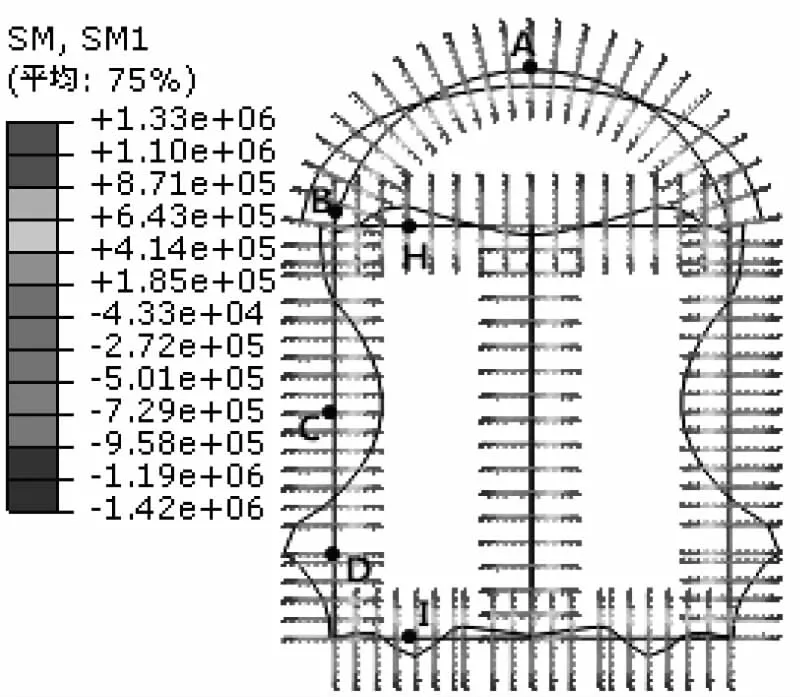
图11 衬砌弯矩分布图(工况2)

无水工况下衬砌结构的轴力和弯矩如图10—11所示。轴力分布图关于中轴线左右对称，轴力最大值为3.48×106N，出现在左右侧墙距底部1/5处的D点，中间隔墙和上部横梁的轴力最小，分布特点及大小与工况一类似。弯矩分布图也是关于中轴线左右对称，最大值为1.42×106N·m，出现的位置与轴力最大值所处位置相同，因沉沙池左右腔室均无水，所以中间隔墙的弯矩为0。

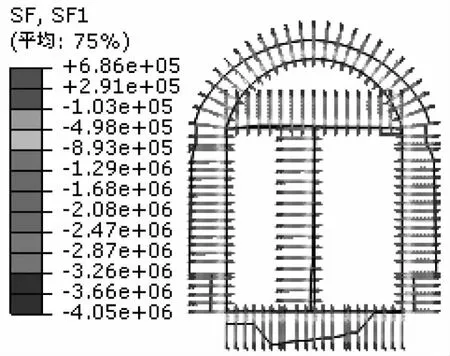
图12 衬砌轴力分布图(工况3)

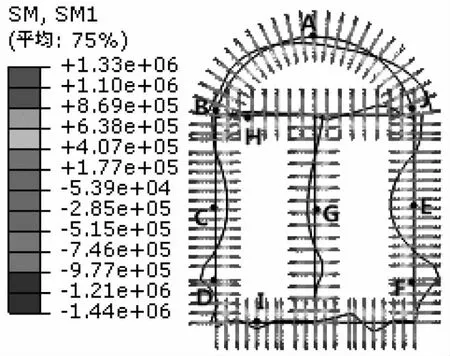
图13 衬砌弯矩分布图(工况3)

通过上述分析可清楚的了解到衬砌轴力和弯矩的分布规律及最大值出现的位置，但不便直观的研究3种工况下衬砌轴力和弯矩的变化趋势。因此，根据9个典型节点的内力大小，绘制衬砌结构的轴力和弯矩变化趋势，如图14—15所示。

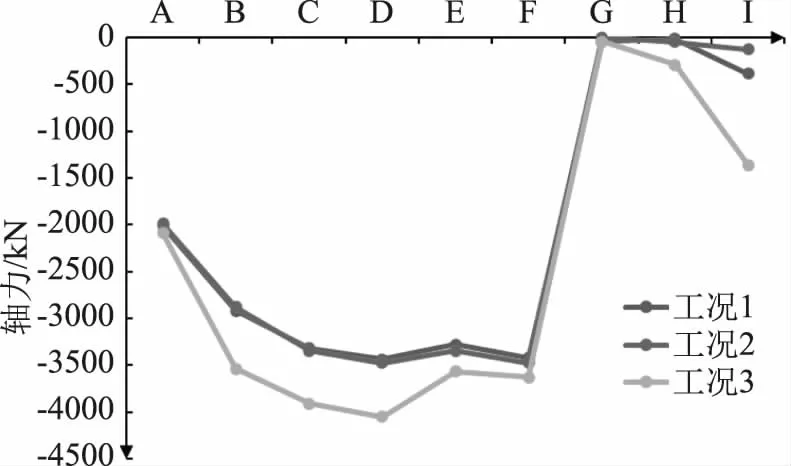
图14 衬砌结构轴力变化趋势图

图15 衬砌结构弯矩变化趋势图

根据衬砌结构的轴力和弯矩变化趋势图可知，3种工况的轴力和弯矩变化规律基本一致，中间隔墙、上部横梁和底板处的轴力弯矩最小，地震工况下的轴力稍大于单侧过水工况和无水工况。3种工况下，D点的弯矩分别为1.44×106、1.42×106、9.31×105N·m，E点的弯矩分别为8.29×105、1.37×106、1.30×106N·m，不难看出，单侧放水工况下衬砌弯矩值较地震工况大。这是因为地震工况下衬砌受力虽然较单侧过水工况大，但地震工况荷载组合系数较低，特别是岩石荷载系数由1.4降至1.2。通过上述分析，单侧过水工况是衬砌结构的控制工况。

4 结语

本文通过大型通用有限元软件ABAQUS对地下式沉沙池在3种工况下进行了内力计算分析，单侧过水工况为控制工况，支护顶拱中部变形较大，衬砌左侧边墙距底部1/5处的轴力和弯矩均达到最大值，轴力以压应力为主，对混凝土结构影响不大，然而过大的弯矩将会导致结构表面出现裂缝、渗水，甚至容易造成断裂的危险。因此，通过分析比较，地下式沉沙池支护和衬砌结构基本满足稳定要求，但建议对顶拱部位的围岩采取固结灌浆，对衬砌左右侧边墙底部薄弱部位的配筋计算进一步优化。