地下水资源模型的模糊评价分析

崔文臣

（招远市玲珑镇人民政府，山东 招远 265406）

地球上的淡水资源量在全部水资源量中占比约为2.53%，淡水资源中68.7%为不可利用的极地与高原冰川，可利用的水资源约占全部水资源0.79%，随着全球工业化进程快速推进，主要经济体对淡水资源的需求量与日俱增，淡水资源指标成为评价区域发展力的重要指标[1]。为了解决区域经济发展过程中快速增长的淡水资源需求与相对短缺的淡水资源储量之间的矛盾，设计一种水资源评价模型，可以从区域可用水资源的储量、开采能力、补给能力等多方面给出模糊权重分析[2]。

基于地下水上覆土层岩层结构影响评价过程中对地下水资源的直接观察，且第四系中的浅层地下水和理论最深可达数千米的深层地下水的评价方式不同，浅层地下水可根据钻孔物探法进行评价，深层地下水必须采用回声物探或地电阻物探等其他物探法进行评价，对综合物探方法得到的相关数据进行整合分析，成为当前地下水资源（储量、开采能力、补给能力）评价模型的重要研究课题[3]。

该研究重点针对不同物探方法获得的数据集设计一种模糊权重模型，排除以往可采地下水与不可采地下水的分别评价方法，实现对区域地下水资源的全面客观评价（包括储量、开采能力、补给能力）[4]。

1 地下水资源的一般模式

除第四系浅层地下水外，地下水一般分为孔隙水、裂隙水和岩溶水，当前技术条件下，位于砂岩、砾岩中的孔隙水和位于石灰岩、白云岩中的岩溶水是得到较为广泛开采利用的深层地下水，裂隙水因为分布条件较为复杂，只在少数极端缺水地区进行开采，多作为浅层水、孔隙水、岩溶水的交叉补给通道[5]。地下水的一般赋存模式，如图1所示。

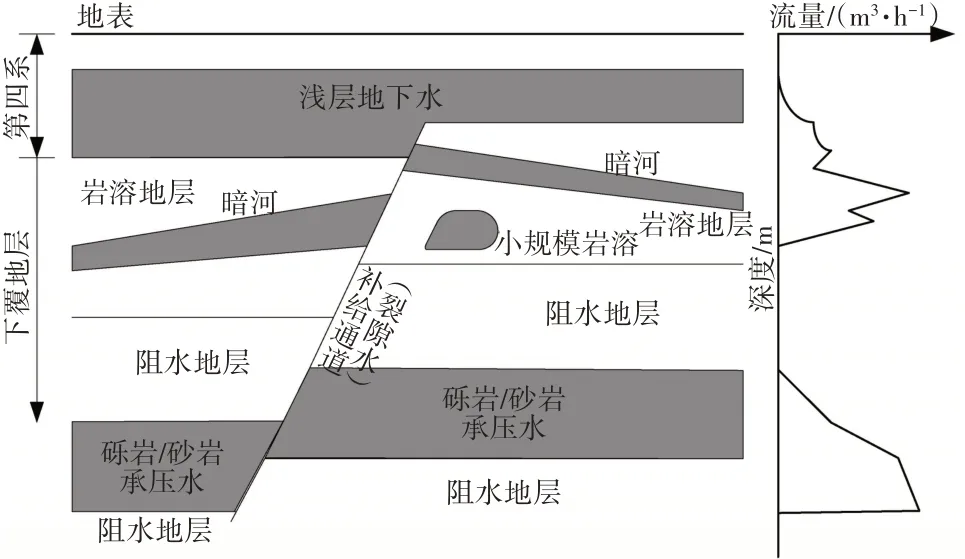
图1 地下水一般赋存模式

图1中，除极端干旱地区外，绝大多数第四系发育地区，均会在第四系地层下部形成浅层地下水，这部分地下水是地表植被的根系发育区域。早期人类对地下水的开发过程，也主要是对浅层地下水的开采过程。具有岩溶地层的区域，岩溶地层本身具有一定的阻水特性，但其可溶性容易形成暗河和岩溶湖等小规模岩溶结构[6]。中国西南地区等因地下水埋深较大产生的缺水地区，重点在于对岩溶水的开采过程。而砾岩、砂岩、白云岩等产生的承压水可能沿补给通道上行，在地表形成承压泉[7]。

通过对上述地下水赋存模式的调查，可以形成基于地理信息系统（Geographic Information System，GIS）坐标系网格的地下水储量及深度分布数据，但此数据并不能直接对区域经济发展赋能[8]。而需要考察区域地下水开发体系，即分析该区域内的地下水开采利用能力，近期可实现的地下水开采能力、中远期地下水开采规划，地下水循环过程中地下水的补给能力[9]。所以，本文给出的评价模型中，地下水储量（可利用、预期可采、远期可用、不可采）因子、地下水开采能力因子、地下水补给能力因子等共同构成了当地地下水资源的评价指标[10]。

2 地下水资源模型因子设计

2.1 地下水储量因子

地下水储量资源，包括其可利用储量、预期可采储量、远期可用储量、不可采储量等，均可利用现有的物探手段得到详细数据[11]。在地下水物探中，采用遥感法、钻孔法、回声法、地震法、地电阻法等均可以提供数据，但数据之间存在互补[12]。所有方法最终得到的数据均是在GIS 地理信息坐标点上不同埋深条件下的储量数据，可以构建一个类模型，计算式为：

式中：Gh(x,y,h)为特定GIS 坐标(x,y)上，特定深度h的地下水赋存情况；积分区域为最大测量深度H到地表h=0 区域；P(h)为特定深度h上的地下水资源经济赋能能力转化系数；G(x,y)为特定GIS坐标(x,y)上的地下水水位实测值。

其中，地下水资源经济赋能能力转化系数P(h)一般为线性倒数函数，因为地下水埋深越大，其开采难度越大，表达式为：

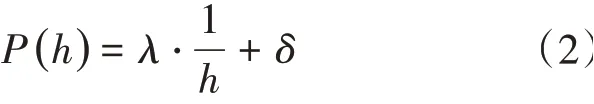
式中：h为地下水资源埋深；λ,δ分别为该转化函数的斜率调整因子和截距调整因子，其赋值从当地当时地下水开采工程概算过程中可以列出回归模型进而计算获得[13，14]。

2.2 地下水补给能力因子

在勘探区域内布置抽水探井且调查区域内的工作水井，根据其抽水量m以及对应抽水量m条件下的地下水水位变化情况Δh(m)，可以推测计算该区域内的地下水补给能力，同时观察该区域内的浅水水位变化趋势Δh(t) ，判断该区域内地下水宏观补给情况。因为新中国成立以后各地水文、国土部门均在持续观察各地浅层地下水赋存状态变化情况，该部分数据较为丰富，可以实现对该模型的有效数据支持。

利用线性平均法，将已知测点数据向GIS 坐标(x,y)上进行分摊，得到最终的地下水补给能力因子计算式为：

式中：M(x,y)为特定GIS 坐标(x,y)上地下水补给能力的评价值；N为调查的宏观地下水水位变化时间周期；其余变量含义同前文所述。

2.3 地下水开采能力因子

设地下水开采能力在特定GIS坐标(x,y) 上的表现为T(x,y) ，当开采能力T超过补给能力M时，会使M评价结果大幅度下降，造成地下水资源环境不断恶化，而当开采能力T小于补给能力M时，会造成地下水资源对当地经济发展的赋能能力不足。所以，可以单独考察该地下水开采能力因子，在后续模糊权重整合中，该地下水开采能力因子T(x,y) 和前文设计的地下水补给能力因子M(x,y) 的任何一方获得较低评价得分，均可传导给最终评价因子。该过程可以使评价过程得到简化，且不影响当地地下水评估结果的客观表达。

各地已经建成的地下水开采设施，包括中浅层机井、深层水源井等，因为当前技术条件的制约，其数量较小，分布不均，但也可以通过分摊算法将开采量分摊到特定GIS 坐标(x,y)上形成T(x,y)，此处不展开论述地下水开采能力因子的计算过程，下文分析研究中会直接调用该因子。

3 地下水资源模型模糊权重整合模式设计

传统的模糊控制矩阵算法，是在发生值与环比差值中划分值域分段，根据两两交叉的方式，基于数据落点采用不同策略进行数据处理。但模糊权重模型是在2 个或者多个控制因子之间形成交叉策略，在权重因子的控制下，实现受多因子影响的控制结果输出。

前文公式（1）（2）（3）标定的地下水资源模型的控制因子共有3 个，分别为地下水储量因子G(x,y) 、地下水补给能力因子M(x,y) 、地下水开采能力因子T(x,y)，这3 个控制因子均为分摊到GIS 特定坐标(x,y)上的表达因子，且地下水补给能力因子M(x,y)已经考虑到地下水储量的变化，所以该模糊权重整合模式无须继续整合其变化量指标即可实现对地下水变化量的评价。地下水开采能力因子T(x,y)直接影响到区域经济的资源赋能过程，而地下水补给能力因子M(x,y)关系到地下水开采的可持续性，而地下水储量因子同时作用于地下水开采能力因子T(x,y)和地下水补给能力因子M(x,y)，其逻辑关系如图2所示。

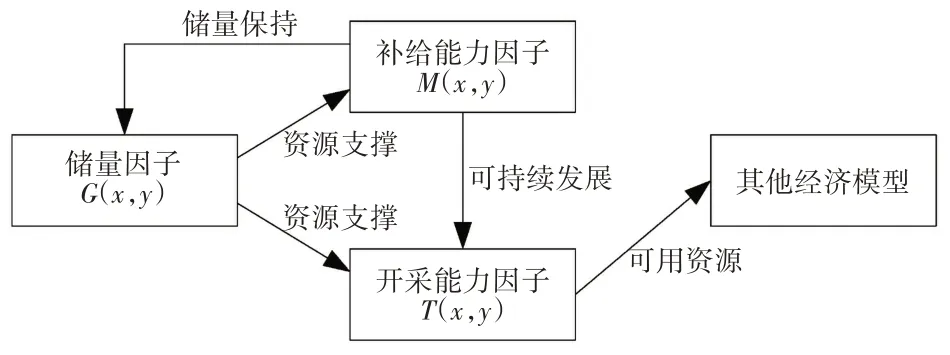
图2 因子逻辑关系

由图2 可知，开采能力因子解决了地方经济发展中维持经济发展所需的不断增加的资源需求与有限资源供给能力的矛盾，属于主要矛盾；而储量因子和补给能力因子解决了持续增长的资源开采量与资源地质储量的矛盾，属于次要矛盾。因此，该研究中开采能力因子给与50%权重，补给能力因子给与35%权重，储量因子给与15%权重。

此时如果直接利用模糊权重乘积法进行数据整合，因为3个因子的数据来源不同，不同量纲导致其值域范围不同，其数据本身也会给权重带来影响。所以，需要对上述3个因子进行线性重投影（min-max算法），其计算公式为：

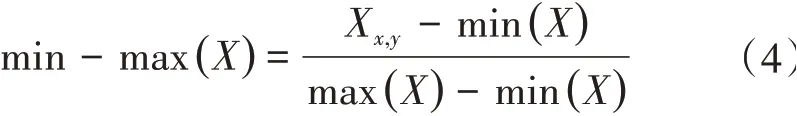
式中：Xx,y为特定因子矩阵中GIS 坐标(x,y)上的表达值；min(X),max(X)分别为该矩阵的整体最小值和整体最大值。针对上述3 个因子，分别独立进行式中的min-max 转换，使其所有发生值的投影区间分布到[0，1]区间上，且其最大值均为1.000、最小值均为0.000。

在此基础上，进行模糊权重乘法计算：

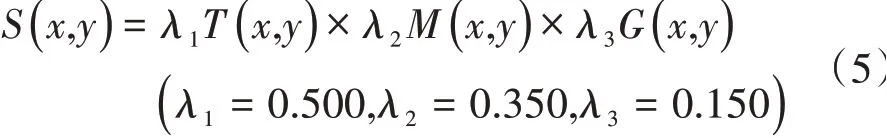
经过式（5）的计算，因为3个权重因子λ1+λ2+λ3= 1，且3个评价因子经过式（4）的重投影计算后，其值域范围均在[0，1]区间上，如此相乘后，其最终值域范围不超出[0，1]区间，但大概率小于[0，1]区间，为了充分保障最终数据结果的可用性，该输出矩阵S(x,y) 需要根据式（4）再进行一次min-max 变换，使其结果工整投影到[0，1]区间上，以方便评价数据的后续应用。

4 设计模型的应用场景及应用效果

4.1 地区差异性在该应用场景中的表达

由上述分析不难发现，如果使用该模型对多个不同地区进行分析，其最终评价结果会出现极端缺水的南疆、桂南地区和洪涝灾害显著的长江、珠江中下游地区评价结果基本一致。因此，该模型仅可实现对调差区域内的地下水分布情况差异性做出评价，无法实现跨区域的地下水分布情况评价。也就是说，单独使用该模型进行区域地下水评价中，仅能支持对同区域地下水开发规划的数据支持。

所以，在相关应用中，若要进行多地区地下水资源比较，则需要在前文第一次min-max转化时，将多个同时考察地区的数据进行统一min-max 转化，即该模型需要对不同区域的地下水储量、补给能力、开采能力的数据进行统一分析。

4.2 数据仿真结果对模型计算效能的验证

考察广西百色、内蒙古赤峰、新疆和田、江苏南京、山东青岛5 个地下水赋存特征有较显著差异的城市，在统一规划min-max 数据整合区域的前提下使用该模型对其地下水评价指标进行分析，得到结果如图3所示。

图3 城市统一评价结果比较

由图3 可知，传统观念中青岛与赤峰属于中度缺水城市，和田与百色属于重度缺水城市，将5个城市的GIS 数据利用该模型进行汇总评价计算后，发现5 个城市表现出较大的差异性。如，和田地区自新中国成立以来的大规模坎儿井地下水汇集工程建设成果在该模型中得到体现，百色地区对岩溶水的开发工程也被充分体现出来，这2 个地区均表现出开采能力超越储量和补给能力的情况。和田地区的地下水开发过程与储量人工优化工程也使储量数据差异性得到一定程度表达。而青岛海绵城市的特征使储量远大于补给能力，且开采能力远大于储量。赤峰也表现出类似特征，但不如青岛显著。而南京因为地表径流水资源充足，当前并无地下水开采计划，所以其地下水开采能力给出0.000的评价结果，但地下水储量和补给能力表现出1.000的最高结果。

如前文在城际数据比较中，该模型表现出较强的敏感性，体现出不同城市的地下水资源赋存状态和地下水资源开发状态。如将其应用于城域数据比较，可以对城市规划提出指导性数据支持。即该模型的主要应用场景是对城市地下水资源的赋存和利用状态做出基于GIS 地理信息坐标系的整合评价，供城市整体规划和经济评价过程参考。

5 结语

该模型在3 个控制性因子的设计中，采用了不同的数学方法，包括沿深度坐标轴或时间坐标轴的线性积分计算、均值计算、差值计算等，进而通过2次min-max 重投影计算，统一不同因子的值域和量纲，再利用模糊权重乘积法，得到最终评价结果。实际数据仿真结果中，该模型可以根据GIS 地理信息数据对不同区域的数据做出高敏感性测算，最终给出不同区域在地下水储量、地下水补给能力、地下水开采能力方面的整体评价。该数据可以作为城市规划和其他经济地理评价过程的支持数据。