基于灰色关联度样本优化的高速列车轴箱轴承温度预测方法
2022-07-15潘彦龙,胥如迅,2,3
潘 彦 龙,胥 如 迅,2,3
(1 兰州交通大学 机电技术研究所,兰州 730070;2 甘肃省物流及运输装备信息化工程技术研究中心,兰州 730070;3 甘肃省物流与运输装备行业技术中心,兰州 730070)
轴承是走行部旋转件的重要组成部分,其运行状态关乎列车安全运行。现阶段主要通地过安装在旋转件上的振动、温度传感器对列车走行部的轴承状态进行监测[1]。在列车运行过程中出现异常温升,暗示着列车轴承可能出现较严重的故障,而轴承的故障将导致列车的传动系统出现问题,进一步引起重大安全事故,因而异常温升是铁路部门极力避免出现的故障[2]。轴温异常升高的原因是多重因素共同作用的结果,但对于建模来说,将涉及到的因素都考虑在内,难免会影响模型的响应速度跟模型的精度,考虑因素过少则会降低模型的精度。因而对影响轴温的因素的选择也是研究轴温预测的一大难点。在列车行驶过程中,如能够对轴温进行实时监测预测,进而提前发现潜在轴承故障进行分级预警,为相关人员争取到更多的处理时间,为及时调整行车策略提供更多参考依据[3]。
在轴温预测的研究方面,Sciascera 等[4]简化了热网络模型,因而更加高效准确地对电机绕组的温度进行了预测。赵志刚等[5]采用支持向量机(SVM)的方法对太阳电池温度预测,结果显示具有较高的精度。冯勇等[6]先分析了切削温度的影响因素,进而研究了最小二乘支持向量机(LSSVM)方法的可行性。赵洪山等[7]以风电机轴承为研究对象,先对轴温影响参数进行选择,进而选择最小二乘支持向量机(LS-SVM)来对轴温进行预测,结果显示该方法具有较好的表现效果。Neurouth[8]在构建热网络方法进行温度分析时,通过简化影响微弱的因素,进而在保证模型精度的情况下简化模型。郭鹏等[9]采用NSET 的方法对齿轮箱温度预测,具有较高的精度。李大中等[10]以风力发电为研究对象,选用NSET 方法对发电机后轴承温度作预测,其中模型输入变量参数根据灰色关联度来选取,模型的性能采用预测值与实测值的残差来评价。孟建军等[11]将通过修正灰色二次回归及GM(1,1)模型权重的占比,动态的修正模型,结果显示该方法具有一定的效果。
为了合理有效地选择建模变量,采用灰色关联度分析方法对轴温相关因素进行选择。通过分析幂函数、指数函数及一次多项式为基函数的单一函数的预测结果,在不同的温差条件下,进行分段预测,不同的温差选择不同的基函数进行轴温预测。在低温差阶段采用了基于组合多基函数的预测模型,并通过及时地更新输入数据及根据预测模型上一时段的偏差量,对模型进行加权组合来修订误差,并选用某车履历轴温数据对模型进行验证。
1 数据分析处理
1.1 轴温变化特点
列车轴温随着速度跟列车运行时间而不断变化。基于采集的轴箱轴承温度与对应速度的变化情况如图1 所示,可以发现轴承温升波动情况与温度变化情况可以很好地契合,这也意味着列车运行速度对轴温起着重要的作用。每一次列车的加速伴随着轴温的升高,当列车惰行时,轴温变化趋于缓慢,当列车减速时,轴温将随之下降。可以发现,轴温的急速升高发生在列车牵引启动阶段,当采取制动措施后,轴温趋于近乎单调下降,在另外的区间段内,随着列车运行工况的牵引—惰行—制动的变化,轴温变化趋势具有类似性。此外,由于温度的响应较温度变化慢,温度变化是一个缓变的过程,因而温度变化情况较速度存在滞后现象。
1.2 基于灰关联分析的轴温影响因素
称rij=为Xi与Xj的灰 色相对关联度,也称为相对关联度,关联度分析结果见表1。

表1 关联度分析结果
关联度的取值范围为[0,1],当关联度在0~0.1 范围内时表示为不相关,为0.1~0.3 表示为有微弱关系,0.3~0.5 为相关程度为中等,0.5~1.0表示为相关程度较高。
1.3 数据处理
轴箱轴承温度传感器安装与轴承座盲孔内,受外界干扰及传感器自身的影响,采集的轴温数据不可避免地存在缺失、重复等问题,因而在建立模型前先要对原始采集的数据进行处理,以此保证模型的精度。对轴温数据中明显不符合常识的数据点进行删除,对某一时刻存在缺失的数据进行插值处理,对轴温信号作平滑处理也有利于提高模型的准确度,按式(2)对温度进行平滑处理。
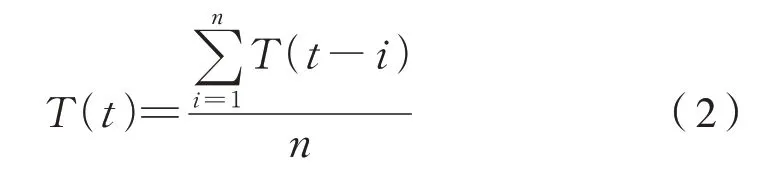
1.4 不同温差条件下的轴温分析
(1)轴承与环境温差较低
当T-Ta≤r=10 时,其中T为 轴承 温 度,Ta为环境温度,表示为轴承温度与环境温度的温差较低。这种情况一般为车辆在长时间的停车后,轴温与环温很接近。当再次启动的时候,车辆工况由静止到牵引加速启动,轴承转速加快,进而由于轴承内部摩擦快速产生热量。由于轴温与环境温度差别较大,轴温升高速度较快,故而采用变化速度较快的指数函数作为该阶段的基函数进行轴温预测。
(2)轴承与环境温差较高
当T-Ta>r时,即轴承温度与环境温差较高时,在此时车辆由于持续的加速或匀速运行,轴温与环温温差较大,但此时由于轴温接近临界值,因而不会持续增大,故温度变化相对低温差阶段较为缓慢。在用一次线性多项式预测轴温时,预测值较实际值偏大,幂函数预测值比实际值偏小,因此对这2 个基函数进行加权组合,进而得到最终的预测结果。
为了保证模型的预测精度,在不同的温差条件下分别选用不同的基函数对轴温进行拟合预测。 组合最小二乘回归预测模型流程如图2所示。
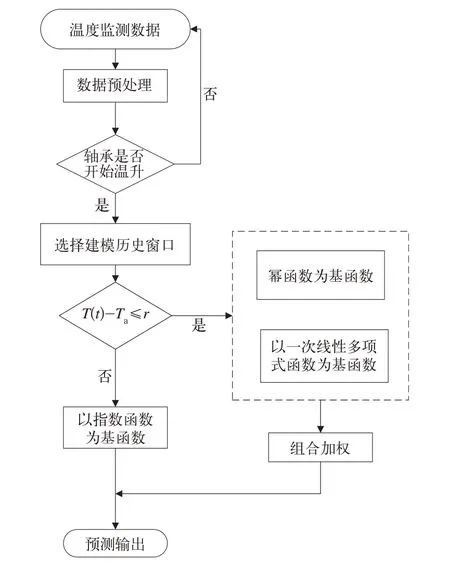
图2 组合最小二乘回归预测模型流程
根据环境温度与轴温的差值,轴温的预测分为高、低温差2 种情况,并根据这2 种情况下轴温变化速度的快慢选择不同的基函数对其进行预测。当T-Ta≤r时,由于轴温变化较快,因而选择能跟踪变化较快轴温的指数函数作为基函数对轴温进行跟踪预测,当轴温与环温的温差大于设定阈值时,以一次线性多项式与幂函数为基函数,对其进行加权组合来预测轴温。
2 基于多基函数组合的高速列车轴温预测模型
高速列车在某一线路运行时,将多个区间段内的多个站点紧密连接起来,由于区间段内站点较多,因此车辆需要频繁的启停操作,每次的启停过程中,轴温的变化具有相似性,启动时轴温升高较快,惰行时轴温变化缓慢。通过分析历史履历数据中轴温与对应速度之间的变化情况,得出轴温会随着列车运行的速度变化而变化。为简化模型,选择某一区间段内列车从启动加速到减速制动前,这一近似单调不减阶段的轴温进行预测分析,选择的轴温履历数据为邻近时间点的数据。
2.1 最小二乘回归法原理
建模前因变量y与自变量x之间的映射关系y=f(x)是未知的,需根据已知样本{xi,yi}i=1,2,3,…,n来反推,其中xi=(x1,x2),x1表示时间t,x2表示速度v[12],用多项式(3)来对数据进行拟合:
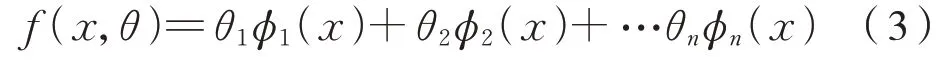
式中:θ1,θ2,…θm是模型待求的m个参数,φ(x)为基函数。模型还可以表示为式(4)~式(6):
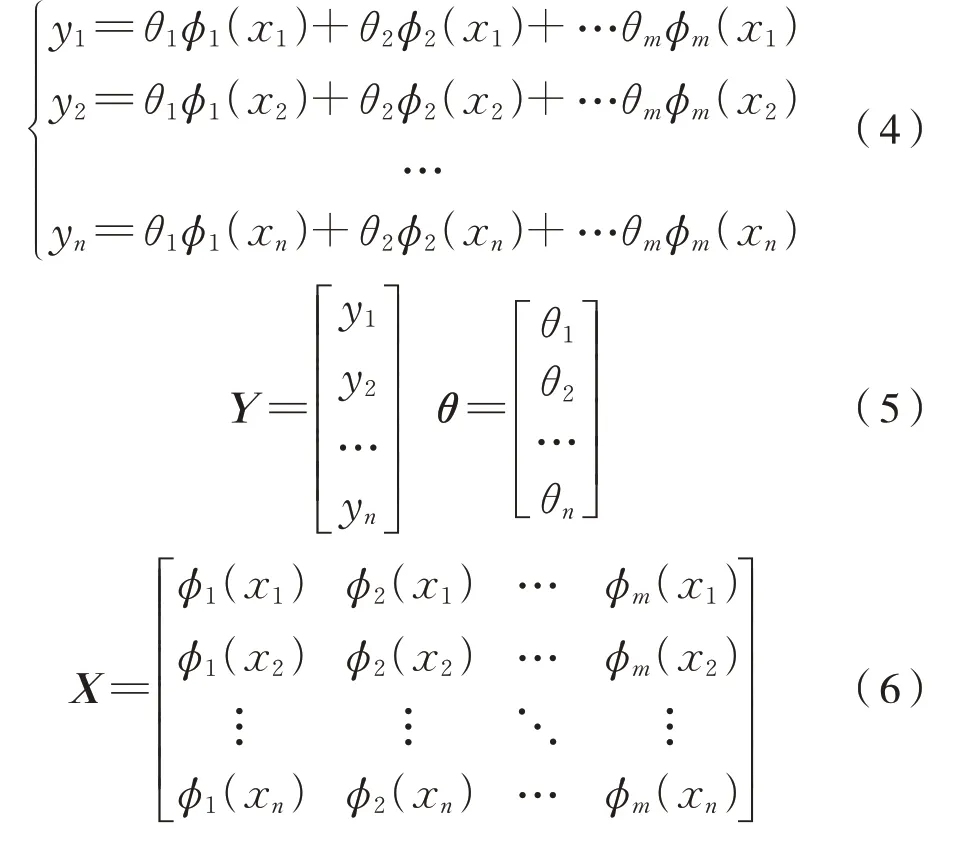
模型可以表示为Y=Xθ的形式,拟合值与原始值差值的平方和为损失函数,为式(7):
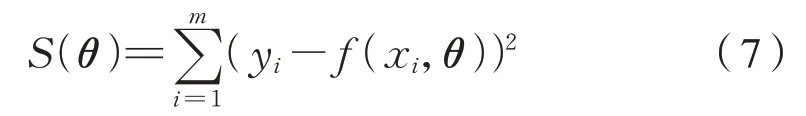
对损失函数求极值以对参数估计为式(8):
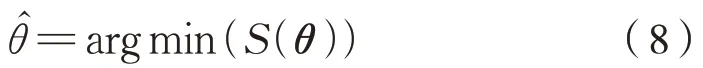
对S(θ)进行求导数,根据来求得 最优参数,估计参数表达式为式(9):
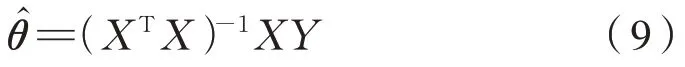
通过代入式(4)可以求得自变量x与因变量y的函数关系。
2.2 不同基函数权重的计算
为增强模型的可比性,选择历史数据中时间邻近的数据,对轴温进行短时预测。在采集的数据中,从轴温开始上升的数据为起点截取数据,直到满足建模所需要的数据点数。根据模型输入数据来拟合数据间的关系,之后对未来n分钟的轴温进行预测。为保证模型能够感应到轴温最新的变化趋势,每预测完n分钟的数据,就将其更新到建模数据中去,来对下一时段的数据进行继续预测。当进行第i次预测时,前一次预测的实测值为已知,可以根据实测值与预测值的偏差来对模型进行动态修正。根据第(i-1)时一次线性多项式φline(x)=ax1+bx2+c与幂函数预测模型φpow(x)=与真实值的误差确定权值w1,w2,以此来修订误差。在(t-n)时一次线性函数与幂函数预测后n分钟输出轴温和实测轴温为式(10):
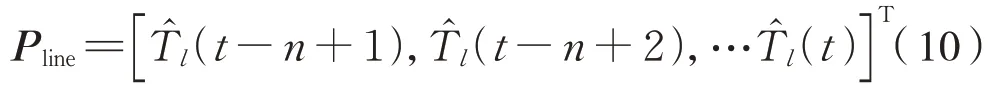
式中:Pline为一次线性多项式预测的轴温值组成的向量。
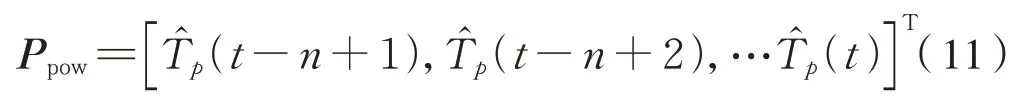
式中:Ppow为幂函数预测的轴温组成向量。
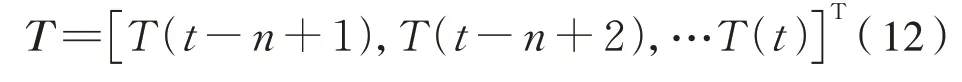
式中:T为基于实测温度值构建的向量。
2 种函数预测值与真实值之间的距离d为式(13):

权重的分配依赖选择的2 个基函数预测值与实际值之间的距离。当实测值与预测值之间的偏差愈小意味该基函数拟合度较好,因而权重占比就越大,反之亦然。

式中:wline为一次线性多项式函数所占权重;dpow为幂函数预测向量与实测向量之间的距离;∑d为2种基函数预测向量与实际向量距离之和。

式中:wpow为以幂函数为基函数时的占比;dline为用一次线性多项式为基函数时的轴温预测值与实际值残值的绝对值;∑d为2 种基函数预测输出向量与实际输出向量距离之和。
在t时刻将n个轴温监测数据进行更新,不断纳入最新的轴温数据到建模窗口中,并根据最新的输入轴温向量对下一时段轴温进行预测,根据t-n时刻轴温的预测偏差来加权修正模型。得到重构模型为式(16):
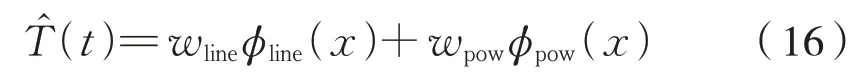
式中:wline为一次线性多项式为基函数时的占比;wpow为以幂函数为基函数时的占比;T^ (t)为温度预测值;φline(x)为以一次线性多项式为基函数时的轴温预测值;φpow(x)为选用幂函数为基函数时的轴温预测值。
2.3 多基函数组合预测模型
根据车辆运行状态的不同,轴温与环温的差值随之不同,因而将车辆运行划分为高、低温差2种情况,根据这2 种情况下轴温的增长速率不同,选择不同的基函数来对轴温进行拟合预测,在t时刻的组合预测模型表达式为式(17):
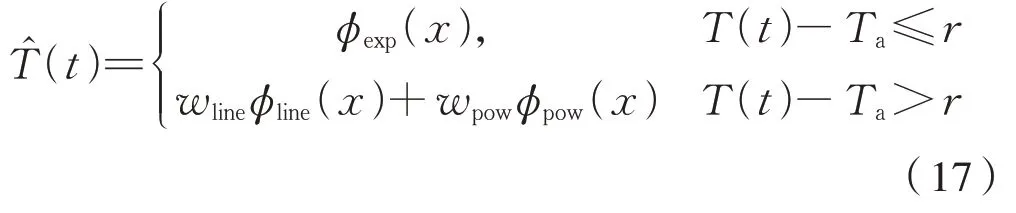
T(t)-Ta≤r时 ,以 指 数 函 数φexp(x)=aexp(bx1)+cexp(dx2)为基函数建立最小二乘回归模型;T(t)-Ta>r时,采用多基函数加权组合的预测模型。
2.4 预测误差评价指标
为对模型进行较为全面的评价,选择局部与整体误差刻画指标对模型进行分析。模型评价指标见表2,表2 中T^i表示轴温的预测值,T表示轴温的实测值。
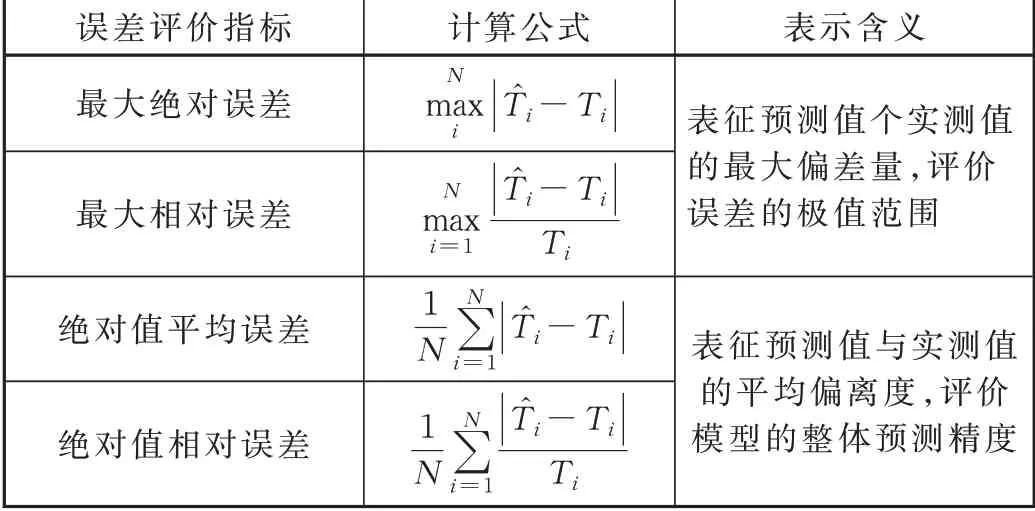
表2 预测误差评价指标
3 基于多基函数最小二乘回归法的高速列车轴温预测
以某型高速列车履历服役轴温监测数据为例,来验证文中提出的模型的准确性与可靠性。其中车载轴温监测系统所用的温度传感器为pt100,采样频率为1/60 Hz,轴温数据每分钟采集1次,列车温度传感器安装如图3 所示。根据轴箱轴承采集的温度数据来对模型进行分析,截取列车在某个区间段内轴温开始上升到车辆制动前这一近似单调不减阶段的数据,根据轴温与环温的差值,采用多基函数组合的最小二乘预测模型对轴温进行拟合预测,通过不断更新输入数据以及动态修正权值,对模型进行修正,以此提高模型的精度。

图3 列车温度传感器安装示意图
以某车履历轴箱温度数据为例,其原始数据、基于多基函数组合模型的预测值及基于单一函数的预测曲线如图4 所示,预测误差结果见表3。
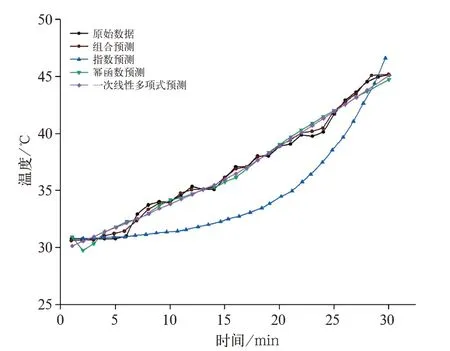
图4 轴箱温度预测曲线
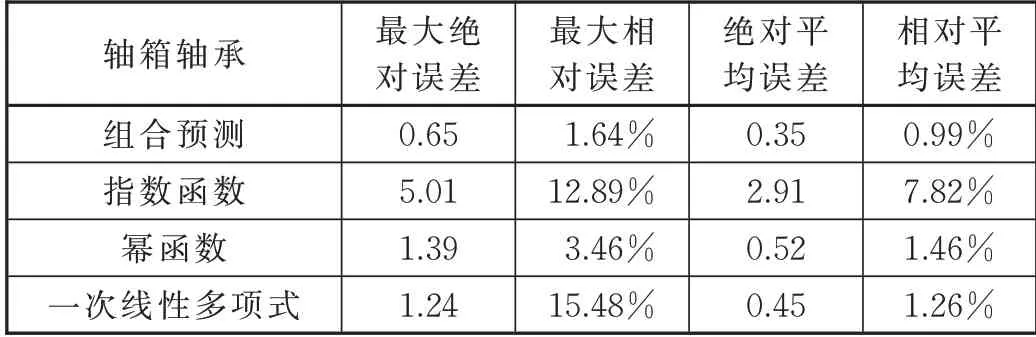
表3 轴箱轴承温度预测误差
以评价模型误差的指标对模型进行分析,通过对比组合预测与3 种单一预测函数的结果发现,组合预测的最大绝对误差为0.65,较指数函数降低了87.0%,较幂函数降低了53.2%,较以一次线性多项式降低了47.6%。最大相对误差为1.64%,绝对平均误差为0.35,相对平均误差为0.99%,较其他单一函数的预测评价指标也得到了较大的提高,预测结果也更加接近真实值。
4 结 论
(1)以轴箱轴承为例,用灰色度关联的方法对轴温相关因素进行选择,采用基于多基函数组合的最小二乘回归法进行轴温预测。通过对预测结果对比分析可知,组合预测模型误差较其他单一函数的模型明显变小。表明组合预测精度要优于3 种采用单一基函数的最小二乘回归预测精度。
(2)基于列车履历服役轴温监测数据,分别采用不同基函数的最小二乘回归预测法对轴温进行预测。分析不同基函数的预测误差,并根据轴温与环温的温差分为高温差与低温差2 个阶段,在不同的温差阶段选用不同的基函数进行预测,根据前一阶段的预测偏差对模型采用加权组合的方法进行校正,并基于某车实际服役轴温数据进行模型的验证,通过对异常轴承温升点作短时预测来提前实现温度预警,提前发现潜在的轴承故障,为处理异常轴温争取更多的处理时间,为行车策略调整提供依据。
