城市轨道交通站台客流聚集模型研究
2022-07-15肖飒蒲琪
肖 飒 蒲 琪
(同济大学铁道与城市轨道交通研究院, 201804, 上海∥第一作者,硕士研究生)
城市轨道交通换乘车站相较于非换乘车站更易形成大客流聚集,准确计算换乘车站站台最高聚集人数可为站台客流压力评估提供重要的基础数据。目前,对于换乘车站站台聚集人数的研究还处于初级阶段。文献[1]在文献[2]的基础上,将换乘客流视为周期性进入站台,在两线列车到达间隔时间相同且恒定的条件下,得到了单侧线路客流在站台的最高聚集人数的方法。大多数学者建立换乘站站台聚集人数模型的技术路线为:将站台客流分为上车客流和下车客流,假定进入站台的上车客流为均匀分布、列车到达时间间隔恒定、不考虑滞留乘客,在这些前提条件下获得站台最高聚集人数。但大部分模型中并未考虑滞留乘客的影响,换乘线路发车间隔对聚集人数模型的影响亦还未考虑。
1 换乘车站站台聚集人数模型研究条件设定
1.1 客流分析
将客流划分为上车客流和下车客流;将进站客流划分为进站上车客流、换乘上车客流和滞留客流;将下车客流划分为换乘客流和出站客流,两者可合并为下车客流一并研究。本文将乘客进站、出站、上车、下车的速率视为匀速[3-4]。
早高峰时期,客流量较大,当上车客流量大于列车剩余输送能力时,站台出现乘客滞留。第k趟列车离开站台时的滞留乘客为:
Ra,k=max(Nall+Ra,k-1-Sa,k,0)
(1)
式中:
Ra,k——1个列车行车间隔内,第k趟列车离开站台a时的滞留乘客数量,其中Ra,0=0,人;
Nall——1个列车行车间隔内,a站台等待上车乘客数量,人;
Sa,k——1个列车行车间隔内,a站台登上列车乘客数量,人。
Ra,k有两部分来源:上一轮的滞留人数Ra,k-1,本次列车的未上车人数Nall-Sa,k。其中,Nall包含换乘上车客流和进站客流两部分。
1.2 乘客上下车方式确定
根据乘客上下车行为不同,本文讨论如下两种极端的上下车方式:
1)方式1:乘客不遵守先下后上的原则,车上乘客的下车过程和站台乘客的上车过程同时发生,一直处于混行状态,此时上下车时间均等于列车的停站时间。
2)方式2:乘客严格遵守先下后上原则,当下车乘客下车完成之后,站台乘客才开始上车,此时上车时间与下车时间之和为列车的停站时间。
由以上分析可知,乘客上下车过程实际上应当是这两种方式共同发生的情况。
1.2.1 非换乘乘客侧式站台上下车混行模式
这种情况下,乘客在站台上的聚集状态呈现出显著的周期性,以列车的行车间隔为周期动态变化。此时在1个周期内标记关键时刻,如图1所示。

注:x1,k为第k趟列车到站时刻;x2,k为第k趟列车关门离站时刻;x3,k为第k趟列车的下车乘客疏散完毕时刻(高峰时期,设x3,k>x2,k);x1,k+1为第k+1趟列车到站时刻。
由图1可知,列车行车间隔ta=x1,k+1-x1,k。以前一列列车关闭车门离站时刻x2,k作为研究起始点,站台聚集人数可以划分为3个阶段:①x2,k—x3,k阶段:存在进站乘客进站和下车乘客离开站台两种情况;②x3,k—x1,k+1阶段:只存在进站乘客进站。③x1,k+1—x2,k+1阶段:存在进站乘客上车和到站乘客下车两种情况。这3个阶段中,站台聚集人数的变化趋势如图2~5所示。
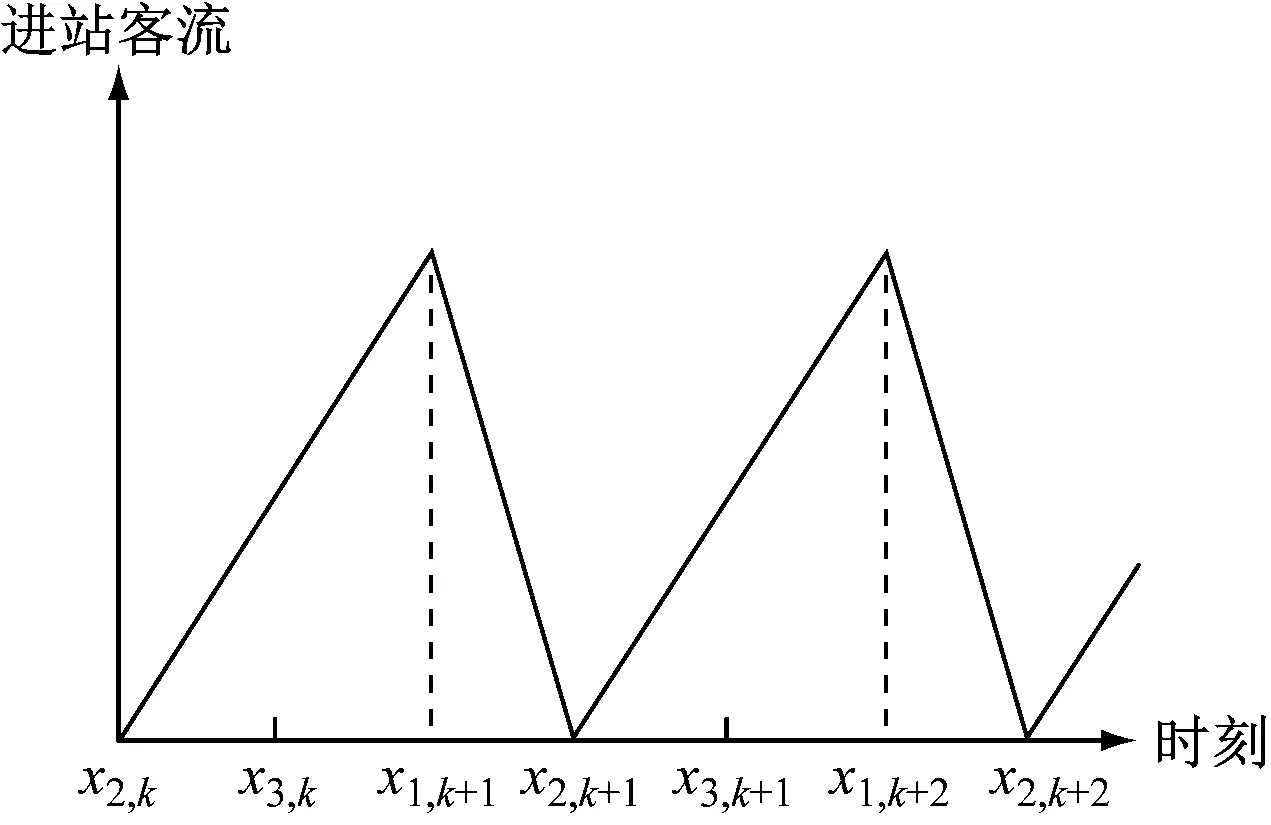
图2 站台进站客流变化曲线Fig.2 Variation pattern of inbound passenger flow on platform
1)x2,k—x3,k阶段站台聚集人数q1(x):此时站台同时存在下车乘客疏散和上车乘客进站两个过程。因此,该阶段站台聚集人数可以表示为:

图3 站台下车客流变化曲线Fig.3 Variation pattern of alighting passenger flow on platform

图4 混行模式客流变化曲线Fig.4 Variation pattern of passenger flow in mixed mode

图5 混行模式客流变化曲线Fig.5 Variation pattern of passenger flow in mixed mode
q1(x)=v0(x3,k-x2,k)+(vm-v0)(x-x2,k)
(2)
式中:
v0——下车乘客离开站台的平均速率,人/s;
vm——进站乘客到达站台的平均速率,人/s。
2)x3,k—x1,k+1阶段站台聚集人数q2(x):在此阶段,前一列列车的乘客已疏散完毕,只存在进站上车乘客。因此,该阶段站台聚集人数可以表示为:
q2(x)=vm(x-x3,k)+q(x3,k)
(3)
式中:
q(x3,k)——x3,k时刻站台聚集人数。
将q(x3,k)代入式(3),可得:
q2(x)=vm(x-x2,k)
(4)
3)x1,k+1—x2,k+1阶段站台聚集人数q3(x):此阶段为车门开启时间段,在此阶段同时存在乘客的上车行为和下车行为。因此,该阶段的站台聚集人数可以表示为:
通过参加职业技能大赛,贵州电子信息职业技术学院大大提升了在贵州省甚至全国的专业知名度,贵州移动、联通、电信等公司主动与贵州电子信息职业技术学院建立校企合作关系。通过校企合作,学生的毕业论文、职前训练、顶岗实习都在与专业相关企业进行。学校原先的毕业设计模式为教师根据所学内容划范围、学生选题;进行校企合作后改革为根据实际岗位群的生产案例提供选题范围、校企双方共同把关、学生最后确定课题的新模式。这种模式提高了学校学生的实用岗位能力[4]。
q3(x)=(vm+vc-v0-va)(x-x1,k+1)+
vm(x1,k+1-x2,k)
(5)
式中:
va——乘客上车平均速率,人/s;
vc——下车乘客平均速率,人/s。
由式(2)—式(5)可得,在1个列车行车间隔ta内,混行模式下的聚集人数变化均符合线性变化规律。为方便起见,分别用r1、r2、r3表示3个阶段的站台聚集人数变换率,即:
(6)
进站乘客一般具有随机特性,从不同位置随机到达车站,呈现出比较平稳的特性。下车乘客由列车运送到达,因此呈现出周期性的特点。v0一般受限于楼扶梯的通行能力,因此v0较为接近楼扶梯的最大通行能力。统计数据显示,vm通常小于最大通行能力。一般情况下,vm
根据上述分析可得,在非换乘乘客侧式站台上下车混行模式下,侧式站台最大聚集人数Q1(x)为:
Q1(x)=max{q(x1,k),q(x2,k)}=
(7)
在前一种模式的基础上,添加一个下车乘客全部完成下车、上车乘客开始上车的时刻xt,k时刻,如图6所示。

图6 非换乘乘客侧式站台先下后上模式示意图
同理,在先下后上模式下,任意时刻的站台聚集人数q(x)可以表示为:

(8)
同理,在非换乘乘客侧式站台先下后上模式下,侧式站台最大聚集人数Q2(x)为:
Q2(x)=q(xt,k+1)=vm(xt,k+1-x2,k)+
(vc-v0)(xt,k+1-x1,k+1)
(9)
当混行模式下的r3>0时,Q1(x)=v0(x3,k-x2,k) 根据换乘客流到达车站的时刻与列车的停站时刻的不同关系,可以分为3类,如图7所示。为获得最大聚集人数模型,因选择图中③时刻作为换乘乘客到站时刻,如图8所示。 注:xh,k为换乘客流到站时刻;xt,k为下车完成时刻。图7 客流到达示意图Fig.7 Schematic diagram of passenger flow arrival 注:xc,k为B线路换乘客流全部到站时刻。图8 A线路下车结束后B线路换乘客流到达站台 按照前述的阶段划分方式,在A线路的1个列车行车间隔ta内,同样以前一列列车关闭车门离站时刻x2,k作为研究起始点,换乘客流站台聚集人数可以划分为4个阶段:①x2,k—xh,k阶段:此阶段无换乘客流到达站台;②xh,k—xc,k阶段:换乘客流陆续到达站台,聚集在A站台上;③xc,k—xt,k+1阶段:换乘客流聚集在A站台上;④xt,k+1—x2,k+1阶段:换乘客流和进站客流一起完成上车过程。其变化规律如图9所示。 注:Nb为换乘总人数。图9 站台换乘客流变化曲线Fig.9 Variation pattern of transferring passenger flow on platform 将上车客流与下车客流按照时间同步叠加可得单侧车站的换乘客流聚集人数qa(x),可以表示为: (10) 在列车运行过程中,滞留人数Ra,k会以列车行车间隔ta为周期,周期性出现和消失。根据式(1)可得滞留人数的判断公式为: Ra,k=max(Nb+vmta+Ra,k-1-va(x2,k-xt,k),0) (11) 在1个列车行车间隔内,滞留人数的变换只存在于上车阶段,其余时间段均保持不变。因此,滞留人数的变换只需要考虑[xt,k+1,x2,k+1]时间段。由于此阶段持续时间较短,可将变换视作从Ra,k到Ra,k+1的匀速率变化过程。滞留人数聚集模型Ra,k(x)为: (12) 综上所述,侧式换乘站台聚集人数qtran(x)可以通过先下后上的侧式非换乘车站聚集人数、换乘客流聚集人数、滞留人数通过时间同步叠加获得,即: qtran(x)=q(x)+qa(x)+Ra,k(x) (13) 由此可得侧式换乘车站聚集人数模型: (14) 根据前述分析可得,岛式换乘车站聚集人数模型q岛(x)可以通过上行侧式换乘车站聚集人数qtran,+(x)和下行侧式换乘车站聚集人数qtran,-(x)经同步叠加获得: q岛(x)=qtran,+(x)+qtran,-(x) (15) 在计算最大聚集人数时,由以上分析可知,当上行和下行列车同时完成乘客下车过程时,在xt,k这一时刻的聚集人数将达到最大值。因此,岛式换乘车站最大聚集人数Q3(x)为:Q3(x)=qtran,+(x)(xt,k)+qtran,-(xt,k)。 为了验证本次研究模型的适用性、有效性,以上海轨道交通11号线(以下简为“11号线”)江苏路站的岛式站台作为研究对象,获得模型所需的相关参数;利用岛式换乘车站聚集人数模型,得到最高聚集人数发生时刻;使用Anylogic仿真软件构建仿真模型,得到站台聚集人数分布规律;比较公式计算和仿真软件的结果,进行误差分析。 11号线江苏路换乘车站为典型非同台岛式换乘车站,其客流特征、客流来源、换乘方式等满足研究要求,可以作为验证聚集人数模型的实例站台。选择换乘客流最大的工作日08:30—09:00时间段作为研究时间。根据列车运行时刻表及车站视频数据资料可以得到如下参数:①vm=0.45人/s(根据视频数据观测可得,上行方向上车的客流约占65%,下行方向上车的客流约占35%,可近似认为上行方向进站客流速率为0.3人/s,下行方向进站客流速率为0.15人/s);②va=1.8人/s;③ 换乘上车客流平均速率6人/s;④vc=1.36人/s;⑤v0=8人/s。 根据视频数据统计得到,在早高峰期间,列车运能可以满足乘客需求,因此11号线江苏路站的上车客流不存在未上车的滞留乘客,即:Ra,k=0。 按照岛式换乘站台聚集人数模型,可得岛式换乘车站聚集人数模型,如图10所示。 图10 模型计算的11号线江苏路站站台聚集人数分布图 由图10可见,站台最大聚集人数出现在上下行列车同时完成下车过程的80 s时,达到了1 252人,即上行侧最大聚集人数644人和下行侧最大聚集人数608人。同时可以看到,在230 s时的聚集人数相邻峰值的数值差异主要是由上下车到达时刻不同所致,200 s时的聚集人数峰值是由上行侧列车到站客流产生的。 采用Anylogic仿真软件搭建模型,按比例建立的11号线江苏路站站台模型如图11所示,站台相应的设施按照比例尺等比例放置。通过行人库建立逻辑关系,即包括进站客流、换乘客流和出站客流的控制模块。 图11 11号线江苏路站站台仿真模型图Fig.11 Simulation diagram of platform simulation model of Shanghai Rail Transit Line 11 Jiangsu Road Station 聚集人数的采样时间频率设置为1 s,每隔1 s采集1个聚集人数样本,共采集600个数据,通过Anylogic仿真软件的数据输出功能统计最大聚集人数,如图12示。图12采用模型运行稳定后20~30 min时间段的数据。 由仿真结果可知:本次仿真站台的最高聚集人数为1 237人,出现在26 min时,即上下行列车同时到达站台的时刻;站台的聚集人数根据时间变化而变化,每当上下行列车同时到达站台并且换乘乘客全部到达站台时,可以达到最高聚集人数1 237人,相对误差-1.24%;聚集人数呈现出以10 min为周期的变化规律。 图12 仿真计算的11号线江苏路站站台聚集人数分布图 为了验证本文提出模型的有效性,得到10组站台最大聚集人数仿真计算结果与模型计算结果的相对误差,如表1所示。由表1可见,站台平均聚集人数为1 258人,平均相对误差为0.47%;10组仿真结果的相对误差均在3%之内。由此可见,模型计算的站台最高聚集人数可以有效反映仿真计算的站台最高聚集人数。 表1 站台最大聚集人数仿真计算与模型计算的相对误差 以列车行车间隔为研究周期,分析乘客在站台的集散过程,建立了换乘车站站台最大聚集人数计算模型。将站台客流分为进站客流、换乘客流和出站客流,获得了基于列车时刻表的换乘站台聚集人数模型,并且通过Anylogic仿真软件验证了站台聚集人数模型的有效性和适用性,可为城市轨道交通换乘车站站台客流压力评估提供理论支撑。 本次研究所建立的站台聚集人数模型中,客流的到达采用的都是匀速到达模式。而在实际中,会存在个体的差异性,将该差异对模型精准度的影响作为下一步的研究方向。2 岛式换乘车站站台聚集人数模型



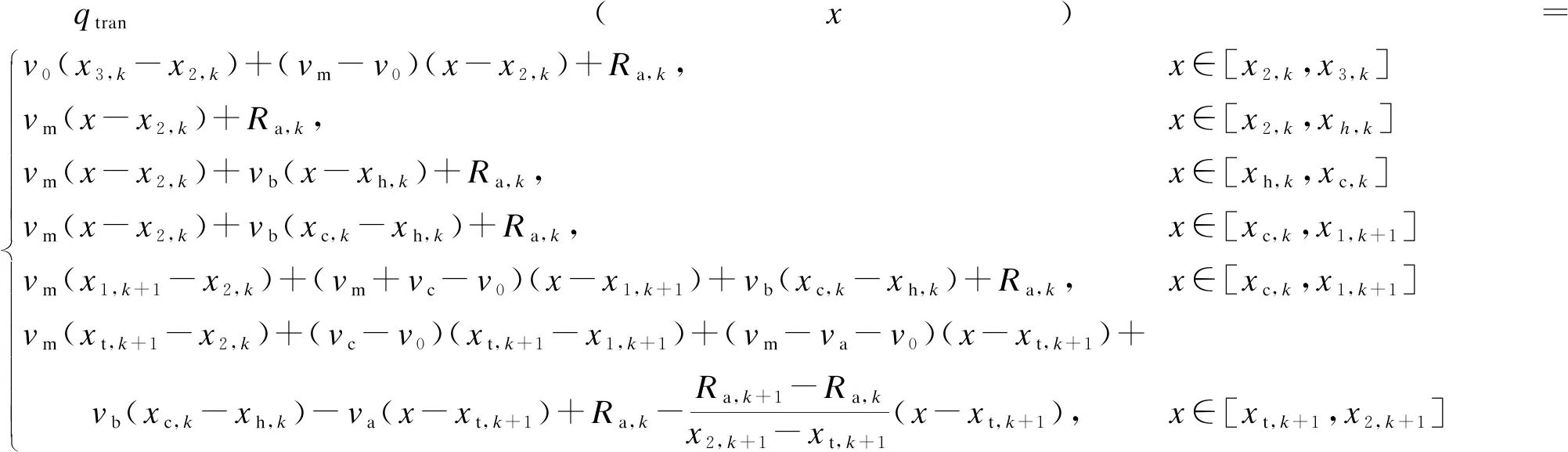
3 案例模型计算与仿真验证
3.1 计算参数
3.2 模型计算结果分析

3.3 仿真验证



4 结语
