基于D-S证据理论的城市轨道交通车辆车门亚健康融合诊断方法

史华东 陆宁云 许志兴 陈健飞

(1.南京航空航天大学自动化学院， 211106， 南京；2.南京康尼机电股份有限公司， 211106， 南京∥第一作者， 硕士研究生)

通过对城市轨道交通车辆车门系统健康状态的监测发现，随着列车的持续运行，车门各部件由于元件老化及磨损会导致车门处于亚健康状态，直接影响着车门的正常使用性能[1]。及时发现并准确诊断城市轨道交通车辆车门的亚健康状态对其安全运行与高效率的维护具有重要意义。

文献[2]提出一种基于信息增益率的随机森林方法，构建了车门故障诊断模型。文献[3]通过特征优选算法筛选出最优特征子集，利用随机森林算法实现了地铁车门微小故障诊断。文献[4]基于JS散度，计算车门实时状态与参考健康状态的数据统计分布相似性，以检测车门系统的异常状态。上述故障诊断方法均基于单一数据源进行研究，采集的车门信息不够充分，导致最终诊断结果的准确性和可靠性较低。为此，本文提出基于D-S证据理论的车门亚健康融合诊断方法。对车门驱动电机数据与电子控制器I/O(输入/输出)信号，分别利用K-means聚类与贝叶斯推理得到亚健康初步诊断结果，再基于D-S证据理论在决策层进行信息融合，构建更加精确的车门亚健康诊断模型。应用结果表明，该方法可显著提高车门亚健康诊断模型的可靠性和准确性。

1 城市轨道交通车辆车门控制系统

1.1 车门结构及其亚健康类型

本文以南京康尼公司的电动双开塞拉门作为研究对象。其车门主要由承载导向机构、门控系统、传动锁闭机构、密封装置等部分组成。除了基本的机械结构，车门核心的门控系统主要由电子门控器与行程开关等电气部件构成。门控器作为控制中心，负责发出开关门指令信号，同时能够接收行程开关反馈的开关量信号。

在列车长期的运营中，环境多变、乘客挤压及车门维保不及时等原因使车门部件易出现松动、失效、间隙等情况，进而导致车门处于亚健康状态运行。这些微小的亚健康状态往往具有隐蔽性、偶发性与模糊性，难以被及时发现。根据地铁车门健康状态监测的实际需求，本文研究了表1中所列的7种亚健康类型。

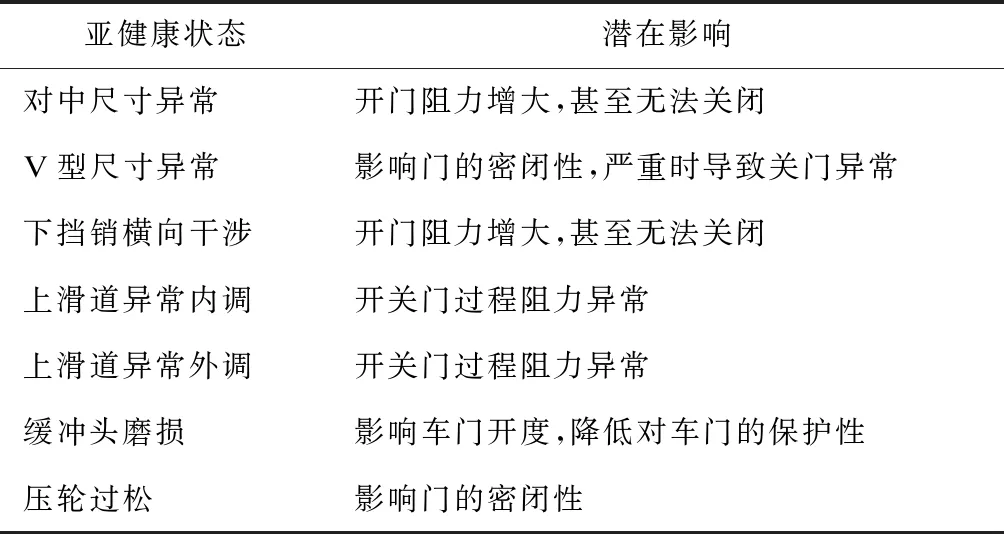
表1 车门亚健康状态

1.2 车门可测量数据

基于数据驱动的故障诊断方法对离线数据的信息充足性和完整性有一定的要求[5]。通过轨道交通车辆车门远程监控与故障诊断系统[6]在车门上的应用，实时获取车门运行数据。这些数据包含了详细的车门状态信息，可充分满足基于数据驱动的故障诊断要求。

地铁车辆车门通过传感器采集的数据主要分为驱动电机数据和智能门控器I/O信号两类。这两种不同类型的数据所反映的车门信息具有较大的差异性，驱动电机数据主要反映车门连续运动过程中的特点，门控器I/O信号包含了车门受控系统信息，可以反映车门状态的时变特性。

本文采集的电机数据包含转速、转角、电流3个变量。图1为正常开关门过程中车门电机数据曲线图。由图1可知，正常1次开关门的时间约为3.5 s。传感器采样周期为10 ms，每条数据大约采样350个点。

门控器I/O信号共包含了车门系统20种不同的控制信号与开关反馈信号。这些信号量为典型的离散数据信号，其状态只用数字0和1表示。表2为具体的I/O信号量类型。在车门开关门过程中，与车门状态变化相关的信号量较少，因此I/O信号较之电机数据包含的车门信息相对缺乏。

图1 正常开关门过程车门电机数据曲线Fig.1 Vehicle door motor data curve of normal opening- closing process

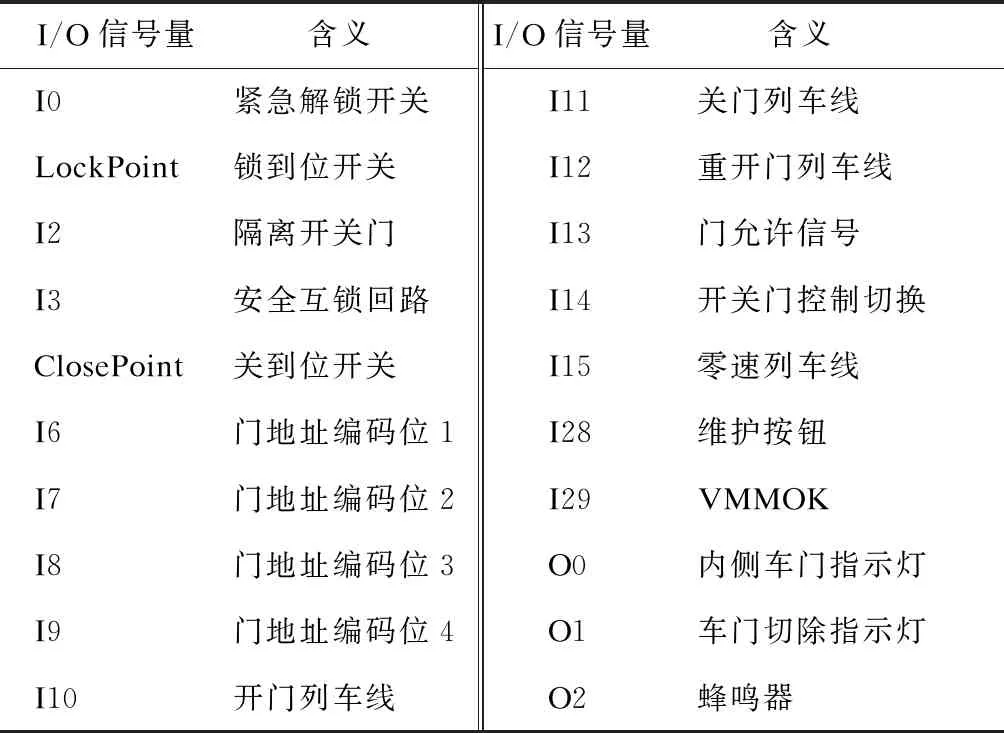
表2 门控器I/O信号量

2 基于D-S证据理论的车门亚健康融合诊断方法

2.1 D-S证据理论

D-S证据理论作为一种常用的信息融合方法，其提供的理论方法可以进行证据间的合成，在不确定性的表示和组合方面具有较多优势。在D-S证据理论中，假设研究对象的所有相互独立、互斥的事件结果用集合Θ表示，集合Θ称为识别框架。对识别框架中的某个事件∀A⊆2Θ，映射m：2Θ→[0,1]需满足：

(1)

式中：

∅——空集；

m——基本概率分配(BPA)函数；

A——研究对象发生的可能事件。

m(A)为事件A发生的基本概率分配值，表示对结果A的信任程度。此外，定义信任函数Bel(A)与似然函数Pl(A)来表示多子集事件A发生的所有可能概率。

(2)

(3)

式中：

B——事件A的子集事件。

Bel(A)表示对事件A发生的支持程度，Pl(A)表示对事件A的不怀疑程度，两者共同构成事件A的信度区间[Bel(A)，Pl(A)]。

当同一个识别框架下出现多个证据体能够对被测对象的结果进行独立判断时，可以通过D-S证据合成规则进行组合，得到新的基本概率分配结果m12。假设m1和m2为两个独立事件B、C的基本概率分配，进行组合后的结果为：

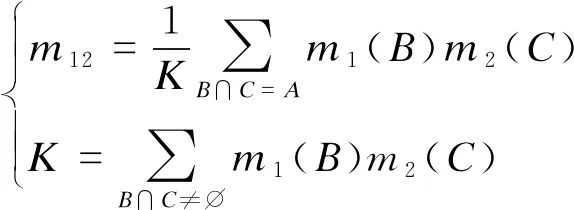
(4)

式中：

K——冲突系数，表示证据之间的冲突程度。

2.2 车门数据预处理

车门部件发生损坏、尺寸变化、处于亚健康状态等情况时，都会导致电机的输出曲线发生变化。为了准确区分每种亚健康状态，根据车门的运动特点，将车门整体运动过程分为升速段、高速段、减速段、缓行段与到位后段，具体分段如图2所示。

根据图2车门运动过程的阶段划分，对电机的3个测量数据进行时域特征提取。本文提取的特征包括最大值、最小值、均值、峰值、方差、偏度、峭度，以及每段车门数据的行程与时间。对每个电机参量提取93个特征值，在每条数据中共提取279个特征组成特征向量F=[F1,…,F279]。

图2 车门运动过程阶段划分Fig.2 Door movement stage division

针对门控器I/O信号的特点，采用基于多信号模型故障测试性分析的思想进行分析，通过测试生成车门亚健康依赖矩阵D。对车门I/O信号数据进行离散化处理，提取1次开关门过程中所有I/O信号的跳变状态与跳变时间，组成的序对信息形式如下：

Zj={(0,tj,1),(0,tj,2),(0,tj,3),…,(0,tj,k)}

(5)

式中：

Zj——门控器I/O信号参数；

j——变量索引；

tj,k——Zj的状态跳变时间；

k——Zj的所有状态跳变次数。

将所有I/O变量跳变时刻tj,k选作测试点，生成测试区间[tj,k-Δ,tj,k+Δ](Δ为测试区间的时间间隔)。在每个测试区间内，对亚健康数据集进行测试，I/O变量若发生正确的跳变，则将D中对应元素赋值为0，否则赋值为1。通过测试得到开门与关门两个亚健康依赖矩阵，建立起车门I/O信号的触发时间、触发状态与车门亚健康状态之间的联系。

2.3 基本概率分配函数的构造

针对车门的电机数据与I/O信号，本文采用了不同的亚健康初步诊断方法，且其各自的决策层基本概率分配构造方法也不同。

电机数据基于K-means聚类相似度构造BPA。对预处理后的车门电机数据特征值进行编号，应用K-means聚类算法进行分析，当聚类成功时将得到正常与亚健康两个聚类中心。根据两个聚类中心之间的特征值距离大小对特征进行排序，该特征值距离大的代表该特征在分类中作用明显，取排序前20个特征作为区分特征。为了对聚类结果进行识别，根据两类数据的特征大小对特征的编号标注“正负号”(亚健康数据的特征相对正常数据变大时为“正号”，否则为“负号”)。通过计算测试数据区分特征与已知亚健康模型区分特征之间的相似度进行亚健康的模式识别与诊断。因此，基于K-means聚类结果构造BPA的计算式为：

(6)

式中：

Ai——车门可能发生的亚健康类型；

F(Ai)——测试数据的亚健康聚类结果与亚健康特征模型的相似度。

I/O信号基于朴素贝叶斯分类构造BPA。可将发生跳变的I/O信号量作为样本的属性，亚健康将矩阵中每个测试点的赋值结果作为样本对应属性的取值。基于属性条件独立性假设，贝叶斯推理的输出为每种亚健康发生的后验概率，而贝叶斯推理的先验概率可以通过训练数据的亚健康测试矩阵估计得到。假设每个I/O信号数据集中有n个开门数据、m个关门数据，对其进行贝叶斯分类后，将得到n个开门数据的亚健康推理结果与m个关门数据的推理结果，每个推理结果为11种亚健康发生的后验概率。本文将同一个数据集的开门与关门亚健康推理结果各自取平均值，最终每个数据集得到1个开门数据贝叶斯推理结果与1个关门数据贝叶斯推理结果。根据贝叶斯推理结果，构造BPA的计算方法[7]如下：

(7)

式中：

P(cj)——在已知属性为x1,x2,…,xn的情况下，将其分类为cj的概率。

2.4 车门亚健康融合诊断模型

基于D-S证据理论的车门亚健康诊断模型主要由2部分组成：① 第1部分是模型初步诊断层[8]，该层将预处理后的车门数据分别利用K-means聚类与贝叶斯推理得到初步的诊断结果，每种诊断结果将作为下一步决策层融合的证据；② 第2部分为模型的融合诊断层，根据电机数据与I/O信号的初步诊断结果构造各自的基本概率分配m1、m2，应用D-S合成规则将其进行决策层融合得到新的基本概率分配，依据决策规则确定车门亚健康状态。基于D-S证据理论的车门亚健康诊断模型如图3所示。

图3 基于D-S证据理的车门亚健康诊断模型Fig.3 Vehicle door sub-health diagnosis model based on D-S evidence theory

车门亚健康诊断模型的具体实施步骤为：

1) 确定识别框架。根据城市轨道交通车门系统发生的亚健康类型，采集11种车门亚健康状态的车门数据，建立识别框架Θ。

2) 数据预处理。按第2.2节的数据预处理方法对电机数据进行特征提取与标准化、离散性分析；对I/O数据进行结构化处理与测试分析生成亚健康依赖矩阵，每个亚健康状态数据集生成开门和关门亚健康依赖矩阵。

3) 构建基本概率分配函数。将电机与I/O信号测试数据输入到训练好的诊断模型中，得到各自的亚健康初步诊断结果。根据电机数据聚类结果计算特征相似度，利用式(6)构造基本概率分配函数m1。基于I/O信号数据的开门与关门两个贝叶斯推理结果，利用式(7)计算2个基本概率分配结果，并将其进行一次D-S证据融合，将融合后的结果作为基本概率分配m2。

4) 融合诊断。对步骤3)中计算得到的2个基本概率分配函数，根据式(4)的合成规则进行组合，得到车门最终的亚健康概率分配结果m。本文采用信度函数值最大原则进行亚健康判定，诊断的亚健康类型信任度必须为所有信任度的最大值F=max(Bel(Ai))。由于不考虑多种亚健康同时发生的情况，选择BPA最大的亚健康类型作为诊断结果。

3 车门亚健康融合诊断模型应用验证

以广州地铁3号线的塞拉门台架测试数据为例进行验证分析。为了进一步对其亚健康类型进行区分，在台架进行亚健康模拟时，将其细分成11种亚健康类型。采集的数据包含1组正常车门数据，11组不同类型的亚健康数据，每组共包含80条数据(40次开门数据与40次关门数据)。从每组亚健康数据中随机选择60次数据(30次开门数据与30次关门数据)作为1个训练集，剩下的数据作为测试集，生成11个训练集与11个测试集。

3.1 车门亚健康状态识别框架

针对车门出现的11种亚健康类型，确定车门系统的识别框架Θ={f1,f2,…,f11}。表3为车门亚健康状态识别框架。

表3 车门亚健康状态识别框架

3.2 车门亚健康状态初步诊断结果

对正常车门电机数据与未知的测试数据进行聚类分析，主要通过两个指标来判定车门发生的亚健康状态：一是聚类中心与亚健康训练模型，按照第2.3节的方法对特征编号标注“正负号”，正负相反的特征比例要求<0.1；二是相同特征的比例要求≥0.6，当特征相似度超过60%时便认为可能会发生该种亚健康类型。表4为11个亚健康测试集的聚类诊断结果，每种亚健康类型测试集进行5次测试诊断，并对诊断结果取平均值。

根据表4中的诊断结果可以看出，电机数据基于K-means聚类能够对车门亚健康类型进行成功聚类，但是对聚类结果的识别诊断存在不确定性。例如，测试集1、4、5的聚类诊断结果出现了聚类中心，以及两种亚健康模式的特征相似度都超过60%的情况，表明两种亚健康都有可能发生，难以确定车门发生的真实亚健康类型。这种诊断结果不仅体现在同种类型的亚健康之间，测试集1、5的聚类诊断结果给出了两种亚健康模式f1与f5，但是f1为对中尺寸异常，f5为V型尺寸异常，属于不同的亚健康类别。对聚类结果进行模式识别时，如果为了诊断结果尽可能准确而只提高对相同特征的比例要求，则会导致f9、f10、f11出现如f8无法识别的情况；而降低相同特征比例要求则会增加诊断结果的不确定性。

表4 门控器I/O信号的K-means聚类诊断结果

表5为I/O信号的贝叶斯诊断结果。对每个测试样本分配1个预测标签，将分类最多的类别标签作为测试数据的亚健康类型，以分类准确率评估诊断效果。

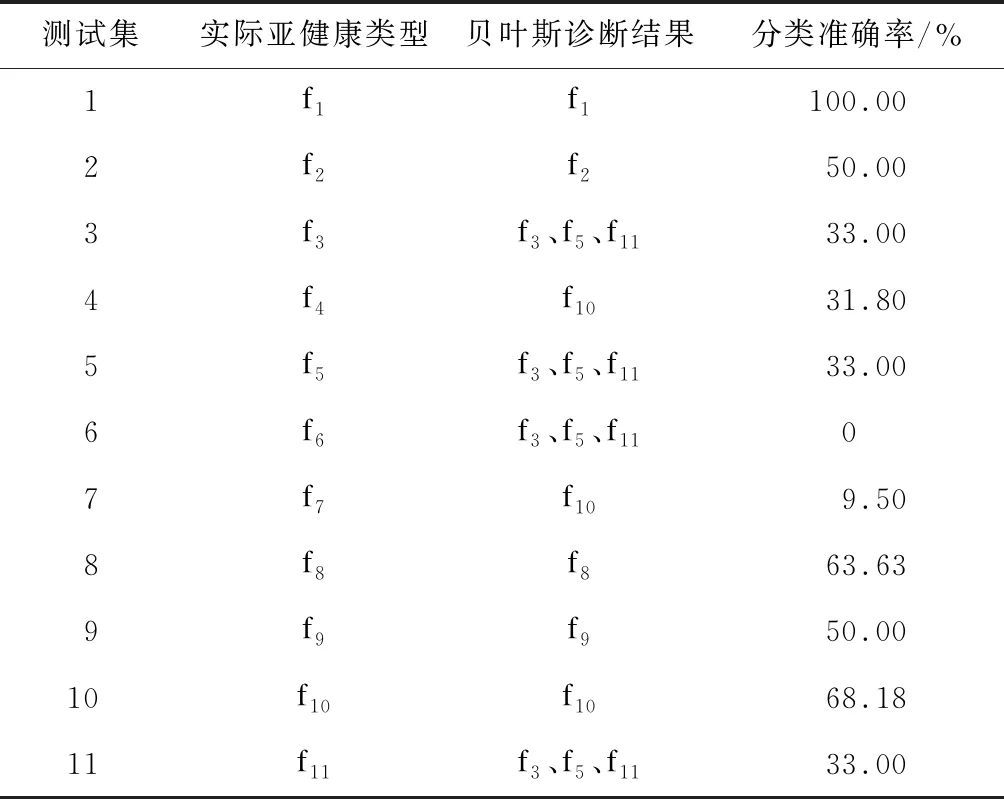
表5 门控器I/O信号的贝叶斯诊断结果

根据表5中的诊断结果看出，I/O信号基于贝叶斯对亚健康诊断的准确率平均值只有42%，不如电机数据诊断结果理想；f3、f5、f11等3种亚健康模式的贝叶斯诊断结果相同且无法进行区分，而f6、f7出现诊断错误情况。导致出现这样结果的原因为：目前城市轨道交通车门门控器采集的可用I/O信号量太少，且多数I/O信号量都与行程开关有关，能够区分的车门状态I/O信息不够全面，后续若能增加I/O数量将会增强其诊断能力。

3.3 车门亚健康状态融合诊断结果

在获取初步诊断结果后，通过式(6)—式(7)分别计算K-means聚类与朴素贝叶斯的诊断结果对亚健康类型的基本概率分配结果，如表6～7所示。

对两个基本概率分配结果利用式(4)的D-S证据合成规则计算融合后得到基本概率分配，并依据信度最大原则确定最终的亚健康类型，诊断结果如表8所示。

表6 基于K-means聚类的BPA计算结果

表7 基于朴素贝叶斯的BPA计算结果

由表6可知，总体上电机数据基于K-means聚类的诊断结果准确性较高，但部分亚健康模型区分特征的差异性不够大，导致亚健康的基本概率分配值较低(0.2～0.4)，整体的诊断结果可靠性较低。表7开关门贝叶斯推理融合后的概率分配结果反映出，I/O信号基于贝叶斯的诊断准确性较差，主要体现在对f3、f5、f11等3种亚健康类型无法区分，但是对f1、f8、f9、f10等4种亚健康类型的诊断置信度较高。

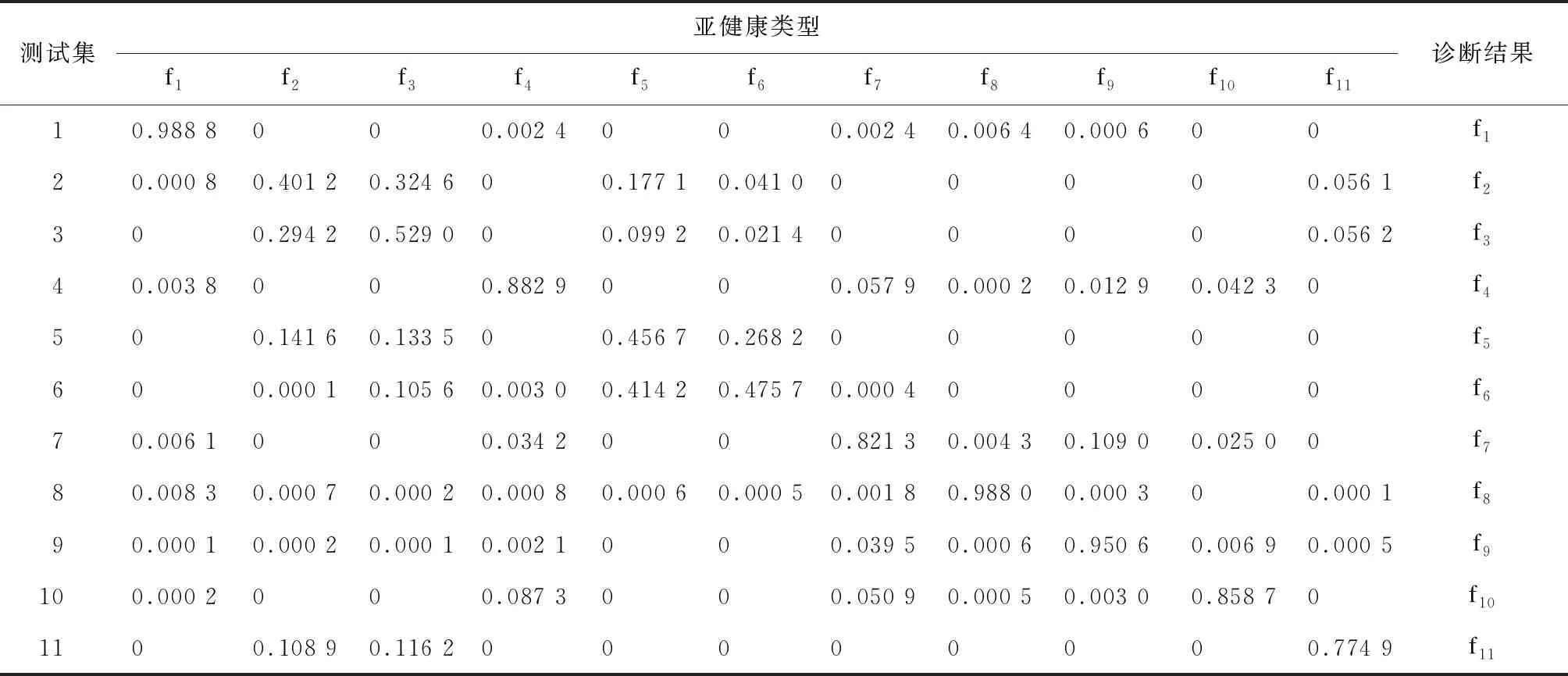
表8 融合诊断基本概率分配结果

根据表8的融合诊断结果可知，融合模型对所有的测试集都能够进行准确诊断。在对测试集进行多次测试后，车门融合诊断模型的诊断准确率达到90%左右。融合后的亚健康诊断模型诊断性能要优于原有的单一诊断模型。与K-means聚类诊断模型相比，融合模型对亚健康的信任度分配更准确、更高而且更加集中，降低了亚健康模式之间的不确定性。与贝叶斯诊断模型相比，融合后的诊断模型能够对识别框架中所有的亚健康类型进行诊断并具有非常高的准确率。由此可见，D-S证据理论能够有效地结合两种诊断模型的优点，弥补互相的不足，提高车门亚健康诊断模型的可靠性与准确性。

4 结语

针对城市轨道交通车辆车门系统在运营过程中处于亚健康工作状态的问题，提出了一种基于D-S证据理论的城市轨道交通车门亚健康诊断方法。该方法能够充分利用车门驱动电机数据与门控器I/O信号数据，并应用K-means聚类与贝叶斯推理的方法构建车门亚健康初步诊断模型。基于D-S证据理论在决策层进行信息融合，实现了车门亚健康状态的多层次、多模型诊断，提高了车门诊断结果的可靠性与准确性。通过车门数据仿真验证表明，本文的融合诊断方法能够充分利用车门可测量数据，弥补单一数据诊断模型的的不足之处，具有实际应用价值。