基于PCA-EWM-TOPSIS耦合算法的地下开采矿山岩体质量分级

刘明淳 蒋加森 姜海涛 陈智斌 谢仁青

摘要：针对传统地下开采矿山岩体质量评价指标之间存在信息冗余的问题，以国内某海下开采金属矿山为例，选用岩石单轴饱和抗压强度、岩体质量指标RQD值、结构面状况等8个指标作为评价指标，采用主成分分析法对评价指标进行降維处理，获得方差累积贡献率达94.873 %的前2个主成分，根据单指标分类区间构造5个岩体质量等级，建立岩体质量评价的EWM-TOPSIS评价模型。研究结果表明：相对传统的可拓评价方法，PCA-EWM-TOPSIS耦合算法对岩体质量分级结果的准确率达88.2 %，评价结果与可拓评价方法评价结果基本一致，且PCA-EWM-TOPSIS耦合算法解决了评价指标过度冗余的问题，大大简化了计算过程，提高了岩体质量评价的效率。该方法具有良好的工程应用价值，可以应用于地下开采矿山岩体质量分级中。

关键词：地下开采;岩体质量分级;主成分分析;PCA耦合;EWM-TOPSIS算法

中图分类号：TD313          文章编号：1001-1277（2022）06-0027-05

文献标志码：Adoi：10.11792/hj20220606

引 言

在地下开采矿山的建设生产过程中，浅部矿产资源已几乎开采殆尽，逐步往深部发展。由于深部围岩的高地应力状态，岩体的破碎现象时有发生，这是岩体稳定性变差的一大诱因。岩体质量分级是评价工程地质条件及围岩稳定性的一项重要手段，是硐室及巷道开挖前的一项重要工作，科学、合理地确定岩体质量分级，可以对开采方式的选择、采场结构参数的优化及支护设计等提供理论指导。

目前，地下工程中应用较为广泛的岩体质量分析方法较多，如传统的RQD法、RMR法和Q分类法单因素评价方法等。近年来，随着计算机科学算法的不断发展，越来越多的综合评价方法被应用于地下开采矿山的岩体质量分级中。例如：尹会永等[1]提出通过有效度修正最大隶属度的方法，建立了改进的熵权-模糊综合评价模型，将其应用于沂南金矿围岩质量分级中，得到了更为科学合理的分级结果，并提出了相应的支护措施;张超等[2]采用分形理论推导出了反映岩体质量等级的分形维数，获得了分形维数与岩体质量之间的量化关系;胡建华等[3]采用指标权重的组合赋权法，对矿山岩体质量评价的物元模型进行了构建，在司家营铁矿岩体质量分级中获得了较好的应用效果;张海磊等[4]提出了岩体质量分级的极限学习机（ELM）模型，评价结果表明，ELM模型具有良好的泛化能力，能够在岩体质量分级中获得准确的结果;郑相悦[5]针对岩体质量的随机性和模糊性，提出了岩体质量分级的变权重-云模型评价方法，获得了与RMR法较为一致的结果;陈顺满等[6]提出了改进功效系数-粗糙集的岩体质量分级模型，并将其成功应用于抽水蓄能电站的地下工程岩体质量分级中;梁桂兰等[7]基于可拓理论，通过熵权法确定指标权重，将熵权-可拓模型应用于坝基岩体质量评价中，效果显著。

以上研究表明，神经网络、模糊数学及分形理论等数学方法被广泛应用于工程岩体质量评价中。在岩体质量评价中，各种数学模型的核心和目的在于将岩体质量评价指标进行聚类处理。地下开采矿山岩体质量综合评价的特点体现在高维度和多指标上，然而，现存的研究结果大多没有对评价指标的相关性进行探讨，多指标权重计算使得评价过程变得复杂，在工程上操作较为繁琐，有些甚至对评价结果影响较大。因此，为解决地下开采矿山岩体质量评价中评价指标信息冗余的问题，本文首先采用主成分分析法（PCA）[8-10]将高维度的原始评价指标进行降维，使之成为少数几个相互独立的综合指标（主成分），同时计算得到每个主成分客观权重，在此基础上，采用耦合熵权、TOPSIS法[11-13]构建地下开采矿山岩体质量的评价模型，为实现矿山岩体质量的精准分级提供技术支持，保证矿产资源的安全生产。

1 PCA-EWM-TOPSIS耦合算法评价模型

1.1 基本原理

主成分分析法计算的核心思想是在保证指标信息不受影响的基础上，通过计算评价指标的特征值及方差累积贡献率，使之成为几个线性独立的综合指标，即主成分;再采用主成分代替原始评价指标，得到主成分矩阵，并将其作为决策矩阵。在获得决策矩阵后，通过TOPSIS法获得各主成分的欧氏距离。最后，计算待评价对象的欧氏距离，对主成分矩阵进行合理排序，确定待评价指标的等级。

1.2 评价模型的构建

1） 评价数据的标准化处理。采用标准差标准化方法对待评价数据进行标准化处理，计算公式为：

y ij=x ij-min（x ij）jmax（x ij）j-min（x ij）j，越大越好的指标

y ij=max（x ij）j-x ijmax（x ij）j-min（x ij）j，越小越好的指标（1）

式中：y ij为第i个评价对象第j个指标标准化处理后的值;x ij为第i个评价对象第j个指标的初始数据;min（x ij）j为第j个评价指标中的最小值;max（x ij）j为第j个评价指标中的最大值。

2） 标准化数据的主成分分析。通过主成分分析法，获得各指标特征值及方差累积贡献率，确定主成分及主成分矩阵。主成分矩阵转化为特征向量矩阵，其表达式为：

Y i1=b 11y i1+b 12y i2+…+b 1jy ijY i2=b 21y i1+b 22y i2+…+b 2jy ij

Y ik=b k1y i1+b k2y i2+…+b kjy ij

（2）

式中：Y ik为第i个评价对象的第k个主成分;b kj为第k个主成分第j个指标的特征变量;y ij为第i个评价对象第j个指标标准化处理后的值（i=1，2，…，m;j=1，2，…，l）。

确定各主成分贡献率，计算公式为：

w k=a k/∑lk=1a k（3）

式中：w k为第k个主成分的贡献率;a k为第k个主成分的方差贡献率;∑lk=1a k为所抽取主成分的方差累积贡献率，根据方差累积贡献率将权重较小的主成分剔除，一般取方差累积贡献率达85 %以上的主成分组成主成分矩阵A。

3） 基于熵权法（EWM）的权重计算。将主成分矩阵A作为待评价矩阵，基于EWM法确定待评价指标（新形成的主成分）的权重。其步骤一般为：

计算第j个指标的信息熵（S（d j））和输出熵（C（d j）），即

S（d j）=-∑mi=1y ijln y ij

C（d j）=S（d j）ln m（4）

计算得到第j个指标的差异系数（H（d j））：

H（d j）=1-C（d j）（5）

第j个指标的权重W j为：

W j=H（d j）∑nj=1H（d j）（6）

则评价指标的权重向量为：W=（W 1，W 2，…，W n）。

4） 通过对主成分矩阵A赋权获得加权后的矩阵B，有：

B=（b ij） m′n=（W jY ij） m′n（7）

5） 確定每个主成分的正、负理想解r+ ik和r- ik。确定不同评价对象与正、负理想解的欧式距离d+、d-，以及相对贴近度T i。

d+=∑lk=1（r ik-r+ ik）2

d-=∑lk=1（r ik-r- ik）2 （8）

T i=d- id+ i+d- i（9）

2 地下开采矿山岩体质量评价体系的建立

对岩体质量进行综合评价是矿山企业安全高效开采的前提，而评价体系的建立对岩体质量评价结果的合理性与准确性有着直接的影响。在整个评价指标体系中，各因素既有联系，又存在相互制约的关系。因此，首先选取几个评价指标，再采用PCA法进行降维处理，可以有效降低评价指标之间的信息冗余，全面反映岩体质量评价所需要的信息。

在矿山实际生产过程中，一般以岩体的物理力学参数、结构面特性及地下水状态等影响工程岩体稳定性的因素作为岩体质量评价的指标。具体来说，在相关理论及实际研究中，影响地下开采矿山岩体质量的因素概括起来有完整岩石的物理力学参数、岩体的完整程度、岩体的结构面性质、岩体赋存环境及采动影响因素5大类。考虑到评价指标的量化问题，本文选取岩石单轴饱和抗压强度（R c）、岩体质量指标RQD值、结构面状况（J f）、节理间距（J d）、完整性系数（K v）、地应力影响系数（Q）、地下水状态（W）、爆破开挖扰动系数（D）等8个指标作为评价指标。根据以往岩体质量分级结果及相关国家、行业规范和标准，将地下开采矿山岩体质量分为5个等级（见表1），即Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ。

3 工程应用实例

3.1 工程背景

以国内某海下开采金属矿山为工程背景。近年来，随着浅部矿产资源开采殆尽，该矿山逐渐转向深部开采。由于深部“三高一扰动”的影响，岩体所受地应力增大，岩体的完整性随之变差，岩体的稳定性也越来越差，导致工作面周围经常出现顶板冒落、片帮等一系列工程问题，部分区域甚至出现了岩爆现象，严重影响矿山深部的安全生产。

为了实现矿山的有序生产，首先必须对矿区岩体进行准确评价，再根据岩体质量等级对矿山开采方案进行选择，确定合理的采场结构参数，以确保矿山资源的安全、高效、经济开采。

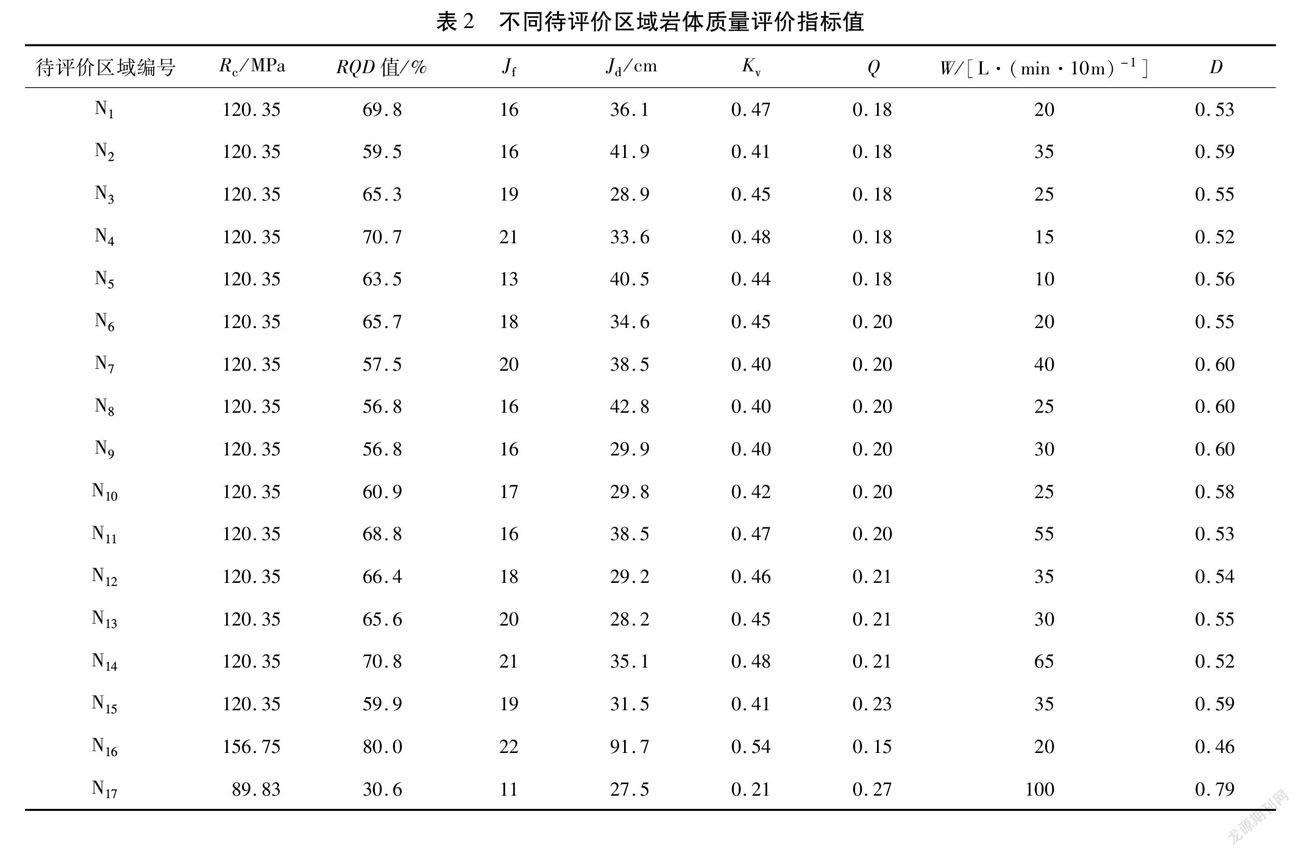
围绕矿山岩体质量评价体系的建立，以该矿山直属矿区为工程背景，在矿区岩体室内试验和现场调查的基础上，确定各待评价区域的岩体质量评价指标值，结果见表2。

3.2 岩体质量评价指标的主成分分析

将表1中各等级的临界值与表2中的待评价指标值相结合，作为一个完整决策矩阵，标准化后通过SPSS软件进行决策矩阵的主成分分析，得到主成分方差贡献率碎石图（见图1），通过计算分析得到8个成分的方差贡献率分别为82.956 %、11.917 %、2.942 %、1.214 %、0.547 %、0.377 %、0.071 %及0.017 %，抽取前2个主成分，其方差累积贡献率达到了94.873 %，能够全面反映原始指标所包含的信息。

用2个主成分代替原有的8个评价指标，经过线性变化，主成分矩阵计算公式为：

Y i1=0.144y i1+0.145y i2+0.144y i3+0.115y i4+

0.148y i5+0.126y i6+0.127y i7+0.145y i8

Y i2=0.19y i1+0.129y i2+0.072y i3+0.064y i4+

0.166y i5+0.050y i6+0.051y i7+0.212y i8（10）

通过式（10）的线性变化后，获得标准化待评价区域的主成分决策矩阵，结果见表3。

3.3 熵权法确定指标权重

采用式（4）～（6）计算表3中标准化的主成分决策矩阵权重，获得主成分评价指标权重值，结果见表4。

3.4 主成分评价指标正、负理想解矩阵确定

在进行主成分分析时，各评价指标都进行了归一化处理，根据表1及式（4），可以确定表3中主成分评价指标的分级标准范围（Ⅰ～Ⅴ），获得的2个正、负理想解矩阵分别为：

3.5 评价结果分析

根据所建立的主成分矩阵进行EWM-TOPSIS模型评价，获得各待评价区域的岩体质量评价结果，见表5。以待评价区域N 1为例，通过式（7）～（9）计算得到的评价指标到各等级理想解贴近度为T Ⅲ>T Ⅳ>T V>T Ⅰ>T Ⅱ，判断N 1的岩体质量等级为Ⅲ级，其他以此类推。由表5可知，本文采用的PCA-EWM-TOPSIS耦合算法，相比可拓评价方法评价结果，除个别待评价区域结果有所出入外，其余评价结果基本与可拓评价方法评价结果保持一致，准确率高达88.2 %。

因此，本文采用的评价模型与可拓评价方法计算结果非常吻合，由此可以认为，PCA-EWM-TOPSIS耦合算法评价结果是准确可靠的，该评价方法是行之有效的。虽然本文采用方法与可拓评价方法评价结果存在微小的差异，但是对整体的评价结果影响不大。另外，采用主成分分析法对原始评价指标进行降维处理，消除了冗余信息，在不影响评价结果的基础上，大大降低了繁琐的计算过程，相比其他评价方法，提高了整体的计算效率，不失为一种有效的地下工程岩体质量评价方法。

4 结 论

本文提出了地下矿山岩体质量评价的PCA-EWM-TOPSIS耦合算法评价模型，并在国内某海下开采金属矿山进行了应用，取得如下结论：

1） 针对传统岩体质量评价指标之间的信息冗余，在8个评价指标的基础上，提出采用PCA法对原始评价指标进行降维处理。计算得到前2个主成分方差累积贡献率为94.873 %，能够较好地反映岩体质量等级信息。

2） 采用EWM计算方法进行主成分评价指标的权重计算，保证了评价指标权重获取的科学性与客观性。

3） 利用TOPSIS方法对赋权后的决策矩阵进行正、负理想解贴近度的计算，充分挖掘待评价样本间的内在规律，获得了与可拓评价方法较为一致的结果，准确率达88.2 %。本文采用的PCA-EWM-TOPSIS耦合算法评价模型，最大限度地消除了评价指标的数据冗余，大大简化了数据处理及计算过程，而结果与传统评价方法却无显著差异，验证了该方法的准确性及有效性，为地下开采矿山岩体质量评价提供了新思路。

[参 考 文 献]

[1] 尹会永，赵涵，徐琳，等.岩体质量分级的改进模糊综合评价法[J].金属矿山，2020（7）：53-58.

[2] 张超，宋卫东，付建新.分形理论在岩体质量评价中的研究[J].矿业研究与开发，2020，40（2）：75-79.

[3] 胡建华，艾自华.基于最优组合赋权的地下矿山岩体质量可拓评价模型[J].黄金科学技术，2017，25（4）：39-45.

[4] 张海磊，严文炳，郭生茂，等.基于ELM模型的岩体质量分级及应用[J].黄金，2018，39（12）：36-38，42.

[5] 郑相悦.基于变权重-云模型的岩体质量评价方法[J].现代矿业，2018，34（7）：88-90，95.

[6] 陈顺满，吴爱祥，王贻明，等.基于粗糙集和改进功效系数法的岩体质量评价[J].华中科技大学学报（自然科学版），2018，46（7）：36-41.

[7] 梁桂兰，徐卫亚，谈小龙.基于熵权的可拓理论在岩体质量评价中的应用[J].岩土力学，2010，31（2）：535-540.

[8] 陈绍杰，刘久潭，汪锋，等.基于PCA-RA的滨海矿井水源识别技术研究[J].煤炭科学技术，2021，49（2）：217-225.

[9] 黄楠，郑禄林，左宇军，等.基于PCA-Fuzzy-PSO-SVM的巷道围岩稳定性评价[J].矿业研究与开发，2020，40（12）：75-80.

[10] 刘晓光，刘爽，李柯.PCA-聚类分析在煤与瓦斯突出预测中的应用研究[J].煤炭技术，2017，36（6）：166-168.

[11] 卢富然，陈建宏.基于AHP和熵权TOPSIS模型的岩爆预测方法[J].黄金科学技术，2018，26（3）：365-371.

[12] 魏杰，李全明，褚衍玉，等.基于EWM-TOPSIS模型的房柱式采场布置方案优选研究[J].合肥工业大学学报（自然科学版），2021，44（5）：691-695.

[13] 王石，徐磊，柯愈贤，等.基于最优组合权重的GRA-TOPSIS深井巷道支护方案优选[J].重庆大学学报，2019，42（6）：78-87.

Rock mass quality grading of underground mining mine based

on PCA-EWM-TOPSIS coupled algorithm

Liu Mingchun，Jiang Jiasen，Jiang Haitao，Chen Zhibin，Xie Renqing

（Fujian Geotechnical Engineering Investigation and Research Institute Co.，Ltd.）

Abstract：In view of the problem of information redundancy between traditional quality evaluation indicators of underground rock mass，8 indicators，such as the uniaxial saturated compressive strength of rocks，the RQD value of quality indicators of rock mass，and the status of structural planes，are selected as evaluation indicators for an undersea metal mine in China.The first 2 principal components with a variance cumulative contribution rate of 94.873 % are obtained by dimensionality reduction of the evaluation indexes using principal component analysis （PCA），and 5 rock mass quality grades are constructed based on the single index classification interval to build an EWM-TOPSIS evaluation model for rock mass quality evaluation.The results of the study show that the PCA-EWM-TOPSIS coupled method achieves 88.2 % accuracy for the quality grading results of rock mass with respect to the traditional topological assessment method，and the evaluation results basically agree with the evaluation results of the topological assessment method，and the PCA-EWM-TOPSIS coupled method solves the problem of the over-redundancy of the evaluation indexes，greatly simplifying the calculation process and improves the efficiency of the quality evaluation of rock mass.The method has good engineering application potentials and can be applied to underground rock mass quality grading.

Keywords：underground mining;rock mass quality grading;principal component analysis;PCA coupled;EWM-TOPSIS algorithm

收稿日期：2021-12-13; 修回日期：2022-02-15

基金項目：国家自然科学基金项目（12005099）

作者简介：刘明淳（1988—），男，福建闽侯人，工程师，从事矿山岩土工程勘察、设计、施工等方面的研究工作;福州市闽侯县上街镇海西科技园科技东路1号中国冶金地质总局二局3楼，福建岩土工程勘察研究院有限公司，350001;E-mail：568292871@qq.com