基于拉格朗日方程导出的三模耦合模理论及实验验证

张亚博，丁中正，彭雪城，黄万霞，黄时中

(安徽师范大学 物理与电子信息学院 安徽省光电材料科学和技术重点实验室，安徽 芜湖 241002)

引言

振动是物体或质点在其平衡位置附近所做有规律的一种往复运动，分为理想振动和非理想的振动，两者最大区别就是有无阻尼的存在。机械的振动中有代表性的简谐运动便是最基本最简单的机械振动，被用来分析简谐振动的是物理学中的经典弹簧振子模型[1-2]以及拉格朗日方程[3]。相比于经典的弹簧振子模型，拉格朗日函数是由动能和势能组成而且具有非唯一性[4]，更容易推广到其它学科。但是由于拉格朗日函数代入到拉格朗日方程中，给出的微分方程仍然是时间的二阶微分方程(即弹簧振子模型)，求解比较复杂。因此在各领域的研究中常用耦合模理论(Coupled Mode Theory:CMT)[5-6]，来解释两个或多个模式之间相互作用。CMT由Pierce和Miller于1954年首次提出，最初该理论仅用来解释微波波导与无源器件性质,后来在众多研究者的推动下，可以方便的描述光学非线性，光波、声波相互作用等波动现象的一般规律，并且具有物理概念直观且数学形式简洁、效率高且较为准确的优点。CMT被很好的用来解释各种各样的奇异现象，如电磁诱导透明(Electromagnetically Induced Transparency:EIT)[7]、Fano共振[8]、奇异点(Exceptional Point:EP)[9-10]、连续域束缚态(Bound States in the Continuum:BIC)[11]等现象。正是由于这些奇异现象的重要应用前景，如光子晶体中的慢光[12]、非线性耦合[13]、耦合谐振器传感[14]、磁共振耦合无线能量传输[15]等，使得CMT获得越来越多学者的青睐。近年来，CMT在光学研究方面的表现尤为突出，借助于CMT来描述光波导模式之间的相互作用，是光波导器件分析中常用的理论分析方法[16-17]，被广泛应用于涉及模式耦合的诸多领域,比如有光栅的导模共振[18]，微纳光子学中波导与微腔的耦合[19],光子晶体微腔共振[20],多纳米颗粒组合[21]等都有很大的拓展应用。如在纳米光学体系中，多个光子共振体间耦合引起了人们的广泛关注。相对于单一光子共振结构体系，由多个光子共振体组成的复杂耦合体系有着更大的调控自由度和更令人着迷的现象。相比目前在实验方面取得的进步，对于耦合问题的理论描述仍远未令人满意。2021年林婧[22]等人利用CMT，从光子共振体封闭体系到开放体系，系统介绍了处理共振体间耦合的理论工具，以及如何利用这些工具设计具有特定电磁波调控功能的新型超构表面，提供了一套强大工具用于理解并调控多共振体间的耦合行为，为设计可掌控的耦合光子系统提供了可能。

文献[1-2]通过久期微扰理论将弹簧振子模型退化到CMT，很好地解释了两个音叉的耦合谱线，可是由于交叉耦合系数在以往的研究公式中都以平方形式出现，无法确定交叉耦合系数的正负号。在本文中，从拉格朗日函数出发，建立了三模耦合拉格朗日方程，结合久期微扰理论，将拉格朗日方程退化为CMT，并且严格给出了各物理量的意义。为了验证理论的正确性，分别实验探究了单音叉耦合、双音叉耦合、以及三音叉振动属性，理论很好地解释了谱线。这些研究为将CMT正确推广到其它领域具有一定的指导意义。

1 耦合理论

三个音叉两两用弹簧连接，如图1所示。设mα,xα,Γα以及ωα(α=p,q,n)为第α音叉的等效质量、相对平衡位置的偏移、总损耗和固有频率。其中连接弹簧的劲度系数分别为kpq和kqn。不失普遍性，假定低频信号源为音叉p提供周期性的驱动力Gcos(ωt)，ω为源频率，且探测器也与音叉p相连，如图1(a)所示。则该体系的拉格朗日函数为[23]

该体系的耗散函数F为

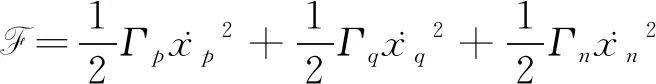
(2)

代入耗散体系的拉格朗日方程

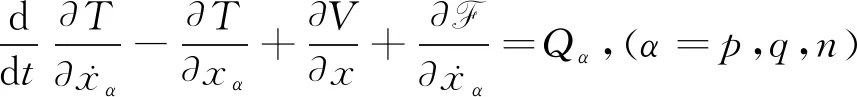
(3)

则该耦合体系的动力学方程为

上面三个方程组是二阶常系数常微分方程组，即为文献[2]中所说的弹簧振子模型，弹簧振子模型在久期微扰理论近似下可以退化一阶微分方程组的CMT中的主方程，为了推导方便我们假设三个音叉的等效质量相等，即：mp=mq=mn=m，在推导过程中，选取ω0∈{ωp,ωq,ωn}为频率参考点，经过推导得到三个音叉耦合的主方程为

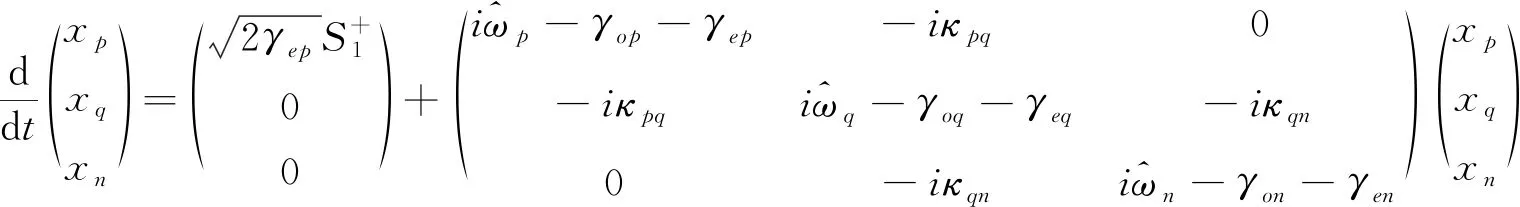
(5)

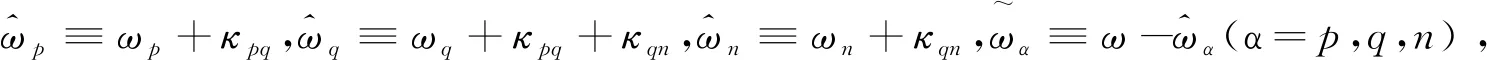
图1 三音叉耦合体系结构示意图；(a)p模与输入和输出端相连；(b)q模与输入和输出端相连；(c)n模与输入和输出端相连

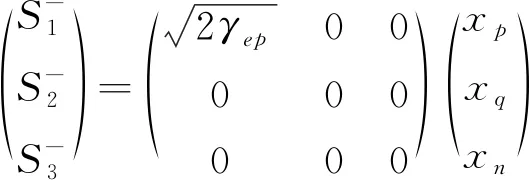
(6)

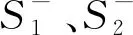
(7)

由方程(7)可得

将式(8)代入式(7)，可得

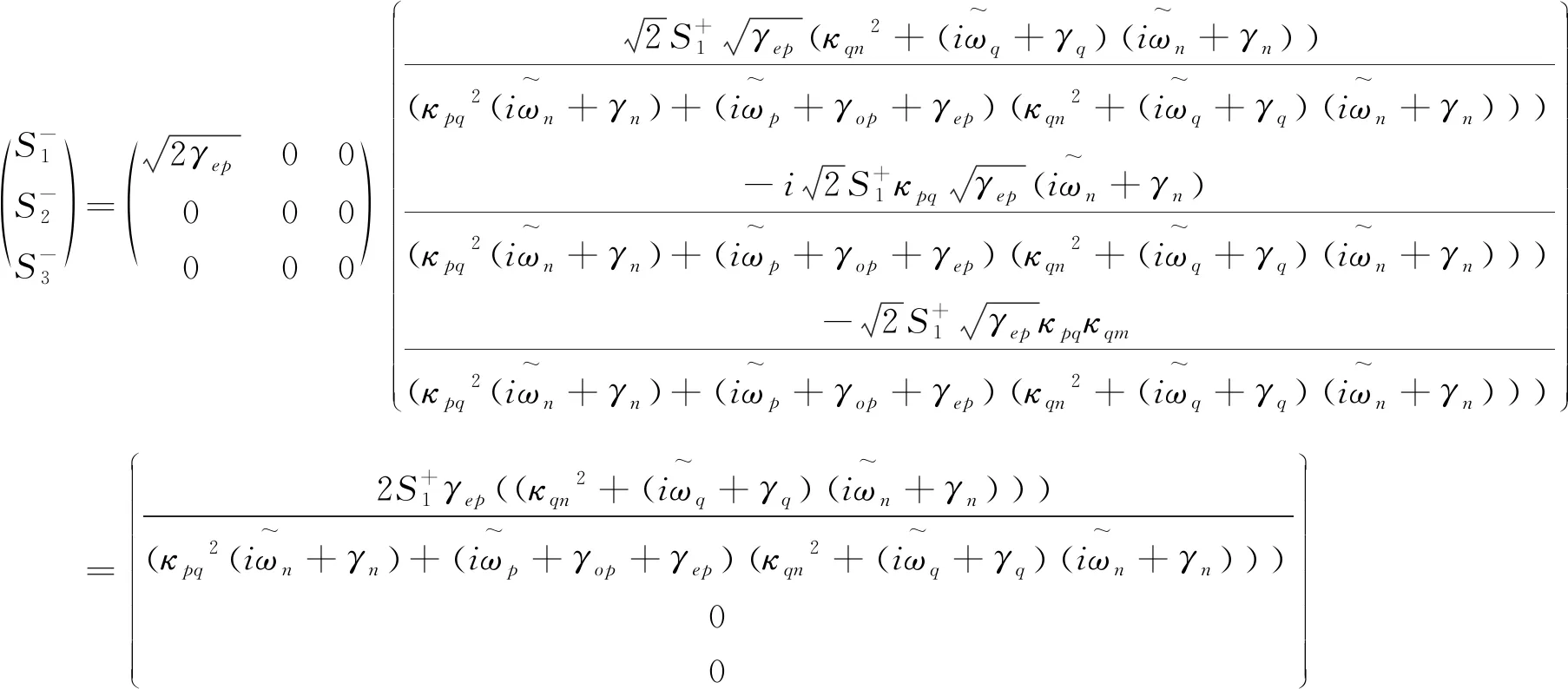
(9)

则探测器检测到的振幅谱为

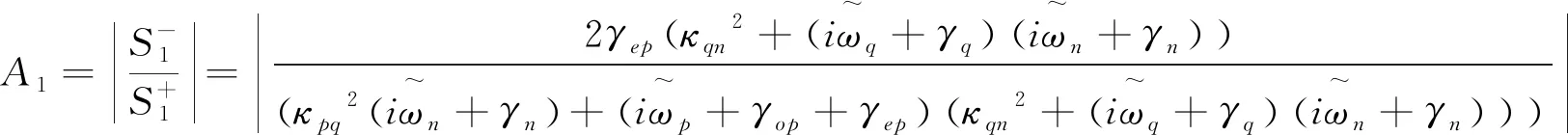
(10)

讨论：1)如果κqn=0时，公式(10)简化为

(11)

此时的A1公式中只含有关于p，q模的参数，退化成两模耦合的振幅谱。

2)κqn=0和κpq=0同时成立时，公式(10)退化为

(12)

此时的A1公式中只含有p模的参数，退化成无耦合的单模振幅谱。定义音叉的传输效率η为振幅的平方，即

(13)

同理，当外界驱动信号和探测系统都加载在第q个模式(中间音叉)上时，如图1(b)所示，则动力学方程为

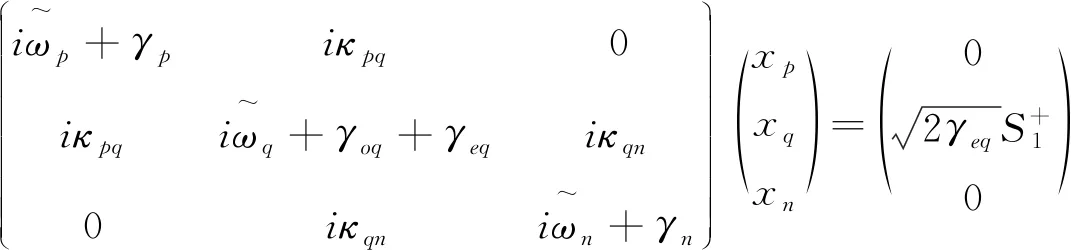
(14)

则

(15)

测量的振幅谱为

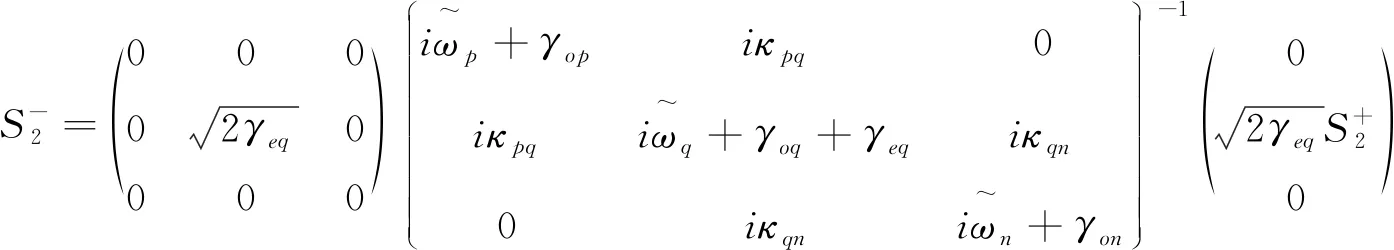
(16)

(17)

同理，当外界驱动信号和探测器连接在第n个模上，如图1(c)所示，这种情况与第一种情况类似。

另一方面，如果没有外界输入，则方程(7)简化为

(18)

其中当模式不与传输线相连时，相应的传输损耗为零。方程(18)是体系的本征方程，要使上式有非零解，则系数行列式为零

(19)

可以得到体系的三个本征值。由于一元三次方程的求根公式比较复杂，在此我们主要讨论以下三种情况：

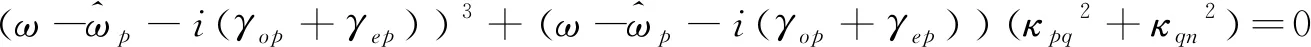
(20)

则三个本征复圆频率为

式(21-a)-(21-c)的实部为杂化模的本征圆频率，三个相同模式耦合，得到三个不同的本征圆频率。其中一个杂化圆频率与没有耦合的音叉固有圆频率相同，另外两个，一个高于原固有圆频率，另一个低于原固有圆频率。

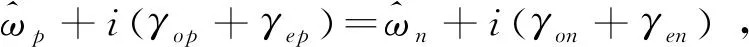
(22)

解得三个本征复圆频率为

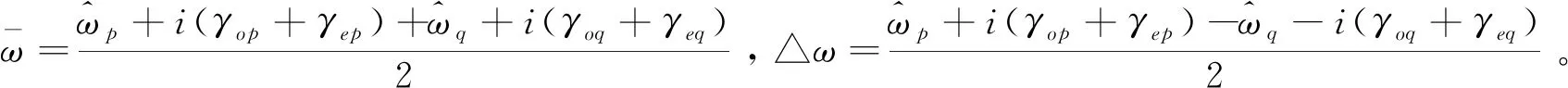
3)若只有两个模式耦合，即κqn=0，方程(19)就退化为

(24)

由方程(24)可得

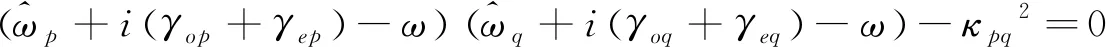
(25)

方程(25)两个根分别为

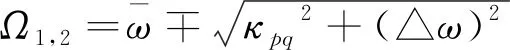
(26)

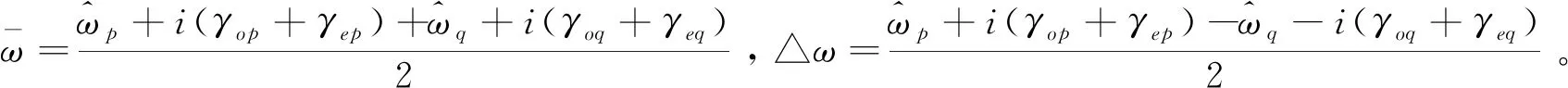
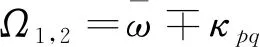
(27)

即杂化后的本征模式一个高于两个模平均的固有频率，一个低于两个模平均的固有频率。

2 实验验证

为了验证CMT理论的正确性和系统地研究三音叉耦合的属性，分别搭建单个音叉(图2(a))、两音叉(图2(c))以及三音叉(图3((a)、(c)和(e)))耦合实验装置，并且分别测量了每个音叉单独存在时的振幅谱、两个音叉耦合振幅谱以及三个音叉耦合谱。

2.1 单模实验和理论解释

单个音叉的实验装置如图2(a)所示，图2(b)为单个音叉的相应振幅谱，其中红色菱形、黑色三角以及紫色圆点分别为音叉F1，F2以及F3的实验谱，红色实线、黑色虚点以及紫色虚点线为拟合谱，两者谱线吻合较好，证实方案可行，得出了每个实验音叉的共振频率：F1、F2以及F3的共振频率为243.45Hz，244.45Hz，246Hz。音叉的品质因子Q一般定义为

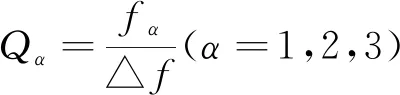
(28)

2.2 双模耦合实验和理论解释

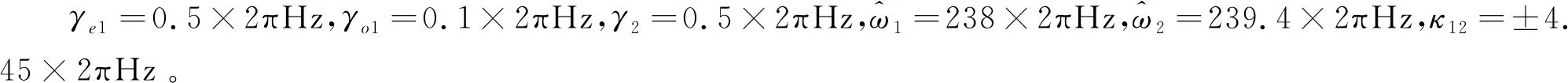
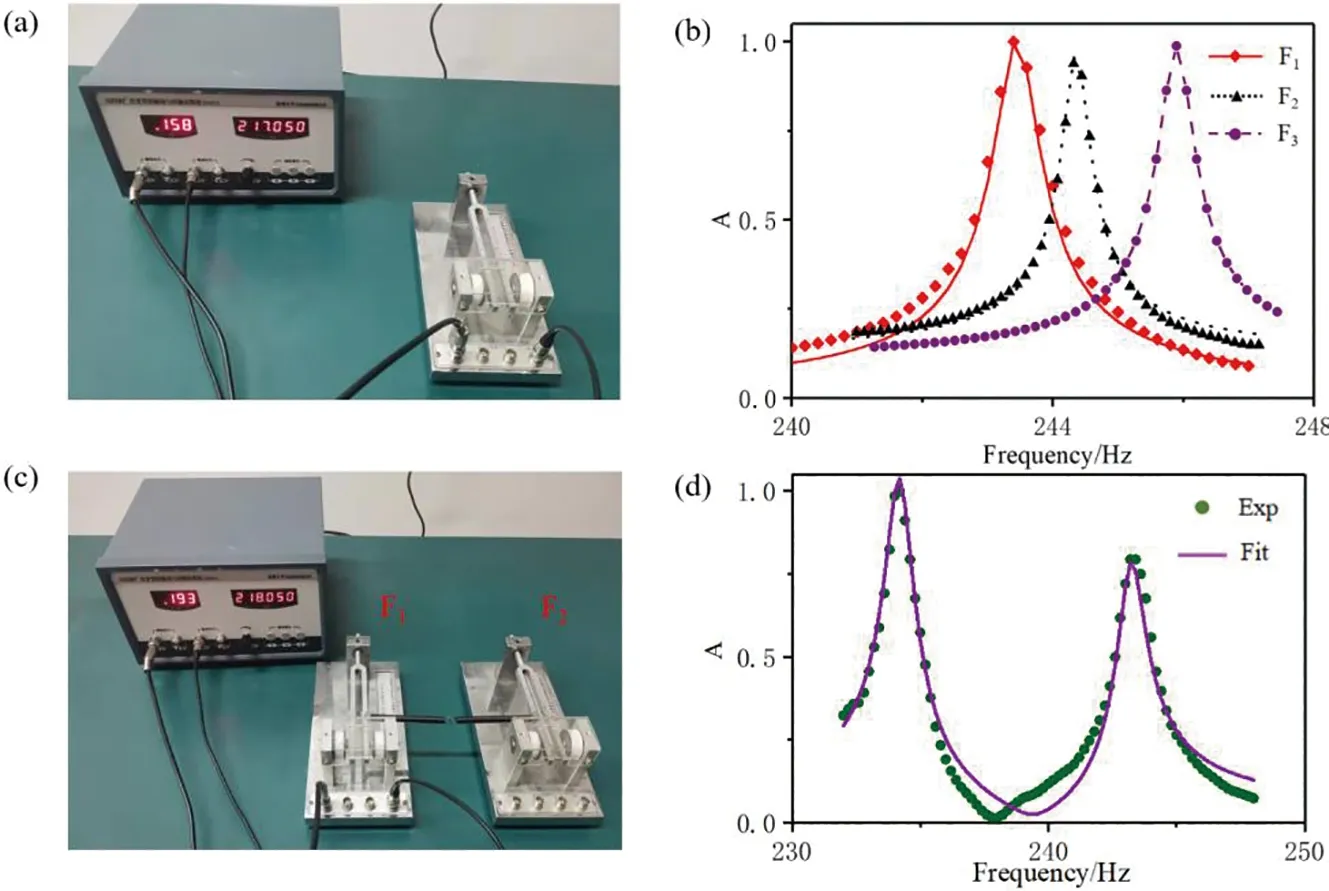
图2 (a)单模实验装置图；(b)单模振幅谱；(c)双模耦合实验装置图；(d)双模耦合振幅谱

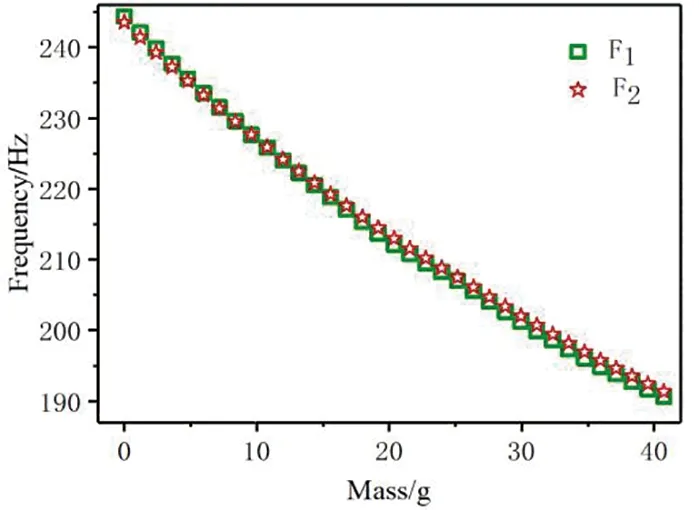
图3 音叉共振频率与音叉臂增加质量的关系Fig.3 Tuning fork resonance frequency versus increased mass of tuning fork arm

2.3 三模耦合实验

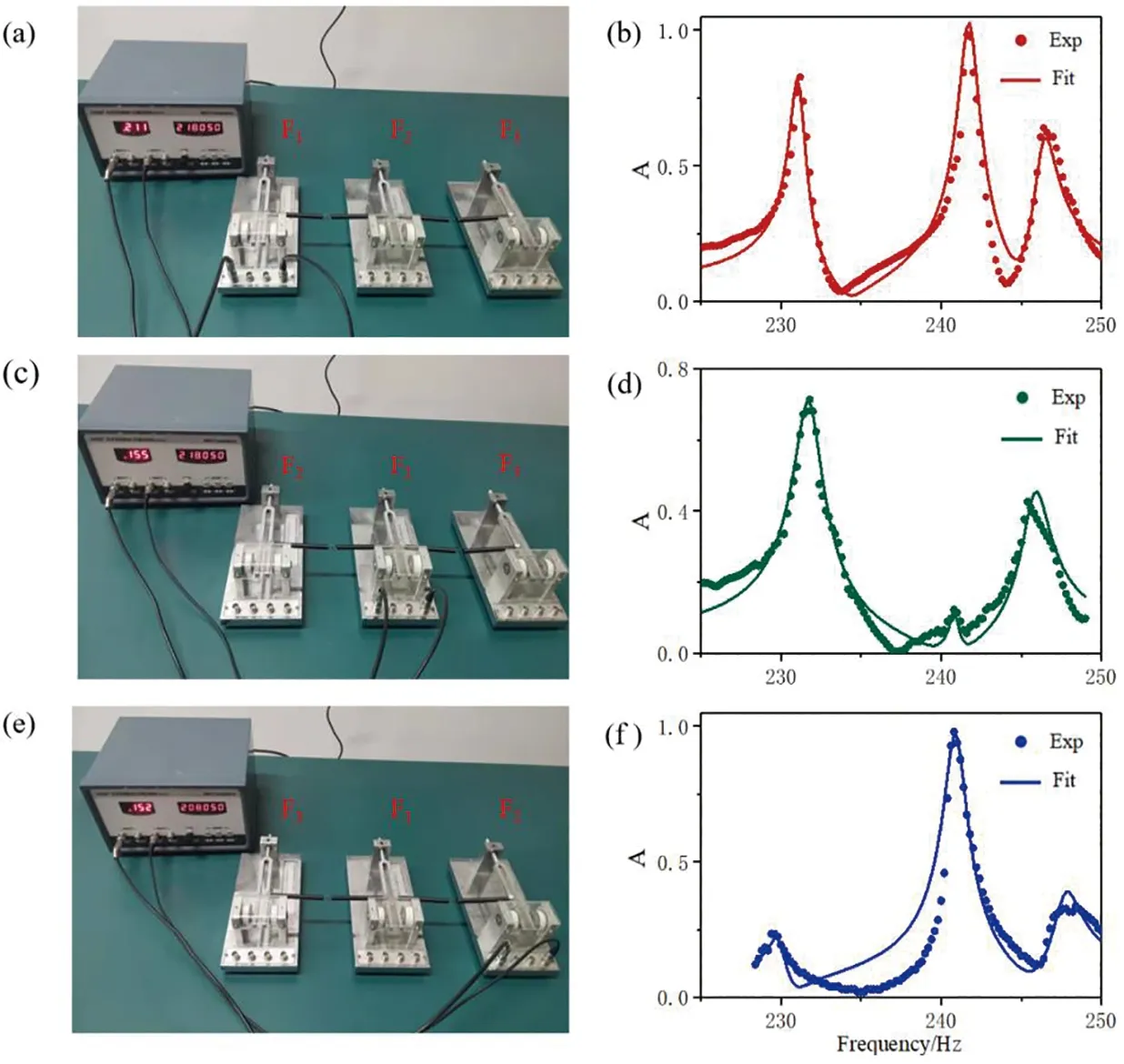
图4 (a)为F1,F2,F3按顺序排列，输出端和输入端都接在F1；(b)为它的振幅谱；(c)为F2,F1,F3按顺序排列，输入端和输出端都接在F1；(d)为它的振幅谱；(e)为F3,F1,F2按顺序排列，输出端和输入端都接在F2；(f)为它的振幅谱Fig.4 (a) F1,F2,F3 are arranged in order,both the output and input terminals are connected to F1;(b) is its amplitude spectrum;(c) F2,F1,F3 are arranged in order,both the input and output terminals are connected to F1;(d) is its amplitude spectrum;(e) F3,F1,F2 are arranged in order,and both the output and input terminals are connected to F2;(f) is its amplitude spectrum.

3 应用推广

在纳米光学体系中，当单胞由纳米颗粒组成的超构表面，衬底为玻璃，其折射率为n。如果纳米颗粒同时包含两个模式，一个亮模和一个暗模，当结构对称破缺时，这两个模式发生耦合，描述两个光学模式耦合的的动力学方程就可以用CMT来描述。例如文献[17,29]中，单胞为带有方形空的矩形纳米颗粒，如图5所示。当结构完全对称时，这个结构在我们感兴趣的波段既有一个偶极子p又有一个四极子q。偶极子可以看成亮模，四极子可以看成暗模，当结构对称破缺时，亮模和暗模的相干叠加导致非对称线型，即Fano共振。

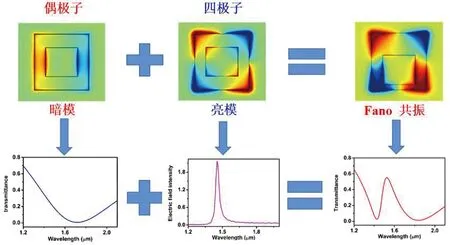
图5 偶极模和四极模干涉引起的Fano共振Fig.5 Fano resonance caused by dipole mode and quadrupole mode interference

描述这种现象的CMT主方程可以写为

(29)

出射波的表达式为

(30)

由上式推导可得复透射系数

(31)

4 结论

本文从拉格朗日方程出发，建立了更完善的音叉耦合系统的动力学方程，再利用久期微扰理论将动力学方程退化为CMT的主方程，搭建的音叉耦合实验很好地验证了我们的理论，在实验中通过改变音叉耦合实验中一些的参数，对共振峰的位置，大小，品质因子的大小，都会带来不同的结果，而对于三模耦合系统较双模耦合系统有更多的可调参数，因此在实际应用中带来更多可能性，该理论在研究机械耦合、光机械耦合等方面有一定的指导意义。