基于改进A*算法的飞行器航迹规划

秦钰彧，夏丰领，黄国勇，2

（1.昆明理工大学 信息工程与自动化学院，云南 昆明 650504；2.昆明理工大学 民航与航空学院，云南 昆明 650504）

0 引言

飞行器航迹规划是指综合考虑飞行器机动性能、突防概率、碰地概率及飞行时间等约束因素，寻找一条从起始点到目标点的最优或可行的飞行轨迹[1]。航迹规划问题作为一个复杂的优化问题，需要高效的算法来进行求解。但随着问题复杂度的增加，传统算法往往存在过快陷入局部最优解、迭代过慢等问题[2]。传统的A*算法虽然是基于静态图最有效的直接搜索算法，但在规划区域栅格化后，节点扩展只限于栅格线的交叉点，存在无效转折，因此路径长度不是最短，实际规划出的是次优路径。近些年，一些新兴的群智能元启发式算法相继被提出，如灰狼算法（Grey Wolf Optimizer，GWO）、粒子群算法及遗传算法等。RAM 等[3]将GWO 算法的性能与蚁群算法（Indicator Based Ant，IBA）、粒子群算法（Particle Swarm Optimization，PSO）、鲸鱼算法（Whale Optimization Algorithm，WOA）以及正余弦算法（Sine Cosine Algorithm，SCA）等启发式算法进行了比较，在轨迹规划中，GWO 算法的性能比其他启发式算法更好。魏燕明等[4]采用灰狼优化算法对军用运输机进行航路规划，并与Dijkstra 算法和Floyd 算法进行对比，证明了GWO 算法能很好地完成航路规划的求解，但未对避障规划能力进行深入研究。虽然灰狼优化算法具有控制参数少、能在一定程度上避免陷入局部最优等优点，但是灰狼优化算法初始化时也存在问题：随机初始化个体后生成的航点杂乱无序，造成个体的适应度比较低，更新策略不灵活。TOO 等[5]提出了二进制灰狼算法（Binary Grey Wolf Optimizer，BGWO），优化了灰狼算法的搜索方法，使更新策略更加灵活。针对智能算法的初始值多采用随机生成方式，导致算法的收敛速度降低、算法运行时间较长的问题，实际应用中，将经典算法与智能算法进行融合形成融合算法，取得较好的效果以及得到更优解的同时，能加速算法收敛。黄辰等[6]通过使用A*算法取代蚁群算法的信息素随机初始化过程，增加了蚁群算法的稳定性；曹建秋等[7]提出了一种基于A*初始化的变异灰狼优化算法解决无人机任务规划问题，但狼群初始化后只能找到无威胁约束域下的可行解，需配合修正变异来进一步优化。针对A*算法节点扩展时存在的局限性，Theta*算法[8]在A*算法的基础上加入了可视化检查机制，使得转折角度更丰富，但频繁可视化检查会带来难以忽视的计算成本，因此总的搜索效率会因地图复杂而降低；而张帅等[9]采用圆形节点扩展方法，使节点实现变方向和变步长形式扩展，但随着规划精细化，搜索效率大幅度降低。

A*算法作为全局搜索算法，可以把握大局，确保能够找到可行的航线。结合二进制灰狼算法，可打破A*算法节点扩展时带来的转弯角度局限，并通过缩减航迹点来缩短航程。本文提出了一种基于改进A*（A*-BGWO）算法的飞行器航迹规划方法，通过A*算法在离散化的地图上求取一个较优的初始矩阵，随后通过二进制灰狼优化算法构建和更新种群，得到最优航迹点集合。该算法规划出的航迹能在准确避开多个障碍物的同时，减少多余航迹点从而最缩短航程，优化转弯角度。

1 环境模型

本文首先对三维地理环境进行离散化处理。通过对规划空间进行栅格划分，将规划空间划分为大小相等、彼此相邻的立方体，在规划空间搜索多个有序的飞行航迹点，从起点依次连接到目标点，形成航迹。

规划时，本文将威胁区及其领空视为禁飞区，规划为统一的威胁模型，并用等效地形来近似模拟。由于还需考虑飞行器与实际威胁区域之间的安全距离以及飞行器转弯半径，因此在栅格地图上对威胁区进行膨胀处理，扩大威胁模型，并允许搜索的航迹通过障碍栅格的顶点。

地图离散化后，该矩阵的第i行j列元素代表该精度下该节点的海拔高度hij，设该规划段的最小飞行高度为hmin，于是设置hmin为安全海拔。威胁区的威胁模型高度设置为高于安全海拔的数值，威胁较小的安全区域作为地形模型，该区域高度设置为安全海拔以下的数值，海拔越高，模型颜色设置越浅。

2 评价函数

为使飞行器能避开威胁区的同时，避免频繁调整航向和姿态，需要达到的效果为：在无威胁的自由空间，航迹搜索的航迹点间隔较大，避免无效转折，缩短航程；在接近威胁区域时，确保飞行器飞行时能成功规避威胁的同时，转弯角度不易过大，避免频繁转向。因此，本文将飞行时间代价、威胁代价及转弯角度代价进行线性加权，其和作为对航迹优劣的评价函数及后续改进二进制灰狼算法的适应度函数。

2.1 航程代价

航程是评价航迹优劣的重要指标之一。航程代价函数表示为：

式中：Li为航程长度，(xi+1,yi+1,zi+1)和(xi,yi,zi)为对应相邻航点的坐标。

2.2 威胁代价

避障是飞行器飞行任务中极其重要的一个环节，因此本文加入了威胁代价作为评价指标。为简化规划问题，本文在栅格规划环境中，将威胁区及其领空都设为禁飞区，而威胁较小的地形模型允许飞行器通过，于是通过路径线段与威胁源的距离来确定威胁代价，设(xoj,yoj,0)为第j个禁飞区的坐标，roj为第j个禁飞区的边长，则威胁代价函数为：

式中：Sr为飞行器与禁飞区的最小欧氏距离，

2.3 转弯角代价

考虑到飞行器存在机动过载约束和航迹倾角/偏角约束等，航迹倾角、偏角约束限制了飞行器的飞行轨迹弯曲程度，使得转弯角度不易过小，本文加入了转弯角代价函数：

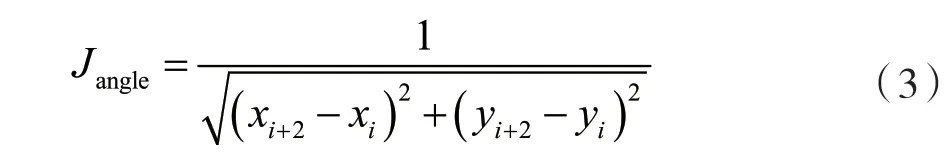
式中：(xi+1,yi+1)，(xi+2,yi+2)以及(xi,yi)对应于相邻航点的坐标，根据三角形特性，(xi+2,yi+2)与(xi,yi)连线越长，转弯角度越大。

综上，总的评价函数为：

3 规划算法

3.1 A*算法存在的缺陷及改进

在边长为l的栅格环境下，A*算法节点扩展时仅可以向与当前节点相邻的8 个方向扩展，步长限制为l，，导致规划得到局部航迹时存在无效转折，如图1 所示，最终导致规划结果并非最短路径。

图1 A*算法局部路径

将A*算法与二进制灰狼算法融合，目的是利用二进制灰狼算法对航迹点进行筛选，直接删除会带来无效转折的节点。

3.2 改进A*算法

A*算法作为一种经典的启发式搜索算法，是静态环境中求解最短路径较为有效的直接搜索方法[7]。针对飞行器航迹规划的问题，本文对A*算法的评价函数[10]做了一定的改变，因为A*算法的主要目的是找寻可行的安全航迹。为保证算法效率，此时仅先将对威胁代价的评价指标考虑到A*算法中，A*的评价函数可变为：

式中：f(n)为当前节点n的评价函数，h(n)为当前节点n到目标点的估计代价。

然而，此阶段A*算法得到的是可行解而不是最优解，因为A*算法过程中，节点扩展只限于栅格线的交叉点，所以得到的航迹点集合存在一部分会使飞行器频繁转弯的节点。而二进制灰狼算法是灰狼算法在特征选择问题上的优化，于是选择二进制灰狼算法对A*算法进行改进。二进制灰狼算法更新过程中，同时将评价函数更新为：

3.3 二进制灰狼算法更新过程

狼群的初始化及更新过程采用二进制灰狼算法[5]进行。为了加快迭代速度，且降低过快陷入局部最优的概率，将头狼简化为一只进行狼群更新[11]。为了使灰狼位置二值化，需要将灰狼的位置转换为二进制矢量来进行位置更新，其公式如下：

式中：r0是[0，1]的随机数，A为系数向量，n是搜索空间的维数，Xα，Xβ，Xδ代表α，β，δ狼在搜索空间中的位置；X1，X2，X3分别定义为受α，β，δ狼影响的二进制步长；X n(t+1)是迭代t时维数n中更新的二进制位置。S(a)定义为：

3.4 算法流程

首先，使用A*算法从起点出发，将以起点为中心的相邻节点中不经过威胁区的节点组成OPEN表，取评价函数值最小的节点放入CLOSE 表中，再以此节点为中心，选评价函数值最小的节点放入CLOSE 表中，从而迅速搜索到一条从起点到目标点评价函数相对最优的航迹，CLOSE 表中的节点即为可行航迹的航迹点。其次，本文将A*算法求取的航迹点集合作为二进制灰狼算法的输入，随机初始化狼群（置0 或1）。再次，对每个航迹点都进行评估，将综合评价函数作为适应度值来评估航迹点集合得到的航迹的航程长短、是否成功避障以及转弯角大小，代价函数越小、适应度越高，得到的航迹越优。根据计算得到的适应度值，选择适应度值最大的3 头狼作为领导者。对于每一只狼，分别使用式（8）计算Y1，Y2，Y3。通过式（9）来更新灰狼位置。再对灰狼的适应度值进行计算，并更新α，β，δ三头灰狼的位置。重复该算法，直到满足终止条件。算法的流程如图2 所示。

图2 算法流程图

4 仿真分析

为评估A*-BGWO 算法的性能，设计了不同规划空间的两个仿真案例进行展示，仿真程序于Matlab 软件中编写。两个案例中，均设栅格单位为km。因为避障在飞行器飞行任务中最为重要，其次是航程长短和转弯角度，所以本文仿真过程中设ω1=0.3，ω2=0.5，ω3=0.2 分别为航程代价函数、威胁代价函数及转弯角代价函数的权重。飞行任务为起点位置到达终点位置并避开威胁区，最小飞行高度设为安全海拔15 km，高于安全海拔的模型即为威胁模型，低于安全海拔的为地形模型。规划出的路径都需要遇到属于禁飞区的威胁模型，飞行器必须从旁侧绕过。遇到威胁较小的地形模型，飞行器可以从其上方飞过。仿真案例的初始参数如表1 所示。

表1 航迹仿真参数

在案例1 中，环境模型随机生成多个不规则地形模型以模拟飞行环境，其中包括高度设置高于安全海拔高度的威胁模型（浅色模型块）和高度设置低于安全海拔高度的地形模型（深色模型块）。图3 展示了A*算法和A*-BGWO 算法的仿真结果及差异对比，其中，白色为传统A*算法规划的航迹，红色为A*-BGWO 算法规划的航迹。改进算法迭代7 次后适应度最优。

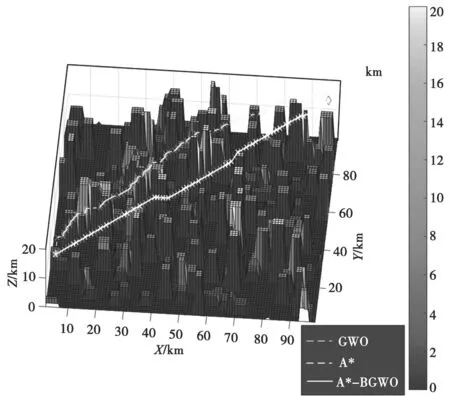
图3 案例1 三维规划航迹

从图3 整体可以看出，GWO 算法转向灵活但搜索航迹较长，规划效果明显次于A*算法和A*-BGWO 算法。

GWO 算法与另两种算法得到的航迹差异较大，暂不做局部对比。因为A*算法与改进算法重合部分较多，所以用图4 展示飞行器避障规划时A*算法与A*-BGWO 算法的局部航迹差异。本文提出的A*-BGWO 算法所规划出的航迹减少了一部分不必要的航迹点（黑点表示），避免了无效转折，航迹转折线路也不受A*算法节点扩展方向限制，因而缩短了航程，规划出的航迹的转弯角度也优于A*算法。

图4 案例1 三维规划局部航迹

案例2 主要展现A*算法和A*-BGWO 算法在威胁区固定的地图模型上的避障效果差异。案例中减少了地图模型上的总威胁源个数，把威胁模型设为规则图形，并把威胁区设置到从起始点到目标点的直线路径附近。威胁区个数在一定范围内对规划结果影响不大，为了显示方便及对比清晰，此案例中将威胁源设置为7 个。图5 展示了A*算法和A*-BGWO 算法的仿真结果及差异对比。

图5 案例2 二维规划航迹

不同规划算法航迹仿真结果如表2 所示。可以看出，A*-BGWO 算法在不影响避障效果的同时，能缩减大部分航迹点，缩短航程。从表2 还可以看出，从起始点到目标点规划航迹上经过的威胁模型数目对A*算法的规划时间的影响较大，而A*-BGWO 算法的规划时间对经过的威胁模型数目增减不敏感，且不会因为地图复杂而严重影响规划效率，运算稳定性更优。

表2 不同规划算法航迹仿真结果

综合以上结果，A*-BGWO 算法的规划时间虽然略高于A*算法，但是搜索效果更好，规划出的航迹总航程更短，优化了转弯角度，故算法具有更好的性能。

5 结语

针对带有多威胁区域复杂地形的飞行器航迹规划问题，本文提出了一种基于改进A*算法的航迹规划方法。该算法利用了A*算法在离散化的地图上求取的结果与二进制灰狼优化算法进行融合，既打破了A*算法节点扩展时带来的转弯角度限制，也使二进制灰狼算法有一个较优的初始矩阵，避免了盲目搜索，能更快得到最优的航迹点集合。随后通过将灰狼的位置转换为二进制矢量来进行位置更新，得到最优航迹点集合，极大地提升了种群的收敛效果。仿真结果表明，该算法能够实时为飞行器规划出一条最短飞行路径，且能有效地避开威胁区域，同时转弯角度更优。