适用于全流型域全倾角范围的井筒漂移流关系

娄文强，王志远,2，李鹏飞，孙小辉，孙宝江，LIU Yaxin，孙大林

（1.中国石油大学（华东）石油工程学院，山东青岛 266580；2.中国石油大学（华东）非常规油气开发教育部重点实验室，山东青岛 266580；3.塔尔萨大学石油工程学院，塔尔萨 74104，美国）

0 引言

随着油气资源需求的不断增长，油气勘探与开发逐渐向深层、深水/超深水、非常规页岩油气资源领域拓展，钻井工况逐渐变得复杂：井下高温高压、储集层类型多变、压力窗口窄、井型复杂[1-2]。多重因素交互影响下的钻完井井筒压力控制难度增加，漏涌事故风险增加，压井关键参数设计难度高。精确计算井筒压力才能精准控制复杂工况下的井筒压力，因此，对井筒多相流动模型的准确性要求更高。深入揭示井筒内多相流动规律，开发具有高适应性的井筒瞬态多相流动模型，对井喷过程分析、压井方案制定、井筒压力的精细控制具有重要意义[3]。

国内外针对井筒内多相流动模拟提出了多种理论模型，漂移流模型因数学形式简单清晰，具有较好的计算效果而被广泛应用[4-5]。简洁的控制方程对相间相对运动的本构方程有较强的敏感性，对其求解要求漂移流闭合关系具有良好的连续性和数学稳定性。井筒漂移流模型的预测精度主要取决于闭合关系（本文中的闭合关系均指漂移流闭合关系），目前漂移流模型的闭合关系分为3种：①基于流型特征开发的闭合关系；②引入平滑函数或加权函数的分流型漂移流闭合关系；③全流型域的单一漂移流闭合关系。

对于基于流型特征开发的闭合关系，气体的漂移速度和分布系数由各流型的漂移流关系确定[6-8]。该类模型对不同流型的预测精度高，但流型转化边界处不连续导致瞬态模拟时多相流动算法收敛困难。利用平滑函数或加权函数处理后，解决了闭合关系的连续性问题，但流型转化边界处计算参数分辨率低，降低了数值计算精度。另外不同管道尺寸、流体类型、管道倾角对流型特征产生了不可忽视的影响，因此依赖流型特征的模型难以描述流动条件多变的流动特征。为了提高漂移流模型数值计算的稳定性，分流型的漂移流闭合关系逐步发展为全流型域的单一漂移流关系。全流型域闭合关系由早期的流型特征组合方式发展为“理论分析+数值拟合”的方式[9-13]，漂移流闭合关系包含的多相流动信息也逐步增加，保证了模型中的多相流动更加真实。该类模型大多基于有限的实验条件或有限的实验数据开发[12]，对实验数据信息存在较强的依赖性。

在井型结构复杂化、压井方案多元化的大趋势下，涵盖全流型域流动特征且具有较高数学连续性的漂移流闭合关系成为精细控制井筒压力的关键[14-15]。本文针对漂移流模型稳定性和适应性问题，构建了多相流动实验数据库，采用理论分析和数据驱动的方式建立了管道倾角为-90°～90°条件下具有强适应性的分布系数和气体漂移速度模型。基于数据库、现场压井案例对该模型进行了综合评价，研究成果可为复杂工况条件下的井筒压力精细控制、生产方案调整提供理论支撑。

1 漂移流闭合关系

1.1 多相流实验数据库

构建了一个包括32个不同数据源共3 561组气液两相流实验数据的数据库，数据库的具体信息如表 1所示。该数据库中实验流体类型有空气-水、空气-煤油、空气-油、氮气-聚维酮溶液等体系，实验液相黏度为0.001～6.880 Pa·s，钻井、压井、生产过程中流体黏度变化范围大，因此包含低黏度到高黏度流体的实验数据对揭示现场流动规律具有重要意义。实验管道的倾角为-90°～90°，涵盖气液同向流动到气液逆向流动的流动类型；管道水力直径为0.012 7～0.152 4 m，覆盖了大范围的流动空间；实验流型包括气液同向、逆向流动的泡状流、段塞流、搅动流、环雾流，涵盖了油气井生产过程、钻井井喷、压井过程中的所有流型。

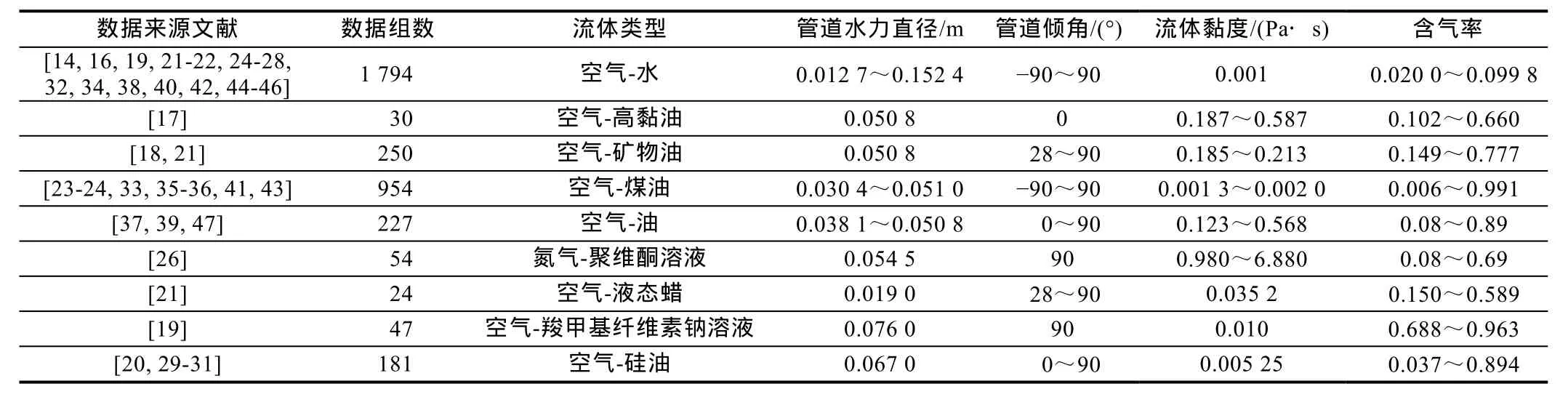
表1 所建数据库实验数据基本信息[16-47]

图 1所示为数据库中各参数数据的分布情况，由图中实验数据点的概率分布情况可知，气相表观速度为0～82.5 m/s，大量实验数据点分布在0～22.5 m/s；液相表观速度为 0～7.25 m/s，大量数据点分布在0～4.25 m；含气率数据在不同管径、倾角、黏度条件下由低到高分布均匀，跨越了两相流中所有的流型，能够表征不同因素对气液两相分布规律的影响；液相黏度为0.001～6.800 Pa·s，主要集中在 0.001～2.400 Pa·s。以往研究中，逆流流动规律的相关研究较少，本文数据库包含了气液同向流动和气液逆流的情况。统计结果表明，该数据库的两相流动数据在各影响因素下分布相对均匀，能够体现各因素的影响规律。

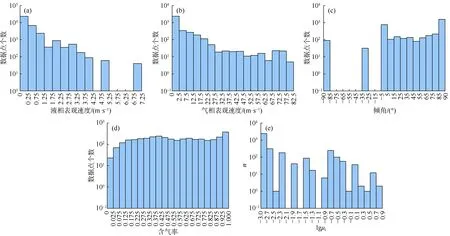
图1 所建数据库中数据分布

1.2 漂移流闭合关系关键参数

漂移流模型的最初概念由 Zuber等[48]提出，描述了气体流动与气液混合流动的相对滑移，揭示了两相流动中气液相之间的滑动差异及气液两相在管道中的分布规律。漂移流模型中的含气率及气体漂移速度如（1）式和（2）式所示：

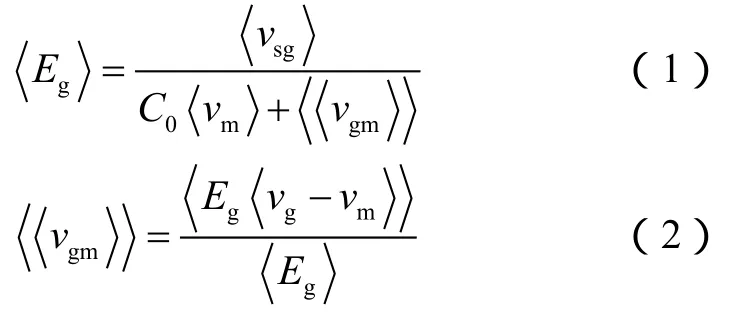
漂移流模型中利用分布系数 C0和气体漂移速度vgm的相关关系计算管道中的两相流动基本参数Eg。由于这两个参数未知，需要采用数学方法进行描述，建立分布系数和气体漂移速度的模型之前需要确定其关键影响参数。

表2所示为基于含气率的部分代表性漂移流模型，前 3个模型代表基于流型特征开发的闭合关系，分布系数为常数，或为与流型相关的系数（为各相密度和含气率的函数）；气体漂移速度是表面张力、各相密度、管径和倾角的函数。Liu等[12]模型和 Choi等[10]模型代表全流型的漂移流关系，分布系数是含气率、雷诺数和各相密度的函数，气体漂移速度是水力直径、表面张力、倾角、含气率的函数。Tang等[13]模型和 Shi等[9]模型代表平滑函数或加权函数类分流型漂移流关系，线性化处理间断边界的一类模型，其分布系数是含气率、各相密度的函数，气体漂移速度是含气率、各相密度、水力直径、倾角、界面张力的函数。除上述参数外，Bhagwat等[11]在研究沸腾（C0＜1）和非沸腾（C0≥1）条件下两相流动气液分布规律时，还引入了气体体积流量分数、两相质量分数和两相摩擦系数，但由于气体体积流量分数和两相摩擦系数难以直接获取，降低了迭代计算效率与模型精度。随着漂移流模型的发展，Wang等[14]认为丰富的两相参数能够更真实地反应两相流动规律。基于已开发模型的物理结构及两相流动规律分析，在保证更全面涵盖物理参数和降低模型复杂性的前提下，分布系数和气体漂移速度可由（3）式和（4）式表示：

表2 漂移流关系相关模型

1.3 漂移流闭合关系构建

1.3.1 气体漂移速度模型

1.3.1.1 管道倾角的影响

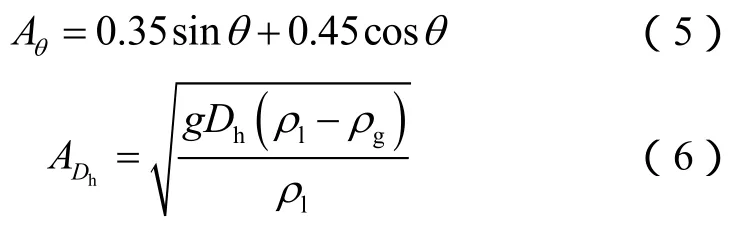
（5）式中Aθ针对管道倾角0°～90°建立，无法解决全倾角范围内的两相流动问题。当管道由水平转到倾斜向下的位置，气体流量较低时，由于浮力作用气相尾部变尖，倾向于向两相流流动方向相反的方向移动。Bendiksen[50]在实验中发现，倾角为-30°≤θ＜0°情况下，当气液混合流体速度小于临界速度时，气体漂移速度出现负值（即与两相流方向相反）。当气相弗劳德数Fr小于0.1时，气相运移速度小于临界速度；超过临界速度时，管道内含气率较高，气相漂移速度将不受管道方向影响。基于上述分析，Bhagwat等[11]提出了一个正负号反转标准：同时满足倾角为-50°≤θ＜0°且 Fr≤0.1，气体漂移速度由正转负，然而该模型不连续，增加了数值算法的收敛难度。本文采用傅立叶变换的思想构造了同时满足倾角-50°≤θ＜0°和Fr≤0.1的符号反转连续函数；将倾角符号切换函数（（7）式）与弗劳德数切换函数（（8）式）相结合，构造了同时满足上述两个条件的连续函数关系。

1.3.1.2 液相黏度的影响

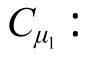
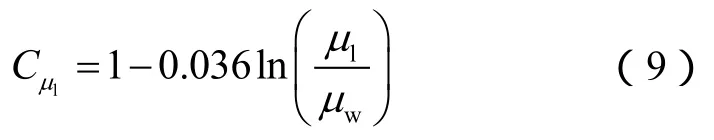
1.3.1.3 气体群间干扰的影响

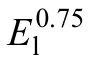
1.3.1.4 管径和表面张力的影响

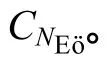
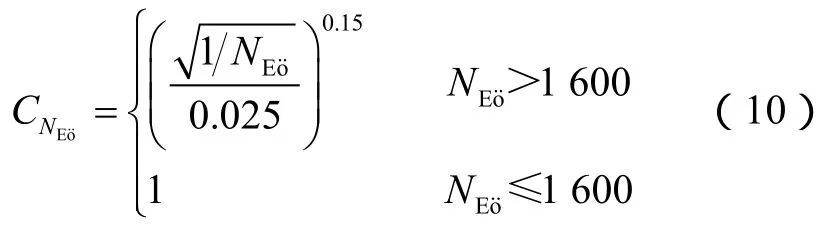
基于以上分析，提出了考虑管道倾角、管径、流体物性参数、含气率的气体漂移速度关系式：

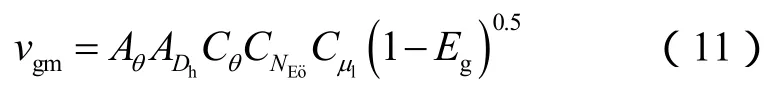
1.3.2 分布系数模型

在确定分布系数与（3）式中流动参数之间的关系前，需要基于数据库实验数据对不同因素的影响进行定量和定性分析。数据统计工作涉及诸多研究学者的实验数据，由于多相流监测技术的进步，实验条件存在显著的差异，这将导致实验数据精准程度不同，相似参数条件下的实验数据存在一定的偏差。采用实验数据库进行定量分析时，需要先对数据进行有效性筛选。

采用前人模型对有效数据进行筛选，首先采用Liu等[12]模型计算所有实验条件下的气体漂移速度和分布系数，筛除分布系数小于 1的数据。然后将筛选出的数据分别采用Choi等[10]模型和Shi等[9]模型计算气体漂移速度和分布系数，依次筛除分布系数小于 1的数据。完成上述操作后，将相同实验条件下明显偏离整体的数据点删除。本文的分布系数模型开发及数据分析均基于筛选后的3 016组实验数据进行。

1.3.2.1 黏度的影响

通过对比表 2中理论模型预测结果与数据库中的数据发现，模型预测分布系数为1.0～1.2，仅符合低黏条件下泡状流过渡到环雾流时的分布系数范围，低估了高黏条件下的分布系数范围（1.0～2.0）。若要提高分布系数关系式在更大黏度范围内（低黏—高黏）的适用性，需要深入挖掘黏度对分布系数的影响规律。黏度的直观影响通过雷诺数体现（Rem=ρlvmDh/μl），分布系数随雷诺数的变化规律如图2a所示，流体黏度增加，流体的扰动降低，气泡受侧向升力的作用更趋向于向管道中心运动，且管道中心处的气泡上升速度最高。分布系数表征气泡在管道截面上分布不均匀性和速度不均匀性，管道中心的气泡聚集程度越高，分布系数越大，因此低雷诺数条件下分布系数较高（超过2.0），超过常规低黏流体中的1.2。高雷诺数条件下，流体湍流效应强，气泡的运移受湍流涡旋的影响，在管道截面上的位置分布具有随机性，分布更加均匀，分布系数趋向于1。综上，流体黏度对分布系数的影响主要体现在气液两相流动的湍流程度，采用雷诺数解释分布系数的变化规律如下式[12]，其中第1项代表低雷诺数项，第2项代表高雷诺数项：

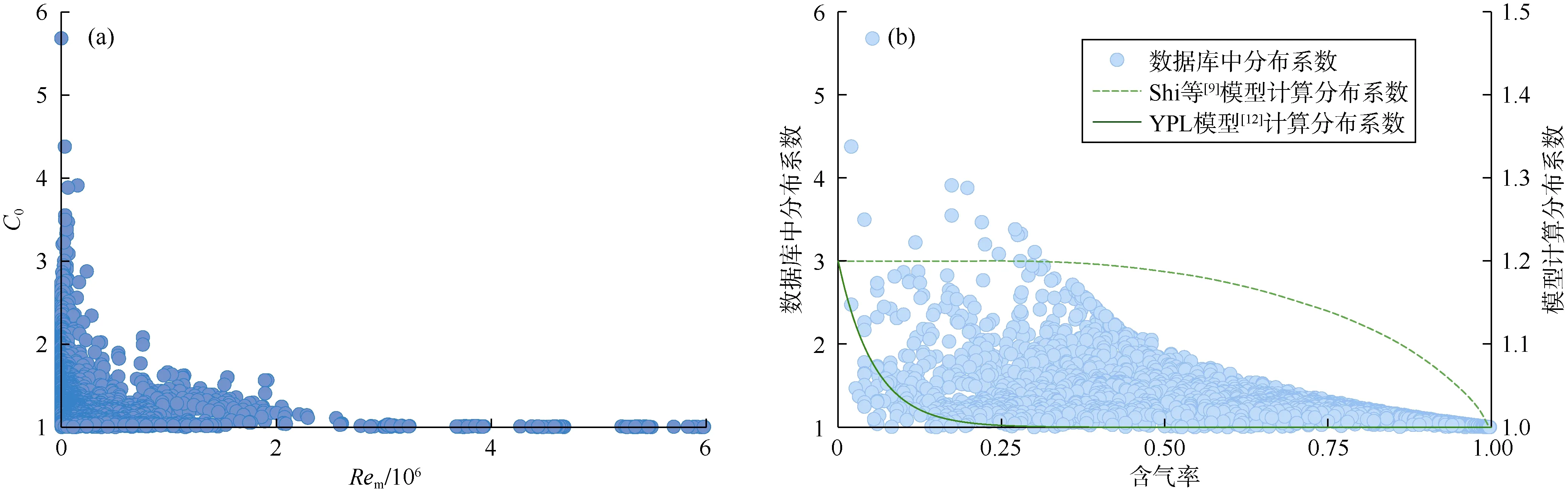
图2 分布系数相关性分析

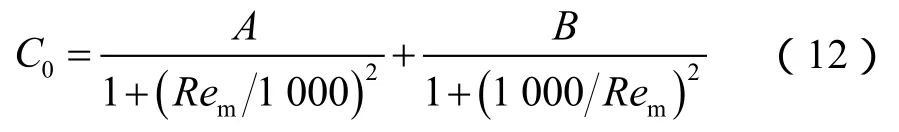
1.3.2.2 管道倾角的影响

管道倾角影响两相流体的重力体系，气体在管道中的分布随倾角发生改变。在管道内流体由垂直向上流动逐渐转变成水平流动的过程中，分布系数呈降低的趋势；当流动方向继续转变为向下时，气体出现两个运移方向，气体分布也随运移方向变化而改变。因此，采用B0表征倾角的影响，如（13）式所示。

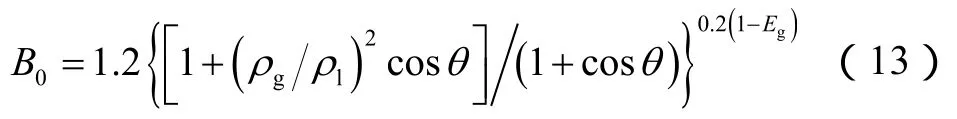
1.3.2.3 含气率的影响

两相流动中气相分布情况与管道中的流型密切相关，含气率作为流型表征最关键的参数，与分布系数强相关。图2b显示了数据库中分布系数与含气率的相关性，以及 Shi等[9]模型和 YPL（Yield-Power-Law）模型[12]预测的分布系数随含气率的变化趋势。Shi等[9]模型预测的分布系数与含气率的相关性表现出凸函数性质，与实验数据变化规律不吻合；YPL模型虽然低估了分布系数，但能反映出分布系数随含气率的变化趋势，对全流型域内分布系数的描述优于 Shi等[9]模型。因此，采用YPL形式（14）式能够相对准确地描述全流型域内分布系数的演化规律。

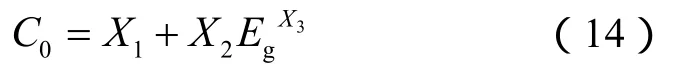
综合考虑上述因素，流体黏度影响下的分布系数方程由低雷诺数项和高雷诺数项构成，分布系数与含气率的相关性采用YPL形式，同时将管道倾角的影响关系式作为新的屈服项替换YPL形式中的X1项，构造出新的分布系数方程：

利用多相流动实验数据库中的数据对（15）式进行参数化分析，以计算含气率与实际含气率的平均误差最小化作为目标进行优化，最终得到常系数A、X1、X3分别为 2.0，-0.2，6.8。

1.3.3 模型性能

（15）式综合考虑了含气率、管道倾角、流体物性参数的影响，覆盖广泛的多相流动工况。本文漂移流模型综合了多参数、多源数据，因此需要对模型的稳定性进行分析，保证模型具有良好的连续性和稳定合理的物理参数预测值。

图 3为垂直管道中不同含气率条件下分布系数随雷诺数的变化规律。在低雷诺数范围内（Rem＜1×102），液体对气体运动轨迹扰动能力弱，气体运动规律受管道内层流流场的影响，管径方向上气体速度分布具有抛物线性质，因此分布系数表现为较高值，受含气率的影响较小。在过渡带（Rem为 1×102～1×104），流体扰动作用影响明显，气体分布系数随雷诺数增加迅速降低。进入高雷诺数区（Rem＞1×104）后，气体受液体扰动作用增强，分布更加均匀，分布系数稳定在较低值。由图可知，含气率对分布系数的影响主要体现在高雷诺数区，随含气率增加，分布系数由 1.2减小到1.0，反映流型变化对分布系数的影响。

图3 含气率对分布系数的影响规律

随井深增加，气相的物性参数发生变化，气体密度增加对气液两相的分布规律产生不可忽视的影响。图 4为不同气液密度比条件下分布系数随雷诺数的变化规律。与含气率相反，密度对分布系数的影响主要集中在低雷诺数范围内。随密度比增加，气相的滑脱效应减弱，气液两相的分布趋向于均匀，因此分布系数降低。在深井、超深井发生溢流时，气体上升过程中的气体漂移速度和分布系数都发生变化，采用常规分布系数模型难以精准预测井筒压力的变化。

图4 密度比对分布系数的影响规律

管道倾角影响气体的漂移速度和分布情况，进而影响含气率，斜井、大位移水平井的井筒压力控制取决于模型敏感性和稳定性。图5a所示为不同倾角下的预测含气率，管径设为0.05 m，液体黏度为0.001 Pa·s，液体的表观速度为0.5 m/s。随倾角绝对值的增加，含气率呈降低趋势，主要是由于重力作用下气体的滑脱效应增强，气体由均匀分布转变为在管道中心集中分布，进而导致分布系数增加，含气率降低[11]。同时，井筒内流体的流变性对气体的漂移规律、流型转化边界都有影响，井筒压力的精准控制需要模型对流体黏度具有较高的敏感度。图5b为垂直管道内不同黏度流体预测含气率随气体表观速度的变化，管径为0.05 m，液体表观速度为0.5 m/s。流体黏度增加，气液混相流体雷诺数显著降低，分布系数随之增加，含气率随之减小。

图5 管道倾角和流体黏度对预测含气率的影响规律

2 模型验证及应用

2.1 漂移流模型验证

利用本文建立的多相流动实验数据库，对本文提出的漂移流关系及 Liu等[12]、Choi等[10]、Hibiki等[8]提出的漂移流关系进行了预测评价，模型预测结果如图6和表3所示。不同模型对环雾流数据的预测效果最好，数据点集中分布在±20%的误差范围内，其中本文模型和Hibiki等[8]模型的预测结果主要集中于±10%的误差范围内，Choi等[10]模型预测效果差的原因是环雾流条件下分布系数预测值偏高，影响含气率的计算。所有模型对泡状流和段塞流的预测都存在异常离散点，本文模型、Liu等[12]模型、Choi等[10]模型采用相同的构造形式，对泡状流和段塞流的预测值偏高点居多，主要原因是在雷诺数较低的情况下对分布系数的估计值偏低；而 Hibiki等[8]的漂移流关系基于流型建立，在不同流型内具有不同的偏离程度。为了对漂移流关系的预测效果进行定量分析，采用平均残差 ε1、平均相对误差ε2和标准差ε3对模型计算结果进行统计分析。

图6 不同模型含气率预测值与实测值的对比

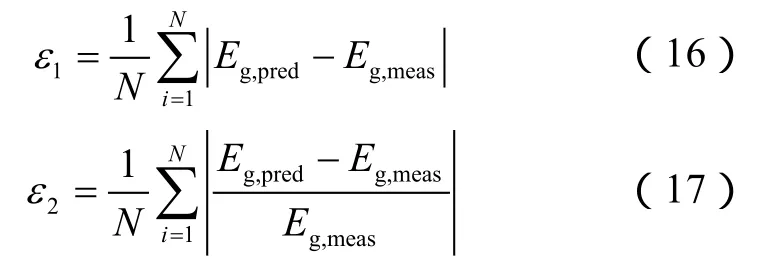
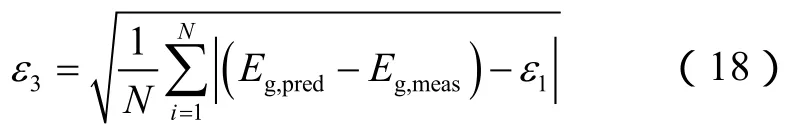
表 3所示为不同模型预测效果的定量评价结果，本文模型与 Choi等[10]模型预测结果在±20%误差范围内的数据点占比达到80%，Liu等[12]模型与Hibiki等[8]模型预测结果在±20%误差范围内的数据点占比分别为76.36%和75.56%。Choi等[10]模型预测结果在±10%误差范围内的数据点明显减少，这主要是由于环雾流的预测误差导致；Liu等[12]模型和Hibiki等[8]模型在该误差限内的预测精度相当，本文模型在该误差限内的预测数据点占比明显高于其他模型。统计结果显示，本文提出的漂移流关系预测值与数据库中的实验测量值的平均残差最小，最接近于实验测量值。预测误差的标准差揭示了预测误差的分布均匀性，本文模型在保证残差最小的基础上同时具有最低的标准差，保证了模型预测的稳定性。统计分析结果显示本文模型在该实验数据库条件下的预测效果最优，具有良好的漂移流计算精度和预测适应性。

表3 不同漂移流关系预测结果

2.2 漂移流关系在井筒多相流中的应用

2.2.1 非稳态漂移流模型求解

影响井筒漂移流模型预测精度的另一个因素是非线性方程组的数值求解格式。有限体积法通过积分的方式处理多相流动方程，在物理守恒性、计算稳定性、鲁棒性方面优于有限差分法，近年在计算流体力学和流体工程领域广泛应用。本文采用交错网格的有限体积法处理多相流动方程组的空间对流项，选择一阶迎风格式离散多相流控制方程的对流项，选用一阶向后差分格式离散控制方程的非稳态项。借鉴 Wang等[14]对界面参数的处理方法，依托类SIMPLE（Semi-Implicit Method for Pressure Linked Equation）方法搭建多相流动方程的压力预报-校正求解框架，耦合Liao等[15]提出的井筒温度场算法，实现井筒非稳态多相流动模拟。

2.2.2 压回法压井模拟

本文建立的漂移流模型涵盖了倾角为-90°～90°的流动情况，对不同工况下的压井模拟具有一定的指导意义。为验证本文建立的井筒漂移流模型的适应性，针对塔里木油田某井压回法压井过程（管道倾角为-90°～80°）进行了模拟，该井的相关参数如表4所示。

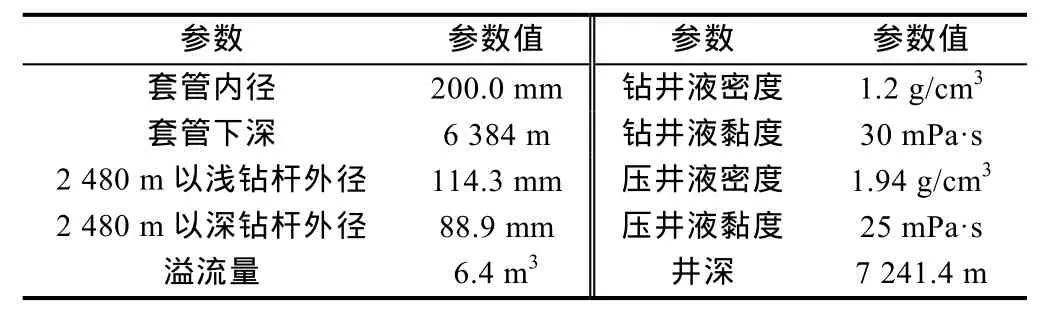
表4 塔里木某井相关参数

该井储集层段为受断裂控制的碳酸盐岩缝洞型储集层，钻进过程中突发溢流，关井完成时钻井液池增量6.4 m3，关井后井口压力41.8 MPa。受气体组分影响采用环空注液压回的压井策略，为保证井口安全性，先用20 L/s排量压回，后增加排量至24 L/s。采用本文模型对整个压井过程进行了模拟，模拟结果如图 7所示。关井至24 min时井口套压为42.88 MPa，此时采用20 L/s的排量由环空注入1.94 g/cm3的高密度压井液，井口套压迅速增加至54.24 MPa，压井液进入后井口回压逐渐降低。40 min时压井排量增加至24 L/s，井口套压突增为47.30 MPa，随压井液驱替及气体压回地层，井口套压逐渐降低。压井液到达井底后，完成压回法压井，此时井口回压稳定在2.61 MPa。由图可知，模型计算结果与现场数据高度吻合，关井套压计算误差为2.58%，初始压回套压计算误差为3.43%，调整排量时的套压计算误差为5.35%。

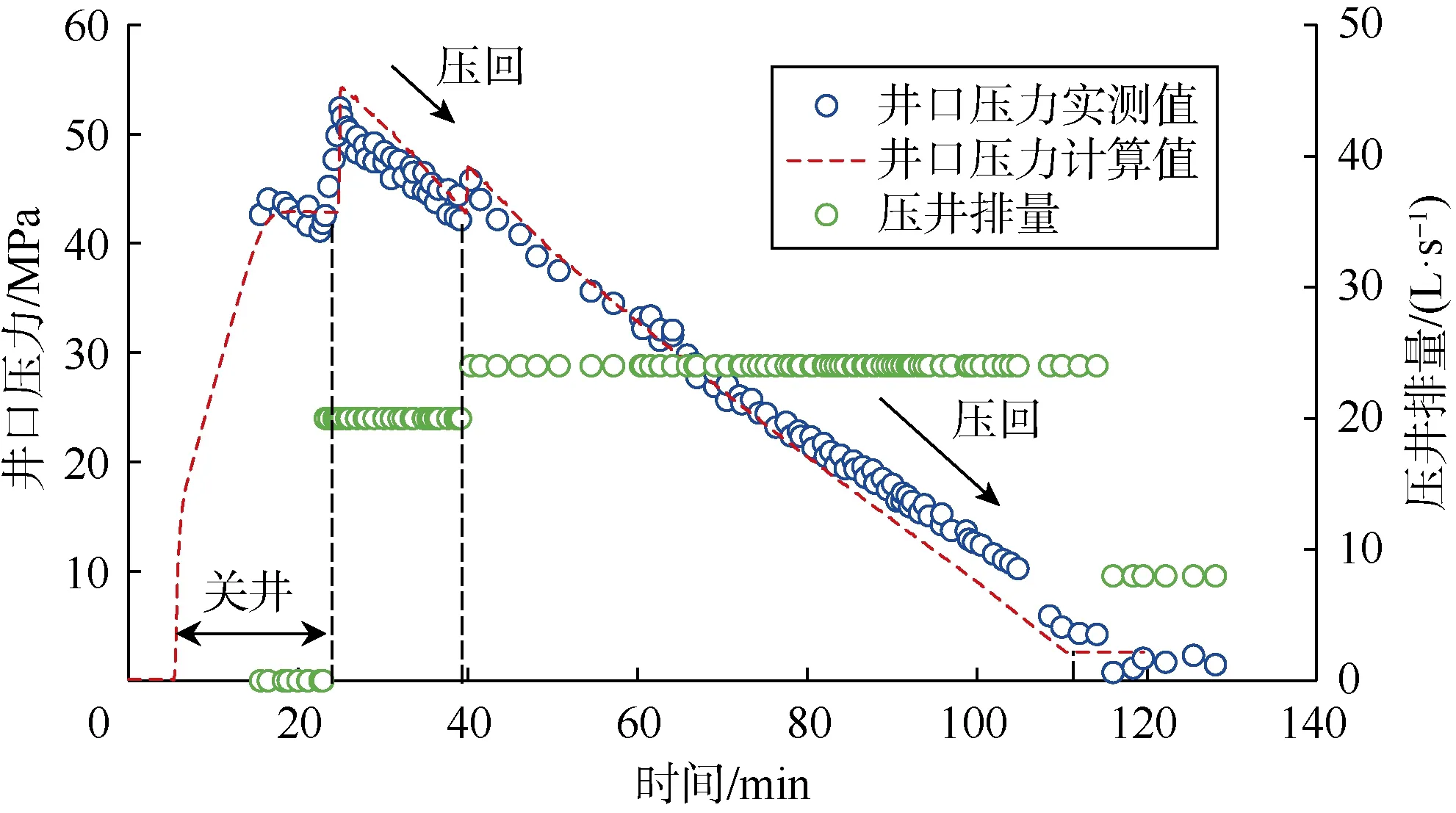
图7 压回法压井过程中井口压力变化

图 8为压回过程中不同时刻井筒含气率的变化，24 min为压回法压井的初始时刻，由于井筒续流作用，含气率表现为高值，井筒内出现段塞流，压回排量需要将段塞流中的 Taylor泡压回。Taylor泡的上升速度比泡状流中的小气泡上升速度高[54-55]，因此需要较高的压回排量才能将气体压回地层中。由于气体的上升过程被抑制，气体逐渐被压回到地层中，气体的运移速度远小于压井液的下行速度，压回效率低。因此，40 min后提高排量，高含气率气包被快速压回。由50～80 min的压回过程可知，随着井筒内含气率降低，气体下行速度增加，压回速率逐步提高。当压井超过110 min后，井口回压稳定，井筒内气体被全部压回地层。

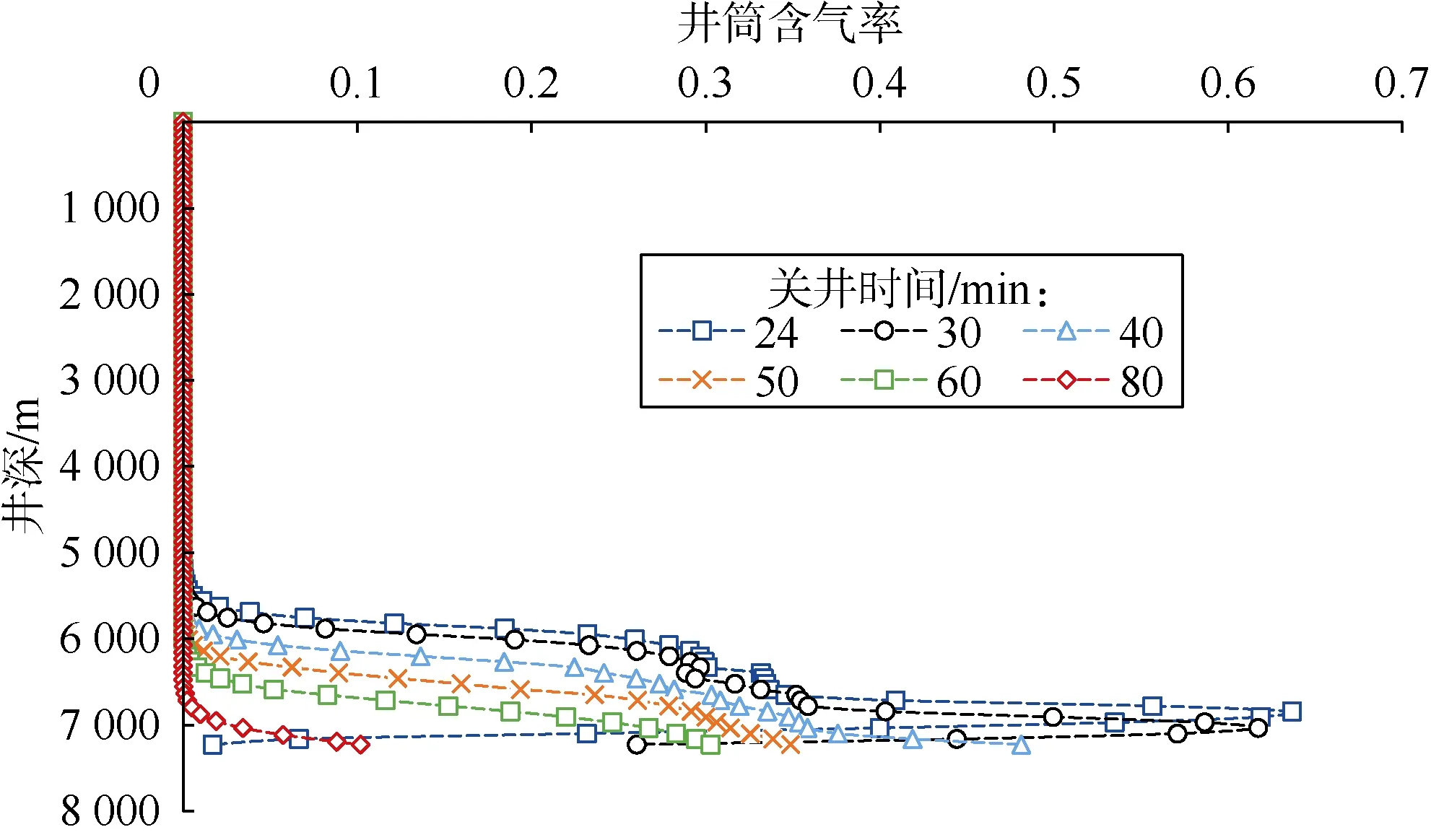
图8 压回过程中不同时刻井筒含气率的变化

3 结论

井筒多相流动中，气体漂移速度主要受管道倾角、管径、流体物性参数、含气率的影响，分布系数主要受流体黏度、管道倾角、含气率的影响。本文基于理论分析和数据驱动方式构建的全流型域全倾角气液两相漂移流关系模型具有良好的连续性和稳定合理的物理参数预测值。模型计算结果与数据库中的数据对比发现，本文模型在±20%和±10%误差限范围内的预测数据量占比分别为80.86%和62.63%，预测误差的标准差为0.065 2，与现有模型相比预测精度最佳，预测稳定性最高。针对管道倾角为-90°～80°的流动工况，关井套压模拟误差为 2.58%，初始压回套压模拟误差为3.43%，调整排量时的套压预测误差为5.35%，逆向流动条件下模型的计算结果与现场具有较高的吻合度。

本文的漂移流关系解决了分流型模型在模拟非稳态多相流时计算难以收敛和计算效率低的难题，在复杂流动条件下具有较高的稳定性，对井筒压力精细控制、安全生产作业具有重要的指导意义。

符号注释：