基于新型检测方法的带式输送机滚筒故障诊断
2022-07-14张强
张 强
(西山煤电(集团)有限责任公司机电厂, 山西 太原 030053)
引言
在海上运砂机中,滚筒是带式输送机最常用、最易发生故障、维修最频繁的部件[1-2]。滚筒容易堵塞、断裂等,严重影响带式输送机的正常运行。传统的滚筒故障诊断是人工检测,需要定期安排工人对滚筒进行检测[3-4]。人工检测费时费力,不能及时发现故障。近年来,故障诊断方法从传统的人工诊断迅速发展到智能诊断[5]。基于数据的故障诊断基本过程主要包括信号处理、特征提取和故障分类。为了解决滚筒故障的多分类问题,本文提出了一种基于音频小波包分解和CNN 的智能故障诊断方法。与传统的人工检测相比,大幅提高了滚筒的故障诊断效率。
1 带式输送机设备的描述
1.1 结构组成
带式输送机整体构造主要是由输送带、机架、驱动和托辊组结构组成的,除此之外还需要配套拉紧装置、装载装置和清扫装置等辅助系统。驱动作为整个传输机中的核心部分,为整体提供源动力,驱动系统由减速器、电机和传动滚筒组成。输送带部分由托辊组构成,绕过输送机头的传动滚筒、输送机尾部改变方向的滚筒组合成闭合回路,托辊组能够起到减小输送带摩擦的作用,如图1 所示。
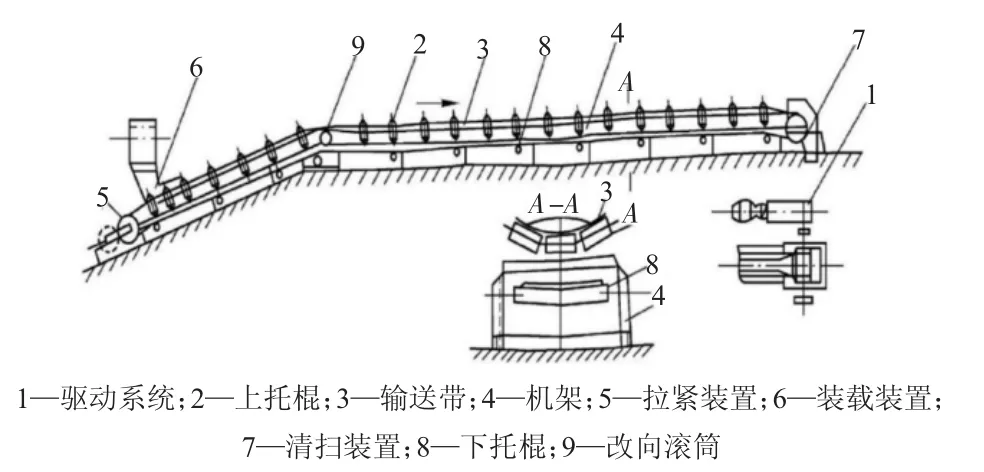
图1 带式输送机结构示意图
1.2 工作原理
带式输送机由电机带动减速器和传统滚筒运转,将需要输送的物料由装载装置从输送机尾部放置在输送带上,输送带通过传动滚筒之间产生的摩擦力将物料输送到输送机头部分并卸下,位于输送机头部分的清扫装置能够将输送带上残留的物料清理干净,残余物料不会对带式输送机的正常运作产生影响。带式输送机在正常运行过程中,输送带需要达到一定的张力,小功率输送机需要用拉紧装置进行张紧,大功率输送机采用重锤张紧。
1.3 带式输送机可靠性分析
建立带式输送机可靠性模型框图,分析输送机各个子系统之间的组成部分,在可靠性分析中,每个子系统的零件可靠度都是相当关键的,任何一个子系统出现故障都会影响到整机系统的性能。分析每个组件在系统中所处的作用,构建组件之间的可靠性关系,获得整体系统的可靠性模型。
可靠性分析过程中,框图要简明扼要,很直观地反映各组件在系统中的作用,找到其薄弱环节,重点对其进行改进,这样带式输送机的可靠性也就能大幅提升,带式输送机可靠性模型搭建如图2 所示。
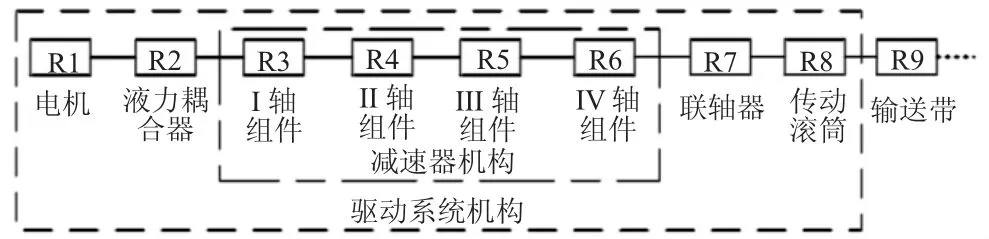
图2 带式输送机可靠性模型
2 基于CNN 的滚筒故障分类算法
2.1 数据特征提取
经过n 层小波变换,得到2n 个频带。本文采用8层小波包变换,对每组数据进行256 个频带数据的处理。256 个频段的数据很难转换成二维数据,并输入到CNN 中。因此,应该计算每个频带的数据特征。滚子数据的特征包括能谱、标准差和平均值等。能谱计算公式为:
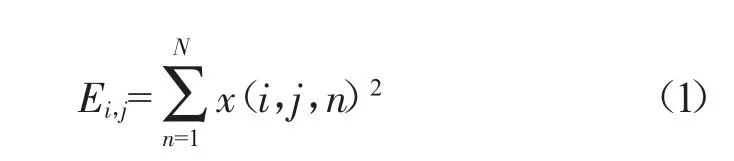
式中:Ei,j为第i 层第j 段频带的能量;x(i,j,n)为第i层第j 段的数据。通过分析各频段的能量占比可知,最低频段的能量占总能量的12%左右,明显高于其他频段的能量占比。
2.2 CNN 分类算法
设备的故障诊断需要对其特征进行分类。由于环境复杂、数据量大以及滚轮噪声大等原因,不能通过简单的逻辑判断对数据特征进行良好的分类。本文使用CNN 对特征进行分类。CNN 是一种包含卷积运算的神经网络,可以同时处理多维输入数据。CNN 作为一种监督分类算法,需要收集滚筒的每个状态的音频数据,然后为每个数据设置标签。除了调整网络结构外,其他方法也可以优化神经网络的性能。CNN 是一种深度神经网络,包括输入层、卷积层、池化层、全连接层和输出层。
对滚筒的音频数据进行8 层小波包变换,得到256 个频带。每组特征包含256 个数据,转换为16×16 个二维数据。对于CNN 来说,16×16 个输入数据很容易处理。本文所使用的CNN 模型是由LeNet-5衍生而来,经过适当的修改,该模型共有5 层。输入数据的大小是16×16,输出数据的大小是3×1。CNN包括两个卷积层、两个池化层和一个输出层。
3 实验验证
3.1 实验介绍
为保证算法的鲁棒性,采集了46 组皮带空载和输送的音频数据。采样频率为44100 Hz,每个音频段大约有20000 个采样点。根据滚筒的运行情况,滚筒分为三种状态:
1)正常状态:滚筒运行正常,无需维护。
2)异常状态:托辊卡死,即托辊与皮带分离。这类故障危害较小,操作完成后即可修复。
3)故障状态:滚筒断裂,该故障可能会导致非常严重的后果,设备需要立即停机检修。
在神经网络中,大量的数据有利于训练。通过细分每组数据,可以获得更多的数据。每组原始数据中约有2 万个数据点。将原来的46 组数据扩大到230组,将4000 个数据点分成一组。本文将滚筒分为三种状态,“100”表示正常状态,“010”表示异常状态,“001”表示故障状态,利用滚轮的音频数据进行实验。
3.2 实验分析
在本实验中,使用200 组数据作为训练数据集,使用30 组数据作为测试数据集。CNN 被用来进行分类,CNN 的结构如图3 所示,均值和标准差作为训练CNN 的特征。通过比较两种特征的分类精度,选择更合适的特征。从图3 可以看出,两种特征的训练误差都很低,误差曲线都很快稳定下来。当特征值为均值时,训练误差为2%,当特征值为标准差时,训练误差为4%。但是,从表1 可以看出,对于测试数据集,均值作为特征的分类准确率为86%,标准差作为特征的分类准确率为93%。因此,采用标准差作为数据特征可以更有效地诊断滚筒故障。
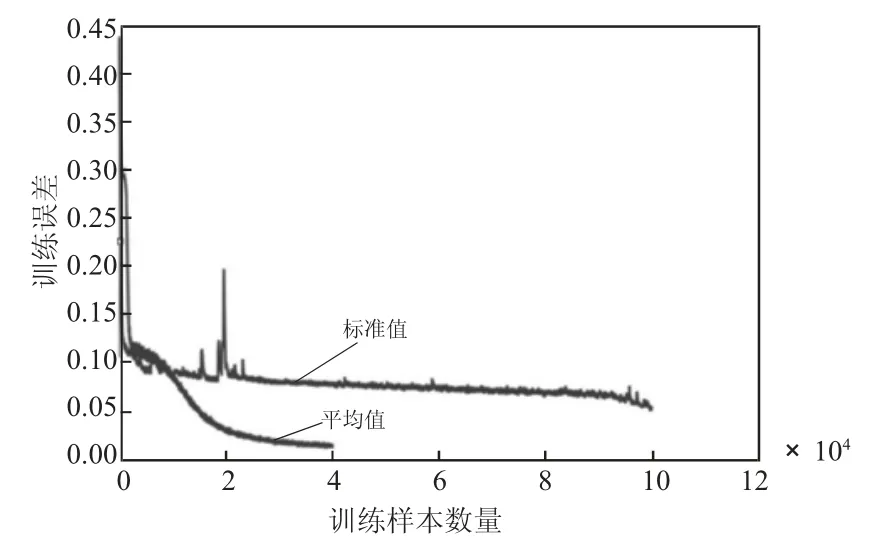
图3 训练误差曲线
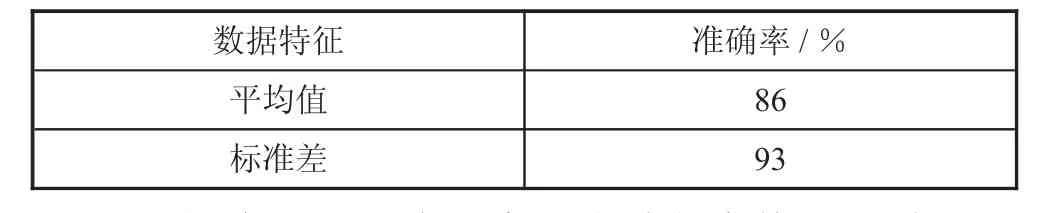
表1 不同特征测试数据集的分类精度
同时,本文进一步研究了小波包变换后通过调整最小频带数据来提高分类效果。以标准差作为数据特征,比较是否调整最低频带数据的分类精度。由表2可知,未调整最低频带数据的测试数据集,分类准确率为90%,调整最低频带数据的分类准确率为93%。因此,通过调整最小频率数据,可以提高轧辊故障诊断的效果。

表2 测试数据集的分类精度
实验表明,本文提出的基于小波包和CNN 的故障诊断方法能够有效地诊断出轧辊的故障,以标准差作为特征可以更准确地进行分类,小波包变换后调整最小频带数据,减少低频数据的影响,可以使分类效果更好。
4 结语
本文利用小波包变换和CNN 对音频信号进行故障诊断。首先,利用小波包变换将音频信号分解为256 个频带,由于最低频带的能量占比过大,因此对最低频带的数据进行调整,以降低其对故障诊断的影响。然后计算标准差和均值作为数据特征。实验结果表明,采用标准差作为数据特征的方法对轧辊故障诊断更为有效。
