基于RBF神经网络的船舶冲击谱速度数据挖掘与预报

2022-07-14冯麟涵杨俊杰焦立启

振动与冲击 2022年13期

冯麟涵，杨俊杰，焦立启

(1. 海军研究院，北京 100161； 2. 大连船舶重工集团有限公司，大连 116000)

随着反舰武器的多样化和更新换代，爆炸的当量、冲击持续的时间都有明显增加，且各种攻击武器的命中率显著提高，使水面船舶面临更为严峻的威胁，而船舶抗爆抗冲击能力更是决定船舶战时生命力强弱的重要因素，直接关乎船舶的生命力与战斗力。水下非接触爆炸产生的冲击波、气泡脉动和滞后流等复杂冲击作用遍及全船，对船舶机械、设备以及系统产生影响，严重影响战斗能力。设备抗冲击性能考察的指标主要有谱加速度、谱速度、谱位移，其中速度谱用于考核不同冲击对结构的破坏潜能，被广泛应用于船舶设备的抗冲击考核[1]。

但设备冲击环境预测快速预测技术尚不成熟。经验理论预报方法预测快速但精度相对较低，有限元仿真预测方法虽然预报精度较好，但需要创建复杂的有限元模型以及花费大量的计算成本，预测速度相对较慢[2-3]。冯麟涵[4]利用PSO神经网络算法建立船舶冲击环境预测模型，对船舶在各种可能攻击情况下的冲击环境进行工程化预报，具有良好的通用性。Gao[5]利用PSO、OLS等算法优化了RBF神经网络结构，将提取的16个声源数据参数作为输入变量对船舶舱室噪声进行了预报。古滨等[6]使用样本库的方法对船舶冲击环境进行预报，比较全面的总结了冲击环境与冲击因子、爆距、船长等之间的关系。但由于上述预报需要大量数值模拟或试验数据，船舶冲击环境预测方面还缺乏合适的智能方法进行相应的数据挖掘研究。本文提出基于径向基神经网络对水面船舶在水下非接触爆炸作用下的冲击环境进行研究与预报。如前所述，对于船舶冲击环境的预报需要大量数据进行训练，故本文利用参数化建模程序，快速建立若干设计合理的船舶模型，并通过仿真方法产生大量格式统一、分布合理的船舶冲击环境数据。分别将船舶的主尺度参数、船舶水下爆炸数值仿真的工况设置参数以及考察点的位置坐标作为神经网络的输入参数，以船舶考察点的谱速度作为输出对搭建的RBF网络进行训练，并通过聚类算法对网络参数进行优化处理，模型训练完成后对未知船舶在给定工况下的冲击环境进行了预报及分析。

1 基于RBF网络的数据挖掘与预报理论基础

1.1 径向基神经网络工作机理

径向基神经网络由Moody和Darken于1988年提出，简称RBF网络，用于函数的精确内插。RBF网络具有唯一最佳逼近、训练简洁、学习收敛速度快等良好性能，并且具有很强的非线性拟合能力，可逼近任意的非线性函数，具有较好的泛化能力，现已成功应用于语音识别、自动控制、信息图像处理和故障诊断等多个领域[7-9]。本文将基于RBF网络进行船舶冲击谱速度数据的挖掘与预报。

RBF网络是一种具有三层神经元的前馈神经网络，分别是输入层、隐含层和输出层，如图1所示。

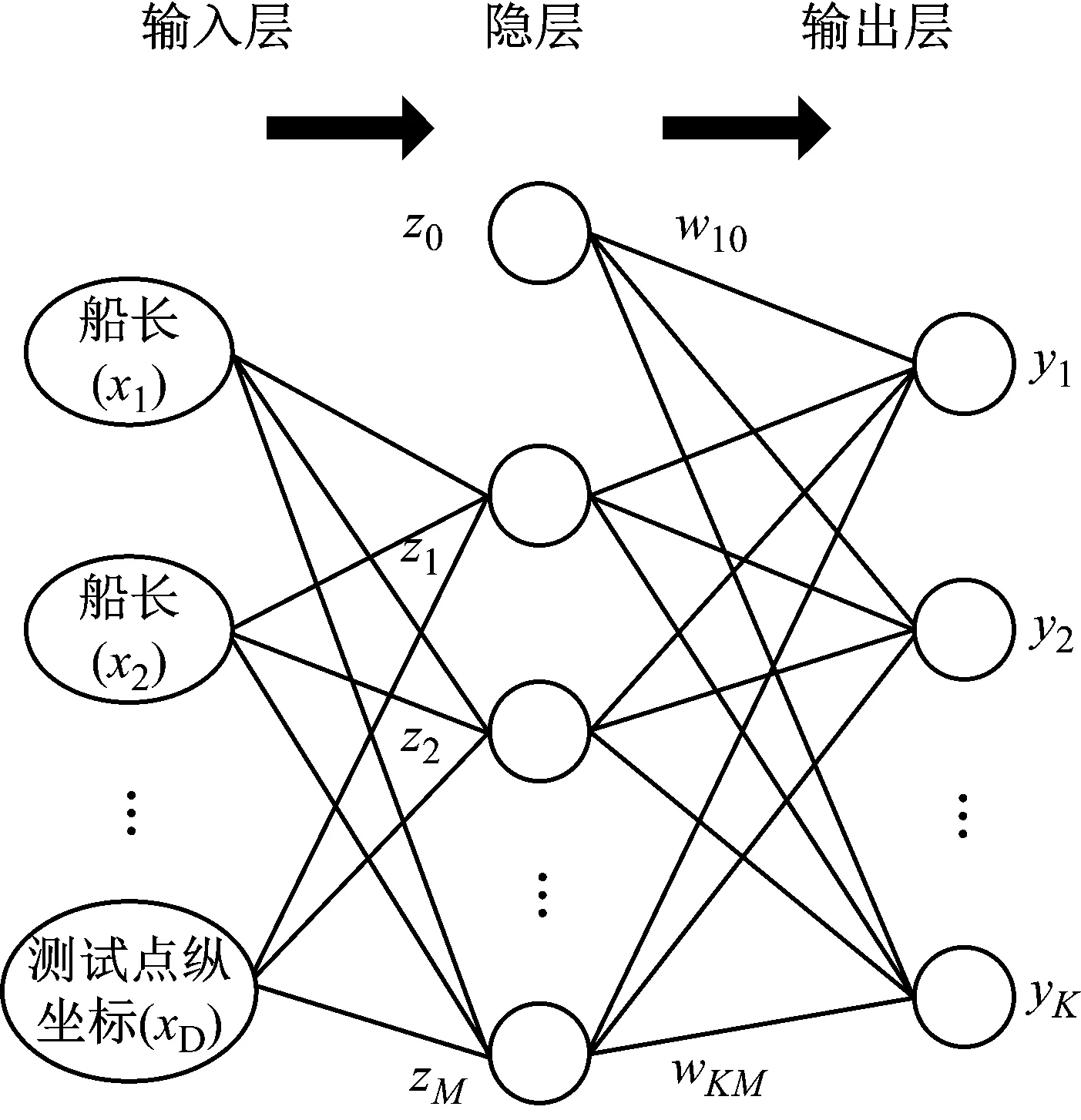
图1 径向基神经网络结构Fig.1 Radial base neural network structure

在图中，输入变量参数由船舶的主尺度参数(包含船长、船宽、吃水和排水量)、船舶水下爆炸数值仿真的工况设置参数(包含爆距、冲击因子、攻角以及药包质量)以及考察点的位置坐标作为神经网络的输入参数。

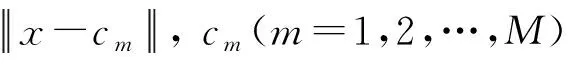
(1)

式中：xn(n=1,2,…,N)为第n个样本；σm为第m个隐节点中心cm的宽度。在不影响普遍性的情况下，以σm=1，根据向量2-范数与欧式距离在表达上的一致性，易证明其输出可以表示无穷多维

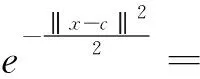
(2)

由上式得到特征映射函数

(3)

式子右边有无穷项，因此径向基函数对应的特征空间是无穷维的。

图1中第k个输出可以表示为

(4)

从式(4)可以看出，每个隐层神经元都会响应输入x，而RBF网络的输出则是这些响应的加权和。输入x离第m个隐节点中心cm近，则响应大，离得远，则响应小。这种特性被称为“局部映射”特性，这一特性使得RBF网络跟“全局映射”的网络相比，收敛速度更快。

1.2 基于聚类算法的RBF网络学习算法

聚类算法属于机器学习领域的非监督学习，通过对无标签的一组数据进行分类的算法，最先由Moody和Darken引入RBF网络[12]，一般用来求隐节点中心的坐标。K均值聚类算法是RBF网络最常用的聚类学习算法。

K均值聚类算法的思想是以空间中K个点为中心进行聚类，对最靠近的对象进行归类处理，再通过迭代逐次更新各聚类中心的值，直至得到最好的聚类结果。所获得的聚类满足：同一聚类中对象的相似度较高，不同聚类中对象的相似度较低，即对样本集{x1,…,xN}，K均值聚类算法将个样本划分到K个集合中K≤N，使得组内平方和最小。

K均值聚类算法流程如图2所示，具体步骤是：

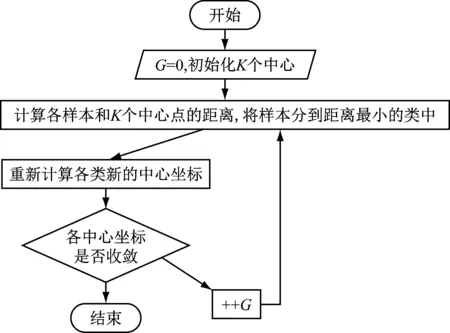
图2 K均值聚类算法流程Fig.2 The algorithmic process of K average clustering

(1) 设置聚类个数K，随机选取K个训练样本点作为隐节点的初始中心，初始化迭代次数G=1；

(2) 在第G次迭代中，求训练集中任意一个样本到K个中心点的距离，得到具有最小距离的样本并将其划分到距离最小的类中；

(3) 利用均值法计算更新G次迭代后的中心点；

(4) 所有的K个中心全部经过步骤(2)和(3)后，各个中心坐标不变或变化小于某个阈值，则迭代结束，否则转至(2)继续迭代。

K均值算法中K的值需要根据经验事先确定，且对聚类中心的初始化要求较高，容易陷入局部最小值。由于算法的运行时间一般较短，可通过设置不同的初始状态运行多次从而得到更好的结果。

各聚类中心确定后，径向基函数的拓展常数σm可由下式决定

(5)

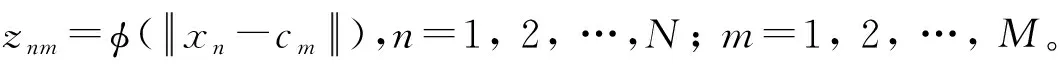
(6)

设输出权值为w=[w1,w2,…,wM]T，则网络输出可表示为

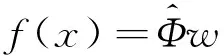
(7)

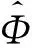
(8)

将式(7)左乘到式(8)等号两边可得

(9)

2 船舶冲击环境训练数据库建模

船舶冲击环境是指水下爆炸载荷作用下船体各部位的基础输入，对于舰载设备而言即是其安装基础处所经受的冲击加速度、冲击速度和位移[13]。数据集一般通过仿真预测获得。以ABAQUS软件计算为例，其开展冲击环境计算时是基于声固耦合法，将流体作为声学媒介，用声学单元来描述流场[14]。在仿真计算中，计算模型主要由骨材、板以及流场实体组成，分别以梁单元、壳单元和四面体单元分别进行有限元划分，其中梁单元与壳单元尺寸一致，本次计算单元大小取为0.5 m，对于四面体流场单元，靠近船体位置的单元大小略小于结构单元尺寸即可，流场外侧单元大小取为贴附船体位置流场单元大小的4倍～6倍。

仿真计算主要包含了10艘不同吨位的船舶，其主尺度参数如表1所示。分别设置工况进行水下爆炸仿真计算，将不同考核点的历史输出进行提取和数据后处理。以10号船舶为例，其有限元计算模型如图3所示[15]，考核点布置如图4所示。

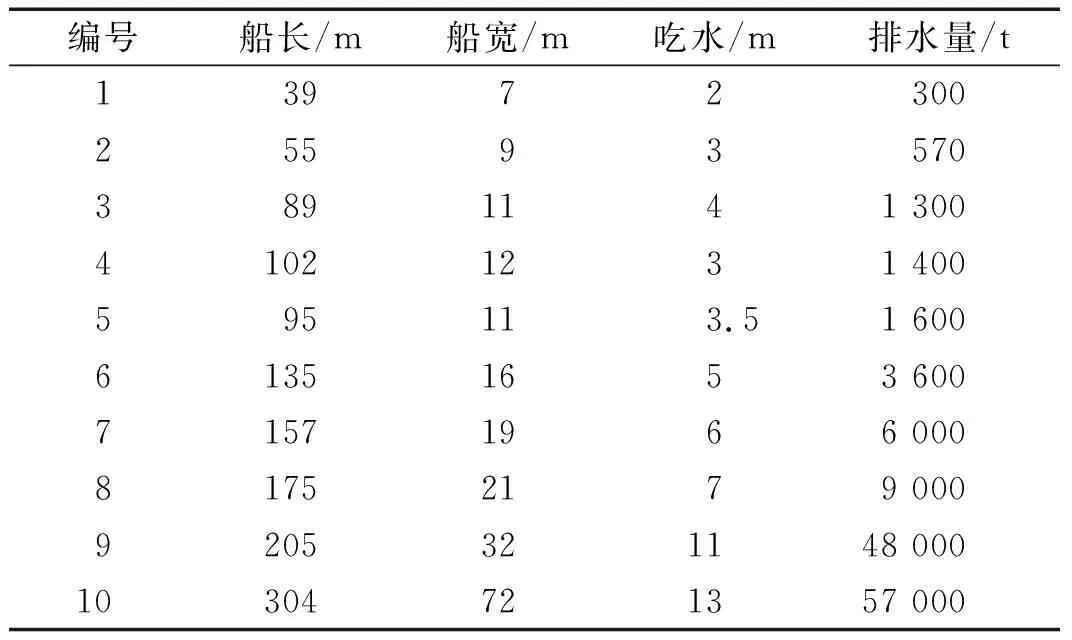
表1 船舶主要尺度参数表Tab.1 Principal dimension parameters

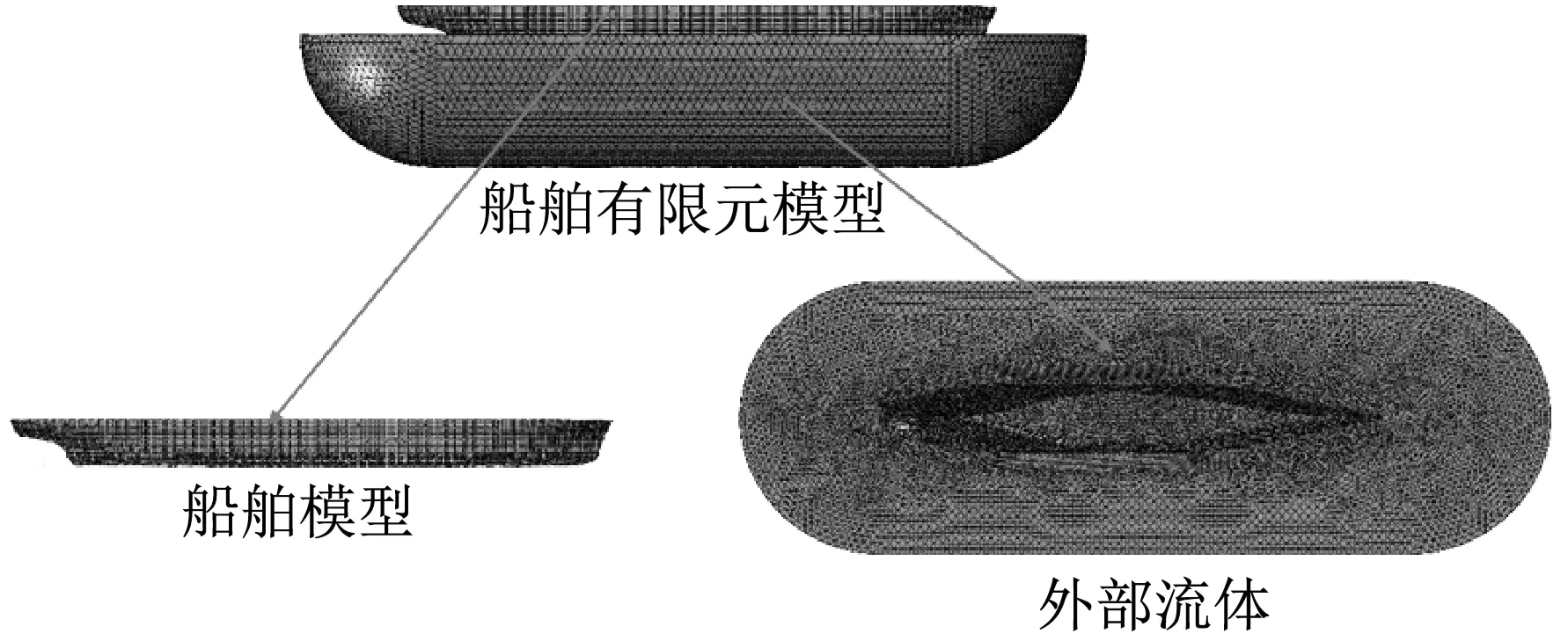
图3 船舶有限元计算模型Fig.3 Finite element model of ship

图4 考察点分布示意图Fig.4 Location diagram of observation points

工程应用中通常以龙骨冲击因子来描述冲击环境与攻击程度、几何尺度之间的关系[16]。在船舶冲击环境计算中，本文计划每艘船舶设置90个工况，如表2所示。其中攻角为30°、60°和90°的工况各30个，冲击因子在0.3～1之间均匀选取，药包质量设置为W/kg，爆心均位于船舯正下方。

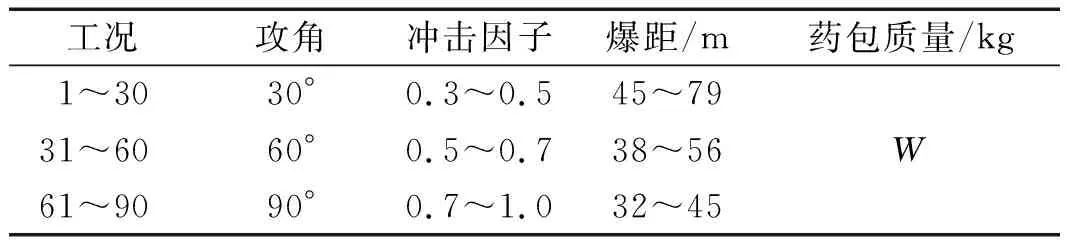
表2 工况设置情况Tab.2 Case lists

通过以上设置，在各艘船舶上选择300～500个考核点，针对每一组仿真结果，分别计算三个方向的冲击响应谱，经过圆整得以设计谱，作为本次研究的对象。如此获得的样本数据共包含120万条左右。

流体与船体结构之间的相互作用是不确定性问题的关键。ABAQUS采用“tie”约束，通过线性动量平衡将结构的位移场和压力场耦合起来。水下爆炸加载方式以一段冲击波载荷作为船舶的加载条件，冲击载荷的时历曲线如图5所示。将上述所取考察点的时历速度曲线作为有限元计算输出，如图6所示。

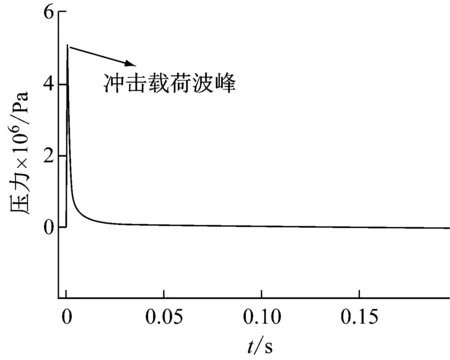
图5 冲击载荷时间历程曲线Fig.5 Time history of shock loading

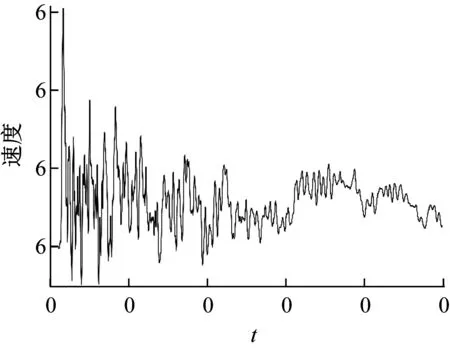
图6 加速度时间历程速度曲线Fig.6 Time history of acceleration

为了更加清晰直观的评估结构的抗冲击性，引入冲击响应谱来描述冲击环境，采用递归滤波法绘制速度谱。某测点冲击响应谱如图7所示。

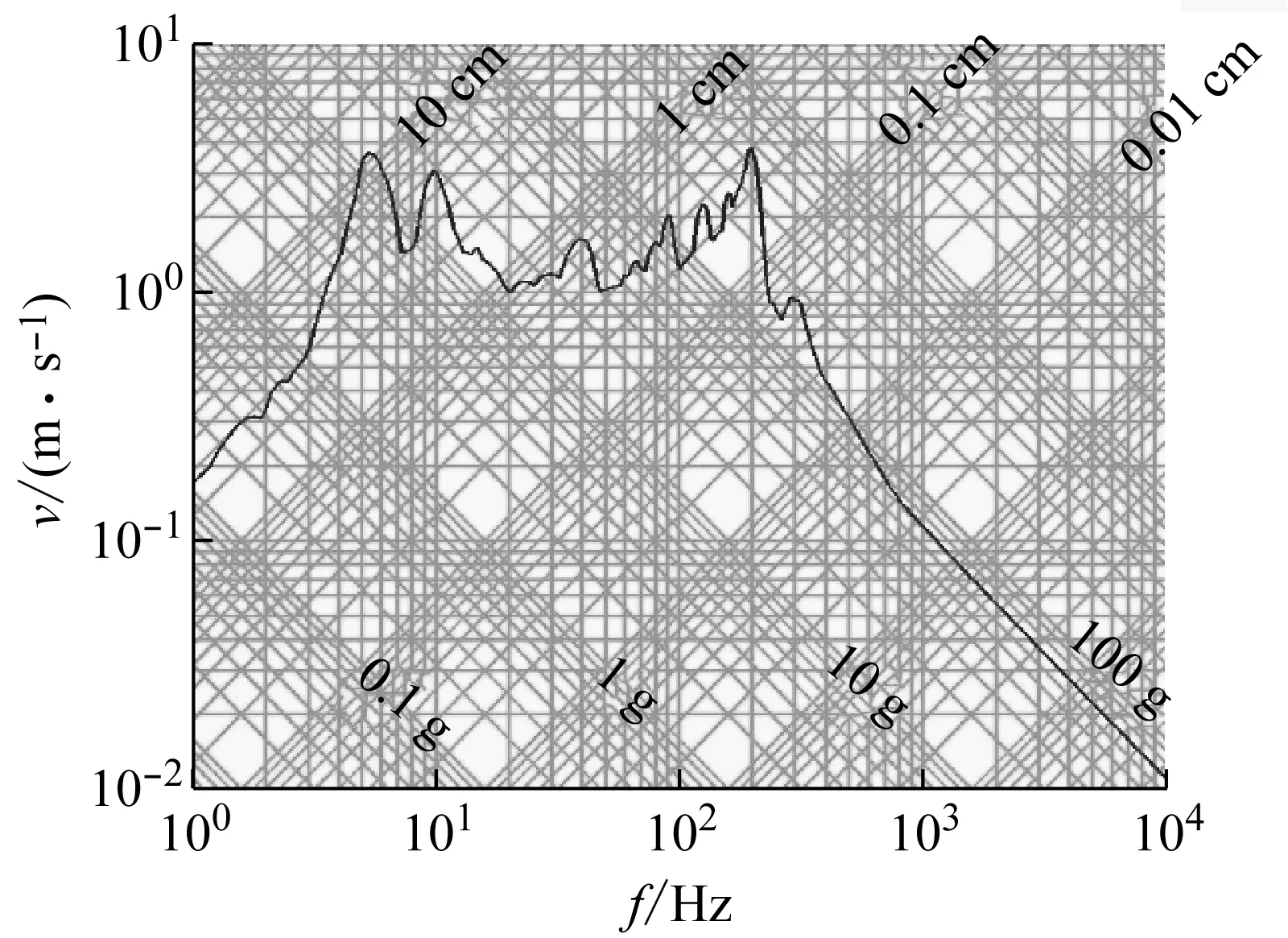
图7 某测点冲击响应谱Fig.7 Shock response spectrum of some point

3 基于聚类算法RBF网络的速度谱数据挖掘

考虑到RBF网络虽学习速度快，但网络结构不易确定[17-19]，本文使用聚类学习算法对搭建的RBF网络进行了优化处理，利用MATLAB软件进行编程和船舶冲击谱速度的预报试验。分别将船舶的主尺度参数、船舶水下爆炸数值仿真的工况设置参数以及考察点的位置坐标作为神经网络的输入参数，以船舶各考察点的谱速度作为输出，通过K均值算法搭建RBF网络。

根据K均值算法算出的中心坐标和拓展常数将训练样本带入隐节点激活函数求出隐层的输出阵，最后利用伪逆法算出输出权值。网络训练流程如图8所示[20]。

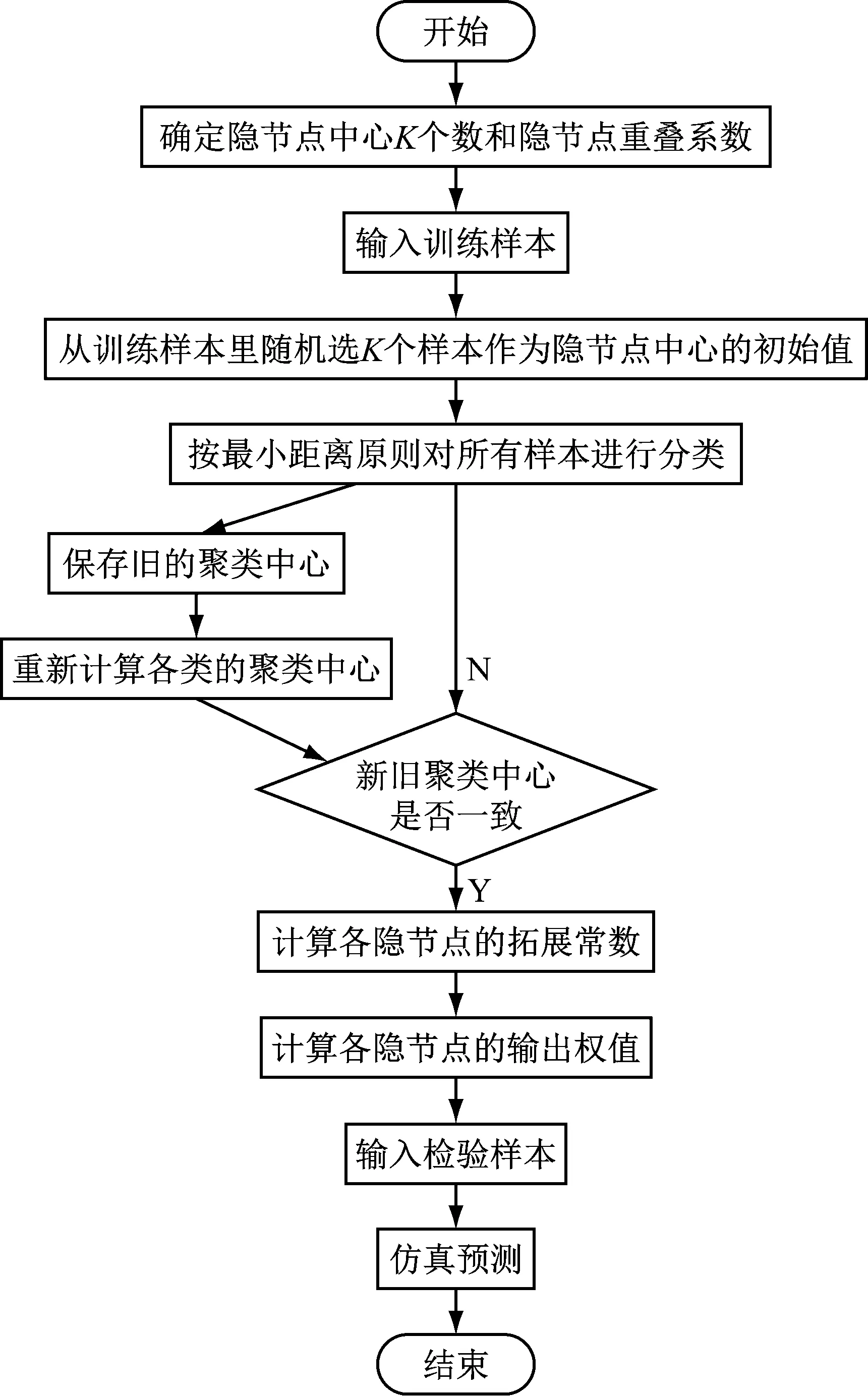
图8 基于聚类算法的RBF网络训练流程图Fig.8 Training flowchart of RBF network based on clustering algorithm

该算法隐节点个数K值和重叠系数λ需要事先给定。因为要把输入样本映射到更高维的空间里，所以K值一定比输入向量的维度大，因为输入维数是8，所以K值至少为9，至多为训练样本的个数360。由于不同问题的最优K和λ是不同的，本文采取试凑的方法，即先确定K值初始值为9，每次试验K值加1。λ值同样如此，初始值为1，之后每次以10递加，观察预测结果找寻规律。

经过多次试验，发现当K值为46时，λ值在区间[70,100]时预测结果最好。这里总结了相关参数对训练过程和预测结果的影响：

(1) 网络对K值十分敏感，当K值在17～45之间时，预测结果和目标结果之间相差很大，并且预测出来的结果不呈现规律性。当K=46或47时，误差突然降低，其中K=46最低；之后随着K增大，误差又开始猛增。

(2)λ值越小，模型对不同甲板考察点的谱速度预报曲线越平滑。随着λ的增大，模型对输入参数会越来越敏感，不同甲板考察点的谱速度预测值之间的差距会逐渐增大。λ值在70～100之间时最合适，当λ再增大时，误差逐渐增大。

训练样本从所建立的船舶冲击环境数据库中随机抽取1 000条数据进行训练，隐节点数K取46，隐节点重叠系数λ取80。对2号船舶的1甲板、2甲板、3甲板上各点的冲击谱速度进行预报，预报考察点位置如图9所示。

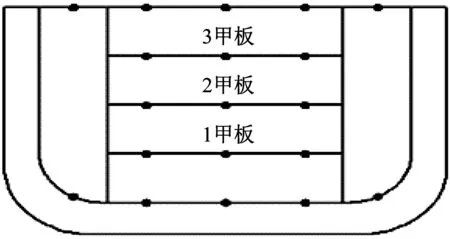
图9 预报考察点位置图Fig.9 Location of prediction points

预报结果与ABAQUS软件水下非接触爆炸冲击仿真数据的相对误差如图10以及表3所示。

表3 不同甲板谱速度预报相对误差对比Tab.3 Relative error of spectrum velocity on various decks

结果表明，K均值聚类算法训练的RBF网络模型对位于不同甲板的谱速度预报结果误差较大，甲板位置自船底沿吃水往上相对误差有增大趋势，究其原因极有可能是由于船体内部结构复杂，其内部能量的传递或损耗规律不甚明确，考核位置越往模型内部选取其网络输入的参数缺陷也就越大；另一方面该次试验用伪逆法算出来的权值绝对值基本在1 000左右，相对较大，而权值偏大其实意味着过拟合，因此会出现误差不稳定的情况；此外，还可能是K均值聚类算法训练的RBF网络对于训练样本数量有一定的要求，训练样本过少时该算法不能对甲板谱速度进行准确预测。总之，对于结构之间的能量传递规律探寻以及将之应用于神经网络的具体实施，以求得冲击谱值的快速预报，则期望后续研究能够得以持续完善。