基于力电耦合模拟的压电悬臂板波激振动获能研究
2022-07-14郭兴文顾水涛信志强
郭兴文, 周 赞, 顾水涛, 信志强
(1. 河海大学 力学与材料学院, 南京 211100; 2. 沿海开发与保护协同创新中心, 南京 211000;3. 江苏省风电机组结构工程研究中心, 南京 211000; 4. 重庆大学 土木与工程学院, 重庆 400030)
近年来,处在海洋环境下小型仪器和海上浮标等设备的供电问题引起了广泛关注[1],由于远离常规电力供应的地点,能量供给以化学能为主,已经越来越成为制约其使用和发展的关键技术难题[2]。更重要的是,它们功率不高,其所处的流体环境就蕴含着大量的可再生能源,如风能、海流能和波浪能等,探索如何高效利用它们所处流体环境实现电能自给已经逐步成为热点问题[3]。
利用流致振动现象捕获流体能量是近年来发展出的使用可再生能源的新形式。振动获能装置结构简单,力电转换效率较高[4],非常适用于解决这类设备的供电问题。其中压电式获能装置制作方便,获能效率高[5],可以直接将压电材料贴合在夹持结构上组成压电式获能装置。流体作用下压电式获能装置的振动可以诱发压电材料的正压电效应,引起压电材料内部正负电荷的规律排布[6],在极化方向上产生电势差,获得电能。而压电悬臂梁(板)因结构简单,是压电式获能装置的常见形式[7]。压电获能装置流致振动获能的主要形式有涡激振动[8-9]、弛振[10]和颤振[11]等。邹鸿翔等[12]设计了一种面内压电振动能量采集装置,建立了机电耦合动力学模型,理论与数值仿真分析结果表明其可显著降低占用空间并能保证较大的输出功率。赵道利等[13]通过试验研究了压电能量收集器的不同截面形状柱体质量块对收集能量性能的影响,可为相关压电获能装置的设计提供借鉴。吴沂宁等[14]针对多种结构的气动弹性振动的能量采集系统,对相关的气动模型进行了总结讨论,指出当前气动模型不能精确计算出结构大振幅下的振动,未来研究中应考虑使用三维非线性气动模型。赵道利等[15]在悬臂式压电能量采集器分布参数模型的基础上,对驰振作用下能量采集器的振动和能量采集情况进一步分析,得到质量块起振风速以及从起振到驰振过程中所采集到的功率解析解。总的来说,涡激振动以卡门涡街为代表,常在液体流体中使用,驰振与颤振常用于气体流体中[16]。
在海洋环境中,由于涡激振动、弛振和颤振等通常用于捕获风能和海流能,且对流速(雷诺数)要求较高,而波浪能能量密度高于风能和海流能[17],为了高效利用海洋环境中的波浪能,少部分学者将流致振动获能拓展到波激振动获能。Xie等[18]将压电悬臂梁竖直放置在线性浅水波中,其一端固支在海床上,用于吸收水平方向的波浪能量。考虑到梁的几何尺寸相对于波浪参数较小,梁的变形较小,采用莫里森公式计算压电悬臂梁上的波浪荷载,基于欧拉-伯努利梁理论建立压电悬臂梁振动数值模型,根据压电理论得到压电材料电能的输出功率。不足之处是压电悬臂梁竖直放置仅适用于水深较小的海况,而且浅水波能量密度较低,此装置经济性略差。为了克服这一缺点,Xie等[19]改用立柱固支在海床上,将压电悬臂梁水平固支在立柱上,用于吸收竖直方向的波浪能量,可适用于浅水波浪和中等水深波浪。考虑到装置的几何尺寸,仍基于上述理论建立其振动获能数值模型。改变关键物理参数后装置输出电功率可以提高到30 W。由此可见,竖直方向的波浪能量较大,后续研究都在此基础上开展。为进一步增加装置的适用范围,Wu等[20]设计了浮式压电获能装置,该装置由立柱、浮筒和立柱上水平固支的压电悬臂梁组成,可以在波浪中做竖向单自由度运动。建立了压电悬臂梁在线性深水波中单自由度振动获能的数值模型后,考虑了压电悬臂梁、立柱和浮筒的几何尺寸变化后对获能效率的影响,结果表明,装置的竖向单自由度运动会降低其获能效率。为了进一步提升获能效率,Viet等[21]设计了由弹簧系统和压电杠杆装置组成浮式获能装置,弹簧系统可以将波浪运动转化为机械振动,压电杠杆装置可以放大机械振动并将其转化为电能。基于拉格朗日-欧拉法模型建立的获能数学模型,通过数值方法求解电能输出功率。结果表明该装置可以放大收集到的机械振动,电能输出功率可以达到103 W。Liu等[22]基于线性波浪理论建立了大尺寸压电悬臂梁在波浪作用下振动获能的数值模型,考虑到波浪的绕射作用,利用入射波理论分析了关键几何参数,得出不同参数取值下装置几何参数对运动、输出电压和功率的影响趋势。
以上研究表明,压电悬臂式获能装置可以有效地吸收波浪能,已开发出一些试验性产品,但是还存在以下不足之处:① 对于真实波浪环境作用下压电悬臂梁的获能研究还不够深入,以上研究在建立压电悬臂梁振动获能方程时都采用二维模型,没有考虑到波浪传播方向对波浪荷载的影响;② 利用解析的方法采用经验公式得到计算波浪荷载,仅有少数文献[22]因为压电悬臂梁尺寸较大而考虑到波浪的绕射作用,而采用数值造波的方法可以提升波浪荷载的求解精度;③ 在振动方程建立过程中没有考虑到压电材料的贴合对基板振动的影响;④ 没有考虑到电压产生过程中,压电效应对压电悬臂梁振动的影响;⑤ 为了简化振动的数值模型,压电悬臂梁上的压电材料只有一片或数片并排贴合,没有考虑到不同位置压电材料对获能的贡献程度。
针对上述问题,本文将压电材料按一定规律排布在基板上,首先采用数值波浪模拟的方法,计算出三维压电悬臂板在深水波中所受的时程荷载;考虑到压电材料的贴合和压电材料压电效应会对压电悬臂板振动产生影响,再采用力电耦合模拟的方法,同时得到板的振动响应和每个压电材料上的输出电压;最后通过对关键物理参数的计算讨论,归纳出对压电悬臂板振动和获能的关键影响因素,分析不同位置压电材料对获能的贡献程度,总结分析波浪运动与振动获能二者的关系,得出提高获能效率的通用方法。
1 问题描述
本文研究的是压电悬臂板在波浪激发下振动获能的机理,如图1(a)所示,一个压电悬臂板被固支在造波水槽中,利用推板造波法从水槽的左端生成波浪,波浪在水槽中单向传播,板在波浪的激发下振动,引发其表面压电材料的形变而产生电能。为方便后续研究,模型中的量采用可变参数模式。

本文研究的流体为气液两相流,气相为空气,密度ρa=1.225 kg/m3,动力黏度μa=1.789 4×10-5Pa·s;液相为水,密度ρw=998.2 kg/m3,动力黏度μw=1.003×10-3Pa·s。考虑到深水波能量密度较大,综合我国黄海和东海的波浪特征[23],将本文波浪取为线性深水波,其波浪参数水深d=40 m,波高H=3 m,波长L=80 m。
压电悬臂板由基板和其上下两侧粘贴的压电材料组成。基板材料为铝合金,密度ρb=2 800 kg/m3,弹性模量E=78 GPa,泊松比ν=0.3。如图1(b)和图1(c)所示,基板长为a(可变),宽b=0.2 m,厚c=0.006 m,基板中性层与静水面的间距定义为压电悬臂板的工作水深h,基板长度方向与波浪传播方向的夹角定义为压电悬臂板的布置角度θ。基板的一端固支,固支端平面的中心点与造波入口的距离为L0。基板的上下两侧粘贴PZT-4压电材料[24],其长a0=0.2 m(与基板的宽b相等),宽b0=0.05 m,厚c0=0.000 6 m。
为了分析不同位置的压电材料对获能的贡献程度,如图2所示,将压电材料间隔排布,在x方向上,每2b0的长度范围为一个获能单元,其上下两侧各粘贴一片压电材料,所以基板的长度a应为0.1 m的整数倍。
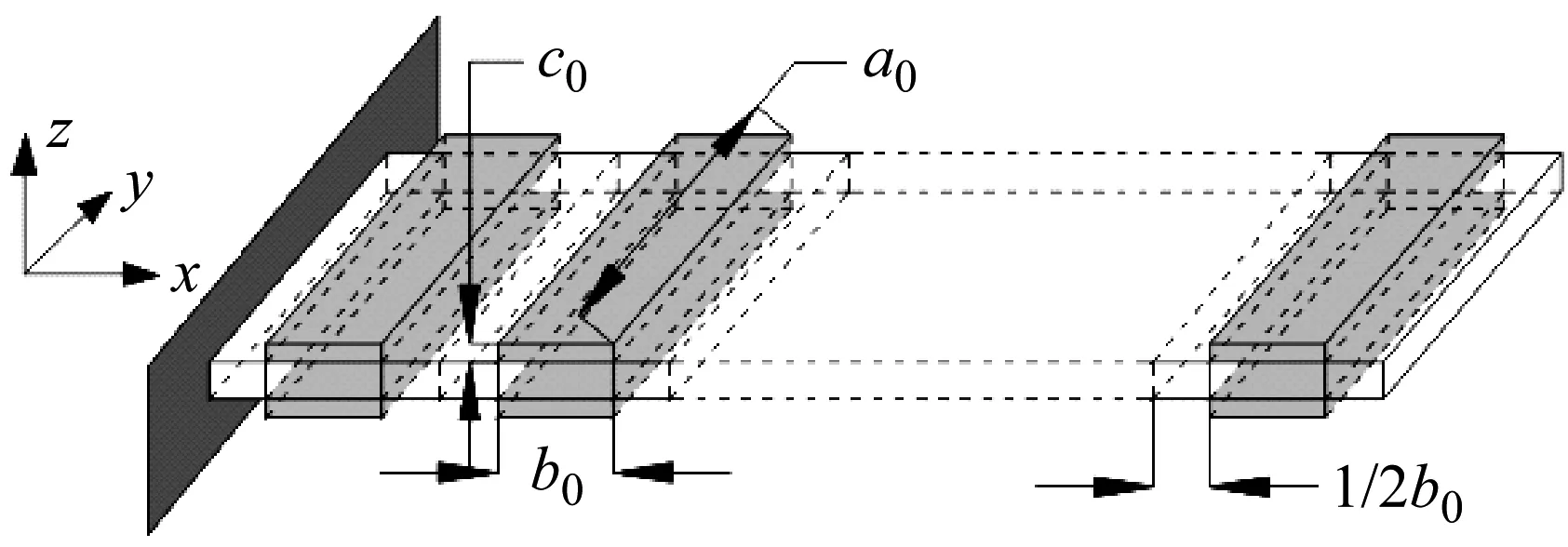
图2 压电悬臂板Fig.2 Piezoelectric cantilever plate
压电材料的密度为ρp=7 500 kg/m3,以+z方向为极化方向,其弹性刚度矩阵C、压电常数矩阵e、介电常数矩阵λ如下
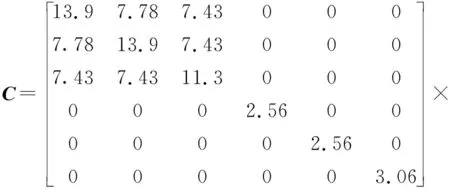
1010N/m2

由于压电悬臂板的几何尺寸与波浪的参数相比较小,其变形对于波浪运动的影响可以忽略不计[25],所以本文先忽略板在波浪作用下的变形,计算出波浪对压电悬臂板的时程荷载;流体计算完毕后,再将此荷载施加到压电悬臂板上,进行力电耦合计算。
2 数值方法
2.1 控制方程
2.1.1 流体控制方程
本文研究的流体是非定常不可压缩均匀流体,控制方程为雷诺平均方程[26],如式(1)和(2)所示
(1)
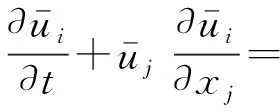
(2)
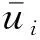
使用RNGk-ε模型[27]模拟湍流,k、ε两方程如式(3)和(4)所示
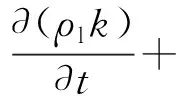
ρlε
(3)

(4)
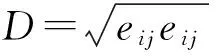
使用流体体积分数(volume of fluid,VOF)模型[28](5)和(6)模拟气液两相流。
(5)
(6)
式中,αk是单元内第k相流体所占质量比。本文中k=1代表空气,k=2代表水。
2.1.2 固体控制方程
压电悬臂板由基板和压电材料组成,其中基板的结构动力学控制方程[29]为式(7)

(7)
式中:ρs1为基板密度;d为位移矢量;g为重力加速度;P=F·S为第一Piola-Kirchhoff应力张量,其中F=I+∇d为变形梯度张量,I为单位张量,S为第二Piola-Kirchhoff应力张量。S如式(8)所示
S=2μE+λtr(E)I
(8)

压电材料的结构动力学控制方程需结合其本构方程导出,压电材料的本构方程[30]为式(9)
(9)
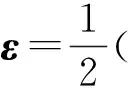
根据Hamilton原理,压电材料的动力学特性可用如式(10)所示的变分方程来表示
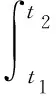
(10)
式中:δ为变分符号;K、U和W分别为动能、势能和外力功;t1和t2分别为振动开始时刻和结束时刻。在不考虑系统阻尼的条件下,式(9)中变量K、U和W的定义分别为式(11)、(12)和(13)。
式中:u、Fb、Fc和Fs分别为作用位移、体积荷载、集中荷载和面荷载;q为面电荷量;ρs2为压电材料密度;v和s为相应作用体和作用面。将式(11)、(12)和(13)代入到式(10)即可得到压电材料的结构动力学控制方程。
基板与压电材料的粘贴面为一层非常薄的界面过渡层,当粘贴情况较好时,认为压电悬臂板的基板和压电材料完全粘合,满足完美界面假设[31],粘贴面两侧物理量在通过粘贴面时是连续的。
在有限元求解中,考虑因几何非线性因素引起固体的大变形,本文采用完全拉格朗日(total Lagrangian,TL)格式描述固体运动过程,所有变量均以初始时刻的位形作为参考位形。
2.2 计算域
2.2.1 流体计算域及边界条件
流体模拟的计算域和边界条件如图3所示。造波水槽长度取440 m,其中0~120 m为造波区和工作区,120~440 m为消波区;高度取50 m,其中静水面以下40 m,静水面以上10 m;宽度取2 m。
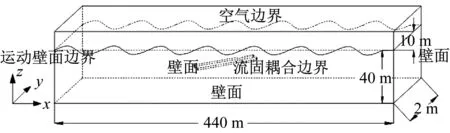
图3 流体计算域和边界条件Fig.3 Fluid computational domain and boundary conditions
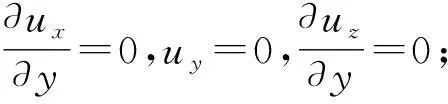

(14)
由于右侧面采用无滑移壁面边界条件,可能会产生波浪反射现象,影响工作区计算精度,所以本文一方面采用了较长的计算域,另一方面在消波区采用渐疏的网格,引入数值阻尼进行消波。
2.2.2 固体边界条件
压电悬臂板固定端边界条件为位移d1=d2=d3=0、转角θ1=θ2=θ3=0;其余表面都为流固耦合边界;基板的上下表面为零电势边界V=0,上侧压电材料的上表面和下侧压电材料的下表面添加耦合电压,作为等电势面求解。
2.3 数值验证
2.3.1 流体数值验证
为了确保压电悬臂板波浪荷载求解准确,首先要进行造波模拟的准确性验证。造波模拟计算总时长为50 s,约为7个波浪周期,计算结束时波面如图4所示。

图4 数值波浪模拟(浅色相为空气,深色相为水)Fig.4 Numerical wave simulation
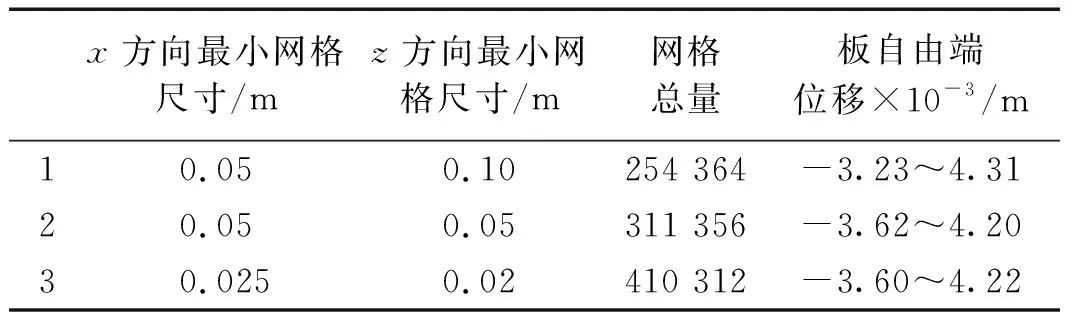
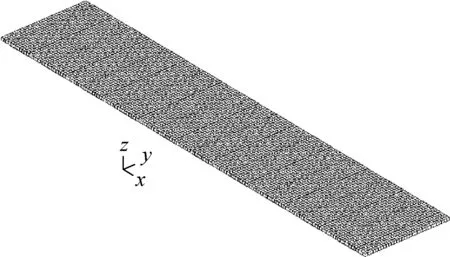
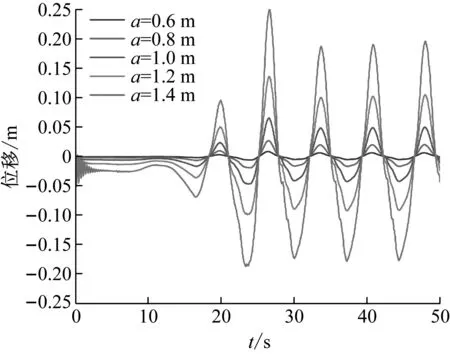
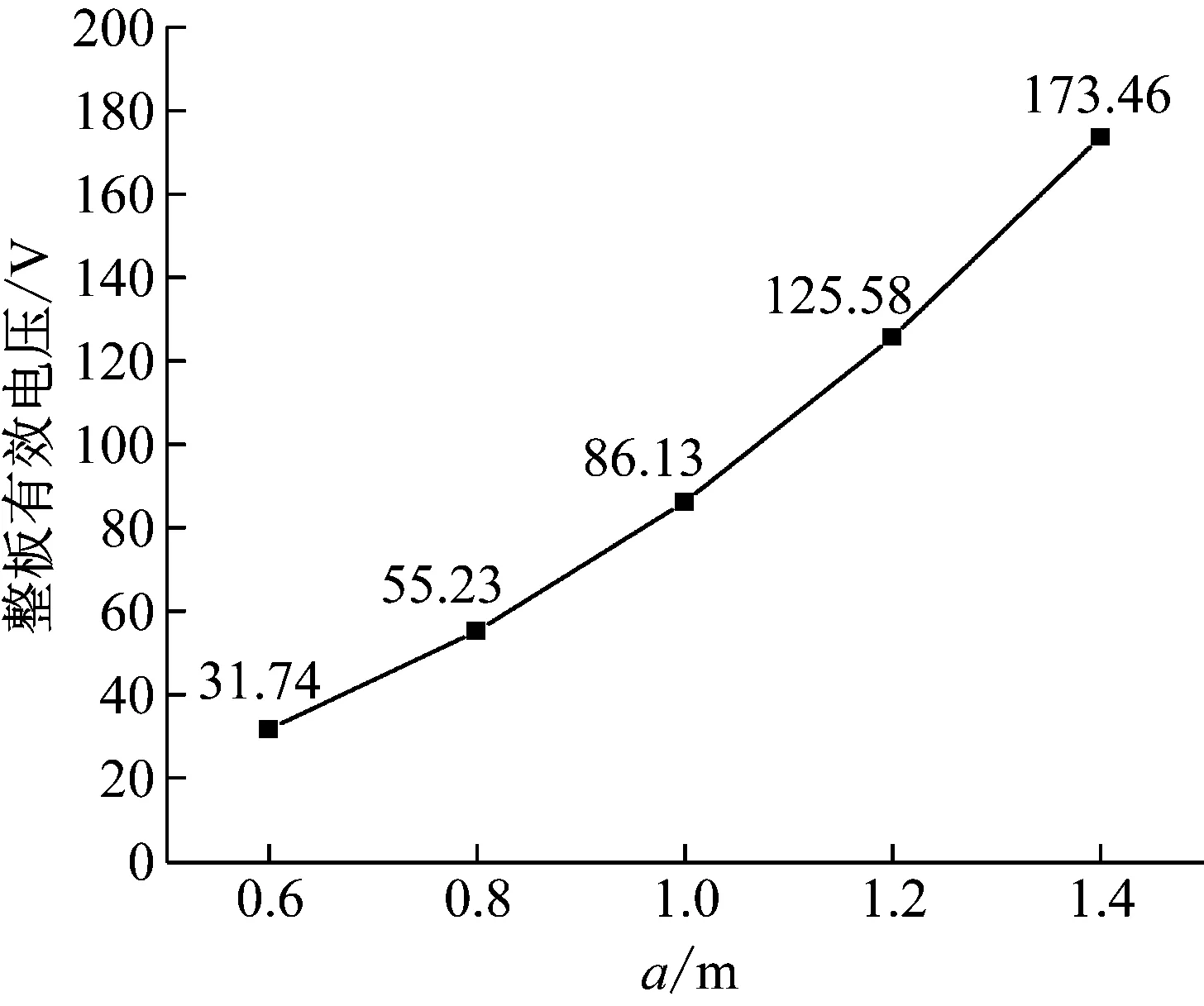
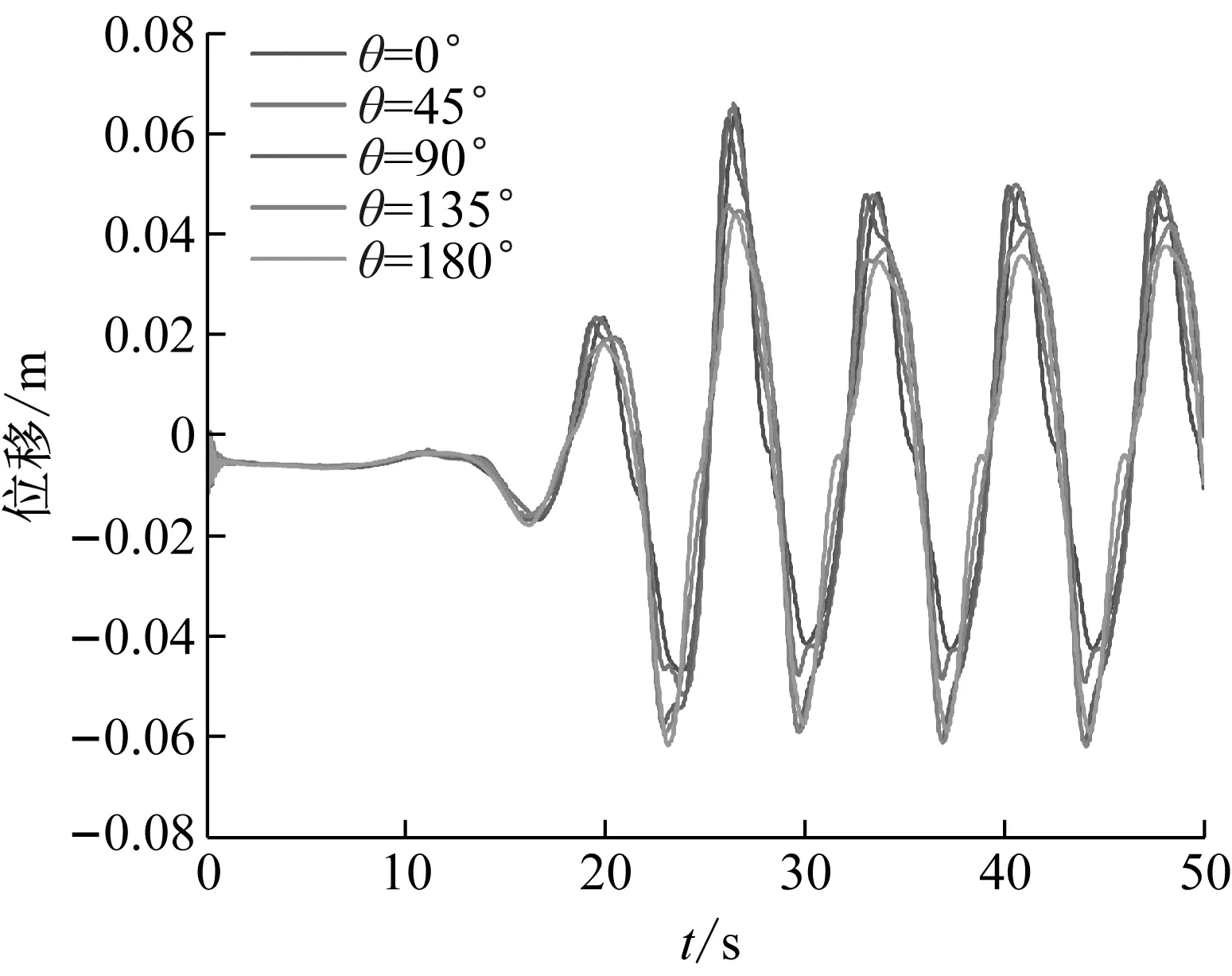
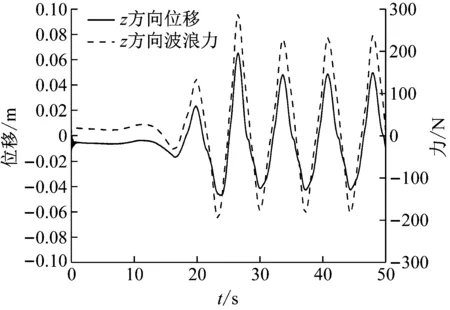
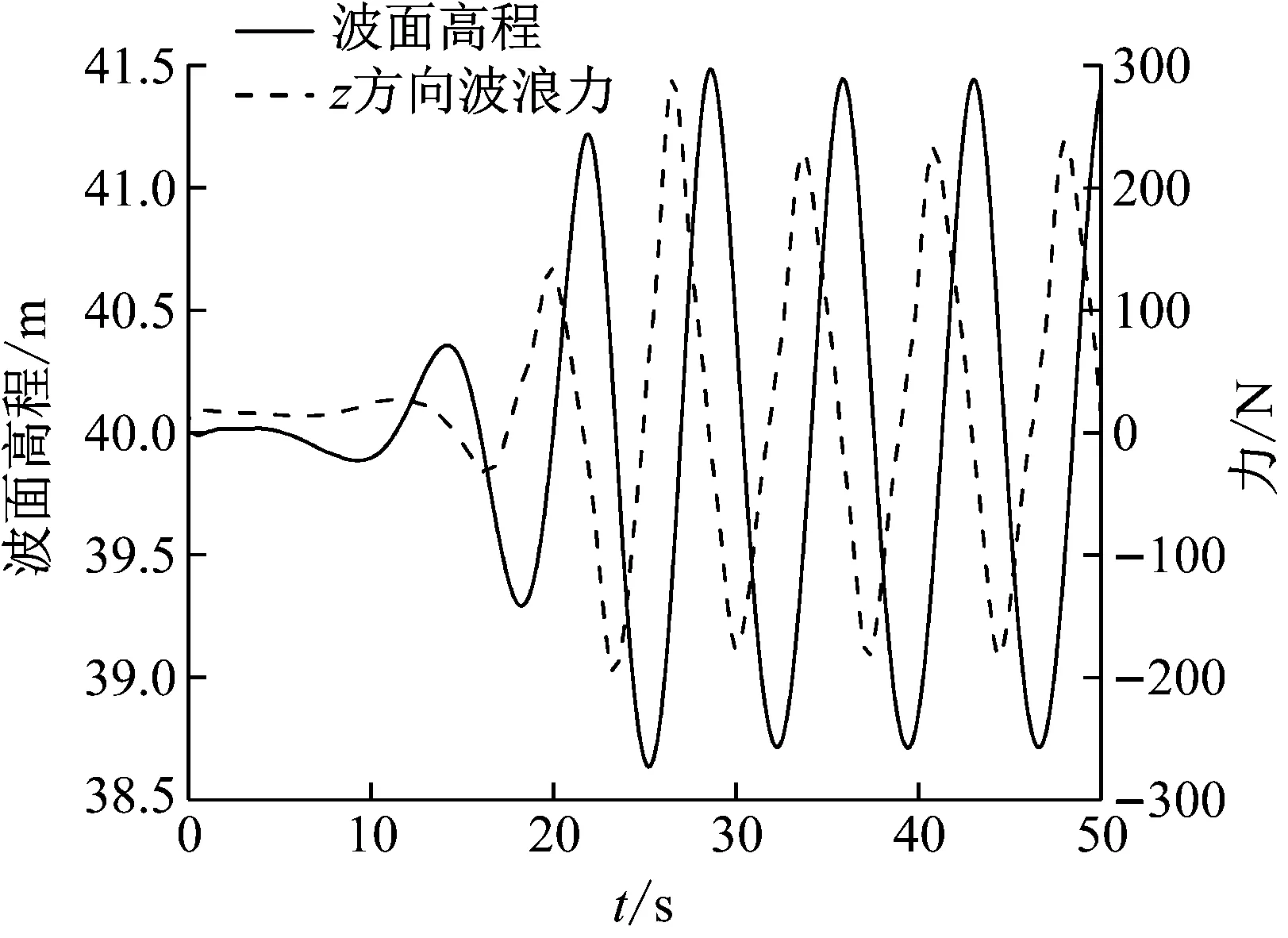
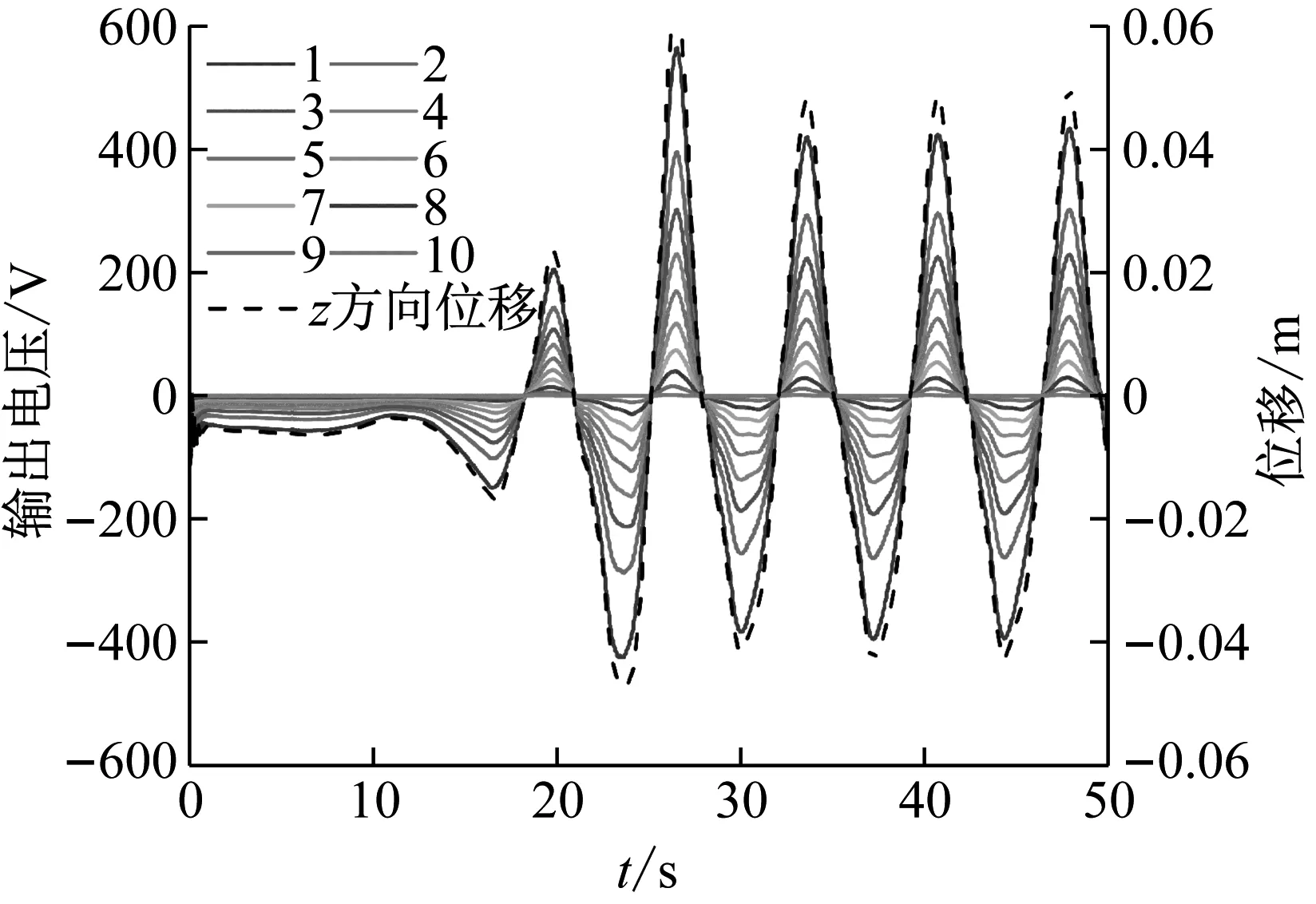
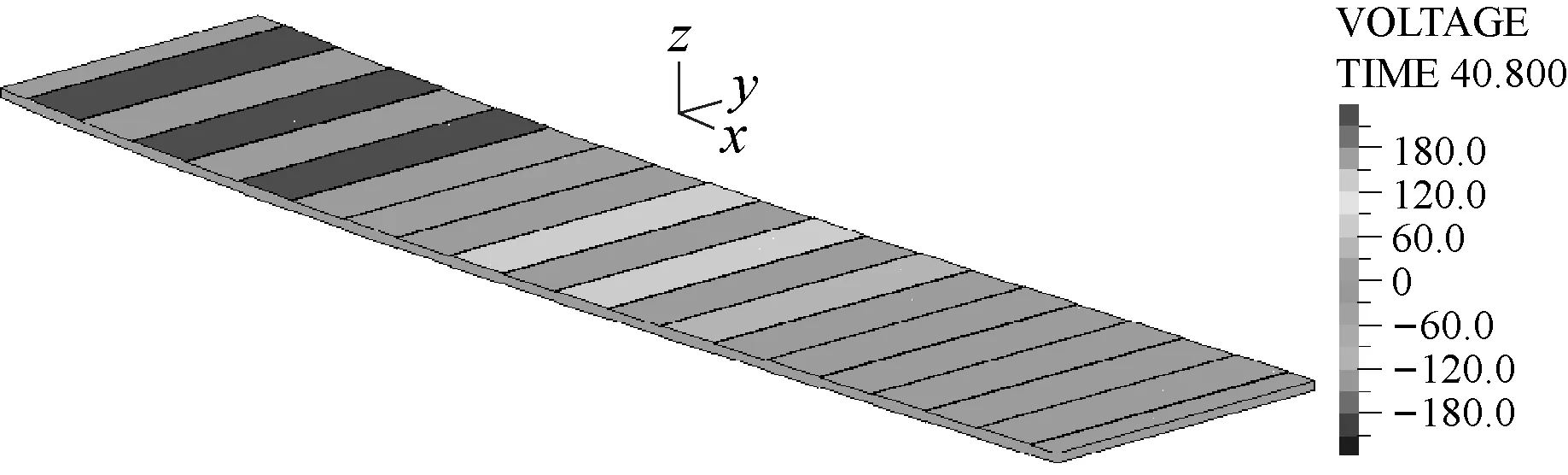
因为后续研究需确保工作区(40 m 从图4和图5中可以看出,在造波区和工作区内波浪得以较好地生成;在消波区内,波高被逐步削减,最终近似形成静水面。在造波区和工作区内,尤其在x=40 m和80 m处,数值造波波高与理论波高较为贴合,这表明本文数值造波精度较高;另外,从工程角度上讲,当波浪在x方向上传播2~3个水深的距离后,由推板产生的立波的影响完全可以忽略[34],因此为了兼顾数值造波的准确性,后续压电悬臂板固支端平面的中心点与造波入口的距离L0取为80 m。 2.3.2 固体数值验证 为了确保压电悬臂板力电耦合计算准确,选取如图6所示算例做验证[35]。 图6 固体数值验证算例计算简图Fig.6 Numerical validation example of solid 压电悬臂板的基板为铝,密度为2 800 kg/m3,弹性模量为75 GPa,泊松比为0.33;压电材料同为PZT-4压电材料,以+z方向为极化方向,基板左端固定,自由端施加-z方向、大小为1 N的力,基板与压电材料接触面为零电势边界条件,压电材料的上表面施加耦合电压,作为等势面计算。计算结果如表1所示。 表1 固体数值验证算例计算结果Tab.1 Numerical validation results of solid 从表1中可以看出,本文压电悬臂板力电耦合模拟计算方法准确,软件使用无误。 2.3.3 网格无关性验证 为保证本文数值计算准确,选取参数h=2 m、a=1 m、θ=0°进行网格无关性验证。如图7所示,流体网格为结构网格。本文理论波面高度范围为z=38.5~41.5 m,为了能准确模拟出波面,在z=38~42 m的范围内加密网格,网格尺寸不超过H/30=0.1 m;在造波区和工作区内,x方向网格尺寸不超过L/50=1.6 m,在消波区采用了渐疏的网格。此外,在波高范围内、板周围流场范围内均进行了加密,详细尺寸如表2所示。 (a) 流体网格正视图 (b) 流体网格局部俯视图图7 流体网格Fig.7 Fluid grid system 表2 流体网格无关性验证结果Tab.2 Grid validation results of fluid 选取三种不同疏密程度的流体网格,此时固体计算采用同样的网格,分别计算得到板自由端z方向位移见表2。 可见用中等疏密程度的流体网格固体所受波浪荷载已很准确。流体计算都使用此网格,固体网格如图8所示,为全六面体网格,再选取三种不同疏密程度的固体网格,分别计算得到板自由端z方向位移如表3所示。 图8 固体网格Fig.8 Solid grid system 表3 固体网格无关性验证结果Tab.3 Grid validation results of solid 可见用中等疏密程度的固体网格对压电悬臂板进行固体计算已很准确。 在本文的后续计算中,都采用上述的中等疏密程度的流体网格和固体网格。 将压电悬臂板从固定端到自由端所有获能单元分别编号为1~n,用获能单元质心到固定端平面的距离表示其所在位置。 在力电耦合模拟完成之后,得到每个获能单元上下表面压电材料的输出电压曲线。用输出电压曲线的均方根值来描述电压的有效值(有效电压),如式(15)所示 (15) 式中,Vi(t)为第i个获能单元压电材料的输出电压曲线,积分时间取电压曲线较为稳定的时间段。 而压电悬臂板整板的有效电压为所有获能单元有效电压的平均值,可由式(16)计算得出 (16) 式中:n为获能单元总数;t为上侧压电材料;b为下侧压电材料。整板有效电压的大小可以用来衡量整板获能效率的高低。另外,从后续计算结果中可以得出,由本文压电材料的粘贴方式决定,上下侧压电材料有效电压几乎相等,后续仅需讨论上侧压电材料的有效电压。 本节先针对压电悬臂板的工作水深h、基板的长度a和压电悬臂板的布置角度θ这三个参数进行一系列的数值模拟计算,从中归纳出这三个参数对压电悬臂板振动规律和获能模式的影响规律,总结分析了波浪运动与振动获能二者的关系,从而得出提高获能效率的方法。 3.1.1 压电悬臂板的工作水深h 将θ取为0°,a取为1.0 m,h分别取1 m、2 m、3 m、4 m和5 m。 图9给出了h不同取值时板自由端z方向位移曲线,从中可以看出,板的振动频率都近似相等,随着工作水深h的不断增加,板自由端z方向振幅不断减小。当h=2 m、3 m、4 m和5 m时,正负位移幅值相差不大,振动较为对称;而当h=1 m时,板自由端正负位移极值相差较大,正位移幅值比负位移幅值大很多。 图9 h不同取值时板自由端位移变化图Fig.9 Displacement of the free end of the plate with different h 由于本文波高H=3 m,理论上波谷最低可以到达自由水面以下1.5 m(H/2)处。当h>H/2时,板完全浸没在水中;当h 图10和图11分别给出了h不同取值时各个压电材料的有效电压值和整板的有效电压值。从中可以明显看出,h取值越小,整板的输出电压越高,且靠近固定端的压电材料能获得更高的能量。但当h 图10 h不同取值时不同位置处压电材料有效电压变化图Fig.10 Effective voltage of the piezoelectric materials at different positions with different h 图11 h不同取值时整板有效电压变化图Fig.11 Effective voltage of the plate with different h 从图中可以计算得出前两个获能单元获能占比达到50%,前五个获能单元获能占比接近90%。 3.1.2 基板的长度a 将h取为2 m,θ取为0°,a分别取为0.6 m、0.8 m、1.0 m、1.2 m和1.4 m。 图12给出了a不同取值时板自由端z方向位移曲线,从中可以看出板的振动频率都近似相等。随着板长a的增大,板自由端z方向位移在显著增大。这是因为一方面,板接受波浪荷载的面积不断增加,有更多的波浪能转化为板的应变能;另一方面,板的长宽比减小,从而降低了板的固有频率,使板更容易振动变形。 图12 a不同取值时板自由端位移变化图Fig.12 Displacement of the free end of the plate with different a 对板做模态分析,如表4所示,可以看出板的一阶固有频率在不断降低,且一阶固有振型都为z方向的弯曲振型,这就使得板长a增加时,板的一阶固有频率在不断接近波浪荷载的频率(0.139 Hz),板的振动形态逐步接近一阶振型,使得板端位移在显著增大,从而获能效率不断增加。 表4 a不同取值时板的固有频率Tab.4 Natural frequencies of the plate with different a 图13和图14分别给出了a不同取值时各个压电材料的有效电压值和整板的有效电压值。从中可以看出,当板长a增加时,距固定端相同距离的压电材料电压增长明显,板上每一个获能单元的获能效率大大提升,这就引起整板有效电压大幅度增加,获能效率提高明显。 图13 a不同取值时不同位置处压电材料有效电压变化图Fig.13 Effective voltage of the piezoelectric materials at different positions with different a 图14 a不同取值时整板有效电压变化图Fig.14 Effective voltage of the plate with different a 从图中还可以计算得出前两个获能单元获能占比达到50%,前五个获能单元获能占比接近90%。 本文所选取压电材料强度极限约为100 MPa[36],而基板的强度极限约为200 MPa。本文图15给出了a不同取值时压电材料的等效应力(Von Mises应力)图,从图中可以看出,当a=1.4 m时,靠近固定端的压电材料应力极值约为95.6 MPa,还没有达到强度极限,但此时已容易发生强度破坏,所以增大板长a提高获能效率需考虑压电材料的强度。 (a) a=1.2 m (b) a=1.4 m图15 压电材料的等效应力图(Pa)Fig.15 Effective stress of the piezoelectric materials (Pa) 3.1.3 压电悬臂板的布置角度θ 将h取为2 m,a取为1.0 m,θ取0°、45°、90°、135°和180°。 图16给出了θ不同取值时板自由端z方向位移图,从图中可以看出,板的振动频率都近似相等。θ=0°和45°时,板自由端的+z方向振幅比-z方向振幅略大,θ=135°和180°时,板自由端的+z方向振幅比-z方向振幅略小,而当θ=90°时,板自由端+z和-z方向振幅近似相等。 图16 θ不同取值时板自由端位移变化图Fig.16 Displacement of the free end of the plate with different θ 从图16中还可以看出,θ=0°与θ=180°、θ=45°与θ=135°时,板自由端净位移分别近似相等,相对而言,θ=90°时,板端净位移数值最大,从而获得的能量最大。 图17和图18分别给出了θ不同取值时各个压电材料的有效电压值和整板的有效电压值。 图17 θ不同取值时不同位置处压电材料有效电压变化图Fig.17 Effective voltage of the piezoelectric materials at different positions with different θ 图18 θ不同取值时整板有效电压变化图Fig.18 Effective voltage of the plate with different θ 从图中可以看出,靠近固定端的压电材料均能获得更高的能量,其中θ=90°与θ=0°、45°、135°和180°相比,板上相同位置的各个获能单元均获得了最大的能量,所以整板的有效电压最高。而从图17和图18中还可以看出,θ=0°和180°、θ=45°和135°时获得了几乎相等的能量,这是因为板自由端净位移数值大致相等,这由板所受波浪力的规律决定。从图中仍可以计算得出前两个获能单元获能占比达到50%,前五个获能单元获能占比接近90%。 不同θ取值时板沿长度方向流体压力分布图如图19所示。当θ=90°时,如图19(a)中所示,其上下表面分布的压力分布比较均匀,压力梯度垂直于板平面,板可以获得最大的合力,这是因为板各个获能单元处的uz大小较为一致,所以接收的波浪力大体相同;当θ≠90°时,如图19(b),板上下表面压力分布不均匀,压力梯度与板平面斜交,这就导致板无法获得最大的合力,而这是因为各获能单元处uz大小不均匀,部分获能单元接收的波浪力有所超前或滞后。 (a) θ=90° (b) θ=0°图19 板沿长度方向的压力云图Fig.20 Pressure coutours along the length of plate 由3.1的计算结果可以看出,压电悬臂板自由端z方向位移规律大体相同,振动频率近似相等,板在波浪激发下的振动表现为受迫振动,所以板端净位移越大,其获能效率越高。 3.2.1 波浪力与板自由端位移的关系 以参数h=2 m、θ=0°、a=1 m的算例为例,图20给出了板受力曲线和板自由端z方向位移曲线。从图中可以看出,受力曲线和位移曲线走势基本同步。在较早的时间内,波浪还没有传播到板处,板只受+z方向的浮力和-z方向的重力作用,位移表现为负向,这是因为板的密度比水大,其重力比浮力大;从30秒开始,板处的波浪运动变得稳定,其振动也稳定下来,板在波浪中的振动呈现典型的周期性,且板振动频率与波浪频率保持一致。由表5可知,本文中板的一阶固有频率均为几赫兹以上,一阶振型都为z方向的弯曲振型,而波浪荷载频率为0.139 Hz,所以板还没有被激发出一阶振型。 图20 板受力曲线与板自由端位移曲线Fig.20 Fluid force and the displacement of the free end of the plate 3.2.2 波浪力与波面形态的关系 图21给出了板受力曲线和板处波面高程曲线,从中可以看出,受力曲线与板处(x=80 m)波高曲线相比有约为T/4的相位差,波浪力最大值在从波谷到波高爬升中取得,波浪力最小值在波高到波谷的下降中取得。 图21 板受力曲线与板处波高曲线Fig.21 Fluid force and the wave height near the plate (17) (18) 此例中,压电悬臂板的固定端位于(x,z)=(80,38)处,可以用此点处的速度规律描述板附近流体的速度规律。如图22所示,板处流体速度分量ux与uz恰好也存在T/4的相位差。 图22 板附近流体理论速度Fig.22 Theoretical velocity near the plate 综合图20、图21和图22可以得出,板受力曲线和自由端位移曲线都与uz正相关,而波高曲线与ux正相关。板的受力与否与流动方向有关,力的大小与流速大小有关。z方向的流体速度带来的动压能量是板在z方向受力和振动的主要原因。 波浪传播方向上水质点速度分布图如图23所示。当板处波面在波峰位置①或波谷位置②时,ux达到峰值,而uz=0,板周围流体质点沿x方向运动,此时板上z方向受力为0,板自由端不发生位移,板几乎处于水平状态;板处波面在波谷到波高爬升位置③或在波高到波谷的下降位置④时,ux=0,uz达到峰值,板周围流体质点沿z方向运动,此时板的受力(或自由端位移)也达到峰值。这也正解释了为什么板的受力(或自由端位移)曲线与板处波高曲线相比有T/4的相位差。 图23 一个波长范围内水质点的速度分布Fig.23 Velocity distribution of fluid in the range of wavelength 式(18)中x取80 m,z取39 m、38 m、37 m、36 m和35 m,分别得到不同工作水深h=1 m、2 m、3 m、4 m和5 m处uz的时程曲线如图24所示。 图24 h不同取值时流体竖向速度变化图Fig.24 Vertical velocity of fluid with different h 从图24中可以看出,越靠近自由水面,水质点运动越剧烈,从而可以产生更高的能量,引发更大的板端位移,这正解释了3.1.1中得到的规律。 由3.1中的计算结果可知,不同位置处压电材料有效电压变化规律大体相同,都表现为从固定端到自由端,板表面压电材料的输出电压逐渐降低。 以h=2 m、θ=0°、a=1 m的算例为例,图25给出了每个压电材料的输出电压曲线和板自由端z方向位移曲线,从图中可以看出可以看出每个获能单元输出电压曲线与其板自由端位移曲线呈正相关,越靠近自由端,获能单元输出电压越低。 图25 压电材料输出电压曲线与板自由端位移曲线Fig.25 Output voltage of the piezoelectric materials and the displacement of the free end of the plate 当板向上弯曲时,基板的中性层应力为零,中性层以上受到压应力作用,中性层以下受到拉应力作用,基板表面的上压电材料在xoy平面内同样会受到压应力作用。如图26所示,由于上压电材料的下表面电势为零,极化方向为+z方向,所以诱发上压电材料的上表面产生正电势。 (a) 板向上弯曲 (b) 板向下弯曲图26 板弯曲时压电材料产生电压示意图Fig.26 Voltage generated by the piezoelectric materials when the plate is bending 而基板上下侧的压电材料极化方向相同,但是承受的应力反向,并且零电势的边界不同,所以在同一个获能单元上,基板上侧压电材料的上表面和下侧压电材料的下表面会产生大小几乎相等的电压,输出电压曲线几乎重合,有效电压几乎相等。 在基板长度方向上,从固定端到自由端,板的形变逐渐降低,其上的拉压应力也逐步趋近于零,所以压电材料的输出电压也逐步趋近于零,这也正解释了3.1得到的规律。 由3.1的计算结果还可以得出,每个获能单元有效电压占总电压的比例规律一致,都表现为前两个获能单元获能占比达到50%,前五个获能单元获能占比接近90%,实际使用中需尽量将压电材料布置在固定端附近。 本文通过数值模拟的方法,研究了压电悬臂板在线性深水波激发下的振动获能机理。通过波浪数值模拟和压电悬臂板力电耦合模拟,归纳出压电悬臂板的工作水深h、基板的长度a和压电悬臂板的布置角度θ这三个参数对板振动规律和获能模式的影响规律,分析并总结了波浪运动与振动获能二者的关系,得出压电悬臂板在线性深水波激发下的振动获能机理,结论如下: 对于本文参数选取来说,波浪荷载频率小于压电悬臂板的一阶固有频率,板没有被激发出一阶振型,板的振动周期与波浪周期保持一致,板在波浪中的振动表现为典型的受迫振动,所以板自由端振幅越大,其获能效率越高。在板弯曲振动过程中,压电材料也会产生相同周期的电压,从而将波浪能转化为电能。经过计算,本文压电悬臂板的输出电压可以满足海洋中部分设备的用电要求。 压电悬臂板自由端的位移曲线与其所处位置的波高曲线有四分之一个波浪周期的相位差,这是由波浪水质点的运动规律引起的。板所处位置附近的竖向波浪运动越剧烈,板的振幅越大,板上的压电材料可以输出更高的有效电压。为了充分利用波浪中水质点的动能,提高整板的获能效率,板须布置在波谷以下适当位置;板的长度方向应垂直于波浪传播方向;在保证压电材料不发生破坏的前提下,可以增大板长宽比,降低其固有频率以获得较大的板端振幅。 压电悬臂板上各个压电材料的获能效率与其所在位置基板的形变大小成正相关,越靠近固定端,压电材料获能效率越高。考虑到材料成本,因板自由端压电材料的获能效率较低,在实际使用中可以仅保留固定端附近的压电材料。




3 结果与分析
3.1 关键物理参数对压电悬臂板获能效率的影响及分析











3.2 压电悬臂板的振动规律



3.3 压电悬臂板的获能模式

4 结 论
