基于多时频曲线提取广义特征的变转速轴承故障诊断
2022-07-14张宏立
肖 飞, 张宏立, 马 萍, 王 聪
(新疆大学 电气工程学院, 乌鲁木齐 830000)
滚动轴承是旋转机械中的重要部件,由于复杂的工作环境和运行状态(急剧变转速、变负载等),使其在实际生产环境中极易受到损坏。根据相关资料:旋转机械中的超过30%的机械故障是由轴承故障引起的[1]。而且,在实际生产过程中,机械设备常在变转速工况下运行。因此研究变转速工况下的滚动轴承故障诊断具有重要的生产实践意义。
变转速工况下,滚动轴承振动信号呈现的时变非平稳特性使得故障特征难以提取。近年来,国内外许多学者针对变转速工况下的滚动轴承故障诊断开展了大量研究[2-5]。较为典型的方法是基于阶次跟踪的轴承故障诊断技术,其核心思想是将角域上的信号重采样得到循环平稳的信号,硬件阶次跟踪和计算阶次跟踪都要求设备安装转速计来获取转速,这增加了空间和经济成本[6]。因此,国内外学者开始研究无转速计下的阶次跟踪方法,并提出基于瞬时频率估计的转速计算方法[7-8]。此外,阶次跟踪方法还存在一些局限性,其在信号重采样的过程中存在幅值误差、包络畸变以及计算复杂等问题[9-10]。
Olhede等[11]提出的广义解调方法,是一种可以将非线性非平稳信号转换为线性平稳信号的方法。刘东东等[12-16]将其应用到旋转机械的故障诊断中。由于原始广义解调算法只能对原始信号中的单一分量进行单次解调变换,难以处理多分量信号。因此有学者对广义解调进行了改进,提出了迭代广义解调算法[17]。迭代广义解调算法存在一些不足,由于其对振动信号循环多次进行解调变换,导致结果出现频谱混叠[18]。
Huang等[19]提出了一种基于快速路径优化的多时频曲线提取(multiple time-frequency curve extraction, MTFCE)方法,能够将包络时频图中的瞬时故障特征频率(instantaneous fault characteristic frequency, IFCF)和瞬时转频(instantaneous shaft rotational frequency, ISRF)曲线提取出来,利用IFCFs与ISRF的比值来描述提取的曲线之间的关系。因此,可通过比值与分量信号特征系数的比较来实现分量信号的特征提取。在变转速振动信号中,由于低转速下时频图中转频和故障冲击成分被淹没在噪声中,导致曲线之间比值误差较大,使得无法通过比值对故障特征进行有效提取。
综上所述,为解决变转速滚动轴承故障信号由于时变非平稳特性、故障冲击幅值淹没在噪声中,导致故障诊断困难的问题,提出一种新的基于多时频曲线提取广义特征的变转速轴承故障诊断方法。利用MTFCE从包络时频谱中提取IFCFs和ISRF,基于假设思想,根据广义解调理论计算变转速轴承发生故障时的广义特征指标,再构建量化诊断模型进行故障诊断。该方法相较于迭代广义解调方法无需对信号进行解调变换,避免了多次解调导致的频谱混叠问题,同时无需利用曲线的比值进行诊断,提高了诊断的准确率。仿真信号和实例分析结果证明了所提方法的鲁棒性和有效性。
1 算法部分
1.1 多时频曲线提取算法
多时频曲线提取算法是一种基于快速路径优化的时频曲线提取算法,能够将时频图中的IFCFs和ISRF曲线提取出来。
假设信号x(t)经过短时傅里叶变换后的时频表达(time-frequency representation, TFR)为X(τ,f),其中τ为时间变量,f为频率变量。快速路径优化算法可从X(τ,f)中提取出T-F曲线fp(τ)。定义TFR中时间τn处的峰值表示为Np(τn),第m个峰值对应频率为vm(τn),第m个峰值对应的TFR幅值为Qm(τn)。
(1)
如果X(τ,f)的时间跨度为[τ1,τ2,…,τN],路径优化可描述为
(2)
其中mc(τN)确定在时间τn处提取的峰值,F[]为优化选择支持函数,{m1,…,mN}表示沿时间跨度的峰值数数列。文献[20]提出了一种只依赖于具有支持函数的有限个前向点的快速路径优化算法,算法具体步骤如下所示
(3)
其中:
(4)
(5)
m[]=perc0.5[],IQR[]=perc0.75[]-perc0.25[]
(6)
其中fd(τn-1)是τn-1处的候选峰值的频率,fd是在时间[τ1,…,τn-1]的一系列候选峰值的频率。Δfd是fd的导数。m[]表示一系列数的中位数,IQR表示四分位距。percp表示序列的第p个分位数。λ1和λ2是惩罚因子,可以取1。权函数w1()和w2()分别用于抑制脊线频率值和其导数的非典型变化。
快速路径优化问题可表示为
forn=1,…,N,m=1,…,Np(τn)
andk=1,…,Np(τn-1)
(7)
其中,q(m,τn)用来表示前一时刻τn-1的峰值应与当前时刻τn的峰值相联系。U(m,τn)是有助于优化的中间向量。
将最后计算结果U(m,τn)最大的峰值作为提取曲线的终点,然后基于q(m,τn)的结果向前追踪峰值提取出整条曲线。
基于快速路径的多时频曲线则是在提取出一条时频曲线后,将该条曲线从时频图中删去,再重复应用快速路径优化算法提取下一条时频曲线,直到提取曲线数量达到预设的值。
1.2 基于假设思想的广义特征指标计算
变转速下,滚动轴承的IFCFs在包络时频图中表现出明显的峰值,且IFCFs与ISRF存在固定的比例关系,这个比例关系与轴承的故障特征系数相关。
广义解调可通过选择合适相位函数可以将时频图中特定的曲线转换成平行于时间坐标轴的直线,通过频谱图可看到与该曲线对应的突出峰值。该峰值与轴承故障联系紧密。
因此,基于假设思想,假设发生故障时的该峰值为变转速轴承故障的广义特征指标。可利用广义解调理论定义广义特征指标。
广义解调理论的基本思想是对信号x(t)进行广义傅里叶变换
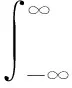
(8)
式中,s0(t)表示随时间变化的实值函数。
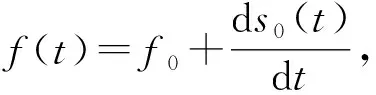
变转速滚动轴承发生外圈、内圈和滚珠故障时对应的故障特征系数Fo,Fi和Fb计算如下所示
(9)
(10)
(11)
式中:fo,fi和fb分别表示外圈、内圈和滚珠故障特征频率;n为滚动轴承滚珠个数;fr为轴承转频;D为滚动轴承节圆直径;d代表滚珠直径;α为接触角。
假设预设转频方程为
y=c0+c1t+c2t2+…+cmtn
(12)
由广义解调变换理论,提出解调变换后的故障广义特征指标如表1所示。
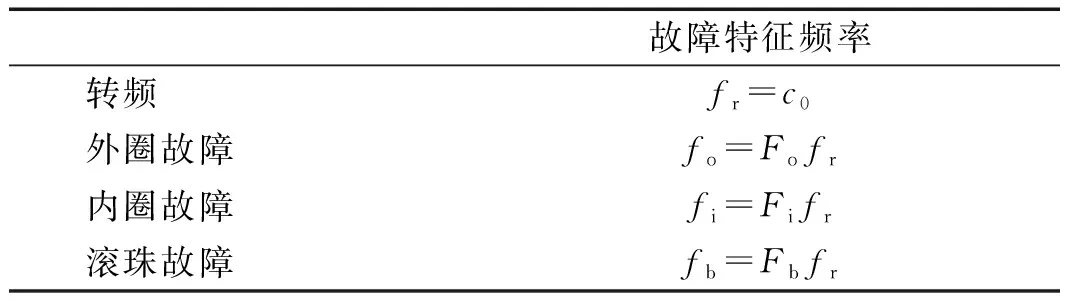
表1 广义特征指标计算Tab.1 Generalized feature calculation
1.3 量化诊断模型建立
由广义解调算法可知信号x(t)的时频分布是一条由f(t)确定的曲线。而MTFCE算法可从时频图中提取出f(t)。因此可以不通过解调变换直接从时频图中获取解调后的f0,再由f0进行故障诊断。
由MTFCE从时频图中提取出ISRF和IFCFs曲线,截取平滑段对其进行多项式拟合得到方程如下所示
yISRF=a0+a1t+a2t2+…+antn
(13)
yIFCF(k)=bk0+bk1t+bk2t2+…+bkntn
(14)
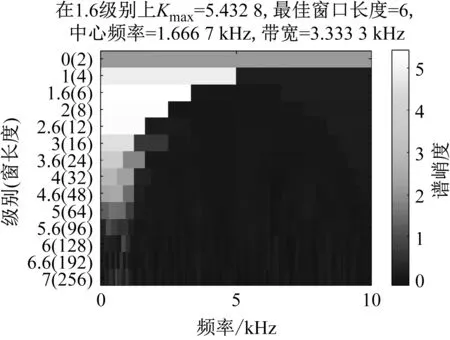
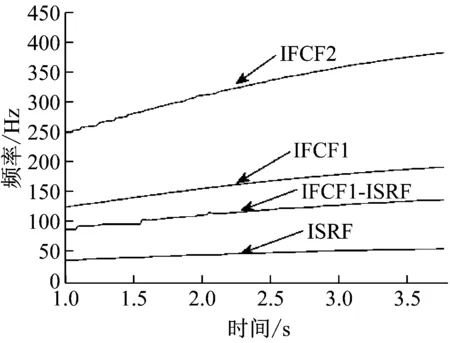
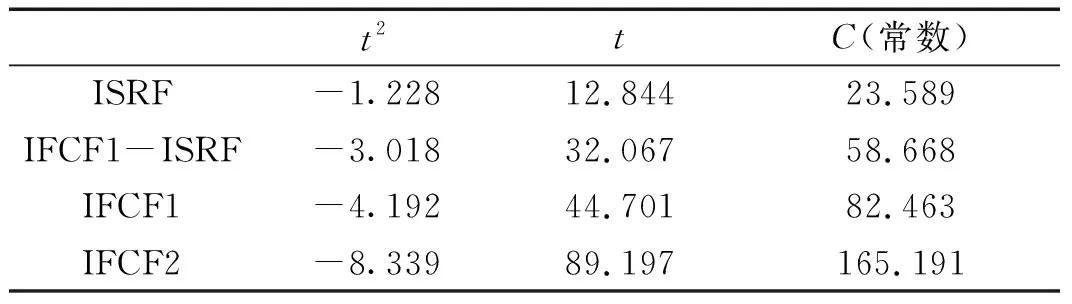
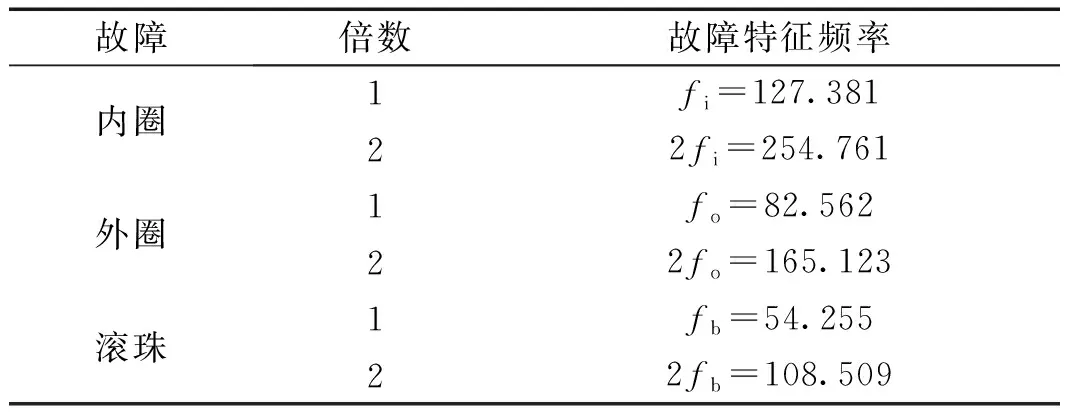
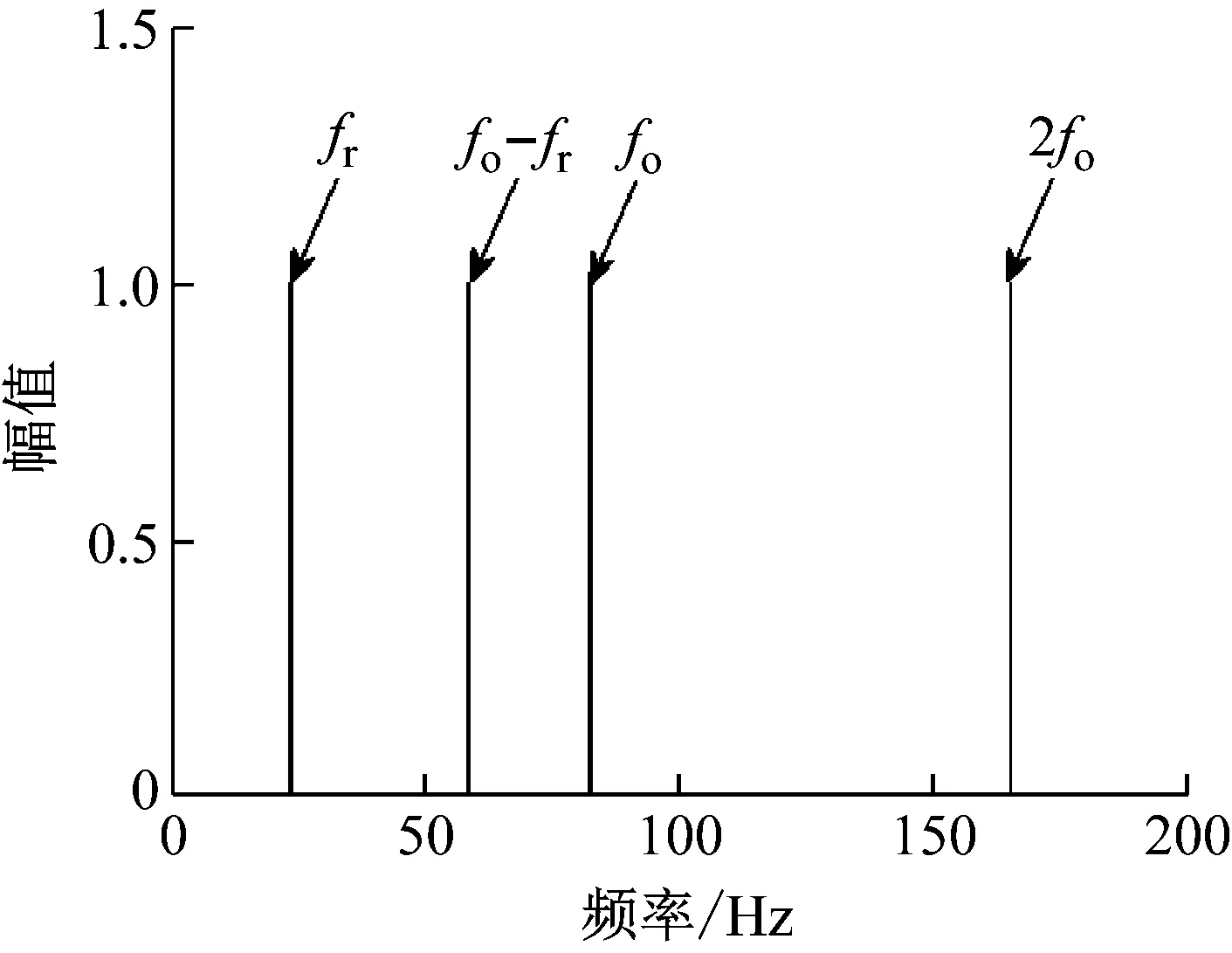
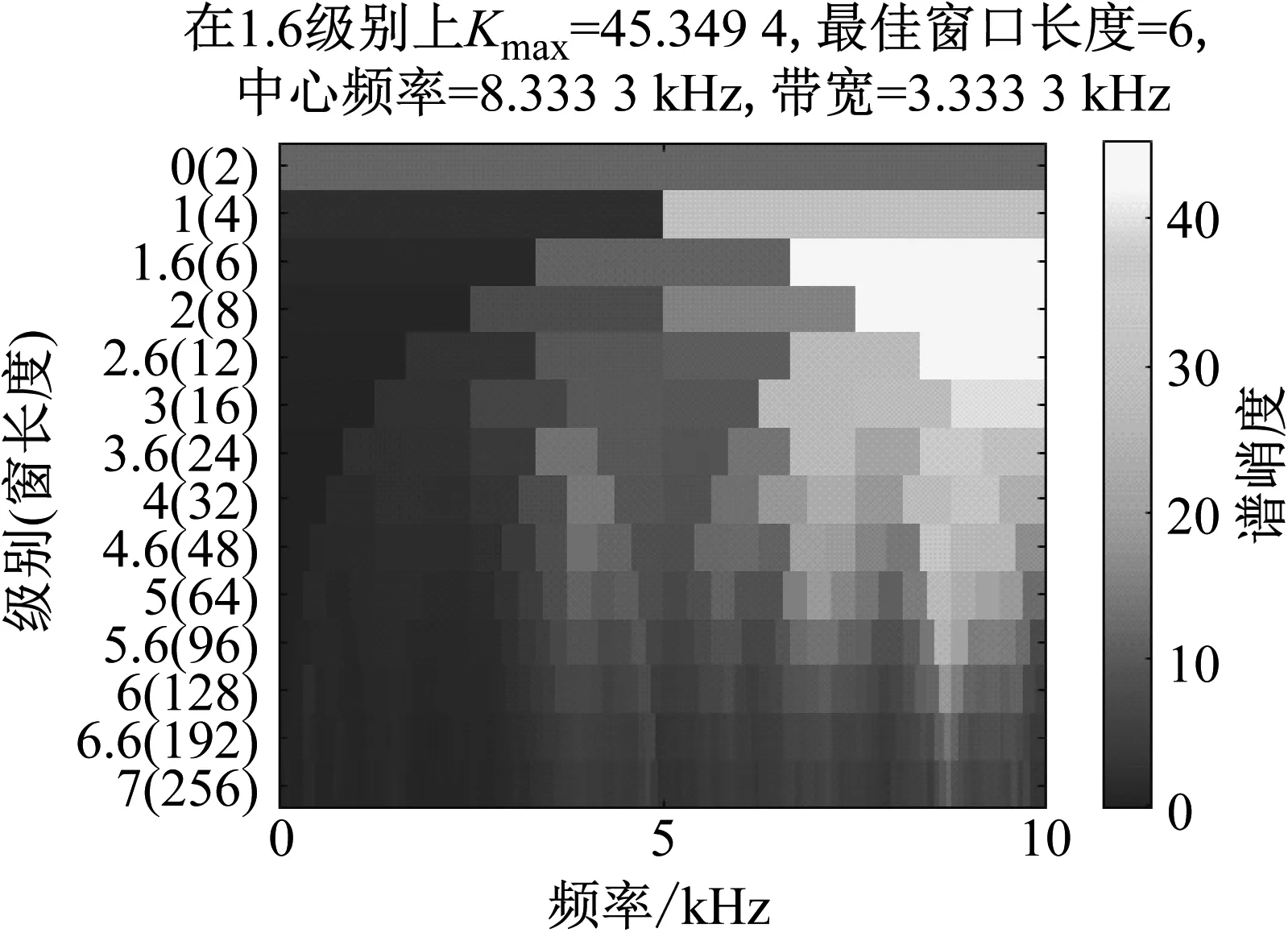
n=1,2,…,N且a0 由于故障特征频率趋势线在包络信号的时频图中表现为具有特定分布规律的曲线。MTFCE可以从时频图中直接提取出转频曲线。再经由多项式拟合获取转频方程,不需要额外安装转速计获取转速信息。拟合转频yISRF和预设转频y吻合时则表示该方法估计转频的有效性。 由于时频分辨率的限制,MTFCE提取的能够完整表征故障特征的曲线一般为3~4条。假设提取曲线为ISRF和IFCF1和IFCF2。结合表1计算故障广义特征频率,可构建量化诊断模型如图1所示。 图1 量化诊断模型Fig.1 Quantitative diagnostic model 将b10,b20与假设故障广义特征对比确定故障类型。为了方便故障诊断以及算法对比,绘制以bl0为频率的固定幅值频谱图结合量化诊断模型来进行故障诊断。 基于上述分析,本文提出一种基于多时频曲线提取广义特征的变转速轴承故障诊断方法。该方法流程图如图2所示。具体算法步骤如下所示: 图2 故障诊断方法流程图Fig.2 Flow chart of fault diagnosis method (1) 利用快速谱峭度算法计算最优带通滤波参数,并对原始振动信号进行滤波。 (2) 对滤波后的共振带信号进行短时傅里叶变换,并采用多时频曲线提取算法提取IFCFs和ISRF。 (3) 截取平滑曲线拟合IFCFs和ISRF曲线的多项式方程,再由拟合后的ISRF曲线参数结合表1计算广义特征。 (4) 由拟合后的IFCFs曲线参数绘制固定初始值频谱图,再结合图1量化诊断模型进行故障诊断。 为验证提出算法有效性,构造了升速条件下轴承故障仿真信号[21]。 xb(t)={1+A′(t)sin[2πf(t)·t]}· μ(t-tm) (15) 式中:A′(t) 为转频的瞬时幅值;f(t)为轴承转频;N为故障信号的冲击个数;Am为第m个故障冲击幅值;β为轴承衰减系数;ωr为故障的共振频率;μ(t)为单位阶跃函数;tm为第m个故障冲击发生时刻。其计算公式如下所示 (16) 其中τ为滚珠滑移引起的轴承故障冲击间隔误差,其取值通常为0.01~0.02。仿真信号具体参数如表2所示。 表2 故障轴承仿真信号参数Tab.2 Parameters of simulated faulty bearing signal 根据上述仿真模型得到的故障轴承振动信号如图3所示,对仿真信号进行快速谱峭度滤波得到共振带信号,滤波参数由图4的中心频率和带宽确定。然后利用短时傅立叶变换得到共振带信号的包络时频图如图5所示。可以从时频图中得到清晰的IFCFs和ISRF,而且可以发现初始阶段,转频较小时,故障特征的相关故障冲击幅值被噪声淹没。 图3 故障滚动轴承仿真信号Fig.3 Faulty rolling bearing simulation signal 图4 仿真信号Kurtogram图Fig.4 Kurtogram of simulated signal 图5 仿真信号包络时频图Fig.5 Envelope time-frequency diagram of simulated signal 利用多时频曲线提取方法提取ISRF和IFCFs曲线,截取平滑的T-F (time-frequency)曲线如图6所示,图中存在ISRF以及IFCFs以及IFCF1与ISRF的耦合曲线。对T-F曲线进行多项式拟合,拟合后的曲线参数如表3所示。从表中看出提取出的转频曲线的拟合方程f0=-1.228t2+12.884+23.589与预设的转频曲线的拟合方程基本一致。 图6 仿真信号截取的T-F曲线Fig.6 T-F curve after intercepting of simulated signal 表3 拟合曲线参数Tab.3 Parameters of the fitted curve 假设内圈故障系数Fi=5.4,外圈故障系数Fo=3.5,滚珠故障系数Fb=2.3。利用广义解调理论结合表1计算的仿真信号的广义特征指标如表4所示。由拟合曲线参数绘制固定幅值的初始值频谱图如图7所示,图中外圈故障特征频率fo及其谐波2fo被有效提取,可以确定轴承存在外圈故障。 表4 仿真信号广义特征指标计算Tab.4 Calculation of generalized features of simulated signals 图7 仿真信号固定幅值的频谱图Fig.7 Spectrogram of the simulated signal with fixed amplitude 为了验证本文所提方法的有效性,利用迭代广义解调算法,根据故障系数所确定的相位函数对信号循环进行解调变换。所得频谱图如图8所示。图中可以看出,频率峰值与轴承外圈故障特征频率吻合,但从圈出的椭圆部分可知,迭代广义解调算法存在频谱混叠现象,会造成故障误诊。本文方法相对于迭代广义解调算法表现更丰富故障相关信息,例如转频和转频与故障特征的耦合。体现了基于多时频曲线提取广义特征的变转速轴承故障诊断方法的有效性和优越性。 图8 迭代广义解调频谱图Fig.8 Spectrogram of iterative generalized demodulation 利用加拿大渥太华大学采集到的变转速滚动轴承的振动信号对算法的有效性进行进一步的验证。采用型号为MFS-PK5M的机械故障模拟器所采集的变转速工况下轴承数据进行验证,该数据采集频率为200 000 Hz,采集时间10 s,测试轴承的相关参数如表5所示,试验平台如图9所示,实例振动信号如图10所示。 表5 滚动轴承参数Tab.5 Rolling bearing parameters 图9 试验平台Fig.9 Test set-up 图10 实例振动信号Fig.10 Real faulty bearing signal 由滚动轴承参数可以计算出,内圈故障系数Fi=5.43,外圈故障系数Fo=3.57,滚珠故障系数Fb=2.32。利用快速谱峭度滤波算法对振动信号滤波得到共振带信号,滤波参数由图11的中心频率和带宽确定。对共振带信号的包络信号进行短时傅立叶变换得到时频图如图12所示。 图11 实例信号Kurtogram图Fig.11 Kurtogram of example signal 图12 实例信号包络时频图Fig.12 Envelope time-frequency diagram of example signal 利用MTFCE提取时频曲线,图13是截取平滑段以后的T-F曲线,对曲线进行多项式拟合。拟合后的数据如表6所示,转频方程为1.500t+12.568。由于该数据集提供了转速信息。图14显示了转频对比,从图中可以看出拟合后的转频曲线与实际测量转频误差很小,而从时频图中提取的转频与测量转频相差很大。 图13 实例信号截取以后的T-F曲线Fig.13 T-F curve after interception of example signal 表6 拟合曲线参数Tab.6 Parameters of the fitted curve 图14 转频对比图Fig.14 RPM comparison chart 由拟合后的ISRF和IFCFs绘制固定幅值的频谱图如图15所示。再根据表1计算的实例信号的广义特征如表7所示。结合量化诊断模型可以确定故障类型为内圈故障。图16为迭代广义解调频谱图,可以看出低频部分由于频谱混叠导致会存在故障的误诊。 图15 实例信号固定幅值频谱图Fig.15 Spectrogram of fixed amplitude of example signal 图16 实例信号迭代广义解调频谱图Fig.16 Example signal spectrogram of IGD 针对低变转速下滚动轴承故障振动信号呈现时变非平稳性,被噪声干扰无法有效诊断的问题,提出一种基于多时频曲线提取广义特征的变转速滚动轴承故障诊断方法,通过仿真和实例分析验证了所提方法的有效性。得出了以下结论: (1) 相对于迭代广义解调算法,本文方法无需对信号进行后续的解调变换,避免了频谱混叠问题。 (2) 通过基于假设思想的广义特征计算和量化诊断模型的构建,所提方法可对变转速工况下滚动轴承故障特征进行提取,有效的实现了变转速滚动轴承故障诊断,且鲁棒性较高。 (3) 由于海森堡不确定原理,短时傅里叶变换不能同时得到高的时间分辨率和频率分辨率。而MTFCE从时频图中提取IFCFs和ISRF,时频分辨率越高提取效果越好。后续将会提高时频分辨率上做研究,进一步提高曲线提取的准确性。
2 故障诊断

3 仿真分析




4 实例分析
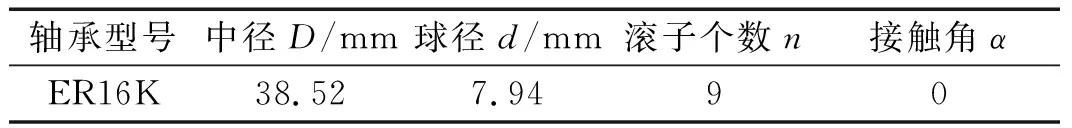








5 结 论
