采样方式对改进缩减基法在框架静力计算中的影响研究
2022-07-14李永红
李永红,梁 振
(中南林业科技大学土木工程学院,湖南 长沙 410004)
优化设计的时候,每次迭代设计参数发生变化,需要对模型重新分析。大规模问题,单次采用有限元法计算需花费较长的时间,影响优化设计的效率。近年来,缩减基法(reduced basis method,记作RBM)作为实时算法被用于各个领域。Milani R等[1]用缩减基法求解多参数线弹性问题。刘玉秋等[2]将缩减基法引入船舶制造结构。李永红等[3]将缩减基法用于蜂窝梁结构。马营利等[4]将缩减基法用于矿用车架。熊景林[5]将缩减基法用于冲压模具结构。缩减基法需要预先知道设计参数与线弹性算子的关系,李永红等[6]结合ANSYS,对缩减基法改进,得出单元线弹性算子与设计参数相关的表达式。
不同采样方式选取样本参数,构造减基矩阵,对改进缩减基法的结果有影响。本文按照三种分布方式选取样本参数,以平面框架结构为例比较不同样本参数计算结果的精度。
1 缩减基法理论及改进
1.1 缩减基法基本理论
结构进行求解时,设计参数发生变化,用有限元法计算得到的各点位移组成高维解空间。结构的静力平衡方程为:

式中 μ——设计参数;
K(μ)——结构刚度矩阵;
u(μ)——结构的结点位移向量;
F——结构荷载向量;
X——真实的高维解空间;结构总自由度为n。
选取N组样本参数,用有限元法求出对应结构的位移u(μ)。这N组位移构成减基矩阵Z,写成如下形式:Z=[u(μ1),u(μ2),…,u(μN)]。u(μi)(i=1,2,…,N)是线性无关的。当取新的设计参数μnew时,对应结构的位移可以看作是减基矩阵Z中各项的线性组合,即:

式中 a(μnew)——系数向量。
由能量最小原理并结合式(2),可得到:

其中KN(μnew)=ZTK(μnew)Z,FN=ZTF。
线弹性结构的刚度矩阵K(μ)可按照是否与设计参数相关分为两个部分,表示为下列形式:
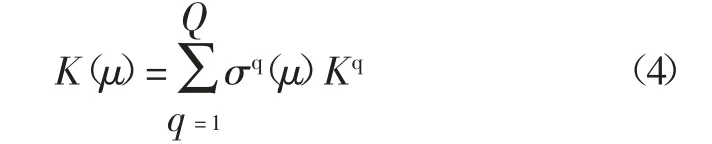
式中 σq(μ)——与设计参数相关的函数关系;
Kq——与设计参数无关的矩阵;
Q——刚度矩阵中设计参数能够分离的项数。
基于这种分解,缩减基法可以进行快速有效的实时计算。把式(4)代入式(3),令KqN=ZTKqZ(q=1,2,…,Q),可写成:
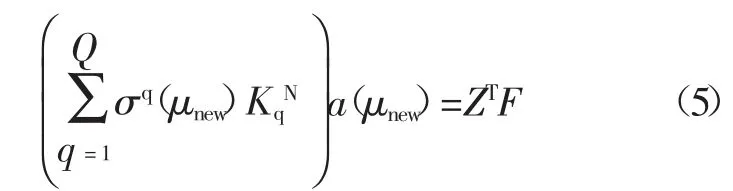
缩减基法将整个计算过程分为离线阶段和在线阶段。在离线阶段,将设计参数从刚度矩阵分离出来,选取样本参数,用有限元法计算得到的位移组成减基矩阵Z,预先算好KqN。在线阶段,取新设计参数时,算出σq(μnew),由式(5)求得a(μnew)。代入式(2),可得到缩减基法的位移解。式(5)的方程是N×N的,远小于式(1)的维度n×n。
1.2 改进缩减基法


各项都算出可组成KqN。取新设计参数时,结合缩减基法求解出位移解uGRBM(μnew)。
KqN计算过程如下:
1)分析所求结构的单元类型,用ANSYS建立该单元类型的简单模型。不断改变设计参数,找出线弹性算子与设计参数的联系。
2)选取多组设计参数,在ANSYS中提取对应结构的整体刚度矩阵。
3)用式(6)计算出与设计参数无关部分,集合得到KqN。
1.3 采样方式
结构选取何种采样方式构建样本空间,对改进缩减基法的计算结果有一定影响。分别用对数函数、均匀函数、切比雪夫函数采样构成样本空间来研究。对数函数采样:

均匀分布函数采样:

切比雪夫函数采样

式中 μi——结构的样本参数;
μmax——结构设计参数允许变化的最大值;
λ——设计参数下限μmin在函数中使用具有意义的比例系数。
2 数值算例
以多层框架结构为例,取其中的一榀平面框架结构进行分析。如图1所示,该模型有540个单元,521个节点,共有1 563个自由度。结构所受荷载如图2所示。

图1 平面框架结构的有限元模型

图2 结构荷载情况
本框架结构选取弹性模量E,梁单元的截面面积A两个设计参数。对这两个参数分别采取对数函数、均匀分布、切比雪夫函数采样,得到这三种分布方式对应的样本参数,构建成样本空间WN,用ANSYS软件计算对应结构位移,组成减基矩阵。选取新设计参数时,分别用有限元法和改进缩减基法计算输出,以有限元结果为精确解,如下式计算改进缩减基法的相对误差:

式中 S=FuFEM;S'=FuGRBM。
选取新设计参数时,采用改进缩减基法对结构进行计算。图3、图4对三种采样方式计算结果的误差进行比较,随着E、A样本数的增多,误差越来越小。
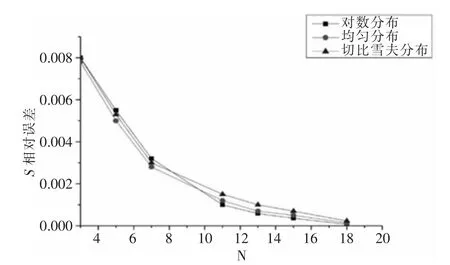
图3 E不同采样方式结果的相对误差

图4 A不同采样方式结果的相对误差
3 结论
本文采用三种函数采样方式构成样本空间,比较改进缩减基法结果的相对误差。分析同类型单元组成的简单结构,结合ANSYS提取刚度矩阵,得到分离关系。对缩减基法进行改进,计算出与设计参数无关的矩阵。以平面框架结构为例采用对数函数、均匀分布、切比雪夫函数方式选取样本参数,样本数较少时,均匀分布采样结果精度较高;随着样本数增多,对数分布与均匀分布采样结果精度趋于接近。
