CLO3D虚拟技术下黑白条纹的显瘦效果分析

2022-07-14王红歌孙晓婉

毛纺科技 2022年6期

王红歌，孙晓婉,2

(1.河南工程学院服装学院，河南郑州 451191； 2.浙江理工大学服装学院，浙江杭州 310018)

色彩、形状及点线面的多重组合使得图案设计百花齐放。条纹是最普遍的图案形式，既可理解为点的延续，又可解读为常规的线条，还可说成线排列重组后的面[1]。同时，条纹具有强烈的方向性、秩序感和节奏感，具备引导视线向条纹尽头延伸的能力，给人极大的使用与研究空间。早在1867年，德国著名科学家赫尔曼·赫尔姆霍兹在《生理光学手册》[2]中提出了赫尔姆霍茨正方形错觉图，即同一个正方形，由水平线条组成时看起来更高，由垂直线条组成时看起来更宽。Thompson和Mikellidou通过2D/3D界面下的2组实验，发现横条纹使女性的臀部显得更瘦，证实了赫尔姆霍兹正方形错觉对服装穿着的适用性[3-5]。然而Swami等[6]则质疑该实验设计的合理性，其通过研究得出相反结论，即穿着横条纹服饰时身材更显宽。针对上述研究分歧，Ashida等[7]发现，着装者的身材、服装评价者的特点及实验样本的呈现次序均会影响赫尔姆霍兹正方形错觉在服装中的应用。而赵伶俐等[8]的研究发现线条粗细以及线条间距等都会影响赫尔姆霍兹正方形错觉效应在服装上的表现。韩楚悦[9]则认为横线条与竖线条的视错觉带来的心理效应各有千秋。冯程程[10]得出条纹中线条变化与人体曲线及动态变化相关关系。虽然关于条纹的显瘦效果已展开了诸多研究，但各方意见仍不尽一致，有待更深入的探索。

本文排除色彩、款式等干扰要素，以黑白条纹(方向、宽度)、人体体型、基础面料为着力点，基于比例优化的H型连衣裙，运用CLO3D虚拟技术，开展条纹连衣裙显瘦效果的验证与探究，并总结相应规律，以期为条纹面料开发及连衣裙的生产设计提供一些参考。

1 实验设计

1.1 连衣裙款式设计

连衣裙是女性夏季穿着的主要服装品类，其款式变化各异，视觉呈现千差万别。为契合研究目的，排除款式干扰，确定以无分割、无腰线连衣裙为实施载体，连衣裙廓形为H型，肩点距离、裙长、腰线上下区域长度等吻合黄金矩形思维。连衣裙款式设计思路及呈现效果见图1。

图1 连衣裙款式设计思路及呈现效果Fig.1 Design thoughts & effects of dress style. (a)Front;(b)Back

1.2 条纹面料设计

1.2.1 基础面料选择

选择夏季连衣裙常用的纯棉、亚麻/棉混纺、纯羊毛、桑蚕丝、涤纶及棉/粘胶混纺(编号依次为M1～M6)作为基础面料，面料信息如表1所示。

表1 面料信息Tab.1 Information for fabrics

1.2.2 条纹方案确定

黑白条纹方案涵盖方向、宽度、间距等要素。以市场调研为手段，兼顾实验结论的有效性与覆盖度，确定预方案为：横、竖向，黑白纹等宽，条纹宽度范围为0.5～9.0 cm，递增间距为0.5 cm。常见的黑白条纹如图2所示。条纹方案确定流程如图3所示。

图2 常见的黑白条纹Fig.2 Common black and white stripes

图3 条纹方案确立流程Fig.3 Process chart for stripe plan making

根据预方案，参照GB/T 1335—2008《服装号型》中的女性中间体(160/84A)为对象构建试衣环节所需的虚拟人体，以纯棉面料为载体，以条纹方向(2水平)、宽度(18水平)为研究对象开展预实验。获取36个实验样本，借助问卷星平台面向在校女大学生收集评价数据，共获取有效评价120个。分析发现，87.5%的评价人员认为条纹宽度大于6 cm时，条纹宽度占比过大，与人体宽度的协调性差，使得连衣裙的美感不佳。根据上述结论调整条纹方案为：横、竖向(编号D1、D2)；条纹宽度范围为0.5～6.0 cm，递增间距为0.5 cm(编号依次为S1～S12)；黑白条纹纹等宽。

1.3 人体建模

服饰穿着者的体型对条纹的视觉效果会产生影响[7]。参照GB/T 1335.2—2008《服装号型女子》，成年女性人体根据胸腰差可分为Y、A、B、C 4种体型。考虑推广性，本文选取国标中各体型的中间体，即160/84A、160/84Y、160/88B、160/88C，进行人体建模(编号依次为N1～N4)。各体型人体控制部位尺寸如表2所示。

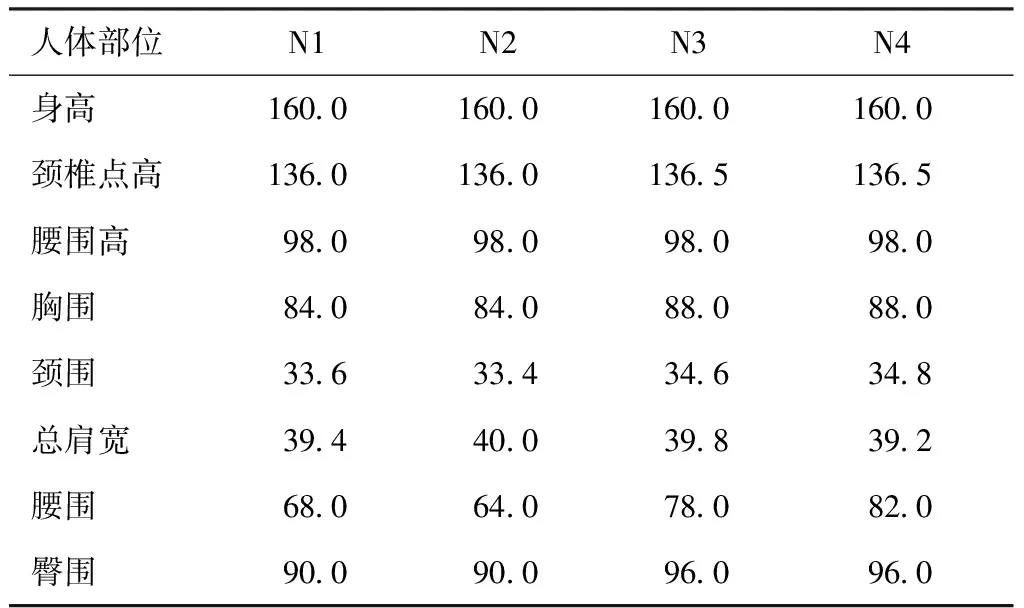
表2 各体型人体控制部位尺寸Tab.2 The human body size for the main part cm

参照表2数据，利用CLO3D软件的虚拟模特功能对人体控制部位进行数据编辑，完成人体建模。图4所示为N2的建模结果。

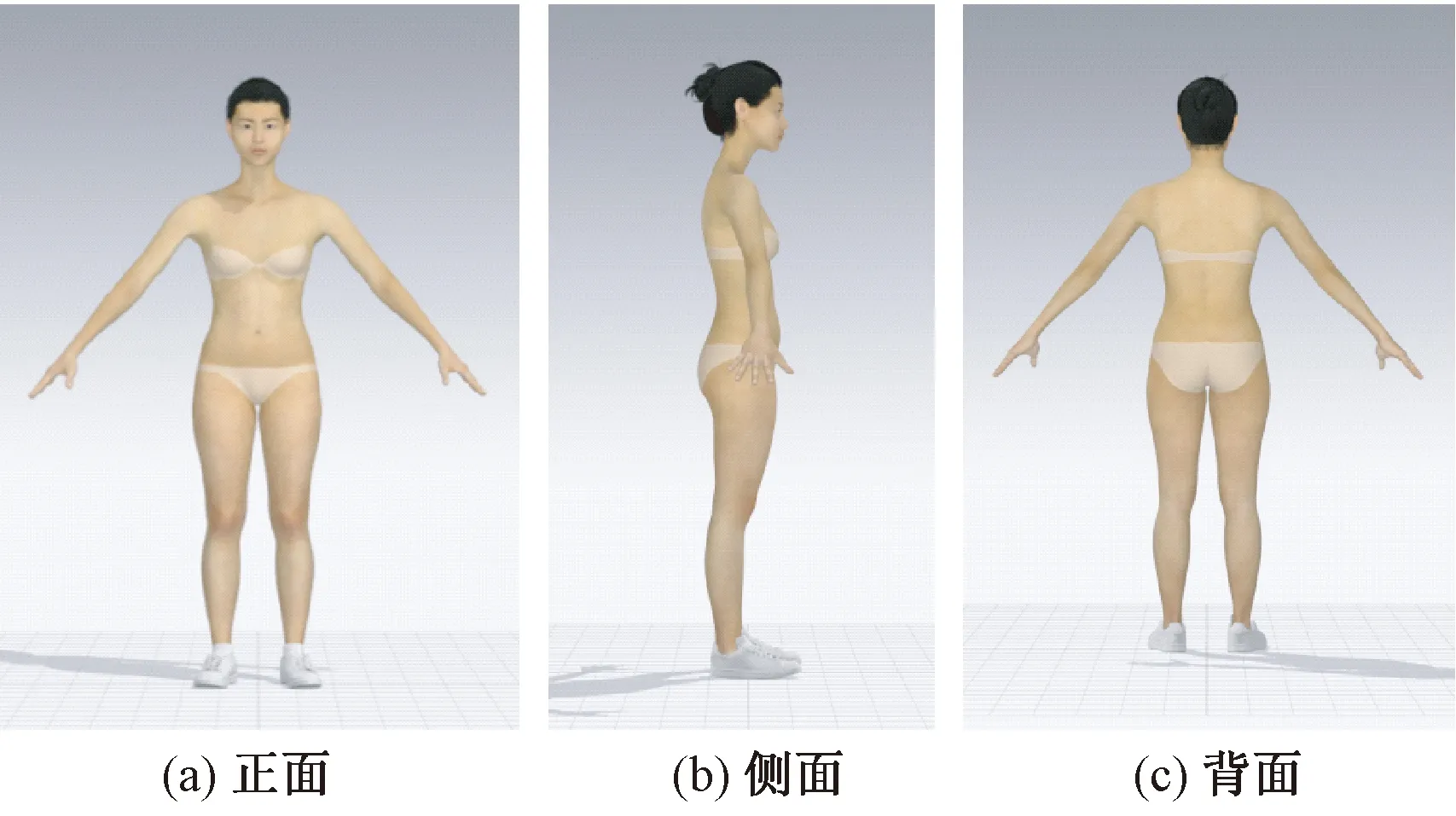
图4 N2的建模结果Fig.4 Modeling results for N2. (a) Front; (b) Side; (c) Back

1.4 实验过程

运用CLO3D虚拟技术软件进人体建模、条纹面料设计、二维纸样调整及三维虚拟展示以获取实验样本。采用语义差异法以现场评分的形式对实验样本进行评分。评分采用5分赋值法，即“显瘦度弱”(1分)、“显瘦度较弱”(2分)、“显瘦度一般”(3分)、“显瘦度较强”(4分)、“显瘦度强”(5分)。参照GB/T 10220—2012《感官分析方法学总论》，感官检验的优选评价员取20人以上即可[11-12]。为保证评价结果的准确性及可靠性，评价员均为大学服装专业三、四年级学生，人数36人。其中，男性9人(25%)，女性27人(75%)。

实验样本的呈现次序会对条纹视觉效果产生影响[7]，所以本文实验样本出现的次序保持一致，即以人体体型、条纹宽度为考察依据，形成48组评价，每组评价含12个样本。实验样本展示如图5所示，图示为样本M1D1S3N2和M1D2S3N2。考虑实验样本量大、参与人员视觉刺激疲劳等因素，评价实验分阶段展开，期间实验环境、参与对象等保持一致。

图5 实验样本展示Fig.5 Displaying of experimental samples. (a) Sample M1D1S3N2; (b) Sample M1D2S3N2

评价要求及流程如下：

①场地要求：设置4个实验条件一致的评价场地，每个场地安排9张桌椅，沿墙放置，间距1 m以上。

②时间要求：单次评价时长为15～20 min，完成6组评价样本。评价员可根据自身情况对时长、评价量略做调整。间隔时间大于5 min。计时工作由工作人员负责。

③分组及其他要求：评价员被平分为4组，每组固定1个评价场地，每人分配1张桌椅、48组评价样本(次序一致)及评价表。

④评价流程：首先，第1次评价前，工作人员围绕评价目的，评价样本的编码规则、呈现次序，评价流程等对评价员进行培训、答疑；其次，评价员按1#～48#的顺序依次观看每组中的12张连衣裙照片，依据感官刺激情况填写评分表；再次，单次评价结束，评价员与工作人员交接完毕，在规定场所休息，等待下次评价；最后，每次评价结束，工作人员梳理已完成的评价样本和评分表，核查是否有漏填、歧义之处，若有需重新评价。

2 结果与分析

2.1 评价数据的整体概述

评价实验中，36个评价员对576个实验样本逐一打分，即生成576×36个原始评分。利用SPSS软件对评分进行预处理，即原始评分的异常值检测、描述性统计分析等。将36名评价员对同一实验样本的评分进行均值处理，则每个实验样本对应1个显瘦度评分，由此获得文件Ⅰ，包含576个数据样本，据此可展开进一步统计分析。条纹连衣裙显瘦度整体评价如表3所示。

表3 条纹连衣裙显瘦度整体评价Tab.3 Overall evaluation of thin effect of striped dress

由表3可知，评价员对连衣裙显瘦度的平均态度为“显瘦度一般”(3分)，但最高评分为4.75分，则接近“显瘦度强”(5分)，对应样本M4D1S1N1(桑蚕丝、横条纹、宽度0.5 cm、160/84A)和M5D1S1N3(涤纶、横条纹、宽度0.5 cm、160/88B)。同时，最低评分为1.86分，接近“显瘦度较弱”(2分)，对应样本M1D2S12N1(纯棉、竖条纹、宽度6 cm、160/84A)和M6D2S12N3(棉/粘胶、竖条纹、宽度6 cm、160/88B)。此外，显瘦度评分的偏度系数为0.63，大于0，表明显瘦度评分呈正偏态分布；峰度系数为-0.71，小于0，表明两侧极端评分较多。进一步分析发现，此类评分主要来自竖条纹实验样本。

为更清晰地呈现评价员对576个实验样本显瘦情况的态度，以显瘦度区间为依据对文件Ⅰ进行分类，共7类。各区间样本数统计结果如图6所示。

图6 各区间样本数统计结果Fig.6 Statistic results of sample number for each range

由图6可知，显瘦度在“一般”(3分)及以上的数据样本有240个，占比41.7%。此240个数据样本组成文件Ⅱ。

对比文件Ⅰ、Ⅱ发现，条纹宽度对显瘦度影响很大，且条纹宽度为4～6 cm的实验样本，其显瘦度评分均小于3分。同时，条纹方向对显瘦度影响也较大，文件Ⅰ中，显瘦度评分小于3分的竖条纹实验样本有205个，占比35.6%，而横条纹实验样本有131个，占比22.7%。文件Ⅱ中，横条纹实验样本有157个，占比65.4%，且显瘦度评分均值为4.01分，而竖条纹样本的显瘦度评分均值为3.25分，表明横条纹显瘦度更优，有悖于“竖条纹更显瘦”的说法，与赫尔姆霍兹正方形错觉则一致。此外，基础面料、人体体型对显瘦度的影响规律尚不清晰，需进一步分析。

2.2 面料质地与显瘦度的统计分析

为减少分析误差，6种基础面料对显瘦度的影响分析依据文件Ⅱ展开。面料与显瘦度的描述性统计如表4所示。

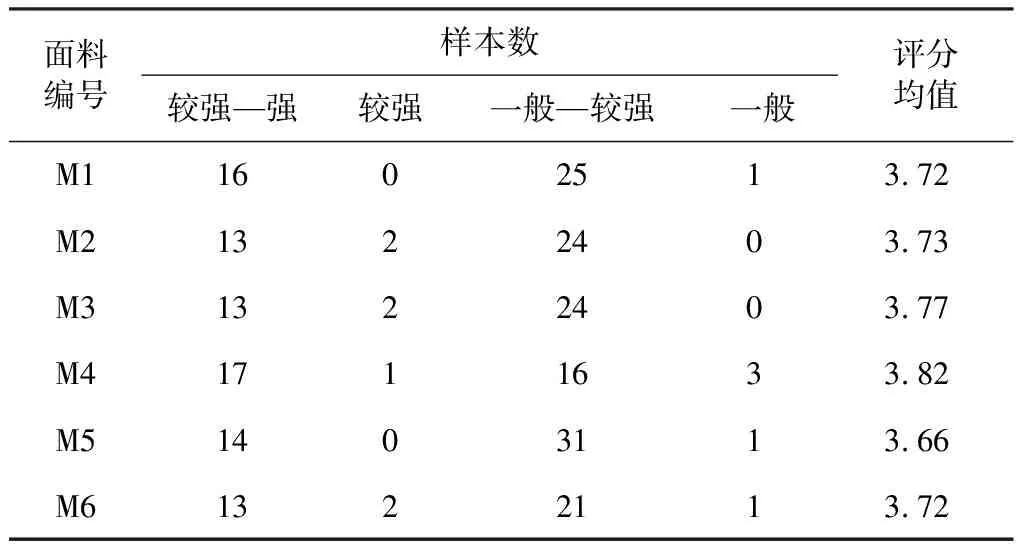
表4 面料与显瘦度的描述性统计Tab.4 Descriptive statistics of fabric and thin effect

由表4可知，6种基础面料的显瘦度评分均值都在“一般—较强”区间内，数值差异不大。其中，M4(桑蚕丝)显瘦度最佳，M5(涤纶)显瘦度最弱。为深入探究不同面料对显瘦度的影响，基于文件Ⅱ，以基础面料为变量，遴选29个数据样本，组成文件Ⅲ，以此开展Shapiro-Wilk正态性检验和配对t检验。配对t检验中，M5为对照组，其他为实验组。Shapiro-Wilk正态性检验统计如表5所示，配对相关性统计(面料)如表6所示，配对t检验(面料)如表7所示。

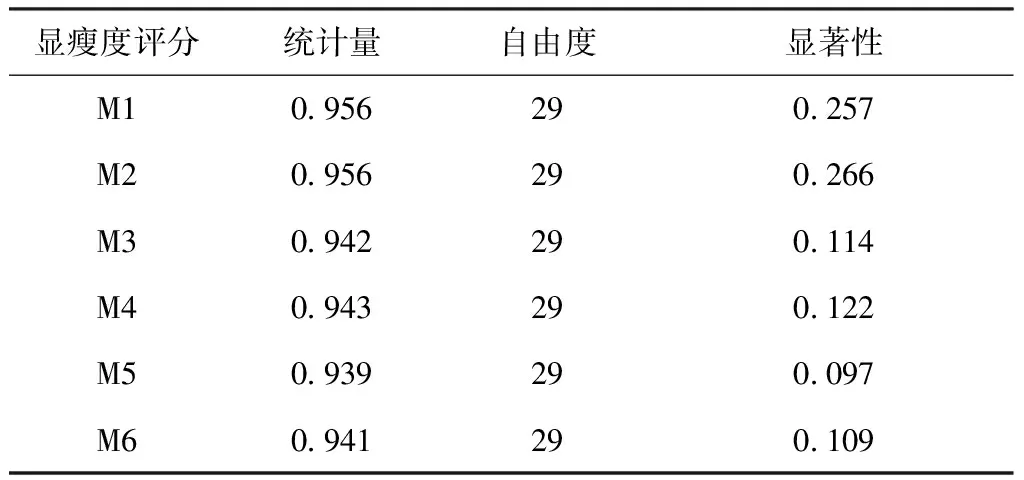
表5 Shapiro-Wilk正态性检验统计Tab.5 Shapiro-Wilk normality test statistics

表6 配对相关性统计(面料)Tab.6 Paired correlation statistics(material)

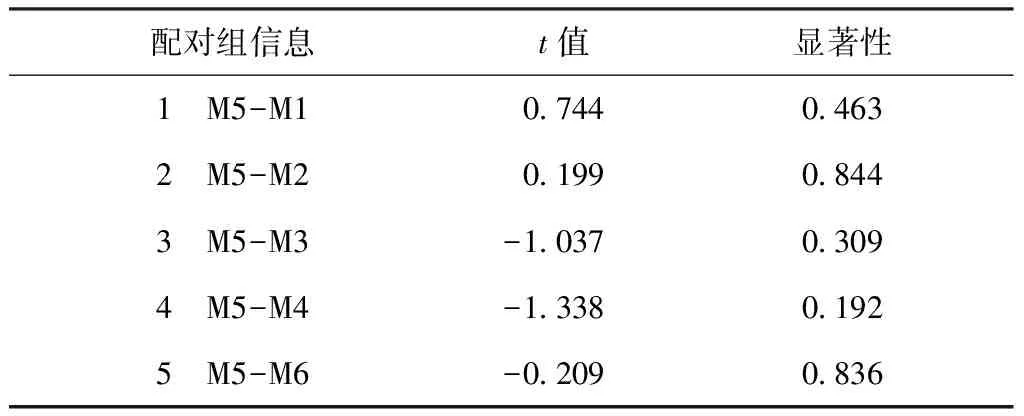
表7 配对t检验(面料)Tab.7 Paired t-test(material)

由表5～7可知，Shapiro-Wilk检验中，显著性均大于0.05，说明文件Ⅲ中6种面料的显瘦度评分均服从正态分布。配对t检验中，各对组的显著性均大于0.05，表明显瘦度评价中M5与其他面料的差异性不具备统计学意义，且在配对相关性分析中，M5与其他面料的显瘦度评分呈正相关(显著性均小于0.05)，虽相关性不够强，但表征趋势一致。由此得出结论：基础面料对显瘦度的影响不大。原因有二，其一，基础面料上绘制黑白条纹后，视线集中点发生了转移，更关注条纹；其二，虚拟场景下，面料属性参数设置受限，呈现的虚拟展示效果与实际着装效果存在差异。

2.3 条纹方向与显瘦程度的统计分析

以文件Ⅱ中条纹宽度在0.5～3.0 cm的横条纹数据样本为对象进行统计分析，分析结果如表8所示。可知，条纹宽度在0.5～3.0 cm的横条纹实验样本有144个，而显瘦度评分在4分及以上的实验样本有90个，表明横条纹对人体体型、条纹宽度的约束小于竖条纹。此外，显瘦度评分均值随着条纹宽度的增加而依次减小，呈反比关系。

表8 条纹宽度和方向与显瘦度的描述性统计Tab.8 Descriptive statistics of stripe width and direction with thin effect

同上，对文件Ⅱ中的竖条纹数据样本分析发现，竖条纹显瘦度整体弱于横条纹，但融合人体体型要素开展多视角分析，可得出竖条纹连衣裙在胖体(N3/N4)上的显瘦度优于标准体(N1)和瘦体(N2)。此外，从文件Ⅰ遴选条纹宽度为4～6 cm的数据样本，组成文件Ⅳ，对其展开统计分析发现，竖条纹的显瘦度优于横条纹，一定程度说明竖条纹显瘦度与条纹排列的密度、位置有关系。人体宽度协调的宽条纹更易牵引视线延伸，即竖条纹的位置设置合适即可修饰人体。由此可知，条纹方向对显瘦度有影响，但影响不具备绝对性，需综合评判。

2.4 人体体型与显瘦程度的统计分析

基于文件Ⅰ，以人体体型要素为变量，分遴选144个数据样本，组成文件Ⅴ，以此展开配对t检验。其中，N1(160/84A)为对照组，N2、N3、N4为实验组，基本统计信息如表9所示，配对相关性统计(人体)如表10所示，配对t检验(人体)如表11所示。

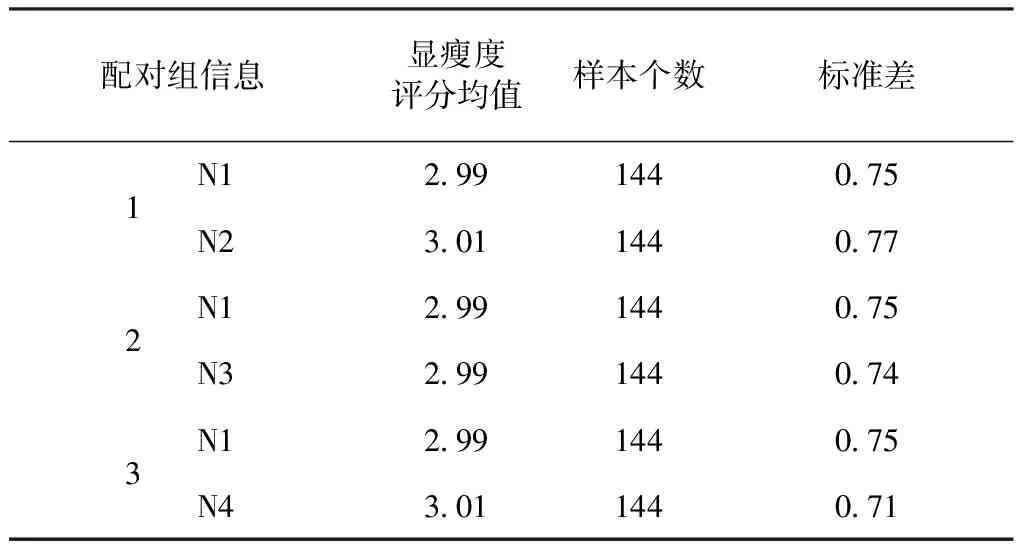
表9 基本统计信息Tab.9 Basic statistic information

表10 配对相关性统计(人体)Tab.10 Paired correlation statistics(human body)

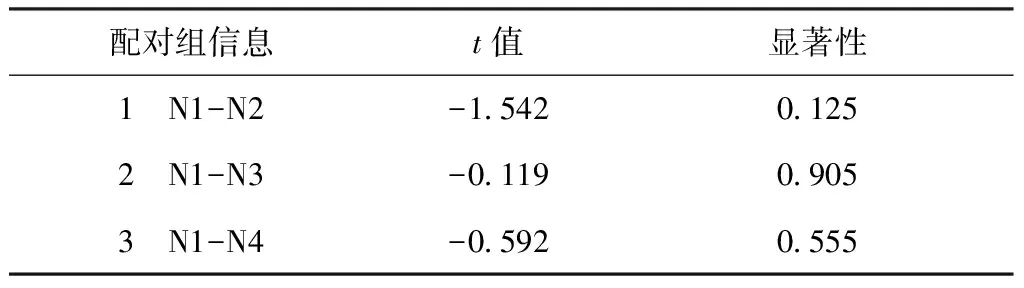
表11 配对t检验(人体)Tab.11 Paired t-test(human body)

由表9～11可知，不同体型的条纹显瘦度均为“一般”(3分)，且N1与其他体型的显瘦度评分呈正相关，相关系数趋于1。配对t检验中，各配对组的显著性均大于0.05，表明显瘦度评价中N1与其他体型的差异性不具备统计学意义，即体型变化对显瘦度的影响不显著，但结合2.3节中的分析结论，即人体体型对竖条纹的显瘦度有影响，由此表明人体体型变化对条纹显瘦度的影响不具备独立性，需综合其他关联要素进行综合分析。各体型显瘦度较好的实验样本如表12所示。

表12 各体型显瘦度好的实验样本Tab.12 Experimental samples showing good thin effect

由表12可知，条纹宽度为S1(0.5 cm)，条纹方向为横向时，人体体型对条纹显瘦度的影响微乎其微且无规律可循。此外，各体型显瘦度较好的实验样本中，M3(纯毛)、M4(蚕桑丝)均出现3次，频次最高；M5(涤纶)、M1(纯棉)次之，M2(亚麻/棉)、M6(棉/粘胶)最弱。这与2.2节中的相关分析结论趋于一致。

2.5 条纹宽度与显瘦程度的统计分析

综合2.1～2.4节中的分析结论，基于文件Ⅰ，以条纹方向为变量，拆分2组，组成文件Ⅵ(含288个横条纹数据样本)和文件Ⅶ(含288个竖条纹数据样本)。基于文件Ⅰ开展要素交叉分析。条纹宽度与显瘦度的交叉分析如图7所示。

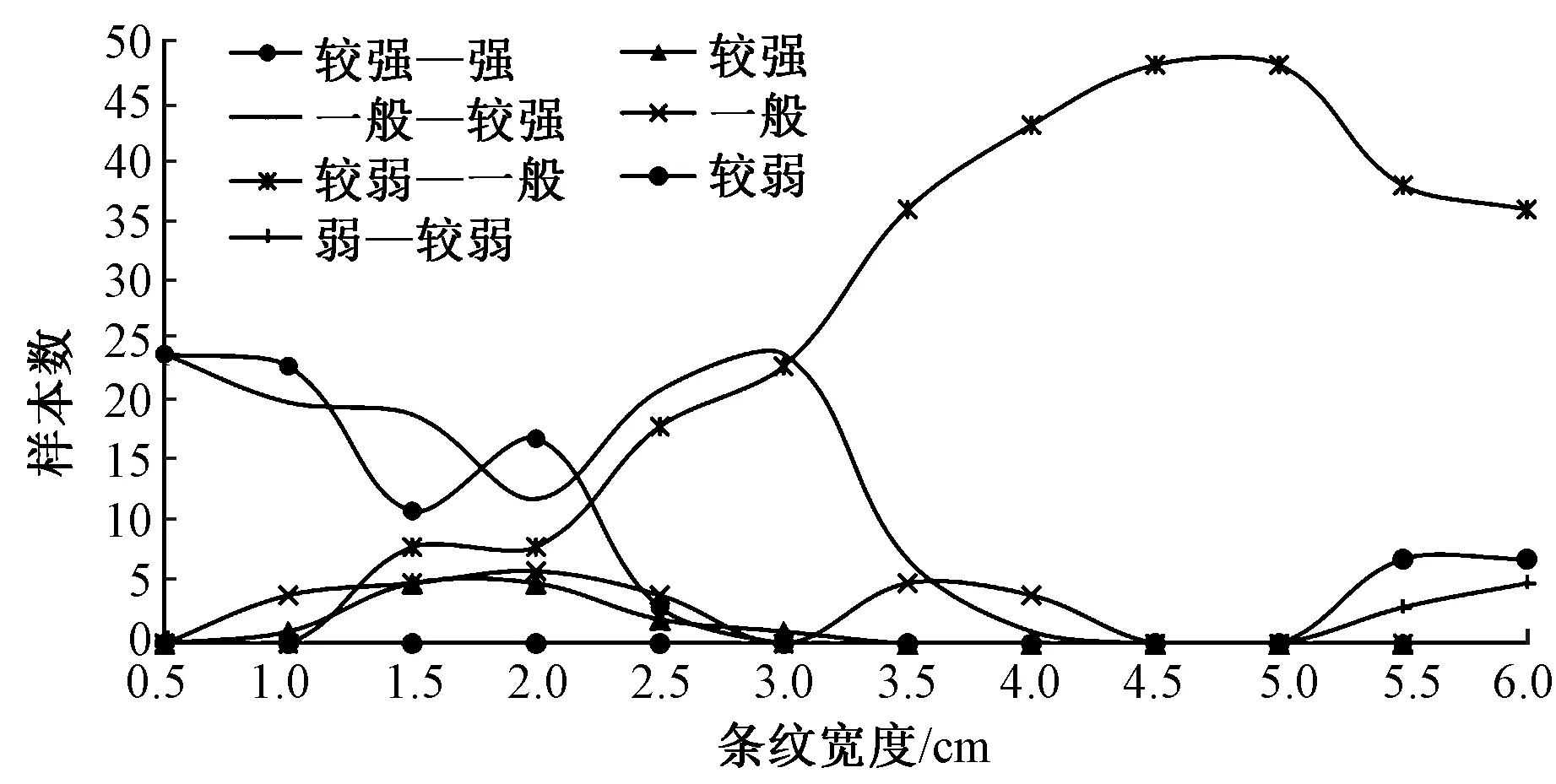
图7 条纹宽度与显瘦度的交叉分析Fig.7 Cross analysis of stripe width and showing thin effect

由图7可知，条纹宽度为3.5～6.0 cm时，显瘦度基本在“较弱—一般”区间，与2.1节中的分析结论趋于一致，即条纹宽度对显瘦度的影响显著，但宽度大于3 cm时，对显瘦度的影响减弱或消失。为进一步研究条纹宽度与显瘦度的量化关系，并考察条纹宽度范围、条纹方向对量化关系的干扰情况，本文对文件Ⅰ、文件Ⅱ、文件Ⅵ和文件Ⅶ分别展开统计分析。相关性统计如表13所示。

表13 相关性统计Tab.13 Pearson correlation statistics

由表13可知，4个数据源的统计分析中，相关系数的显著性sig均为0，小于0.01，说明二者存在相关性，因相关系数小于0，即为负相关。基于文件Ⅱ得到的相关系数为-0.265，表明二者的相关性弱，其他数据源得到的相关系数均趋向-1，为强相关关系，且文件Ⅵ、文件Ⅶ得到的相关系数更佳。由此可知，以条纹方向、显瘦度区间为变量对文件Ⅰ进行拆分，会对原有数据结构、特征等产生影响。为此，本文基于文件Ⅵ、文件Ⅶ展开线性回归分析，结果见式(1)(2)所示。

yⅥ=-0.45xⅥ+4.79

(1)

式中：yⅥ代表显瘦度评分，分；xⅥ代表条纹宽度，cm。

式(1)模型的拟合度判定系数R2=0.899，回归系数的显著性值为0.000，方差检验的显著性值为0.000。

yⅦ=-0.25xⅦ+3.50

(2)

式中：yⅦ代表显瘦度评分，分；xⅦ代表条纹宽度，cm。

式(2)模型的拟合度判定系数R2=0.823，回归系数的显著性值为0.000，方差检验的显著性值为0.000。

由式(1)(2)可知，条纹宽度为0.5～6.0 cm时，条纹宽度与显瘦度评分间的线性关系显著，且回归模型的拟合度较好。