含有三阶色散和自频移与自陡峭项的立方-五次非线性薛定谔方程的孤子解

练少鹏 李 威

(北京化工大学 数理学院,北京 100029)

引 言

非线性薛定谔方程广泛应用于非线性量子场论、等离子体物理学、光子学、流体力学、半导体电子学、生物物理学、经济物理学等诸多领域,其表达式为

它是数学物理学中最重要的模型之一,在Bose-Einstein凝聚中也被称为Gross-Pitaevskii(GP)方程。该方程存在孤立子解。由于孤立子在运动过程中有保持形状不变的性质,可应用于光纤通信领域,故寻找该系统的孤立子解具有重要意义。

在非线性光学中,系统(1)描述了皮秒光脉冲在单模光纤中的传播[1],这里u(x,t)表示复包络振幅,x和t分别表示空间和时间变量,β2表示群速度色散系数,α1表示自相位调制参数。但是,当超短脉冲接近50 fs,甚至低于10fs,或光场频率接近光纤材料的谐振频率时,单模光纤中高能超短脉冲传输的理论和实验结果表明,系统(1)失效,这时必须考虑对系统(1)增加由拉曼散射引发的附加项[2-3]。

文献[4]对系统(1)增加了五次非线性项、自陡峭项和自频移项

并且运用试探函数法得到孤子解。文献[5-8]对系统(1)增加了三阶色散项、自陡峭项和自频移项

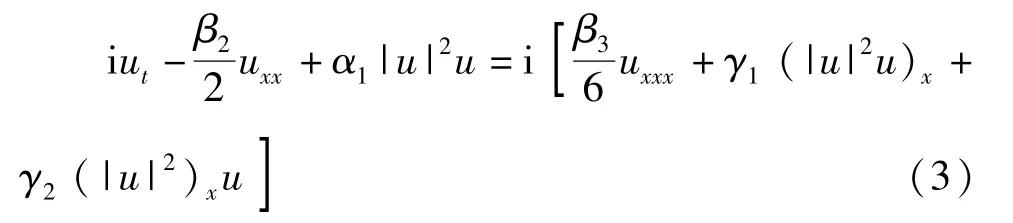
同时运用了Sine-Gordon方程法、F-展开法、Exp-展开法等方法求解。

本文综合所有影响因素,寻找系统

的精确解。由于系统(4)中出现了五次非线性项α2|u|4u和三阶色散项uxxx的并存现象,导致一些常用的求解方法不适用,为此我们选择合适的变量代换,并选用3种辅助函数展开法—Riccati方程-展开法、Riccati方程-倒数展开法和Exp-展开法来寻求方程(4)的解析解。

1 行波变换

对方程(4)作行波变换:u(x,t)=φ(ξ)ei灼,其中ξ=v0t-vx,灼=ω0t-ωx,可得

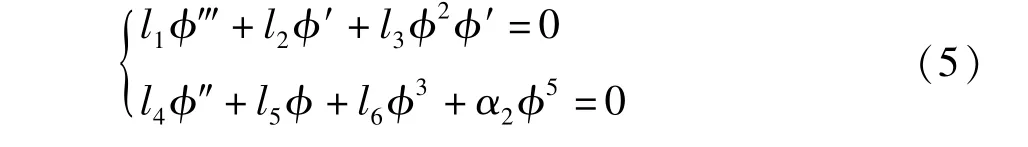
对方程(5)第一个式子积分,并选取首次积分常数为0,通过代入消去φ的三次项,可得

式中,A=l1l6-l3l4/3,B=l2l6-l3l5/3,C=-α2l3/3。

下面对方程(6)使用辅助函数展开法,求解出函数φ的表达式,从而给出方程(4)的解析解。

2 辅助函数展开法

设方程(6)的解具有如下展开结构

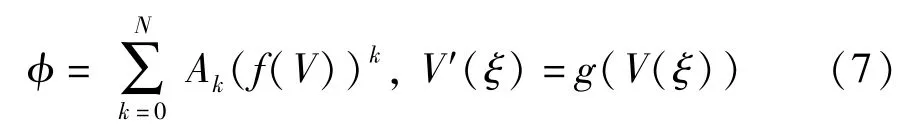
式中,Ak为待定常数,N为平衡整数。先将式(7)代入到方程(6)中,再利用齐次平衡原理确定N,最后通过求解方程(7)给出系统(4)的解。为此选择代换φ=Q1/4,则方程(6)化简成

2.1 Riccati方程-展开法

选取f(V)=V和g(V)=S2V2+S1V+S0,则式(7)变为

式中,S0、S1和S2为常数且S2≠0。易知Riccati方程的解如下。

当s＞0时,

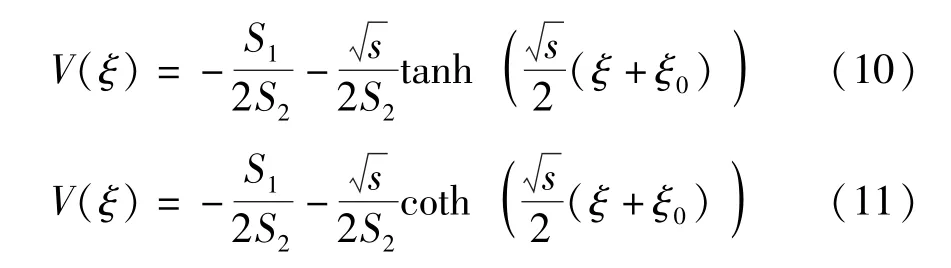
当s＜0时,

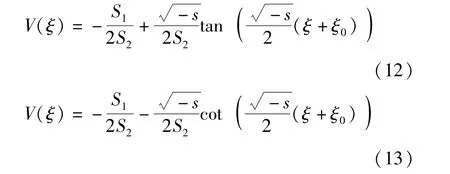
当s=0时,

将方程(9)代入方程(8)后,通过比较Q3、(Q′)2和QQ″关于V的最高次幂,可得N=2以及关于V的一元高次方程。由于V≠0,于是选取Vk(k=0,1,…,6)的系数为0,可得如下方程组

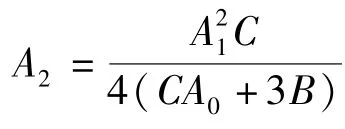
当AB＜0时,

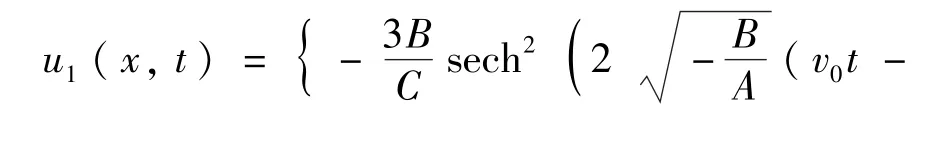
当AB＞0时,

图1 亮-孤立波u1,激波u2和周期波u3、u4的三维波形图Fig.1 Three-dimensional waveforms of the bright-soliton wave u1,shock wave u2 and periodic waves u3,u4

2.2 Riccati方程-倒数展开法

选取f(V)=1/V和g(V)=S2V2+S1V+S0,则式(7)变为

将方程(19)代入方程(8)后,通过比较Q3、(Q′)2和QQ″关于1/V(ξ)的最高次幂,可得N=2以及关于1/V(ξ)的高次方程。由于V≠0,故选取(1/V(ξ))k(k=0,1,…,6)的系数为0,可得类似的系数方程组。借助Maple求解,可知在A0满足条件A(A0C+3B)＜0时,S0、S1、S2、A2分别为

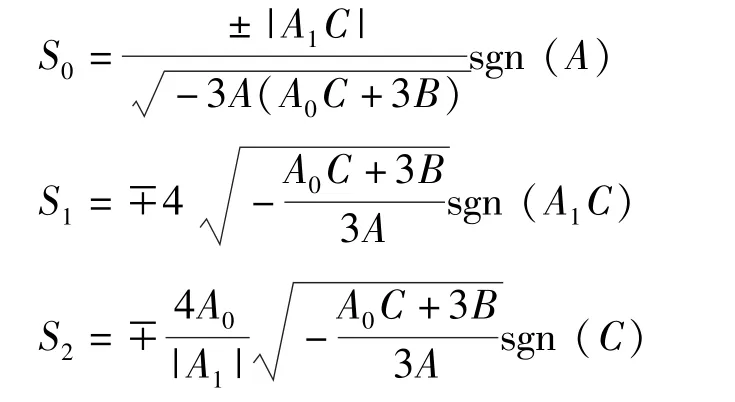
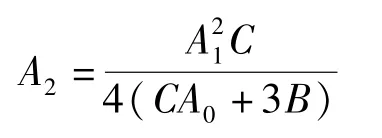
其中A1为任意非0常数,s=-16B/A。利用式(10)～(13)可得方程(4)的解如下。

当AB＜0时,

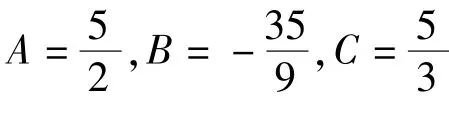
图2 亮-孤立波u5,激波u6和周期波u7、u8的三维波形图Fig.2 Three-dimensional waveforms of the bright-soliton u5,shock wave u6 and periodic waves u7,u8

2.3 Exp-展开法

选取f(V)=exp(-V)和g(V)=exp(-V)+R1exp(V)+R0,则式(7)变为

式中R0和R1均为常数。易知上述关于V(ξ)的微分方程的解如下。

当μ＞0,R1≠0时,

当μ＜0,R1≠0时,

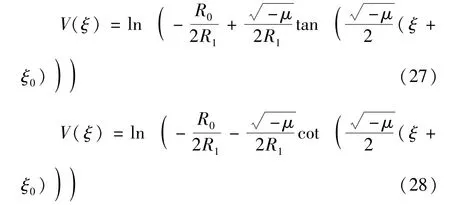
当μ=0,R1≠0,R0≠0时,

将方程(24)代入方程(8)后,通过比较Q3、(Q′)2和QQ″关于exp(-V(ξ))的最高次幂,可得N=2以及关于exp(-V(ξ))的高次方程。由于exp(-V(ξ))≠0,故选取exp(-kV(ξ))(k=0,1,…,6)的系数为0,可得如下方程组。

借助Maple求解出A0、A2、R0、R1分别为

当AB＜0时,

当AB＞0时,

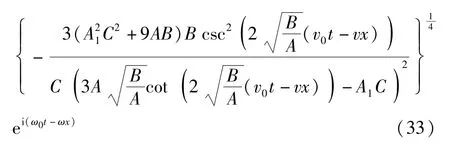
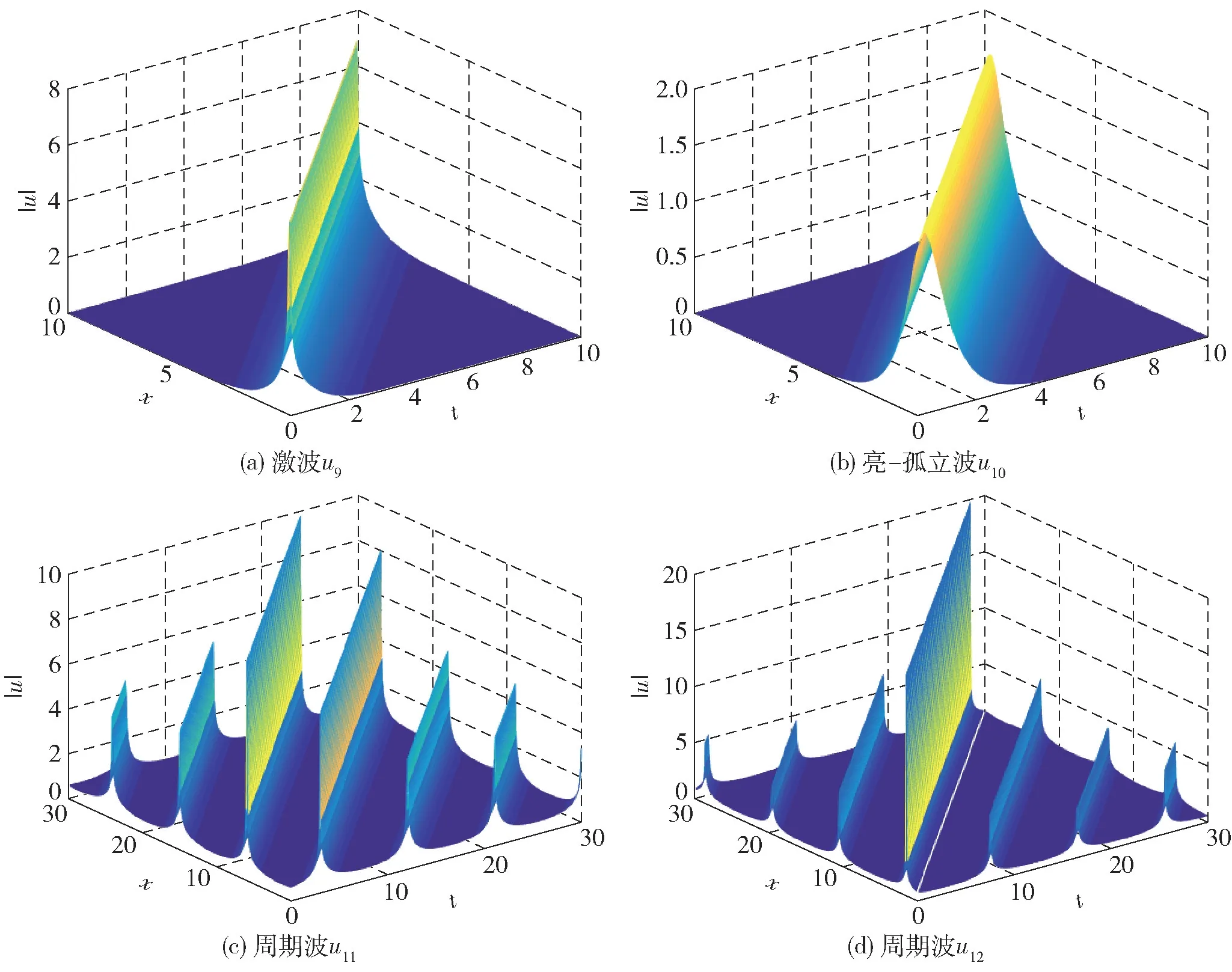
图3 激波u9,亮-孤立波u10和周期波u11、u12的三维波形图Fig.3 Three-dimensional waveforms of the shock wave u9,bright-soliton wave u10 and periodic waves u11,u12

通过比较可以发现以上3种方法存在内在关联性:

1)Riccati方程-展开法的解表达最简,不含自由参数,倒数展开法的解有2个待定参数A0、A1转化为非0自由参数,Exp-展开法中有1个待定参数A1转化为自由参数;

2)倒数展开法中限定参数S0=1,所得解即为Exp-展开法求得的解;

3)Exp-展开法限定参数A1=0,所得解即为Riccati方程-展开法求得的解。

3 结束语

本文结合文献[4-8]对系统(1)进行改进得到新方程(4)。该方程通过行波变换化简为二阶常微分方程(6)。由于高次项φ5和二阶导项φ″在辅助函数法代入过程中关于V的次数变化幅度不同,导致无法选出合适的N来达到次数平衡。为此,引入变量代换φ=Q1/4,将方程(6)转化为方程(8),运用多种辅助函数展开法—Riccati方程-展开法、Riccati方程-倒数展开法、Exp-展开法,求解出几种类型的解析解,如亮-孤立波、激波和周期波,并且发现这3种方法求得的解存在一定的交集。