地铁隧道整体道床轨道脱空对车轨振动的影响
2022-07-14蒋吉清章亦然董北北陈春来
蒋吉清,章亦然,董北北,陈春来,魏 纲,丁 亮
(1.浙大城市学院土木工程系,浙江杭州 310015;2.浙江大学建筑工程学院,浙江杭州 310058)
引言
地铁可有效缓解城市交通拥堵,但也带来了噪声、振动及一系列自身安全问题[1]。受到周边工程建设、水文地质条件和列车长期循环荷载等因素影响,部分地铁隧道区段道床与下部结构间出现了空洞甚至脱空,对地铁隧道的正常运营产生了不利影响,严重路段甚至会危及行车安全[2-4]。在成都地铁1号线三期工程中,全线共发现约1 000处道床与管片剥离[5]。因此,研究整体道床轨道局部脱空对地铁车轨振动的影响具有重要的工程意义。
国内外已有不少学者研究整体道床轨道局部脱空对车轨振动的影响。在地铁轨道方面,彭华等[6]利用ABAQUS有限元软件建立了轨道-道床-衬砌三维空间耦合模型,分析了道床局部脱空下的变形,并用实测数据对破坏特征进行分析;季存建[7]通过数值模拟研究了道床脱空在3种不同施工工法下的力学响应,并对道床脱空进行了评价;在高速铁路方面,田秀淑等[8]利用LS-DYNA建立了轨道板-砂浆层-支承层-路基有限元模型,分析了道床在不同脱空尺寸下系统的频谱和速度时程曲线特性,并提出了识别砂浆层缺陷的参数;李培刚等[9]采用有限元方法,建立了列车-轨道-桥梁垂向非线性耦合振动模型,分析了不同脱空区域尺寸条件下车轨动力响应。从现有文献来看,地铁隧道整体道床轨道局部脱空主要采用有限元模拟,缺乏较为系统的理论研究。
文中基于车辆-轨道耦合动力学理论[10-11],建立了地铁列车-整体道床轨道-隧道衬砌-地基二维垂向耦合模型,分别考虑了道床底部脱空以及道床、隧道底部同时脱空等不同情况,分析了不同脱空长度和车速下的车轨系统响应,并从中提取出对于局部脱空最为敏感的振动指标。
1 模型建立及方程求解
1.1 地铁整体道床车轨系统模型
图1所示为地铁列车-整体道床轨道-隧道衬砌-地基二维耦合模型。假设列车由2节车厢组成,每节车厢包括车体、转向架、轮对以及一系、二系悬挂系统,其中,车体、转向架和轮对均简化为刚体,一系和二系悬挂系统由弹簧-阻尼单元进行模拟,车体和转向架考虑竖向和点头位移,轮对只考虑竖向位移,共计10个自由度。钢轨采用两端简支的Euler梁[12]模拟,钢轨下方扣件采用离散的弹簧-阻尼单元模拟。整体道床和隧道衬砌分别采用两端简支的Timoshenko梁[13]进行模拟,两者之间采用离散的弹簧-阻尼单元相连,隧道衬砌周边的土体也采用离散的弹簧-阻尼单元模拟。

图1 地铁整体道床车轨系统Fig.1 Metro train-monolithic track bed system
1.2 车轨系统振动方程
基于达朗贝尔原理,建立列车动力方程如下:

式中:M、C和K分别为列车的质量矩阵、阻尼矩阵和刚度矩阵;v为列车的位移向量,共有20个自由度,包括前后2节车体的竖向位移vc1、vc2和点头位移φc1、φc2,4个转向架的竖向位移vb,i(i=1,…,4)和点头位移φb,i(i=1,…,4),8个轮对竖向位移Zw,i(i=1,…,8);上标“··”和“·”分别表示列车位移关于时间的二阶导数和一阶导数;F为列车各部分所受的外力矩阵。
钢轨由一根两端简支的Euler梁模拟,其控制方程为:

式中:Er为钢轨弹性模量;Ir为钢轨截面惯性矩;vr(x,t)为钢轨在x位置处t时刻的竖向位移;ρr为钢轨密度;Ar为钢轨截面面积;Prs,j为第j个扣件的扣件力;xrs,j为第j个扣件的位置;nrs为扣件数量;xw,i(t)为第i轮对在t时刻所在位置;P(xw,i(t))为第i轮对在t时刻的轮轨接触力;δ为狄拉克函数。轮轨接触力和扣件力的表达式如式(3)~式(5)所示。

式中:Krs和Crs分别为扣件刚度和阻尼;Kwr为轮轨接触刚度;zw,i(t)为第i轮对在t时刻的竖向位移;vh(x,t)为整体道床在x位置处t时刻的竖向位移。
整体道床和隧道衬砌分别模拟为两端简支的Timoshenko梁,其控制方程表达式如式(6)~式(9)所示。

式中:κh、κt分别为道床和衬砌剪切系数;Ah、At分别为道床和衬砌横截面积;Gh、Gt分别为道床和衬砌剪切模量;φh(x,t)、φt(x,t)分别为道床和衬砌在x位置处t时刻的转角位移;vh(x,t)、vt(x,t)分别为道床和衬砌在x位置处t时刻的竖向位移;ρh、ρt分别为道床和衬砌密度;Eh、Et分别为道床和衬砌弹性模量;Ih、It分别为道床和衬砌截面惯性矩;Fh(x,t)为道床所受的扣件反力和衬砌支承反力;Ft(x,t)为道床下传力和地基土反力;Fh(x,t)、Ft(x,t)公式分别如(10)~式(11)所示。

式中:nhs为道床和衬砌之间离散弹簧阻尼单元个数;nts为衬砌和土体之间离散弹簧阻尼单元个数;xhs,j为道床和衬砌之间第j个弹簧阻尼单元位置;xrs,j为衬砌和土体之间第j个弹簧阻尼单元位置;Phs,i(t)、Pts,j(t)分别为在t时刻道床与衬砌间第i个弹簧阻尼单元力和衬砌与土体间第j个弹簧阻尼单元力,公式分别如(12)~(13)所示。

式中:Chs、Cts分别为道床与衬砌间离散单元阻尼;Khs、Kts分别为衬砌和土体间离散单元刚度。
采用模态叠加法进行正交分解,分别得到钢轨、道床和衬砌的常微分振动方程,将其与式(1)联立,即可得到列车-整体道床-衬砌-地基耦合振动方程,最后利用Newmark算法进行数值计算。
1.3 局部脱空模型
在地铁隧道长期运营过程中,道床与衬砌之间、衬砌与地基之间都有可能发生局部脱空情况,影响地铁安全运营。图2为整体道床轨道局部脱空区段,整体道床与衬砌、衬砌与地基之间离散弹簧-阻尼单元的间距设为0.1 m,并按从左到右依序编号。在脱空区段,上下层结构之间发生局部脱离。为简化起见,本文假设脱空区域道床和衬砌之间的离散弹簧-阻尼单元刚度系数、阻尼系数都设置为0,且不考虑非线性接触;当考虑衬砌与地基之间的局部脱空时,也类似处理。

图2 地铁整体道床轨道局部脱空区段Fig.2 Local disengagement section of metro monolithic track bed
2 模型验证及数值分析
2.1 模型验证
为验证模型及计算方法的正确性,将文中结果跟文献[14]有限元软件的计算结果进行对比。参照文献[14]的算例设置,假设钢轨长度取为420 m,车速300 km/h,脱空长度2.5 m(距离左侧端点206.4 m~208.9 m区段),将整体道床模型修改为两端自由的Timoshenko梁,其它模型参数如表1所示。
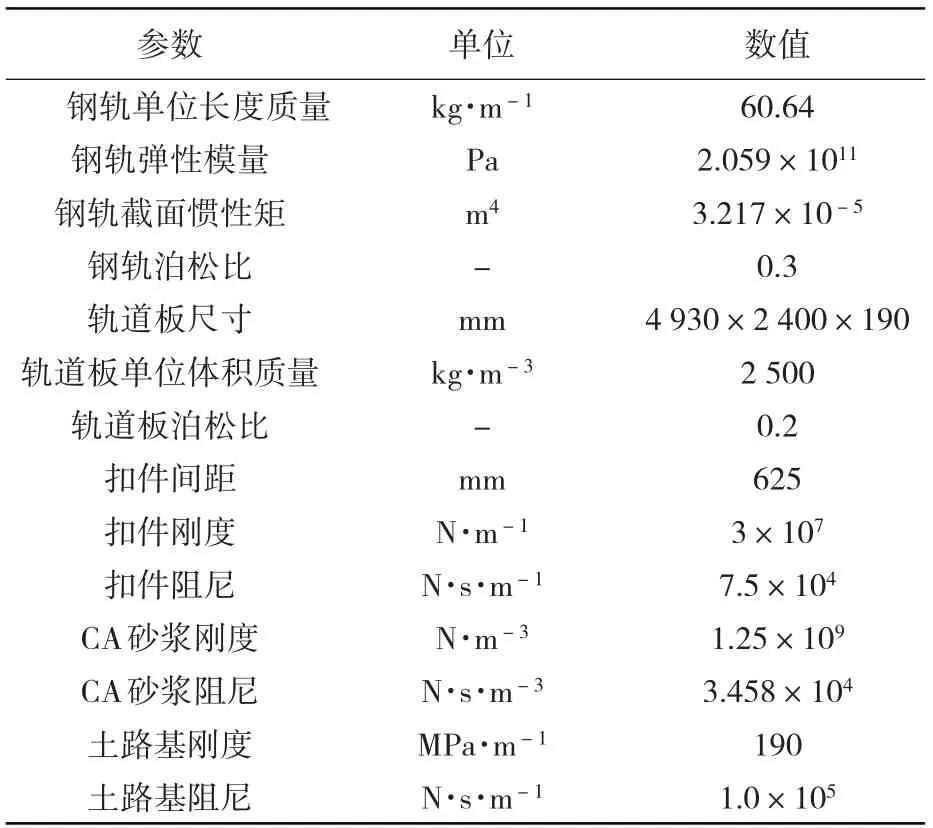
表1 文献[14]参数取值Table 1 Parameter values of literature[14]
图3为本文计算得到的钢轨位移时程曲线图。经对比发现,本文与文献[14]的钢轨垂向位移时程曲线规律一致,在脱空区段钢轨位移均有突变。本文与文献[14]的钢轨位移振动幅值分别为0.45 mm和0.53 mm,误差为15%。考虑到文献[14]的列车参数以及轮轨接触刚度等部分计算参数没有列明,且本文结果跟文献[14]结果整体变化趋势上基本吻合,因此可以认为本文计算方法正确,计算结果具有可参考性。

图3 钢轨位移时程曲线Fig.3 Time history curve of rail displacement
2.2 局部脱空的数值分析
在下面的算例中,列车及轨道的计算参数取值参考文献[15],其中,钢轨、道床及衬砌的长度取为325 m,扣件类型为DTVI2-1型,扣件间隔为0.625 m,即,在计算范围内共520个扣件。整体道床和衬砌之间的弹簧-阻尼单元参数值参考文献[16],即弹簧刚度值取为100 MN·m-1,阻尼值取为20 kN·s·m-1。此外,参考《桩基工程手册》中桩周土反力系数计算方法并采用Novak法确定地基参数,即弹簧刚度值取为10 MN·m-1,阻尼值取为375 kN·s·m-1,地铁列车运行速度取为72 km/h。轨道系统计算参数见表2。

表2 轨道系统计算参数Table 2 Track system calculation parameters
假设整体道床及衬砌之间局部脱空,衬砌与地基之间保持完好接触,脱空长度为2.0 m,脱空区域为编号1616到1635的弹簧-阻尼单元区段(参见图2标示,距离左端点161.5 m~163.5 m),分别计算脱空前后地铁车轨系统的振动响应。
2.2.1 道床局部脱空的影响
图4为整体道床与衬砌之间局部脱空对地铁车轨振动的影响。由图4可见,当列车到达脱空区域(即距离左端点161.5 m~163.5 m,具体见图4标示)附近,相较于未脱空情况,地铁车轨系统各项动力响应都将显著增大,其中,首车车体竖向加速度幅值在脱空前后分别为4.10×10-5m/s2和5.76×10-4m/s2,增幅最为显著,达到了1 303.2%。首个转向架竖向加速度幅值分别为2.86×10-3m/s2和7.39×10-3m/s2,增大了159%。道床加速度幅值以及首轮对加速度幅值的增幅分别达到了63.8%和54%。
此外,由图4(a)可见,脱空情况下车体竖向加速度时程曲线有4个峰值点,分别对应着列车4个转向架的前轮对驶过脱空区域正上方时的车体动力响应。此外,当首车驶过脱空区域后,受第2辆车体振动的影响,首车位移和加速度仍有少量增幅。从影响区域来看,车体竖向加速度受脱空影响的范围较大,转向架竖向加速度、道床加速度和轮对加速度受脱空影响的范围较小。

图4 道床与衬砌间的局部脱空对车轨振动的影响Fig.4 The effect of local disengagement between the monolithic track bed and the lining on the vibration of the train-track system
图5是地铁车速在72 km/h情况下,不同脱空长度对车体竖向加速度影响范围的大小。由图5可见,脱空长度与车体竖向加速度受影响的范围呈正相关,且随着脱空长度的增加,车体竖向加速度的影响范围曲线趋于平缓。

图5 脱空长度对车体竖向加速度的影响范围Fig.5 The influence range of the disengagement length on the vertical acceleration of the carriage
2.2.2 列车速度的影响
考虑地铁列车速度对整体道床局部脱空情况下车轨振动的影响,图6为列车速度取36 km/h、57 km/h、72 km/h、90 km/h和144 km/h情况下,地铁车轨动力响应随道床脱空长度的变化规律。

图6 列车速度及脱空长度对车轨振动幅值的影响Fig.6 The effect of train speed and disengaging length on the vibration amplitude of train-track system
由图6可见,车体竖向加速度、转向架竖向加速度、轮对加速度、道床加速度、钢轨位移和道床位移等振动幅值均随脱空长度的增大而增大。其中,车轨的竖向加速度振动幅值跟列车速度呈正相关,且随着车速的增大,脱空长度的变化对车轨振动的影响程度也显著增大,如图6(a)、(d)~(f)所示。钢轨位移、道床位移的幅值随车速的增大而减小,且在不同车速情况下,脱空长度对车轨振动的影响趋势差别不大,具体见图6(b)、6(c)。此外,由图6(e)、6(f)可知,在常见地铁列车速度情况下,即车速低于72 km/h时,脱空长度对轮对加速度幅值和道床加速度幅值的影响较小。
当整体道床脱空长度一定时,不同列车速度对于地铁车轨振动的受影响范围具有显著影响。以车体竖向加速度为例,当整体道床脱空长度取为2.0 m情况下,车体竖向加速度的受影响范围随着列车速度的增加而增加,二者近乎呈正比关系,具体如图7所示。

图7 车速对车体竖向加速度的影响范围Fig.7 Influence range of vehicle speed on carriage vertical acceleration
2.2.3 道床与衬砌同时脱空的影响
在地铁列车荷载、地面堆载、邻近工程施工等因素影响下,软土地区地铁隧道易发生不均匀沉降[17-18],造成隧道变形以及整体道床与衬砌之间的局部脱空,此外,隧道衬砌与土体之间也可能发生局部剥离。在下面的算例中,文中同时考虑了道床与衬砌、衬砌与地基之间的组合脱空情况,假设列车运行速度仍取为72 km/h,分别取4种不同的工况进行对比研究:(1)工况1,道床和衬砌间脱空1.2 m,衬砌和地基间脱空2.0 m;(2)工况2,道床和衬砌间脱空1.6 m,衬砌和地基间脱空2.0 m;(3)工况3,道床和衬砌间脱空2.0 m,衬砌和地基间脱空2.0 m;(4)工况4,道床和衬砌间脱空2.0 m,衬砌和地基间脱空1.2 m。
表3为4种工况下地铁车轨振动幅值的计算结果。由表3可知,相较工况1,工况2和工况3情况下的首车车体加速度、首个转向架加速度、轮对加速度和道床加速度幅值均明显增大,其中,车体加速度幅值分别增大了30.4%、70.3%,转向架加速度幅值分别增大22.8%、50.1%,轮对加速度幅值分别增大10.8%、23.6%,道床加速度幅值分别为12.6%、28.1%;而钢轨位移、道床位移、衬砌位移及衬砌加速度则变化较小。此外,由表3可知,工况3和工况4的各项振动响应幅值差别不大,由此可见,在组合脱空情况下,道床和衬砌之间的局部脱空对车轨振动的影响较为显著,而衬砌与地基之间的局部脱空对其影响较小。
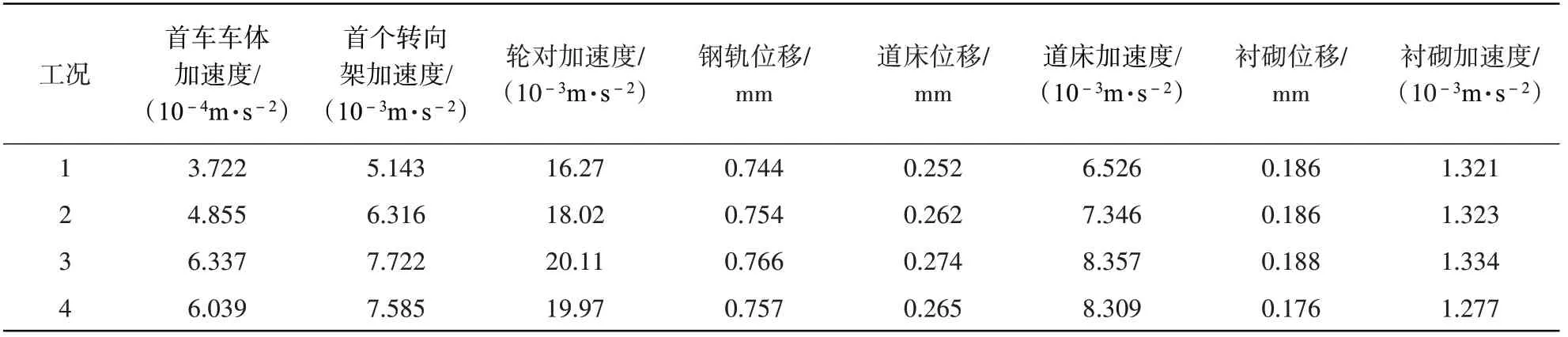
表3 四种工况下的车轨振动幅值Table 3 Train-track vibration amplitudes under four different cases
3 结语
本文基于车辆-轨道耦合动力学理论,建立了地铁列车-整体道床轨道-隧道衬砌-地基垂向耦合模型,考虑了地铁隧道底部和整体道床底部的局部脱空情况,并分析了脱空长度和列车速度对于地铁车轨振动的影响,得到如下结论:
(1)整体道床局部脱空对车体加速度、转向架加速度等车轨振动响应影响范围远超出脱空所在区域,以车体竖向加速度为例,当车速为72 km/h,脱空长度在0.4 m~2.0 m时,加速度受影响的范围在23 m~57 m之间。
(2)整体道床局部脱空会加剧车体加速度、转向架加速度等车轨振动响应,以车体竖向加速度为例,当整体道床脱空长度为2.0 m时,加速度幅值将增大13倍。
(3)在常规地铁车速情况下(低于72 km/h),车体加速度、钢轨位移和道床位移等振动响应对整体道床的脱空长度较为敏感,随脱空长度的增大而显著增大,可作为脱空监测的敏感振动指标。
(4)整体道床底部脱空对地铁车轨振动的影响较为显著,而隧道底部脱空对车轨振动的影响较小,难以通过振动变化直接观测。
