钢筋直螺纹接头螺纹副承载特征及影响因素分析

陈 科，李智斌，赵 杰，霍 达

（1.中建研科技股份有限公司，北京 100013；2.中航工程咨询（北京）有限公司，北京 100120）

钢筋直螺纹连接是目前钢筋机械连接的主要形式之一，通过直螺纹套筒与预制钢筋丝头组成钢筋机械连接接头（以下简称“接头”），接头依靠螺纹副实现两端钢筋之间力的传递，具有连接可靠、施工方便等优势[1-3]。接头连接强度和可靠性的关键在于接头螺纹副的承载性能，关于机械螺纹联接结构，国内外学者对螺纹副承载力分布进行了系列研究。陈海平等[4]采用二维有限元法研究了螺纹类型、螺距、螺纹副径向尺寸系数、啮合扣数、摩擦系数、螺纹副材料等因素对螺纹副承载分布的影响；陈守俊等[5]以切齿后的螺纹联接为研究对象，推导给出了能够对每圈完整螺纹和切齿螺纹进行受力计算的新型力学模型；高连新等[6]研究了螺纹副受力不均匀特征，并提出了外螺纹螺距不变，修正内螺纹螺距，提高螺纹副均布承载力的近似方法；陈岩等[7]采用有限元方法研究了螺纹副径向尺寸系数、摩擦因素和材料特性对螺纹副轴向力分布均匀性的影响规律。上述研究主要集中在典型的机械联接结构中，即“螺栓—被连接件—螺母”结构，而应用于混凝土结构工程的直螺纹钢筋接头采用的是“螺栓（钢筋丝头）—螺母（套筒）—螺栓（钢筋丝头）”结构，如图1 所示，与之前述机械联接结构具有不同，接头螺纹副承载分布也具有差异性。

图1 钢筋直螺纹接头示意图

本文首先基于典型机械联接结构下的螺纹副理论开展研究，通过建立同等边界条件和加载条件下的有限元分析模型及理论数学模型，利用解析解进一步验证本文螺纹副有限元方法的正确性。其次，基于相同方法对钢筋直螺纹接头螺纹副承载分布进行有限元建模，分别从接头材料E、接触摩擦系数u和预紧力Fp三方面，研究了其承载分布特征及影响规律。该研究可为后续钢筋接头性能的优化设计提供基础。

1 螺纹副有限元分析依据

1.1 螺纹副承载分布理论

发生接触并有力作用的螺纹副，其螺牙变形主要来自螺牙弯曲变形、螺牙剪切变形、压根倾斜变形、牙根剪切变形和螺纹副径向扩展、收缩引起变形的综合。机械联接螺纹副轴向力计算示意图如图2 所示。在已知螺栓螺牙综合变形εb的基础上，通过式（1）的积分关系可计算出距离螺母自由面x距离的螺栓轴向力Fx。

图2 机械联接螺纹副轴向力计算示意图

目前，关于螺纹副承载分布的解析法中，YAMATOTO 解法得到了广泛认可[4，8]，能够比较准确地反映螺纹副承载分布规律。螺纹副x位置处的轴向力Fx与螺栓作用外力Fb间的比值用螺纹副轴向力分布系数Rf表示，为：

式（2）中：λ为螺纹副轴向力分布特征参数；L为螺母有效啮合长度。

YAMATOTO 解法在螺纹副轴向力分布计算的建模中未考虑螺纹面和支撑面摩擦力的影响[8]，同时该模型主要考虑了螺纹副材料弹性变形范围内的承载分布情况，其在工程应用中具有一定的局限性。

1.2 螺纹副有限元法的解析解验证

1.2.1 螺纹副有限元计算

依据国家标准GB/T 196—2003《普通螺纹 基本尺寸》相关数据建立M36×3 的同种材料螺纹副轴对称2D 有限元模型[9-10]，如图3 所示。考虑螺纹副接触计算的精确性，针对螺牙啮合部分进行网格精细化处理。模型边界及加载条件设定为螺母下端面固定，螺栓对称轴线施加对称约束，螺栓一端施加均布载荷P作用，模型主要参数如表1 所示。

图3 M36×3 螺纹副有限元模型

表1 M36×3 有限元模型主要参数

采用面面接触方式建立螺纹副接触对，并沿螺牙轴向方向依次编号。其等效应力Mises 应力云图和螺纹副接触应力云图如图4 所示。

图4 M36×3 螺纹副有限元计算结果

1.2.2 螺纹副解析解验证

采用YAMATOTO 解析法计算同等工况条件下螺纹副承载分布，验证上述有限元计算的可靠性。采用解析法计算外螺纹弹性变形综合系数kb=4.041，内螺纹弹性变形综合系数kn=7.159，螺纹副轴向力分布特征参数λ=0.072，计算螺纹副轴向力分布系数Rf。分别提取有限元计算模型中的螺纹副接触对轴向接触力Fy，并转化为与解析法同等表示方法的轴向力分布系数形式，其结果汇总于表2。

表2 M36×3 螺纹副接触力截面轴向拉力计算

有限元与理论计算螺纹轴向力分布系数对比如图5 所示，由图5 可以看出，螺纹副轴向力分布系数使用有限元方法和YAMATOTO 方法在计算结果上具有很好的吻合性。采用上述有限元方法分析螺纹副承载分布特征具有可行性，同时，有限元方法考虑了摩擦因数对模型的影响，可以更好地应用于实际工程分析中。

图5 有限元与理论计算螺纹轴向力分布系数对比

2 直螺纹接头螺纹副承载特征

基于前述螺纹副有限元分析方法，研究钢筋直螺纹接头螺纹副承载分布特征，分析螺纹副钢筋和套筒材料弹性模量比Re=Er/Es、接触面摩擦因数u、预紧力Fp对接头螺纹承载分布的影响。

接头螺纹副有限元模型如图6 所示。模型螺纹尺寸M36×3，螺纹副啮合扣数32 扣，由左至右依次编号。模型边界条件设置为轴对称约束，钢筋一端设置为固定约束，另一端施加螺纹副在弹性变形范围内的均布载荷作用。

图6 M36×3 接头有限元模型

2.1 材料对接头承载分布影响

设置钢筋材料弹性模量Er、套筒材料弹性模量Es，研究材料弹性模量比Re=Er/Es在0.2～2 之间对接头螺纹副承载分布的影响。接头施加均布载荷P=300 MPa，螺纹副接触面摩擦因数u=0.15，接头螺纹副各扣承载分布结果如图7 所示。

图7 材料弹性模量比Re 对接头螺纹副承载分布影响

由图7 可看出，啮合螺纹副各扣承载分布以丝头结合面为轴线呈对称分布，图中以承载比例正负号区分各扣受力方向，对称轴线两侧螺纹副受力方向相反。随着套筒材料弹性模量Es减小，螺纹副各扣承载比例均匀减小。当接头材料弹性模量比Re＞1 时，接头中部螺牙承载比例大于两端螺牙承载比例，随Re增大，二者承载百分比差值呈递增趋势；当Re<1 时，接头中部螺牙承载比例小于两端螺牙承载比例，随Re减小呈递增趋势；当Re=1 时，接头各扣螺纹副承载比例相对均匀，以一侧钢筋丝头为研究对象，丝头啮合螺纹副呈两侧承载比例高（第1—3 扣、第13—15 扣）、中间承载比例低（第8—12 扣）的近似对称分布。材料弹性模量比Re对接头螺纹副各扣承载比例影响较大，这是因为弹性模量E表征了材料的弹性变形能力，接头结构中套筒属于传力过渡结构，过小的弹性模量Es降低了接头的系统刚度，在丝头结合面附近的螺牙变形增大，从而明显增加对应螺纹副承载比例（第15—18扣）；过大的弹性模量Es提高了接头的连接刚度，啮合螺纹副变形能力降低，接头在承受外部载荷时，载荷承载分布主要集中在螺纹副前几扣，而在接头中间位置的螺纹副承载比例较小。因此，接头设计时选取弹性模量相近的材料，将有助于提高接头各扣螺纹副承载分布均匀性。

2.2 摩擦因数对接头承载分布影响

设置钢筋材料弹性模量Er=2.1e5MPa、套筒材料弹性模量Es=2.1e5MPa，研究螺纹副接触面摩擦因数u在0～0.5 之间对接头螺纹副承载分布的影响。接头施加均布载荷P=300 MPa，接头螺纹副各扣承载分布结果如图8 所示。

图8 接触面摩擦因数u 对接头承载分布影响

由图8 可看出，在接头材料弹性模量比Re=1 的前提下，随着摩擦因素u的增大，螺纹副承载分布比例在套筒两端逐渐减小，而在套筒中间附近位置的螺牙承载比例逐渐增大，但接触面摩擦因数u对螺纹副承载分布影响较小，在摩擦因数取u=0 相比u=0.5 时的承载百分比最大差值仅为1%。

2.3 预紧对接头承载分布影响

设置钢筋材料弹性模量Er=2.1e5MPa、套筒材料弹性模量Es=2.1e5MPa，螺纹副接触面摩擦因数u=0.15，接头施加均布载荷P=300 MPa，研究接头施加预紧力Fp=0～0.7P之间对接头螺纹副承载分布的影响。接头螺纹副各扣承载分布结果如图9 所示。

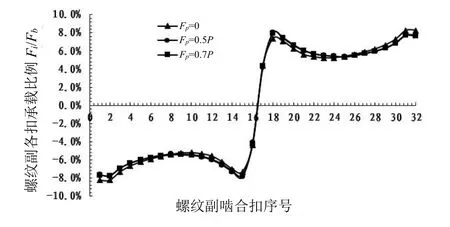
图9 预紧对接头螺纹副承载分布影响

由图9 可看出，在接头材料弹性模量比Re=1 的前提下，随着施加的预紧力增大，螺纹副承载分布比例在套筒两端逐渐减小，而在套筒中间附近位置的螺牙承载比例逐渐增大。在Fp取0～0.7P之间的值时，承载比例较大的第1 扣、第2 扣、第15 扣、第18 扣、第31 扣、第32 扣的承载百分比相差较小，最大差值仅0.6%，因此，施加预紧力对接头螺纹承载分布影响较小。

3 结论

本文建立了螺纹副有限元分析模型，结合理论解析解论证了有限元模型方法求解螺纹副承载分布的正确性。基于该分析方法，系统研究了接头材料弹性模量比Re、螺纹副接触面摩擦因数u和预紧力Fp对接头螺纹副承载分布的影响。

接头材料弹性模量比Re对接头螺纹副承载分布影响明显，弹性模量比Re取值不同，接头螺纹副承载百分比大的螺牙位置不同，选取弹性模量E相近的接头材料，可以提高接头螺纹副承载分布均匀性。

螺纹副接触面摩擦因数u和接头预紧力Fp对接头螺纹副承载分布影响较小，可以忽略。