单周期控制隔离型三相无桥Sepic PFC变换器研究
2022-07-13张纯江汤佳霖徐德勋高佳宁石炳乾
张纯江,汤佳霖,徐德勋,高佳宁,石炳乾
(1.燕山大学电气工程学院,河北省秦皇岛市海港区河北大街西段438号 066000;2.燕山大学经济管理学院,河北省秦皇岛市海港区河北大街西段438号 066000;3.国网冀北电力有限公司北京超高压公司,北京市房山区良乡工业开发区金光路3号 102488)
利用PWM控制技术实现高功率因数AC/DC变换已广泛应用于工业、电力、通信各个领域,在交流侧可以获得正弦电流,以减小谐波电流对电网的影响,同时获得高功率因数[1-2]。就直流输出而言,电压型PWM整流器或不控整流+Boost的PFC其输出电压只能在交流侧电压峰值以上调节,这给实际应用带来了许多限制,使后级变换器功率器件的电压应力增大,再者输出电压调节范围小,不能输出低于交流线电压峰值的直流电压。另外,在某些场合要求输入与输出电气隔离,目前的传统做法是采用两级变换[3-4],即AC/DC+隔离DC/DC,这种两级变换一方面使得损耗增大效率变低,另一方面变换器拓扑和控制复杂成本高。因此,研究既能够实现隔离又能使其输出可升降压调节的单级PFC-AC/DC成为电力电子研究的热点。
由于Sepic变换器具有升降压功能,且输入电流连续,易实现功率因数校正功能,因而利用Sepic变换器实现输出可升降压调节的PFC近些年有较多的研究,它分为隔离型和非隔离型。桥式整流加Sepic PFC变换器是初期提出的拓扑,将二极管整流与Sepic电路串联(相当于两级),所以效率较低,并且工作于连续导电模式(Continuous Conduction Mode,CCM)时,输出二极管存在反向恢复损耗[5]。为了提高效率和性能,研究学者逐步提出了无桥Sepic PFC,典型的无桥Sepic PFC如图1所示[6-8]。文中在拓扑图1(d)基础上构建了隔离型三相Sepic PFC变换器。
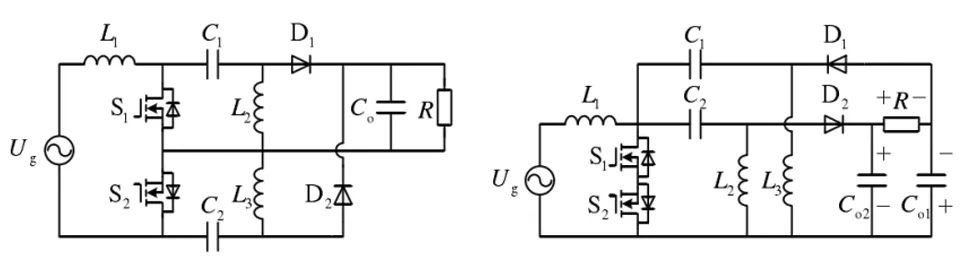
a)无桥Dual SEPIC PFC b)双向开关式无桥SEPIC PFC
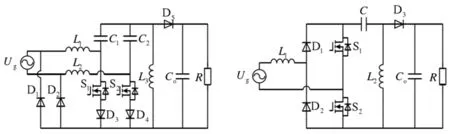
c)双二极式无桥SEPIC PFC d)图腾柱式无桥SEPIC PFC图1 四种典型的无桥Sepic PFC拓扑Fig.1 Four typical bridgeless Sepic PFC topologies
单周期控制(One Cycle Control,OCC)技术是美国学者SMEDLEY K M于1990年提出的一种新型大信号、非线性控制方法,不需要乘法器,具有调制和控制双重性[9]。它利用开关变换器的脉冲调制和非线性特性,实现了对时变电压和电流平均值的瞬时控制,有结构简单,动态响应快,开关频率恒定,对输入扰动控制强和易于实现等特点[10]。
单周期控制首先在Buck变换器中得到了验证,现已广泛应用到各种拓扑中,比如单周期控制Boost整流器[11],单周期控制Vienna整流器[12],单周期控制的单相、三相有源滤波器等[13-14]。文中提出将单周期控制技术引入三相隔离Sepic变换器中,实现了交流侧电流连续下的功率因数校正。三相Sepic PFC相较于上述拓扑有明显的优势,可实现升压输出或降压输出,可实现输入输出之间的电气隔离,输入电流连续可减小电流应力以及输入EMI的设计[15-16]。详细分析了隔离型三相Sepic PFC变换器的工作原理,分析了电流连续模式判定条件,对单周期控制的变换器进行了建模以及参数设计。设计了DSP单周期控制的实验平台,通过仿真和实验验证了拓扑工作原理和控制方法的可行性。
1 隔离三相Sepic PFC工作原理
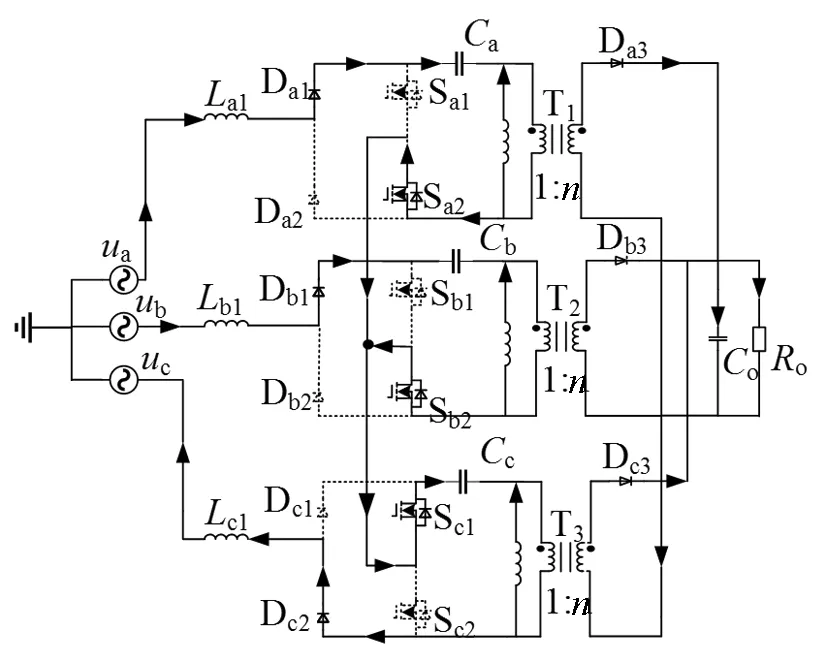
在图1(d)基础上构建的隔离型三相无桥Sepic PFC变换器如图2所示,首先将非隔离型转换为隔离型,然后将三个单相Sepic PFC并联形成三相隔离型Sepic PFC变换器。其特点为:①实现了单级隔离AC/DC变换;②输出电压可升降压调节;③单级变换效率高。④每个Sepic变换器都工作在CCM状态,每一相变换器都单独控制。
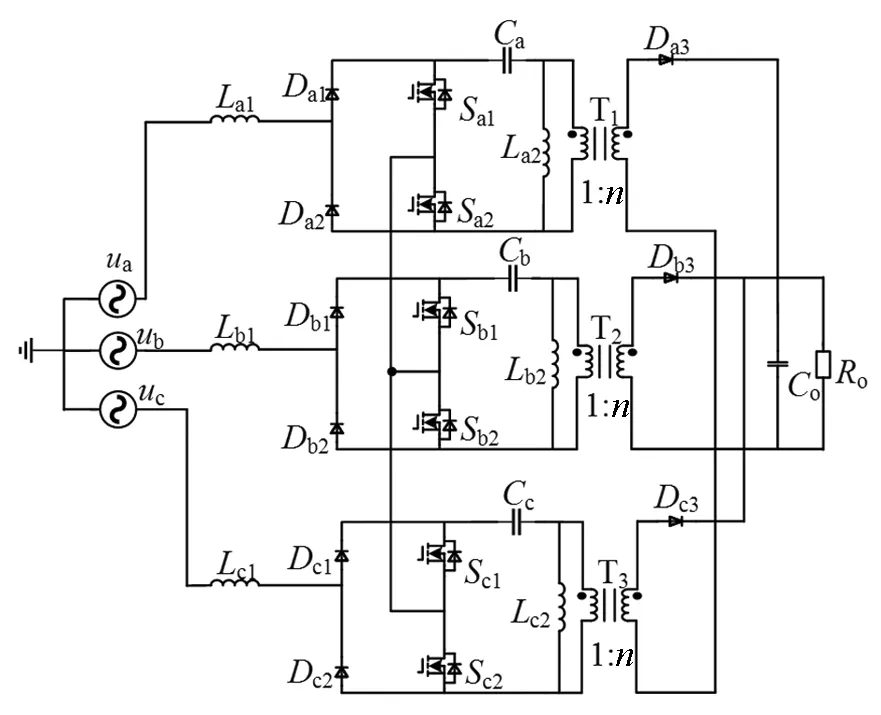
图2 三相Sepic PFC变换器Fig.2 Three-phase Sepic PFC converter
将一个工频周期内的三相交流电压分成12区间,如图3所示,下面以第5区间为例分析其工作原理。在第5区间中A相电压ua>0,B相电压ub>0,C相电压uc<0,且三相电压幅值的绝对值关系为|uc|>|ua|>|ub|,对应的主要波形如图4所示。需说明的是,电流连续模式是指在开关管的关断时间内,二极管Di3(i=a,b,c)上的电流总大于零;若二极管Di3上的电流在开关管关断时间内出现零则为电流断续模式。文中的工作原理分析是基于电流连续模式。三相中的6个开关管Sij(i=a,b,c;j=1,2)驱动信号的开通时刻相同,而关断时刻取决于电感电流iLi1(i=a,b,c)的大小。
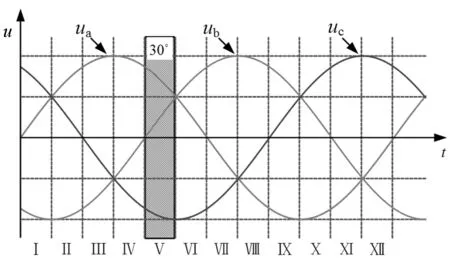
图3 一个工频周期内的三相电压Fig.3 Three-phase voltage in one power frequency period
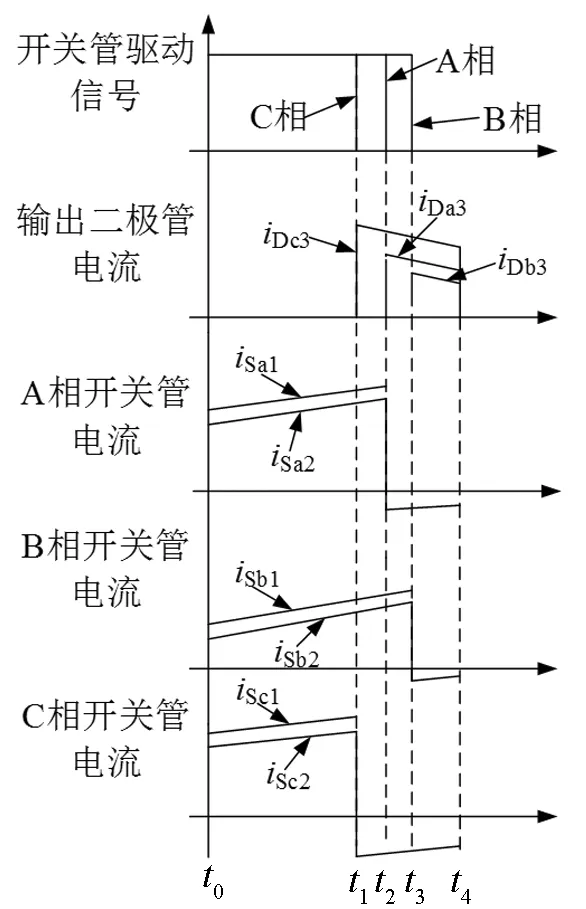
图4 主要波形图Fig.4 Main waveform diagram
模态一[t0-t1]:6个开关管同时导通,模态一等效电路图如图5(a)所示,由于ua>0和ub>0,二极管Da1和Db1导通,Da2和Db2关断,输入电压ua和ub通过Da1,Sa1和Db1,Sb1给输入电感La1和Lb1充电。由于uc<0,二极管Dc2导通,Dc1关断,uc通过Dc2,Sc2给输入电感Lc1充电。电容Ci(i=a,b,c)通过开关管Si1和Si2(i=a,b,c)给Li2(i=a,b,c)充电。所以变压器原边电压和负边电压都为负值,二极管Di3(i=a,b,c)承受反压截止,输出二极管电流为0。输出电容C0给负载供电。当C相开关管驱动信号为低电平时,此模态结束。
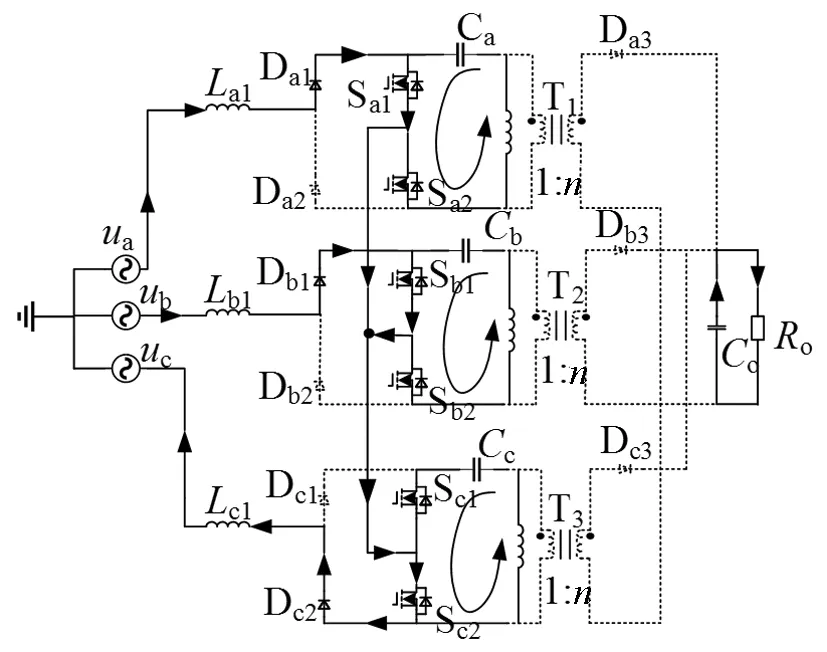
(a)模态一
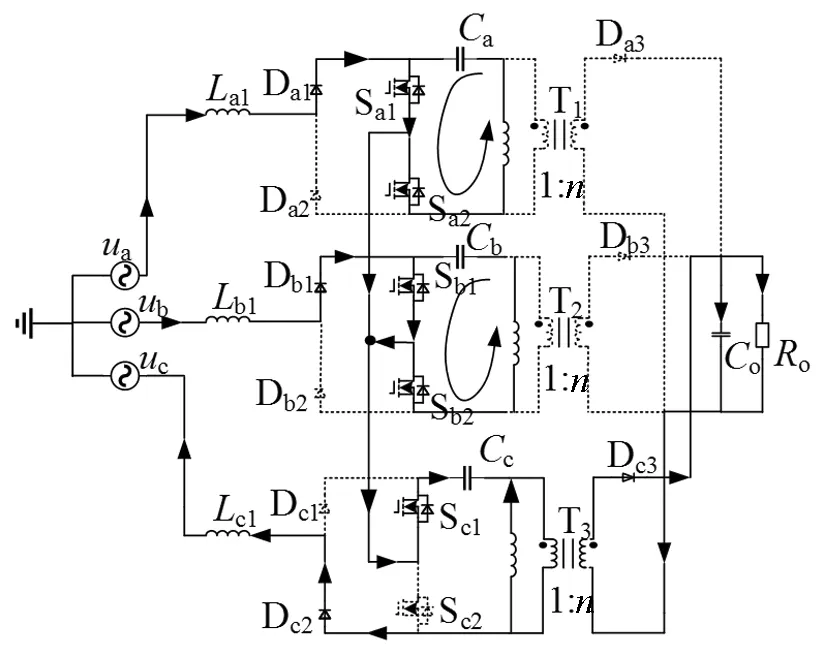
(b)模态二
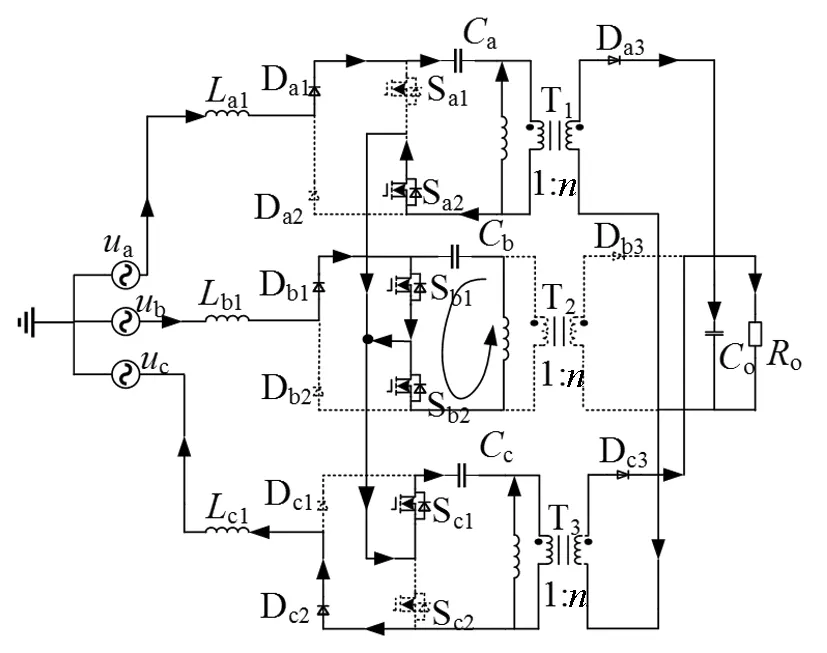
(c)模态三
(d)模态四图5 各工作模态等效电路Fig.5 Equivalent circuit of each working mode
模态二[t1-t2]:模态二等效电路图如图5(b)所示。由于单周期控制方程为(iL1×Rs+Um)×D=Um,所以电感电流iL1大的一相占空比D小,因为|uc|>|ua|>|ub|,所以C相两个开关管首先关断,二极管Dc3导通。A相和B相的工作模式和模态一相同,C相输入电压uc通过Dc2和Sc1的续流二极管给电容Cc充电并通过变压器向负载传输能量,Lc2储能通过变压器释放到负载。当A相开关管驱动信号为低电平时,此模态结束。
模态三[t2-t3]:模态三等效电路图如图5(c)所示。B相和C相工作模式和模态二相同,A相开关管关断,二极管Da3导通,输入电压ua通过二极管Da1和Sa2的续流二极管给电容Ca充电并通过变压器向负载传输能量,La2储能通过变压器释放到负载。当B相开关管驱动信号为低电平时,此模态结束。
模态四[t3-t4]:模态四等效电路图如图5(d)所示。A相和C相工作模式和模态三相同,B相开关管关断,二极管Db3导通,输入电压ub通过二极管Db1和Sb2的续流二极管给电容Cb充电并通过变压器向负载传输能量,Lb2储能通过变压器释放到负载。当下个开关周期到来时,此模态结束,并重复以上模态。
2 单周期控制Sepic PFC的基本原理
单周期控制单相Sepic PFC电路原理图如图6所示,主要由积分器、比较器、复位开关、SR触发器等模块组成。
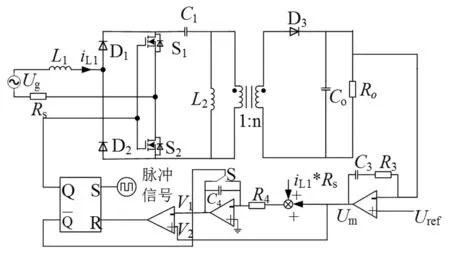
图6 工作原理图Fig.6 Working principle diagram
电流连续工作模式下Sepic电路中有:
(1)
式中,Ug和Uo分别为输入电压和输出电压,D为占空比,n为变压器副边与原边变比。
假设PFC得到很好的实现,输入电流iL1与输入电压Ug应无相位差,即变换器相当于输入端成电阻性,输入功率因数为1,此时电路应满足:
Ug=iL1×Re
(2)
式中,Re为变换器等效输入电阻。
将(2)式带入到(1)式中,可得:
(3)
对(3)式两端同乘Rs,可得:
(4)
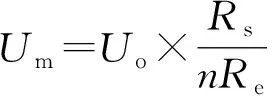
将(4)式进行变换,可得
(iL1×Rs+Um)×D=Um
(5)
式(5)为电流连续模式下单周期控制方程,如果输出电容足够大,在一个开关周期内可认为输出电压为定值,改变调制电压Um可以改变等效输入电阻Re,从而能控制Sepic输入电流iL1。
由式(5)可得:
(6)
当系统稳定后,Um可以认为是定值,根据式(6)绘制出占空比D随着输入电流iL1变化的曲线如图7所示,由图可见,占空比与输入电流成反比,在一个输入电压周期内,随着输入电流增大,占空比减小。当输入电流最大时,最小占空比约为0.48。
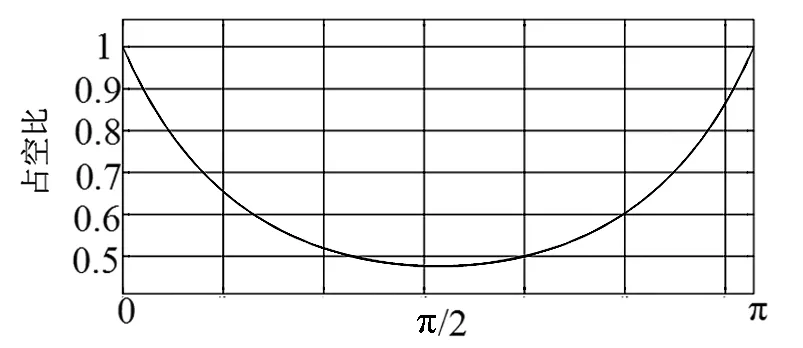
图7 占空比与输入电流关系图Fig.7 Relationship between dutween duty cycle and input current
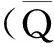
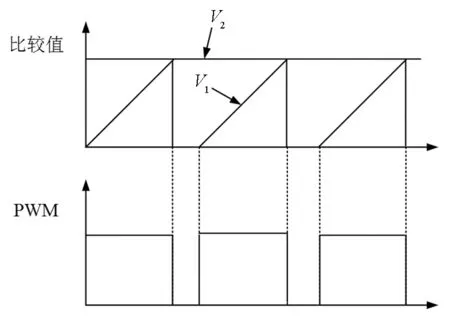
图8 单周期控制波形图Fig.8 One cycle control waveform diagram
3 电流连续条件分析
为了确定Sepic变换器的参数,必须保证变换器工作在电流连续模式。首先,设置变压比。
(7)
(8)
式中,mg为变压比,Mg为变压比的最大值,Ug,peak为Ug峰值电压。
当整流器工作在电流断续模式下,输入电流由下式决定:
(9)
Sepic变换器的变压比可由下式决定:
(10)
因此,当单位功率因数实现时,输入电流为:
(11)
将式(11)代入式(9),可得:
(12)
将式(12)化简可得:
(13)
其中,负载电阻R=Uo/Io,负载参数K=2Lfs/(R/n2)。
当整流器工作在电流连续模式下:
(14)
将式(7)、(8)、(13)代入式(14)可得:
(15)
根据式(15),若整流器始终工作在电流连续模式下,应满足:
(16)
若整流器工作在电流断续模式下:
(17)
4 线性平均模型
图9为单周期控制模式下的Sepic PFC变换器的大信号模型。该模型基于无损耗电阻的概念。变换器等效输入电阻Re吸收的功率通过时变电源Ugig传输到输出端。变换器等效输入电阻Re取决于控制输入Um的值。单周期控制的一个独特方面是变换器等效输入电阻Re与输出直流电压Uo成正比。
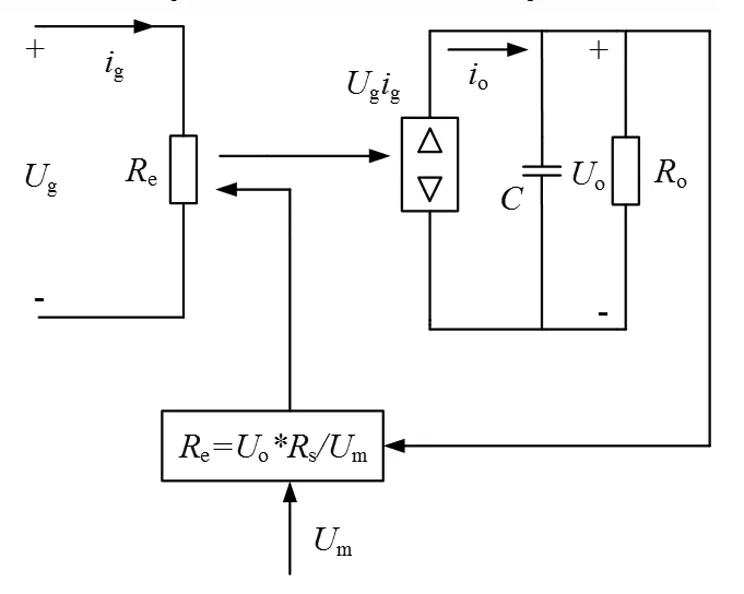
图9 OCC Sepic PFC大信号模型Fig.9 Large signal model of OCC Sepic PFC
根据大信号模型,流向负载的电流i由公式i=Ugig/Uo得出。单周期控制的Sepic整流器的直流转换特性是通过在一个周期对电流i求平均得到的。
(18)
通过对式(18)线性化可得变换器低频小信号模型,在式(18)的稳定工作点附近加入以下扰动:
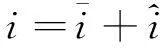
其中,“—”表示稳态分量,“∧”表示小信号扰动,代入后得下式:
(19)
将高阶分量忽略,并将稳态分量消去,可以得到:
(20)
小信号模型如图10所示,其中:
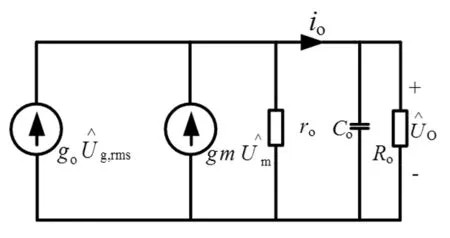
图10 小信号模型Fig.10 Small signal model
围绕图10的小信号模型设计电压调节反馈回路,如图11所示。
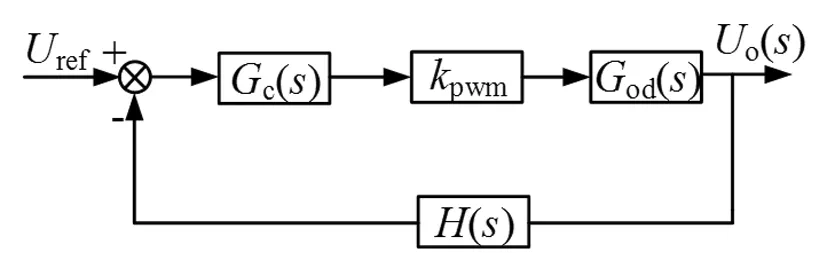
图11 电压反馈回路Fig.11 Voltage feedback loop
控制输出传递函数God(s)为:
(21)
(22)
传递函数为一阶惯性环节,转折频率为500rad/s,波特图如图12所示。
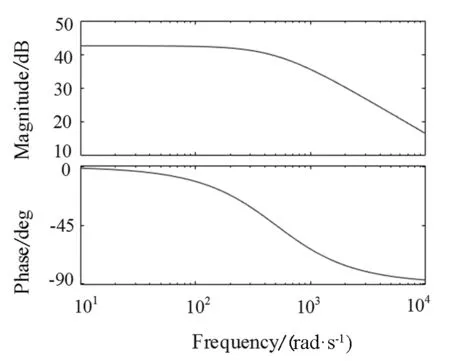
图12 God(s)幅频特性图Fig.12 God(s) amplitude frequency characteristics
想要消除系统净差,电压环调节器必须至少有一个积分环节,同时考虑系统的抗扰性能,故按照典型Ⅱ型系统设置电压控制环路。
由图11可见,单周期控制仅需一个电压环即可对电路进行控制,无需电流环,在设计电压环路时,取截止频率为fc=120Hz,相应的ωc=2πfc=754rad/s。本文采用含有一阶低通滤波器的PI调节器,由于在程序内部设置了采样系数,所以在此取H(s)=1,kpwm=1。
采用含有一阶低通滤波器的PI调节器传递函数为:
(23)
按照低频段大惯性环节的近似处理方法,将式(22)近似等效为:
(24)
所以系统的开环传递函数可以写为:
(25)
(26)
(27)
由式(26)和式(27)可以得出:ω1=251rad/s,ω2=1577rad/s。又因为k=ω1ωc,所以可以求得kc≈2.81,补偿环节的幅频特性如图13所示。
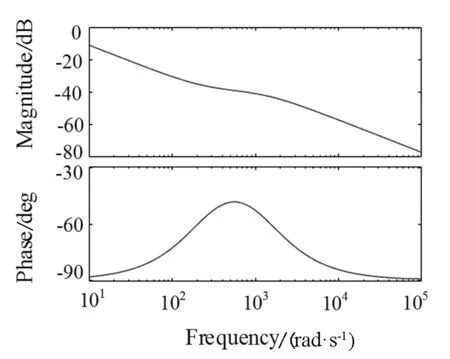
图13 电压补偿器幅频特性图Fig.13 Voltage compensator construction frequency characteristics
综上所述,系统工作时开环传递函数为:
(28)
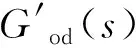
(29)
图14为式(29)近似前和式(28)近似后的开环传递函数校正后的波特图,由图可见,近似后系统的剪切频率为701rad/s,近似后剪切频率处的相位裕度为41.1°,而近似前系统的相位裕度为83.4°,说明近似前实际系统比近似后系统的稳定性更好,所以此种近似方式是可行的,并且低频段处斜率为-20dB/dec,保证了系统的稳态精度,减小静差。
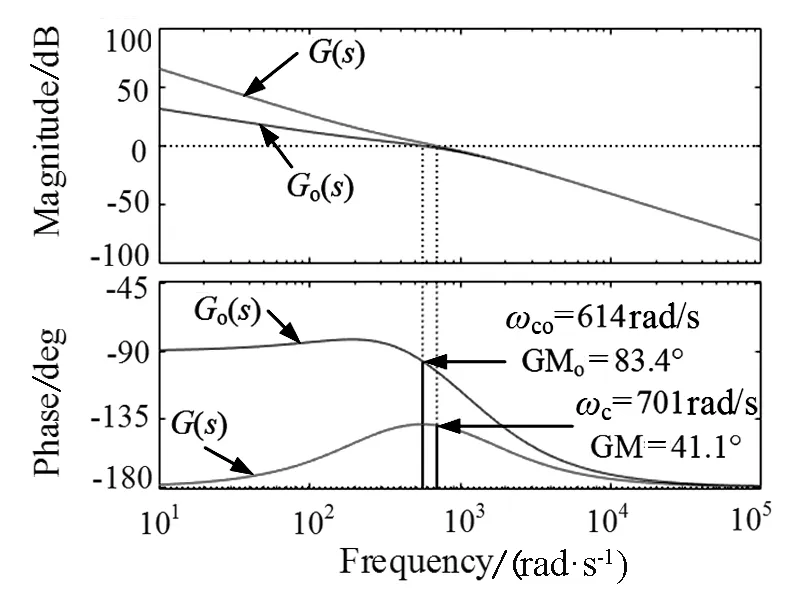
图14 补偿后的系统开环传递函数波特图Fig.14 Removal system open loop transfer function baud chart
由式(18)可得变换器的输出功率P为:
(30)
由式(30)可以得出:采样电阻Rs与变换器输出功率成反比,增大采样电阻Rs的值,输出功率会减小。
5 数字单周期控制实现
数字系统中往往采用单周期单采样的信号采样方法,由于开关频率非常高,可以认为在一个开关周期内,数字控制得到的iL1和Um为恒定值,因此可以对单周期控制方程进行变换,可得:
(31)
通过以上变换后,占空比D的值可以很容易的用DSP计算出来。其中iL1的值为采样的电感电流在一个开关周期中的峰值。图15为采用数字控制算法的单周期Sepic整流器控制框图。
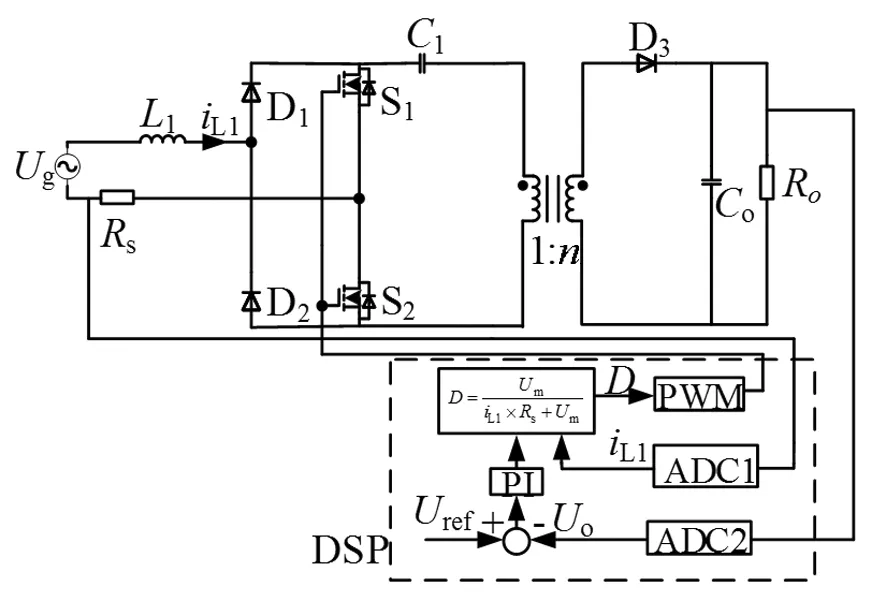
图15 基于DSP的单周期控制Sepic整流器Fig.15 One cycle control Sepic rectifier based on DSP
数字控制系统中采样频率的确定十分关键。采样频率不能太低,否则会导致数字控制器获取的系统状态信息变少,控制系统的动态性能变差;采样频率也不能太高,否则功率开关器件工作时将会形成纹波电压与纹波电流,导致系统的稳定性与控制性能变差。因此,输入电流的采样频率采用开关频率。当开关频率与采样频率一致时,可认为在一个开关周期内,电感电流iL1为恒定值。
图16中DSP采用上下计数的计数方式,这种计数方式下,可以得到对称的PWM波。在每个周期中心点(Ts/2处)进行电流采样,即可得到电感电流平均值。采样之后在(Ts/2,Ts)的时间段内完成占空比D的计算,最后选择在周期结束时刻(Ts处)进行下一个周期占空比的更新。
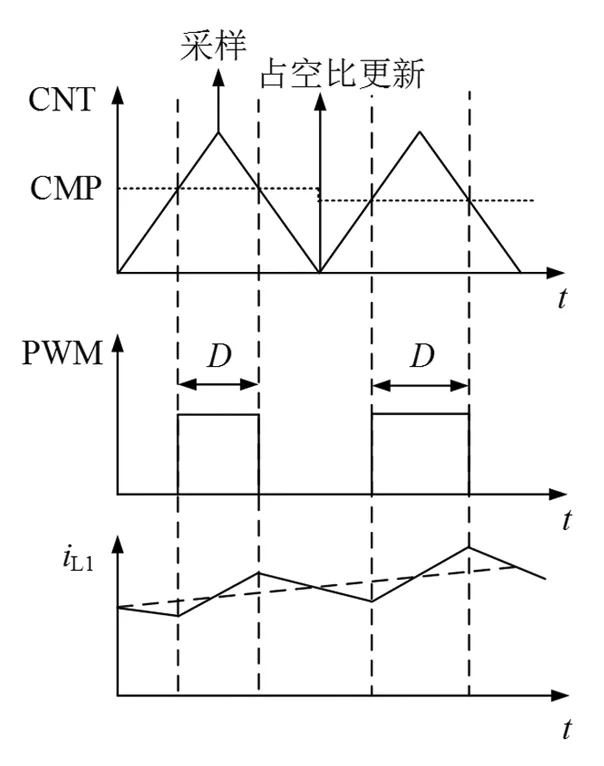
图16 电感电流采样方法Fig.16 Inductor current sampling method
6 仿真及实验验证
为验证上述理论分析的正确性,对变换器进行仿真与实验验证,三个Sepic模块参数相同,输入三相交流电压有效值Uin=110V/50Hz;工作频率20kHz;输出直流电压200V;额定功率P=1500W;电感L1=4.53mH;电感L2=8mH;中间电容C=5uF,变压器变比1:2;输出滤波电容C=1000uF;采样电阻Rs=0.02Ω。
额定负载下,输入电压输入电流与输出二极管的波形见图17,由图可见输入电流为正弦,每一相输入电流的THD约为3.1%,功率因数为0.99,接近1。由二极管电流波形可以看出,二极管电流不会下降到零,所以整流器工作在电流连续导电模式。图18为图4中第5节对应的各相驱动电压,输出二极管电流与开关管电流波形,图19为比较值V1、V2以及PWM波形,与理论分析得到的波形一致,仿真结果验证了理论分析的正确性。
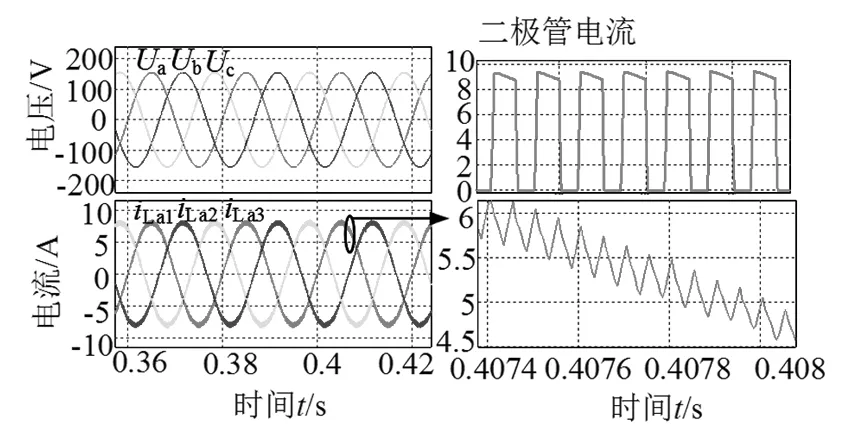
图17 输入电压电流波形与输出二极管的电压电流波形Fig.17 Input voltage and current waveform
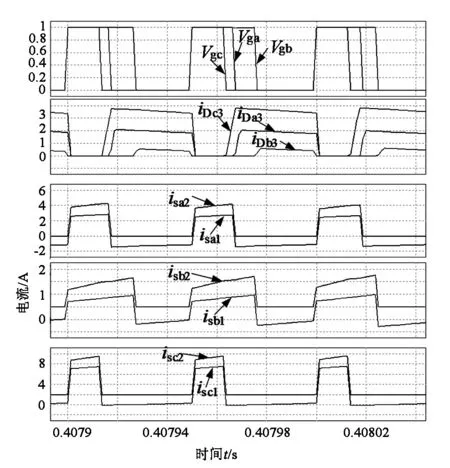
图18 驱动电压Vg,输出二极管电流iD,开关管电流iS波形Fig.18 Waveforms of driving voltage, output diode current and switching tube current
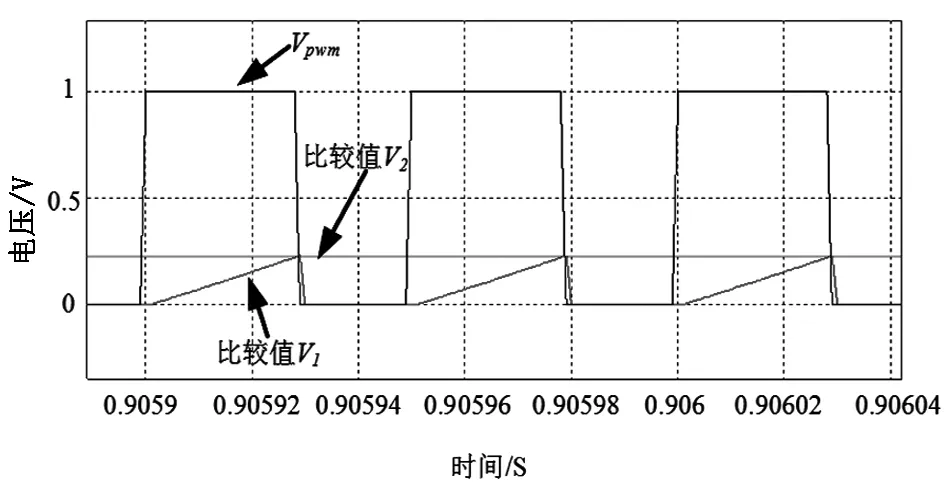
图19 PWM原理波形Fig.19 PWM principle waveform
图20为单周期控制下Sepic整流器A相输入电压与输入电流波形,由图20可见输入电流在相位上很好地跟随了输入电压,电流波形整体呈正弦状,基本无畸变,经功率计测得功率因数为0.98,THD约为6.1%。图21为输出电压波形,输出电压有一定的纹波。
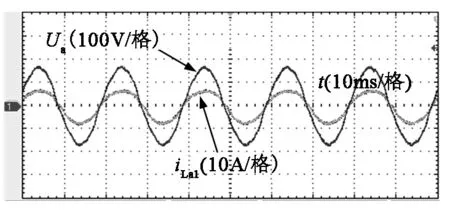
图20 电压电流波形Fig.20 Voltage current waveform
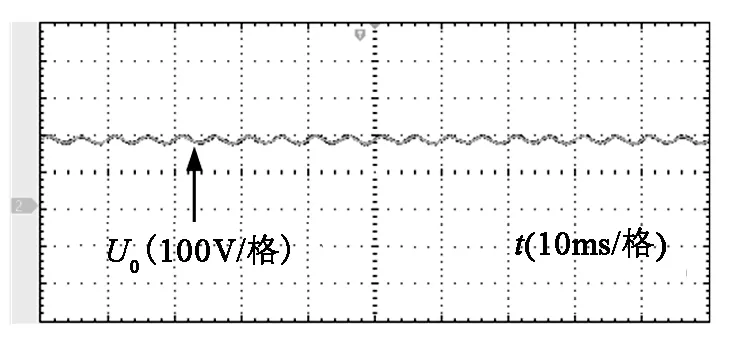
图21 输出电压波形Fig.21 Output voltage waveform
图22和图23为输入电压有效值110V,输出电压200V时,Ro在100Ω与200Ω之间切换的实验波形。由图22可知当负载突减时,输出电压在经过约60ms后进入稳态,由图23可知当负载突增时,输出电压同样经过约60ms后进入稳态,证明了系统在升压模式下的稳定性。
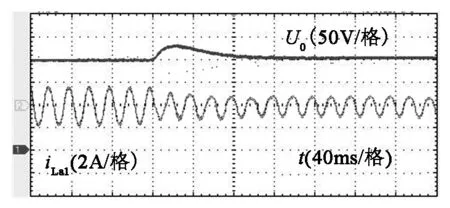
图22 负载突减波形Fig.22 Load sudden waveform
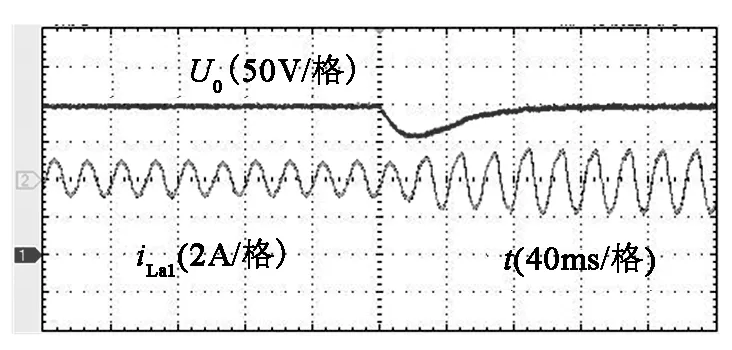
图23 负载突增波形Fig.23 Load analog waveform
7 结论
文中设计了基于单周期控制的三相Sepic PFC变换器,分析了单周期控制的基本原理及过程,从理论上分析了Sepic变换器工作于电流连续模式和断续模式的条件,对变换器进行了建模分析,并详细介绍了三相Sepic PFC变换器的工作原理,通过仿真对所设计的电路进行了验证。仿真实验结果与理论分析一致。单周期控制适用于Sepic PFC变换器,功率因数高,实现控制简单不需要乘法器,取得了良好的控制效果。
