纵凸筋板在钢管混凝土柱中的应用可行性研究

於立雄 赵 灿

(中铁房地产集团北方有限公司 北京 100166)

1 概述

钢管混凝土在工程中的应用始于19世纪[1]，由于其良好的受力性能，被广泛应用到世界各地，至今已有一百多年的历史，仍广泛应用在不同类型的工程中[2]。目前，工程中最常见的截面形式为八面形、圆形和矩形[3]，其中，方钢管混凝土是矩形钢管混凝土的特殊形式。

钢管内填充混凝土后，一方面，混凝土避免了钢管向内屈曲以至于过早发生破坏；另一方面，钢管对核心混凝土起到约束作用，提高了混凝土的强度，并改善了结构的延性和承载力，起到了一加一大于二的效果。为了更充分发挥钢管混凝土的优势，诸多学者对其轴压[4-6]、抗震[7-9]等性能进行了探讨，发现随着宽厚比的增大，管壁易发生局部屈曲，导致试件承载能力下降[10]。为了避免这一现象发生，采取了不同的构造措施，如加劲肋、拉杆[11]等，但均需要焊接等后续工艺，增大了工作量。

纵凸筋钢板是在钢板上表面带有纵向凸筋的异形钢板，其外观如图1所示。其凸筋可以增大钢管和混凝土的结合能力[12]，同时起到加劲肋的作用，提高钢板的平面稳定，并无需后续焊接等工作，可以一次成型。在日本的港口、高层建筑的钢桩、立交桥立柱等有使用内螺旋凸筋管制作钢管混凝土柱的工程实例。本文针对纵凸筋钢板这一优点，利用验证过的有限元模型，探讨其在钢管混凝土中的应用，探究不同径(宽)厚比下，不同凸筋间距对钢管混凝土柱性能的影响，并计算了单位用钢量承载力。

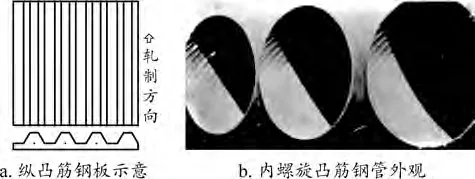
图1 纵凸筋钢板及应用

2 有限元模型建立

2.1 材料本构关系模型

假定钢材符合双线性随动本构模型，其弹性模量为2.06×105MPa，泊松比为0.3；混凝土本构模型考虑了钢管对核心混凝土约束作用等因素的影响，假定弹性模量为3×104MPa，泊松比为0.2。在导入ABAQUS时，需要转换为真实应力-应变关系。

2.2 单元选取与网格划分

凸筋、钢管、混凝土均采用八节点减缩积分格式的三维实体单元(C3D8R)。C3D8R单元对位移的求解结果较精确，且较完全积分单元减少很多自由度，大大节省了计算时间。

凸筋单独建模，后再与钢管用TIE的方法进行组合；混凝土和钢材采用面面接触(surface to surface)定义，假定法向为硬接触(hard contact)，切向采用库伦摩擦模型考虑两者的粘结效应，摩擦系数取值范围在0.2～0.6，本文采用0.25。

采用结构化的网格划分方法，对构件进行离散化。网格划分密度对计算精度非常重要，如果网格过大，计算精度降低；网格过密，将浪费过多的计算机资源。因此，网格划分时应结合网格试验来确定合理的网格密度。

2.3 边界条件及加载方式

由于使用位移法具有很好的收敛性，故采用位移加载来模拟荷载作用，一端施加法向位移约束，通过刚性端板传递竖向位移荷载；另一端固接，采用增量迭代法进行非线性方程组求解。

以圆钢管混凝土柱为例，有限元模型如图2所示。

图2 有限元模型

3 有限元模型的验证

为验证本文建模方法的准确性，从文献[3]和[13]中选取了部分试件，与本文采用的有限元模型进行比较，结果如图3所示。可以看出，本文模型可以准确地反映极限承载力和变形能力，但在下降段过程存在一定偏差，这可能与试验存在的初始偏差、人员操作等因素有关。但总体上，本文采用的模型可以有效模拟试验荷载-位移曲线，获得关键数据。

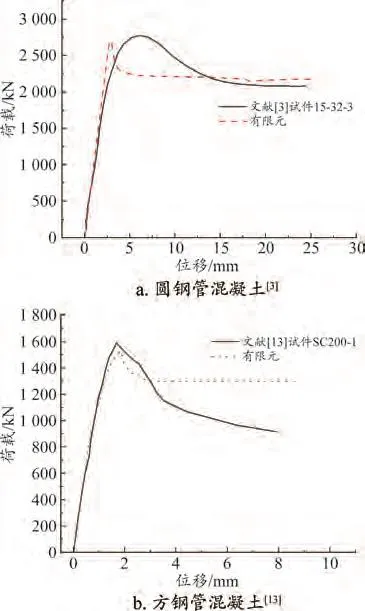
图3 有限元分析与试验结果比较

4 参数设置及结果分析

4.1 参数设置

本文以钢管混凝土柱径(宽)厚比和凸筋间距为研究参数，建立有限元模型，对凸筋板在圆钢管柱及方钢管混凝土柱中的应用进行可行性分析。假定钢材型号为Q345B，钢管壁厚10 mm；考虑现有加工水平，假定凸筋高度为3 mm，凸筋沿竖向布置；混凝土为C30等级，将其数值导入2.1章节的本构关系中。

4.1.1 圆钢管柱

为探究径厚比和凸筋间距对圆钢管混凝土柱性能的影响，依据《钢管混凝土结构技术规程 CECS 28—2012》[14]，设计了D/t＝60 和D/t＝120(D/t常用范围为(20～135)235/fy＝(13.6～92.0)两组试件，相应的套箍指标θ分别为0.5和1.7(θ常用范围为0.5～2.5)。径厚比一定的条件下，凸筋间距取0(对比试件)、50 mm、150 mm 和300 mm，共计8个试件，试件尺寸如表1所示。

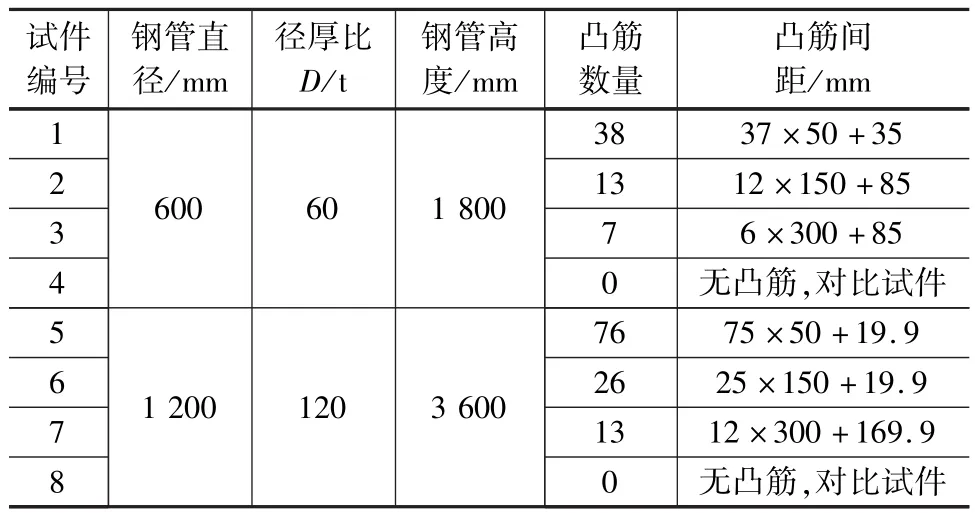
表1 圆钢管柱有限元分析试件

4.1.2 方钢管柱

为探究宽厚比和凸筋间距对方钢管混凝土柱性能的影响，依据《矩形钢管混凝土结构技术规程CECS 159—2004》[15]，设计了b/t＝30 和b/t＝70两组试件(轴压柱b/t限值为)，混凝土的工作承担系数αc分别为0.3和0.5(αc常用范围为0.1～0.7)。径厚比一定的条件下，凸筋间距取0(对比试件)、50 mm、100 mm、200 mm 和300 mm四组，共计10个试件，试件尺寸如表2所示。

表2 方钢管柱有限元分析试件

4.2 应力分布

4.2.1 圆钢管混凝土柱

不同径厚比下，不带肋和带肋(凸筋间距50 mm)的圆钢管混凝土柱在极限承载力状态下的Mises应力云图如图4和图5所示。可以看出，添加纵凸筋可以有效改善钢管部分的受力，使得钢管受力更加均匀，使钢管性能得到更充分发挥；对于混凝土部分，纵凸筋的添加同样使其受力更加均匀，但是效果较为有限。

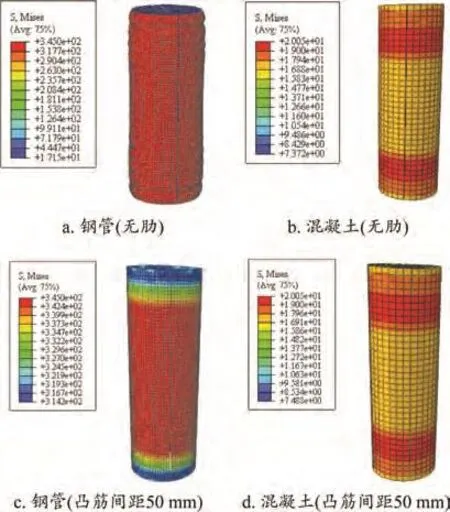
图4 D/t＝60圆钢管混凝土柱MISES应力云图

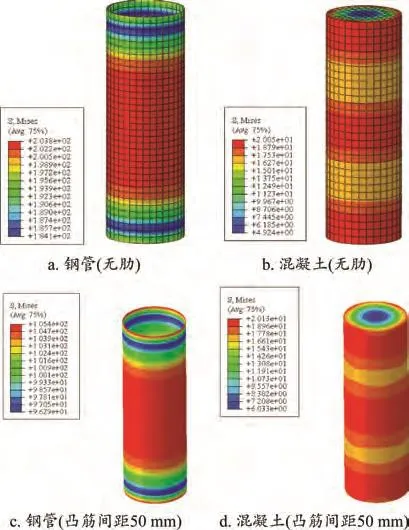
图5 D/t＝120圆钢管混凝土柱MISES应力云图

4.2.2 方钢管混凝土柱

不同径厚比下，不带肋和带肋(凸筋间距50 mm)的方钢管混凝土柱在极限承载力状态下的Mises应力云图如图6和图7所示。可以看出，添加纵凸筋可以有效改善钢管部分的受力，使得钢管受力更加均匀，有效改善了角部出现的应力集中，使钢管性能得到了更充分发挥；对于混凝土部分，纵凸筋的添加同样使得受力更加均匀，改善了角部的应力集中现象，但是效果相对不明显。

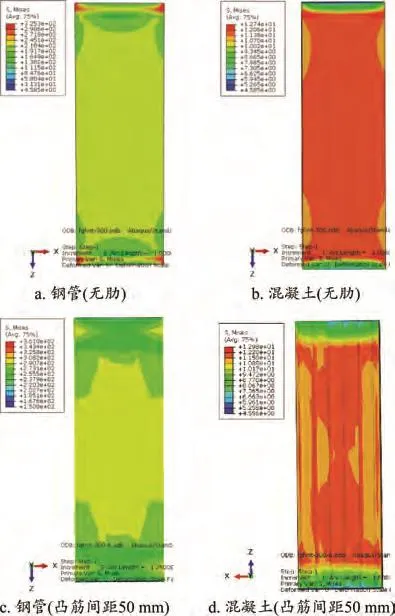
图6 b/t＝30方钢管混凝土柱MISES应力云图

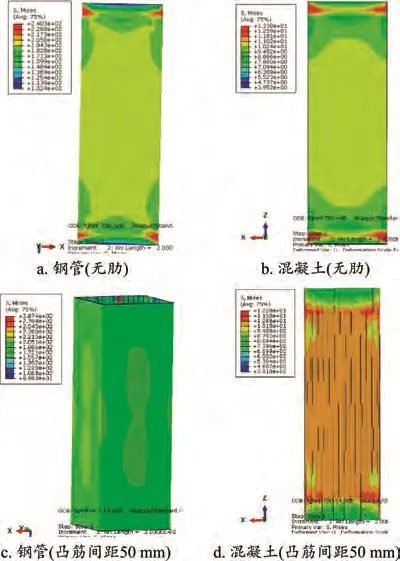
图7 b/t＝70方钢管混凝土柱MISES应力云图

4.3 荷载-位移曲线

各试件的荷载位移曲线如图8和图9所示。可以看到，随凸筋间距的减小，圆钢管和方钢管混凝土柱的极限承载力分别提高了8%和5%左右；当凸筋间距大于200 mm时，其承载力与无肋试件差别不大。刚度也有小幅提升，但不明显，这与用钢量的增加有关。同时，纵凸筋的添加在径(宽)厚比相对较小时有效改善了试件屈服后的变形能力，即使只在间距为300 mm时，其变形能力仍提升了10%，有效提高了钢管混凝土的变形能力。

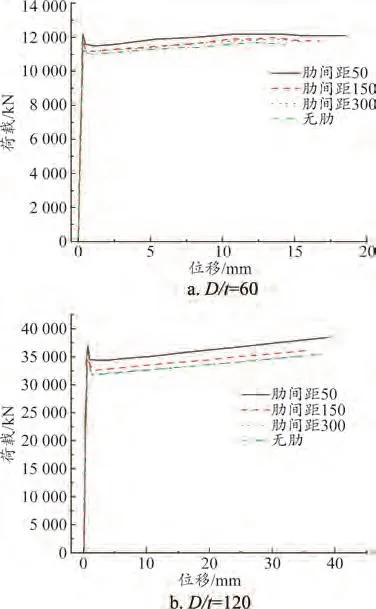
图8 圆钢管混凝土柱荷载-位移曲线

图9 方钢管混凝土柱荷载-位移曲线

为了确认承载力提升是由于用钢量的增加还是纵凸筋的影响，本文计算了圆钢管及方钢管混凝土柱试件单位用钢量承载力，并进行归一化处理(以对比试件单位用钢量承载力为基准，带凸筋试件单位用钢量承载力与对比试件单位用钢量承载力相除，得到归一化的单位用钢量承载力)，结果如表3和表4所示。可以看出，对于带纵凸筋圆钢管混凝土柱，当径厚比为60时，随凸筋间距减小，单位用钢量承载力逐渐降低；当径厚比为120时，则呈现出相反的趋势，总体变化区间在-2.9%～0.5%之间。

表3 圆钢管柱试件单位用钢量承载力计算结果

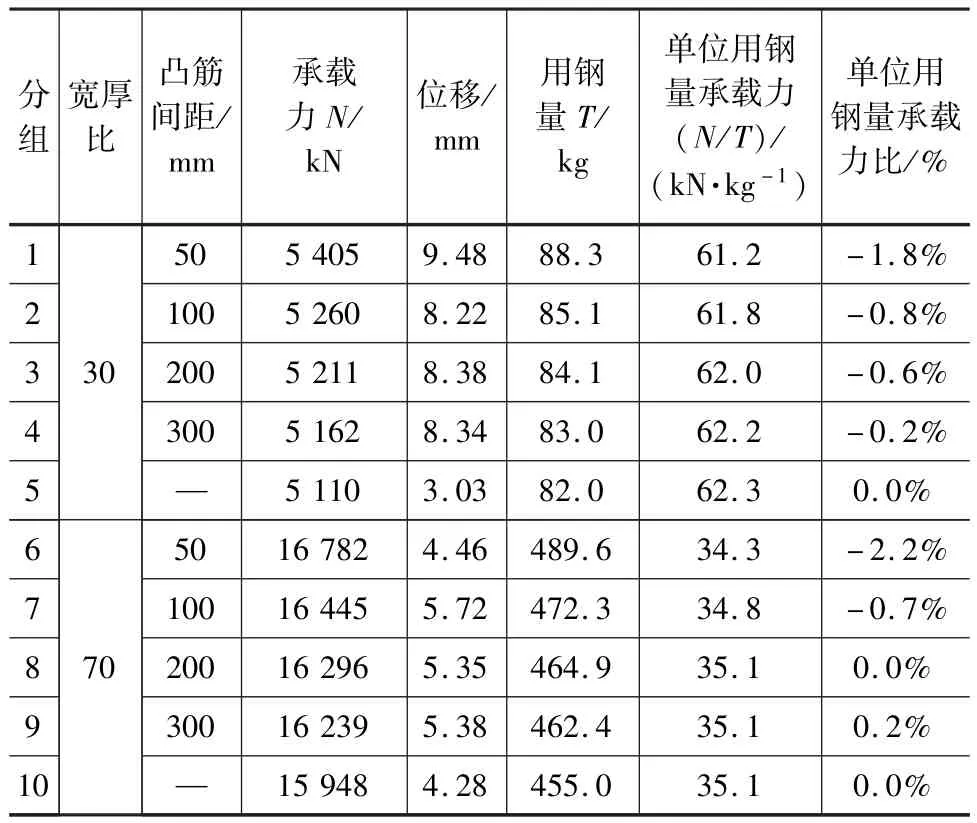
表4 方钢管柱试件单位用钢量承载力计算结果

对于带纵凸筋方钢管混凝土柱，其单位用钢量承载力变化趋势存在一定不同:当宽厚比较小(b/t＝30)时，方钢管混凝土柱随凸筋间距减小，单位用钢量承载力逐渐降低，与圆钢管混凝土柱一致；当宽厚比较大时，单位用钢量承载力同样逐渐降低，与圆钢管混凝土柱相反。单位用钢量承载力总体变化区间在-2.2%～0.2%之间。

综上，在凸筋高度为3 mm的情况下，凸筋间距在50～300 mm范围内变化时，带凸筋钢板对圆钢管和方钢管混凝土柱的承载力有一定的提高，但是相对于用钢量的提高，其提高幅度并不明显。这可能是由于带纵凸筋板上凸筋高度较小，导致凸筋刚度较弱，不能完全起到加劲肋的作用。

5 结论

为了论证带纵凸筋钢板在建筑中应用的可行性，进行了带纵凸筋建筑结构构件受力性能有限元分析。在验证有限元模型的基础上，进行带纵凸筋钢板在圆钢管混凝土柱、方钢管混凝土柱两种构件共18个试件的有限元分析，得到以下结论:

(1)带纵凸筋钢板可以有效改善圆钢管和方钢管混凝土柱的应力分布，同时在径(宽)厚比相对较小时，可以有效提高钢管混凝土柱的变形能力，提升幅度超过10%。

(2)使用带纵凸筋钢板虽然可以提高试件的承载能力，但这主要是由于用钢量提升所致，其单位用钢量承载力变化不大，变化区间在-2.9%～0.5%，这可能是由于凸筋板起筋高度较小，不能完全起到加劲肋作用导致的。

(3)为提高纵凸筋板在建筑钢结构中应用效果，建议进一步进行纵凸筋板轧制技术研究，研究起筋高度大于0.3倍基板厚度、凸筋间距小于50 mm的纵凸筋板的轧制可行性。