二元分类问题的最优分类线性降维

李炳霖, 司 梦

(1. 中国电子科学研究院， 北京 100041; 2.国网物资有限公司， 北京 100120)

0 引 言

技术的进步为社会和科技发展带来深入的变革，使我们能够以相对较小的成本来收集和处理更大规模的数据。军事领域有一类问题，需要根据采集的数据判断当前战场所处的态势、敌方的战术等，这就可以抽象为分类问题。而在现实问题中，不同态势、不同战术的外部表现往往是小差异的，其采集数据的差异往往只集中在少数特征中，即数据在分类问题中的有效特征在特征空间中是稀疏的。我们采集的数据维度越大，获取的可用于分类的差异信息就会越多，但类别间的相似特征也会越多，差异在分类维度上的聚集效应会更加明显。在实际高维数据的处理中，文献[1-3]常常加入稀疏性假设以防止过拟合和提高计算性能。

1 研究背景

本文的研究目标是高维数据的分类问题，即对新的对象进行观测得到高维数据，判断这个对象属于哪一个已知类别。

分类问题是一个很传统的研究项目，它在很多领域都有着具体的应用。如血液化验和基因领域，在学习正常和疾病情况下的数据特点后，研究者通过观测一组新的采样数据，判断被检测者究竟是正常还是异常。文献[4]通过观察动物间的交互数据来判断这种动物的社会结构是独行、分组、社区还是群居，为动物行为研究提供依据。

现代充足的高维数据为分类问题提供了新的可能，也带来了新的挑战[5-6]。样本数量相对维度的稀少使得我们无法理解数据的完整结构，而是需要进行参数估计，拟合高维模型[7]；不同类别相关关系的小差异特性，使得差异特征被相似特征掩盖，分类问题变得困难[8]。高维数据下的分类问题不再像传统低维研究那样清晰，需要更多的机理探索。

为了能够更好的对高维分布进行区分，研究差异特征的稀疏性对分类问题结果的影响，本文在前期对高斯图模型分类算法研究[9-10]的基础上，从理想高斯模型入手，将两个模型间的差异信息线性映射到多个互相独立的维度中，并基于此研究如何在保留更多可分辨差异信息的情况下进行线性降维。主要内容如下：第二章给出了高维高斯分类问题及最优分类线性降维问题的数学表述；第三章给出了分类线性降维的性质、最优分类线性降维矩阵的获取方法及其最优行证明；第四章总结上述计算结果给我们处理实际问题带来的启示；第五章对本文进行了总结。

2 问题描述

高维观测数据可以用信息空间的统计分布来建模，而观测数据可以看做是由信息空间中统计分布产生的样本。建模后的分类问题就是对不同统计分布的假设检验问题，分布间的差异可以用多种参数度量，如切诺夫距离(Chernoff Information)[11-12]、广义特征值等。

3 最优分类线性降维

3.1 线性降维特性

线性降维的过程，就是丢掉差异特征的过程。因此，在线性降维下，降低的维度越多，那么分类就越困难，降维后的低维分布间的切诺夫距离就越大，如命题1所示。

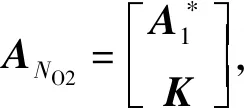
由最优分类线性降维的定义，得

因此，

虽然线性降维会丢失分布之间的差异信息，使分类变得困难，平均误差概率增大。但线性降维加快了分类的运算速度、降低了数据收集成本。对于小差异分布的分类问题，我们需要寻找最优分类线性降维，以在保留最大差异特征的前提下进行降维。

3.2 差异信息对角化

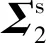
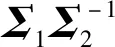
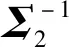
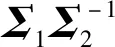
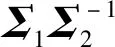
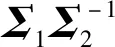
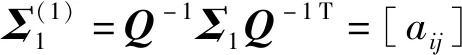
aij=λibij

aij=aji=λjbji=λibij

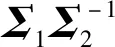
其中，J1是ni×ni可逆矩阵。

结合两步线性变换，本文可以构造线性变换矩阵

Ps=Q(1)Q-1=(Q-1Σ2Q-1T)-0.5Q-1

使得

这个命题将原来的两个高维高斯分布线性变换为两个各维度线性变量相互独立的高斯分布。通过这种方式，两个分布的差异信息被分解到独立维度上。因为线性变换矩阵是可逆的，所以这一步分解过程不丢失任何差异信息。

3.3 最优分类线性降维

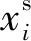
在证明命题3之前，先证明命题4。

命题4：线性降低一维后的新分布，其广义特征值与原广义特征值互相交叉。

因为可逆变换不改变协方差矩阵间广义特征值，所以它们间的广义特征值关系是具有一般性的。

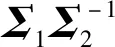
对于Σ1和Σ2，可以使用命题2得到可逆矩阵Ps使得

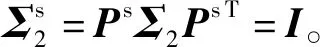
其中

a=[a1,a2,…,aN-1]T

b=[b1,b2,…,bN-1]T

是变换产生的向量。

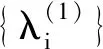
(1)

其中，fi(λ)=biλ-ai，ci是常数。

下面进行分类讨论。

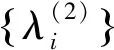
接下来基于命题4证明命题3。

证明：分布间的切诺夫距离的一种表示形式如下所示[12]：

D(Σλ||Σ2)}

(2)

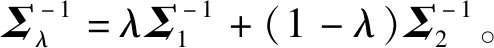
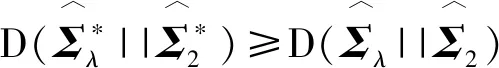
D(Σλ||Σ1)可写作

其中g(λi)=ln(λ+(1-λ)λi)+1/(λ+(1-λ)λi)-1。g(1)=0且g(λi)在区间(0,1)上是减函数，在区间(1,+∞)上是增函数。

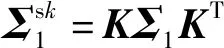
[INO,0NO×1]每次降低一维，最终得到NO维低维分布。K是任意可逆矩阵，所以这个降维过程可以表示任意线性降维。而每次降低一维的过程，降维前后的广义特征值都符合前面的交叉特性。

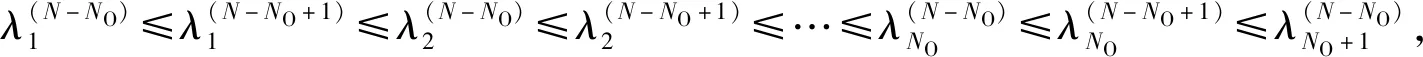
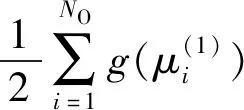
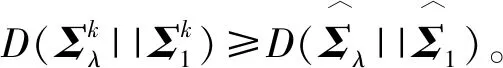
A*是所有{Aj|max {No+k-N,0}≤j≤min {k,NO}}中最优的一个，所以它在切诺夫信息上是最优的。

低维观测矩阵y=A*x的协方差矩阵为

其中{μ1,μ2,…,μNo}是最优分类线性降维选取的NO个广义特征值。注意，这些广义特征值可能包含相同值，即重数大于1。

4 数据处理问题中的启示

上述线性降维的研究，实际军事问题中的分类或识别问题提供了如下启示。

(1)寻找差异信息比寻找主成分信息更加重要

最优分类线性降维的思路与主成分分析有相似之处，都先把差异信息给分解到独立的维度上，然后再选择有着最大信息权重的维度作为降维结果。但是分解信息和选择维度的方法有着很大的区别。主成分分析只考虑一个分布，以特征值为依据进行分解，并选取最大特征值对应维度。而最优分类线性降维同时考虑两个分布，以广义特征值为依据进行分解，并选取远离1的广义特征值对应的维度。

按照常规思路，我们在对高维数据进行降维时，常常倾向于保留其主成分，使得降维过程中损失的信息最少，即降维后的低维数据能够最大限度还原高维数据全貌。常见的图像有损压缩算法都属于此类。可针对分类问题时，我们关注的不是信息的主体内容，而是多组信息之间的差异内容。因此，在小差异的前提下，常规主成分降维思路很可能会丢掉大量的差异信息，使得分类准确度大幅降低。

以两幅小差异图片压缩举例，常规主成分降维得到的是两幅模糊图片，而最优分类线性降维得到的是差异部分的切片。虽然最优分类线性降维后，我们无法了解原图全貌，但两图差异会比常规的主成分降维更好分辨。

(2)协方差矩阵的广义特征值可以用来度量两个分布之间差异的集中程度

命题2将两个高维数据线性映射到多个独立维度中去，两组数据的差异就会清楚的体现到各个维度上。当两者均为高维高斯分布时，其协方差矩阵广义特征值{λi}的分布可用来度量两个分布之间差异的集中程度。我们对不同的广义特征值{λi}情况进行计算，观察最优分类线性降维的结果。

情况1 ：考虑{λi}包含大量1广义特征值的情况，即

N=100

降维后的切诺夫矩阵随维度变化曲线如图1所示。

图1 情况1切诺夫距离随维度变化曲线

观察图1可以看到：最优分类线性降维比随机的其他线性降维方法得到的切诺夫距离要高；在降维到NO=50以前，最优分类线性降维得到的低维分布间切诺夫距离不变。因为在降维到50以前，我们舍弃的1广义特征值对应的维度，而这些维度不提供用于分类的差异信息。

情况2： 考虑{λi}远离1的情况与情况1进行对比，即

N=100

降维后的切诺夫矩阵随维度变化曲线如图2所示。

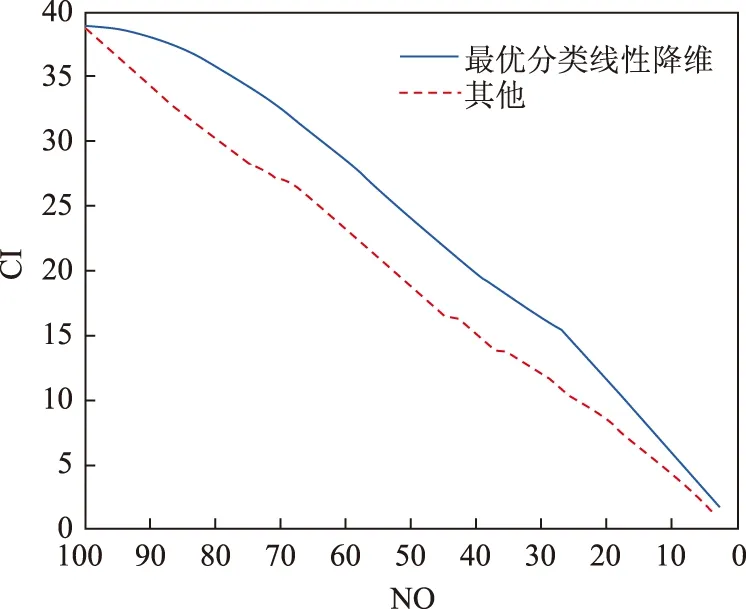
图2 情况2切诺夫距离随维度变化曲线

比较图2和图1，我们可以看到：若{λi}大部分集中在1附近，只有少数据1很远，则两个分布之间的差异较为集中，用很低的维度进行线性降维仍能保留大量差异信息；若{λi}大部分距1较远，那么线性降维就会丢失大量差异信息，切诺夫距离会迅速下降。

情况3: 考虑{λi}={1/λi}的情况，即对于任意λi，均满足1/λi∈{λi}。我们对下列情况进行最优分类线性降维，降维后的切诺夫矩阵随维度变化曲线如图3所示。

图3 情况3切诺夫距离随维度变化曲线

N=100

观察降维后低维分布的广义特征值，可以看到随着降维的进行，舍弃的广义特征值在1上下交替。即依次舍弃1,1,1/2,2,1/3,3,1/4,4…。对于切诺夫矩阵的影响，λi和1/λi可大体视为等同。

5 结 语

本文从理想高维高斯分类问题出发，给出了将两个高维分布差异信息线性分解到独立维度上的方法，并以此为基础给出最优分类线性降维方法使得降维后两低维分布间的切诺夫距离最大，并给出最优性证明。该高维高斯分布上的数学计算结果，可以为高维分类问题带来启示。当我们处理高维分类问题时，首先可以基于已有数据对问题进行分析，判断该分类问题差异在线性空间上的分布情况。若差异只集中在少数维度中，那么我们就可以选取这些维度进行数据采集和处理，其他差异信息很少的数据提可以不再采集，以减少采集和处理成本，以及这些信息对用户判断的干扰。