基于EMD-PSO-LSTM 组合模型的城市轨道交通短时客流预测

2022-07-12赵明伟张文胜王克文

铁道运输与经济 2022年7期

赵明伟，张文胜，王克文，李红

（1.济南轨道交通集团有限公司第一运营有限公司，山东济南 250300；2.石家庄铁道大学交通运输学院，河北石家庄 050043；3.中铁十四局集团有限公司城市发展有限公司，山东济南 250101)

0 引言

城市轨道交通作为一种新型的交通方式，凭借速度快、运量大、舒适安全的特点得到快速发展，逐渐成为人们通勤和日常出行的首选。在早晚高峰时间段内，短时间内大量的进站客流导致线路运营的压力增大，如上海轨道交通工作日的高峰时段，部分断面客流饱和度高达130%[1]。及时对客流进行预测，特别是把握客流的短时变化规律，有助于提高轨道交通运行效率。客流预测分为中长期预测、短期预测和短时预测。中长期预测主要应用在轨道交通线网规划与建设时期，短期预测是预测未来1年以内的客流量，这两种时间跨度的预测对于日常运营阶段的帮助不大。短时预测是预测未来15 min之内的客流量，其对于工作计划的安排以及列车的调度具有辅助作用。短时客流具有非线性、非平稳性和强随机性的特点，相比于15 min 和10 min的客流预测间隔，5 min 的时间间隔更小，客流的变化趋势更具有波动性，随机性更强，预测难度更大，预测的实用性也更强。目前，国内很多一线城市的城市轨道交通列车区间追踪时间多数小于等于5 min，因而5 min 的短时客流预测结果，对于城市轨道交通的运行调度具有很大的帮助。

客流的预测方法主要有3 类，一类是基于数理统计的方法，一类是基于智能算法的方法，还有一类是基于组合模型的方法。基于数理统计的方法中，较为常见的预测模型有Kalman 滤波模型、差分整合移动平均自回归(Autoregressive Integrated Moving Average，ARIMA)模型[2]、季节性差分自回归滑动平均(Seasonal Autoregressive Integrated Moving Average，SARIMA)模型等[3]，基于数理统计的方法较简单、易操作，但对于非线性客流的预测准确性不高[4]。基于智能算法的方法包括支持向量机和人工神经网络等[5-7]，传统神经网络是基于浅层结构，无法捕获数据中的复杂非线性关系[8]，预测误差较大。近年来，深层结构的长短时记忆(Long Short-Term Memory，LSTM)神经网络由于在捕捉时空关系方面具有优越性能而受到广泛重视[9]。Du 等[10]利用一种深度不规则卷积残差LSTM 神经网络对城市交通客流进行预测，但LSTM 神经网络的参数较难确定。基于组合模型的方法有灰狼优化(Grey Wolf Optimizer，GWO)-小波神经网络(Wavelet Neural Network，WNN)[11]、经验模态分解法(Empirical Mode Decomposition，EMD)-LSTM[12]、小波-支持向量机等[13]，组合模型利用2 种或3 种模型的优势，有效提高模型的精度，组合模型已成为客流预测的趋势。

城市轨道交通客流的非线性和强随机性加大了预测的难度，单一模型的预测能力有限。为提高模型的预测精度，将EMD、粒子群算法(Particle Swarm Optimization，PSO)与LSTM 神经网络结合，构建组合模型对客流进行预测，既可以解决数据噪声的问题，又可以克服LSTM 参数较难确定的问题。

1 基于EMD-PSO-LSTM 组合模型的短时客流预测

1.1 经验模态分解法

EMD 是一种针对非线性、非平稳数据的分解方法，该方法不需要人为设定参数，依据数据自身的时间尺度自适应地将数据分解为几个内涵模态分量(Intrinsic Mode Functions，IMF) 和1 个残差(Residual，Res)，每个IMF 具备原数据在相应时间尺度上的所有波动信息。分解完成后，IMF 需要满足2 个约束条件：在整个数据段内，极值点的个数和过零点的个数需要相等或者相差最多不超过1 个；在任意时刻，由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的平均值为0。

设客流数据为x(r)=(x1，x2，…，xr)，其中xr为第r个时间段内的进站客流，EMD 分解的步骤如下。

步骤1：找到原客流数据x(r)的所有极值点，并利用三次样条插值法绘制出x(r)的上、下包络线，分别记作emax(r)和emin(r)。

步骤2：根据上下包络线的均值绘制出均值包络线，记为u(r)。

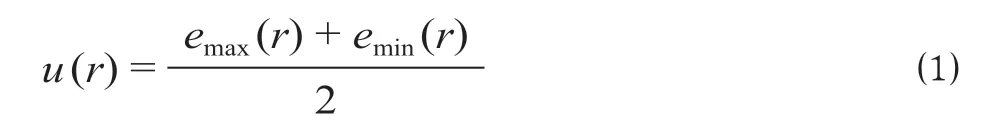
步骤3：利用原数据x(r)减去均值u(r)，得到数据v(r)。

步骤4：判断v(r)是否满足IMF 的2 个约束条件，如果满足，v(r)即为分解出的IMF，记为w(r)，如果不满足，则以v(r)为基础重复步骤1 至4；残差项R(r)为

步骤5：重复k次步骤1 至步骤4，直到残差R(r)变为单调函数或者小于预设误差，分解结束。

经过5 步的分解，原数据x(r)被分解为k个IMF 和1 个残差，即

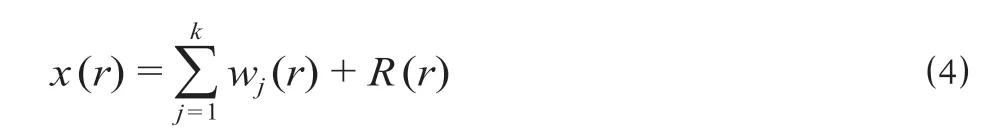
1.2 粒子群算法

PSO 最早由Eberhart 和Kennedy 于1995 年提出，是一种全局搜索最优值的算法。PSO 具备原理简单、可调整参数较少、易于实现、智能化、并行性等优点，非常适合对LSTM 神经网络的参数进行寻优。假设在d维搜索空间中，粒子群中有N个粒子，其中第i个粒子在d维空间中的位置为Xi=(Xi1，Xi2，…，Xid)，Xid为第i个粒子在第d维空间的位置；第i个粒子的速度为Vi=(Vi1，Vi2，…，Vid)，Vid为第i个粒子在第d维空间的速度；第i个粒子的最优位置为Pibest=(Pi1，Pi2，…，Pid)，即个体最优值，Pid为第i个粒子在第d维空间的最优位置；全局最优值为Pgbest=(Pg1，Pg2，…，Pgd)，即所有粒子在搜索过程中的历史最优位置，Pgd为N个粒子在第d维空间的全局最优值。PSO 的核心就是通过不断地调整粒子的速度和位置，使粒子逐步地靠近最优位置。

1.3 长短时记忆神经网络

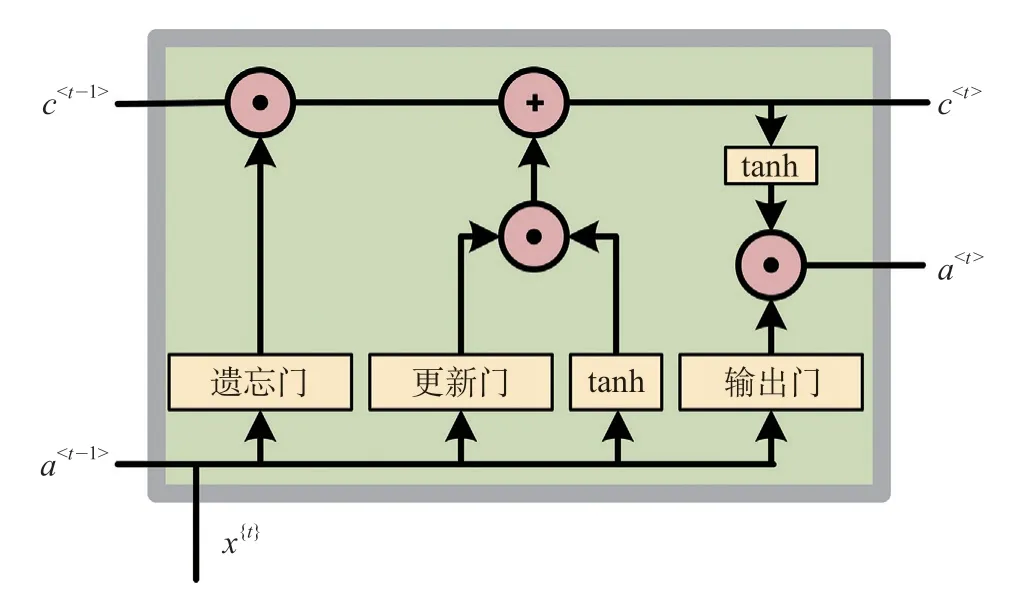
LSTM 神经网络是Hochreiter 和Schmidhuber在1997 年提出的，该网络可以进行自我衡量，可以有效弥补循环神经网络(Recurrent Neural Network，RNN)的不足。LSTM 相比于RNN，增加记忆单元，包含遗忘门、更新门和输出门，可以利用历史信息。LSTM 记忆单元拥有长短时记忆机制，适用于处理具有一定时间间隔的数据序列。LSTM 神经网络单元结构如图1 所示。图中x{t}为输入的数据；c和c分别为前一时刻和当前时刻的单元状态；a和a分别为前一时刻和当前时刻的输出。

图1 LSTM 神经网络单元结构Fig.1 Unit structure of LSTM neural network

1.4 EMD-PSO-LSTM 短时客流预测模型构建

为了提高客流的预测精度，充分利用单个模型的优点，将EMD，PSO 和LSTM 神经网络应用在客流预测中，构建EMD-PSO-LSTM 组合模型。首先，利用EMD 对客流数据进行分解，获得不同的IMF；其次，将各IMF 分别输入到LSTM 模型中，利用PSO 确定LSTM 神经网络的迭代次数、学习率和隐含层的神经元个数；最后进行客流的预测，将各个IMF 的预测结果加和，得到最终的预测结果，并进行误差分析。组合模型共分为数据分解、PSO 寻优、客流预测、预测结果分析评价4个阶段。

（1）数据分解阶段。城市轨道交通的客流数据具有非线性、强随机性的特征，含有大量的噪声，直接进行客流预测会降低预测的精度，因而利用EMD 将进站客流数据分解为不同的IMF，以此降低数据噪声的干扰，IMF 按照频率由高到低依次排列，每个分量分别代表数据中不同的时间局部特征。

（2）PSO 寻优阶段。利用PSO 优化LSTM 的详细步骤如下：①初始化粒子群参数。确定种群的规模、迭代次数、学习因子、搜索维度以及位置和速度的取值范围。②初始化粒子的位置和速度。随机生成一个粒子，Xi=(n，lr，h1，h2)，n为LSTM的迭代次数，lr为学习率，h1为第1 层隐含层的神经元个数，h2为第2 层隐含层的神经元个数。粒子的速度Vi=(Vi1，Vi2，Vi3，Vi4)，产生一组0～1 均匀分布的随机样本值，随机样本取值范围是[0，1)。③确定LSTM 的其他参数。确定预测方案为单步预测，即利用前r个历史时间段的数据{x1，x2，…，xr}预测下一时间段数据xr+1；r取值为10。④确定PSO 算法的适应度函数。用初始化后的粒子群参数构建LSTM，将训练集的实测值与预测值的均方误差作为粒子群的适应度函数f(r)。f(r)=xr为客流的实测值，为客流的预测值，N为需要预测的总的时间长度，N=210。⑤计算粒子在每一次迭代中的位置并计算适应度值。通过与初始位置的适应度值作比较，确定个体最优位置Pibest，进而确定群体最优位置Pgbest。根据公式 ⑸ 和公式 ⑹ 不断地调整粒子的位置和速度，直到适应度函数最小，确定最优位置，也就是确定LSTM 的最优参数，应用参数对各个IMF和Res 构建PSO-LSTM 模型。

（3）客流预测阶段。利用PSO-LSTM 模型对与其对应的IMF 进行预测，将各个IMF 和Res预测结果加和，得到最终的预测结果。EMD-PSO-LSTM 组合模型短时客流预测流程如图2 所示。

图2 EMD-PSO-LSTM 组合模型短时客流预测流程Fig.2 Short-term passenger flow prediction process of EMD-PSO-LSTM combined model

（4）预测结果分析评价阶段。采用平均绝对百分比误差AMAPE、均方根误差ARMSE、平均绝对误差AMAE和决定系数R24种评价指标，对短时客流预测模型的精度进行判定，各评价指标计算公式如下。

2 实例分析

基于LSTM，EMD-LSTM，PSO-LSTM，EMDPSO-LSTM 4 种客流预测模型，分别对上海城市轨道交通陆家嘴站的客流进行预测。LSTM 模型是使用标准的LSTM 对客流进行预测；EMD-LSTM模型是先利用EMD 对客流进行分解，再利用分解后的IMF 和LSTM 对客流进行预测；PSO-LSTM模型是利用PSO 确定LSTM 的参数(学习率、迭代次数和隐含层的神经元个数)，并将参数应用到LSTM 中，对客流进行预测；EMD-PSO-LSTM 模型为上述提出的模型。

2.1 客流相关性分析及数据EMD 分解

鉴于数据的可得性，选取2015 年4 月1 日至30 日期间的上海城市轨道交通一卡通刷卡数据。2015 年上海共有14 条城市轨道交通线路，313 个站点(换乘站不重复记录)，其中陆家嘴站是客流集聚中心之一，客流量较大，早晚高峰特征明显，因而选择陆家嘴站为目标站点。根据客流数量以及站点的运营时间，选取5 :30—23 :00 时间范围内的数据，时间间隔为5 min，即1 天中有210 个数据值。

周一至周五工作日的客流变化存在一定的相似性，周六日非工作日的客流变化也存在一定的相似性。研究基于1 周(2015 年4 月6 日至12 日)的客流数据，进行相关性分析。工作日与非工作日数据的相关性分析如表1 所示。

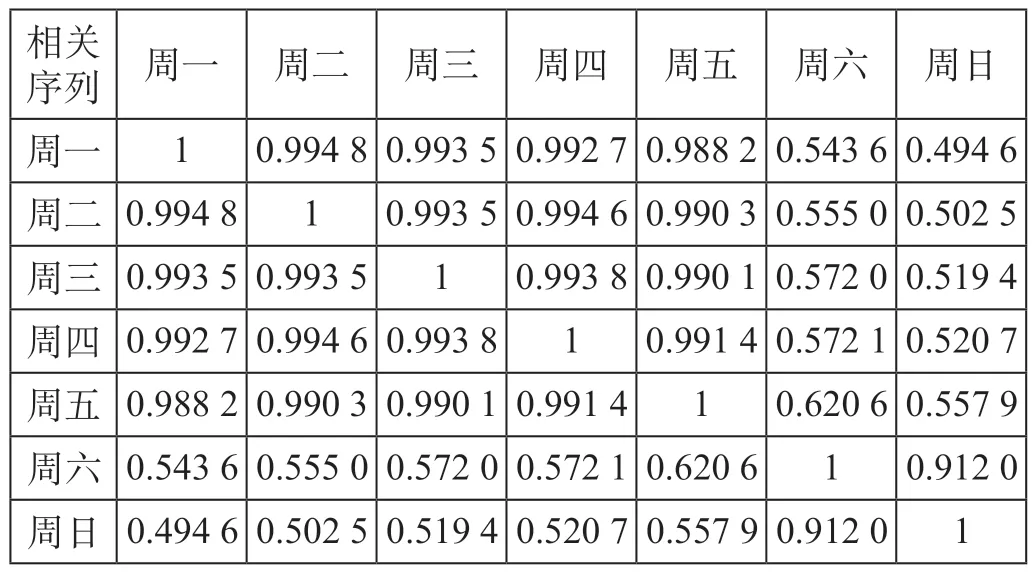
表1 工作日与非工作日数据的相关性分析Tab.1 Correlation analysis of data on working days and non-working days

由表1 可知，工作日数据之间的相关性、非工作日数据之间的相关性均较为显著，均属于高度相关性，非工作日与工作日数据之间存在较大差异，属于中低度相关性。因此，从工作日和非工作日2 个角度，研究客流预测。

对工作日和非工作日客流进行EMD 分解，工作日的客流序列被分解为12 个IMF 和1 个Res，非工作日的客流序列被分解为9 个IMF 和1 个Res。IMF 按照频率由高到低依次排列，高频分量代表原数据的主要特性，是最主要的组成分量，每个分量代表数据中不同的时间局部特征，残差代表数据的总体变化趋势。客流分解后的IMF 和Res如图3 所示。

2.2 PSO 优化

利用PSO 算法对LSTM 模型的参数进行寻优，粒子群算法的优化结果(EMD-PSO-LSTM)如表2所示，粒子群算法的优化结果(PSO-LSTM)如表3所示。

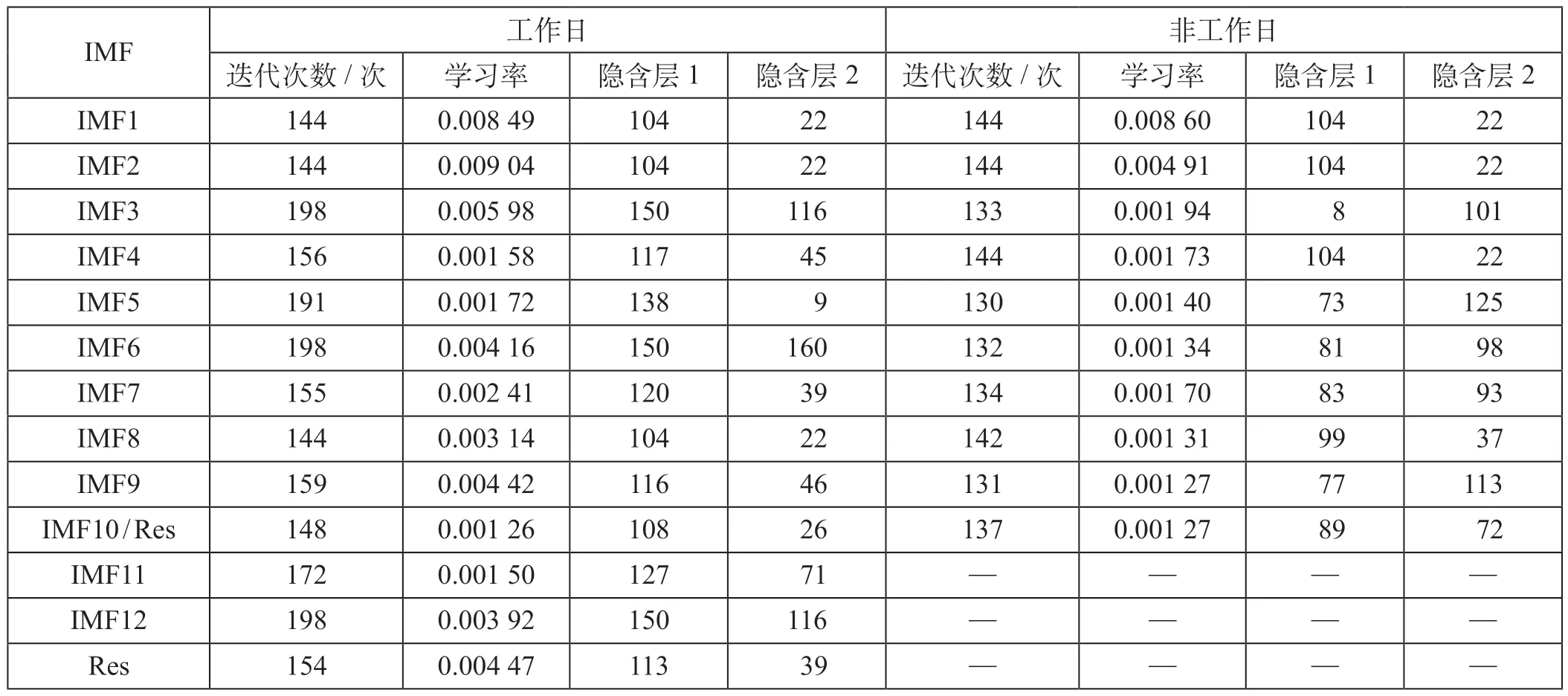
表2 粒子群算法的优化结果(EMD-PSO-LSTM)Tab.2 Optimization results of PSO (EMD-PSO-LSTM)

表3 粒子群算法的优化结果(PSO-LSTM)Tab.3 Optimization results of PSO (PSO-LSTM)

2.3 短时客流预测

（1）数据集划分。将2015 年4 月1 日至30 日期间21 个工作日中的20 个工作日的数据作为训练集，1 个工作日的数据作为测试集；9 个非工作日中的8 个非工作日的数据作为训练集，1 个非工作日的数据作为测试集，预测陆家嘴站未来1 天中210 个时间段的进站客流数据。数据集划分如图4所示。图中虚线的左侧为训练集，右侧为测试集。

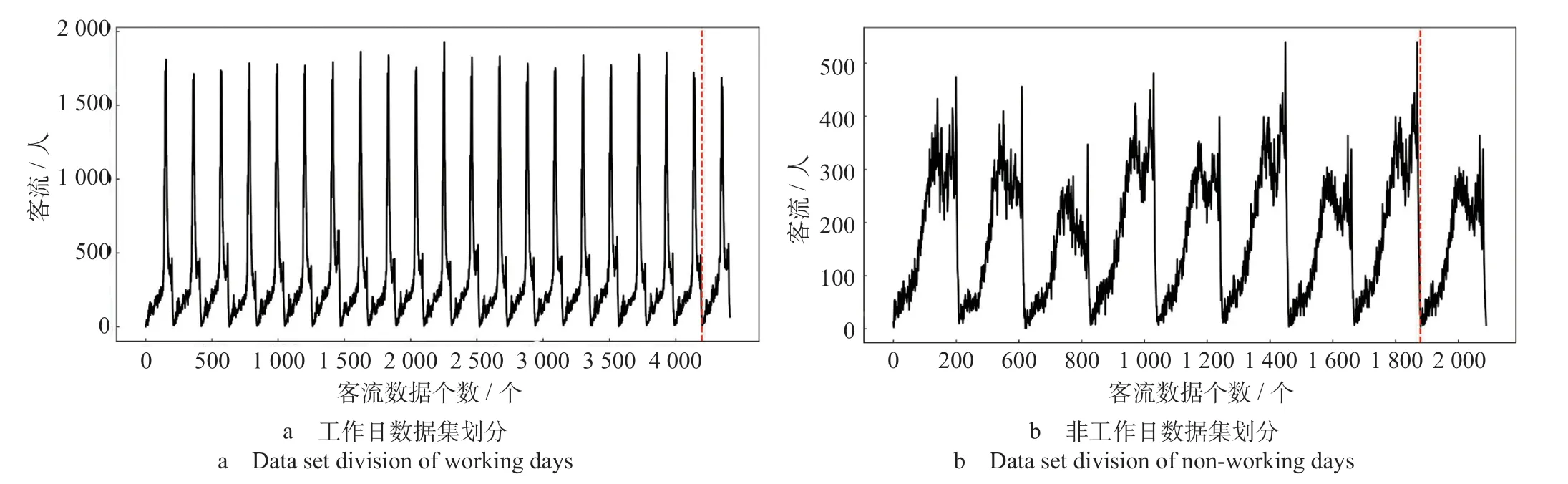
图4 数据集划分Fig.4 Data set division

（2）参数设置。在LSTM，EMD-LSTM，PSOLSTM，EMD-PSO-LSTM 4 种模型中，涉及LSTM的部分，采用2 个隐含层，1 个输入层和1 个输出层的结构，其输入层为10 个神经元，输出层为1 个神经元，采用Adam 优化器训练网络；另外，LSTM 模型和EMD-LSTM 模型的隐含层神经元个数均为50，迭代次数为100 次，学习率为0.001。涉及PSO 的部分，其参数设置为：w=0.8，c1=1.5，c2=1.5，r1=0.8，r2=0.3，粒子群数量为2，维度为4，进化次数为20 次，Xi=(n，lr，h1，h2)中n的取值范围为[100，500]，lr的取值范围为[0.001，0.01]，h1和h2的取值范围为[1，200]。

（3）预测结果。将4 种模型的预测结果进行汇总，4 种预测模型工作日客流预测结果如图5 所示。4 种预测模型非工作日客流预测结果如图6 所示。图5、图6 中，横坐标代表1 天的时间，以5 min为时间段进行划分。

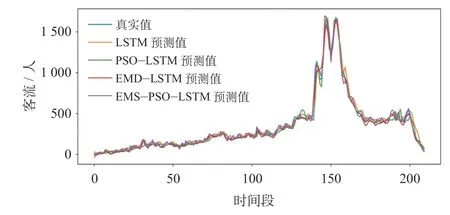
图5 4 种预测模型工作日客流预测结果Fig.5 Passenger flow forecasts of four prediction models on working days

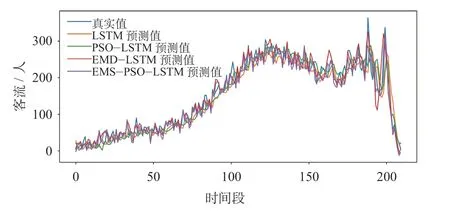
图6 4 种预测模型非工作日客流预测结果Fig.6 Passenger flow forecasts of four prediction models on non-working days

（4）分析评价。采用AMAPE，ARMSE，AMAE和R24 个评价指标对4种预测模型进行比较分析，AMAPE，ARMSE，AMAE和R2的取值为短时客流预测模型独立运行10 次之后的平均值，4 种预测模型的误差值如表4 所示。由表4 可知，EMD-PSO-LSTM模型的误差值均小于其他3 种预测模型。在工作日客流的预测中，EMD-PSO-LSTM模型较LSTM 模型，AMAPE减小37.82 %、ARMSE减小45.49%、AMAE减小42.47%，R2达到0.992；在非工作日客流的预测中，EMD-PSO-LSTM 模型较LSTM 模型，AMAPE减小45.93 %、ARMSE减小41.36%、AMAE减小41.34%，R2达到0.963。相比单一模型LSTM 模型与组合模型EMD-LSTM 模型、PSO-LSTM 模型，EMD-PSO-LSTM 模型的预测精度最高。