基于区间二型模糊神经网络的臭氧浓度预测
2022-07-12赵晓东徐浩然郭志萍任改莎
赵晓东 徐浩然 郭志萍* 任改莎
1(河北科技大学信息化建设与管理中心 河北 石家庄 050011) 2(河北科技大学信息科学与工程学院 河北 石家庄 050011) 3(石家庄市鹿泉区气象局 河北 石家庄 050200)
0 引 言
近年来,随着经济水平的提高和城市的快速发展,大气中臭氧浓度越来越高,臭氧作为一种氧化剂,也是光化学烟雾污染的重要因素[1]。但是不同于其他类型的污染物,臭氧是一种二次污染物,来自于大气中复杂的光化学反应,主要前体物为氮氧化物和非甲烷烃[2]。根据相关研究显示,臭氧浓度的升高会对人体健康产生危害,例如刺激眼睛、呼吸不畅,严重的会患上多种呼吸道疾病甚至窒息。植物在高浓度臭氧环境中会使光合作用不能正常进行,导致植物凋谢[3-4]。因此,提前准确地预报臭氧浓度有着重要意义。
目前臭氧浓度预测分为两种,一种是通过分析并建立所有影响臭氧生成的因素与最终臭氧浓度之间关系来达到预测的目的,适用于短时间的臭氧浓度预测,另一种,是将一段时间内的臭氧浓度数值按时间排成序列,通过分析建立序列之间的关系来进行臭氧浓度预测,适用于长时间的臭氧浓度预测,臭氧浓度预测问题也就转变成了模糊时间序列预测的问题。目前臭氧浓度预测都是短时间的臭氧浓度预测,可以预测出未来几小时的臭氧浓度,大多使用的都是数值模拟、多元线性回归等方法,预测精度较低。神经网络的方法被证实可以提高臭氧预测精度[5],但是在长时间的臭氧浓度预测研究比较少。模糊时间序列预测问题有自回归移动平均、粒子群优化、自动聚类和神经网络等解决方法。1965年,Zadeh教授对经典集合理论进行拓展,提出模糊集合理论,被称为一型模糊集,但是一型模糊集合在隶属度函数的选择上存在无法达成统一等问题。Zadeh教授进一步提出了二型模糊集合[6],将一型模糊集中的元素再次模糊为[0,1]区间上的数,可以解决不确定性更强的问题,但是其存在运算量过于庞大,效率低下,很难满足实际需求。Karnik等[7]提出了KM质心降型方法,并提出了区间二型模糊集的概念,区间二型模糊集合通过使次隶属度函数都为1的方法简化运算过程,使其能在实际问题上得到应用[8]。由于神经网络具有自学习、鲁棒性好且容易操作等优点,Rutkowska[9]将二者相结合,提出了区间二型模糊神经网络模型的概念;由于其具有良好的线性逼近能力,人们将其用到了医疗诊断、风电功率预测、上证指数预测、电力负荷预测等方面[10-13]。大多数区间二型模糊神经网络都是用梯度下降法、最小二乘算法和高斯牛顿法等去调节系统参数及权重,存在迭代速度过慢、计算复杂等问题。作为高斯牛顿法的优化算法,LM算法有迭代速度快、效率高等优点[14]。
综上所述,针对臭氧浓度预测难,长时间数据预测不准等问题,本文在区间二型模糊神经网络基础上,使用LM算法来调整神经网络参数及权重,提出一种用于臭氧浓度预测的区间二型模糊神经网络系统。通过基于高斯核函数的模糊C均值聚类算法进行模糊规则的筛选,筛选出的规则被用来进行区间二型模糊神经网络系统的设计。最后用2018年石家庄市国家基本气象站臭氧数据集进行神经网络的训练与测试,通过仿真研究进行验证并与使用梯度下降法的系统比较。
1 模糊聚类算法及区间二型模糊逻辑系统
1.1 基于高斯核函数的模糊C均值聚类算法(FCM)
FCM算法就是寻找数据集、聚类中心以及数据对中心隶属度所组成的目标函数的最小化,假设数据集合为x={x1,x2,…,xn},将其分为C个聚类类别,并求出每组聚类中心Vj(j=1,2,…,n)使目标函数达到最小。目标函数公式如下:
(1)
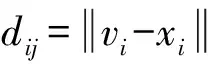
U={uij}表示隶属度函数,uij有以下约束条件:
(2)
(3)
对式(2)和式(3)使用拉格朗日算子,构建新的目标函数为:
(4)
对所有参量求导,使它们的导数等于0,对三个联立方程求解可得聚类中心vi的更新公式及隶属度矩阵uij的更新公式:
(5)
(6)
式中:i=1,2,…,c;j=1,2,…,n。
在传统的模糊C均值算法中使用欧氏距离作为距离测量方式,欧氏距离是两点在空间之中的真实距离。但是为了提高测量精度,本文用高斯核函数来代替欧氏距离。高斯核函数具有在空间中线性区分数据的能力,且具有提取数据局部特点的能力。
(7)

1.2 区间二型TSK模糊神经网络系统
模糊规则中的前件集合或者后件集合属于二型模糊集合的模糊逻辑系统被称为二型模糊逻辑系统(Type-2 Fuzzy Logic Systems),系统由模糊器、模糊规则、模糊推理和解模糊器四部分组成。

图1 二型模糊逻辑系统结构框图
准确值数据经过模糊器模糊化处理后变成模糊集,输入到模糊推理中,模糊推理的具体步骤由模糊规则决定,模糊规则采用了“if-then”规则,经模糊推理后输出模糊集,模糊集经过解模糊器再输出准确值,整个过程结束。通过模糊C均值算法进行规则筛选,去除多余的规则,有效降低计算复杂度。
区间二型模糊逻辑系统与二型模糊逻辑系统类似,主要区别是前件或后件集合为一型集合或二型集合。前件集合表示的是从模糊器到模糊推理的模糊输入集合,后件集合表示的是从模糊推理到解模糊器的模糊输出集合,整个系统也可以简单理解为由两个一型模糊逻辑系统组成,根据前件集合和后件集合的不同,区间二型TSK模糊系统分为A1-C1、A2-C0及A2-C1三种类型。通常,为了减少计算复杂度,大多数研究者倾向于对神经网络的后件部分采用确定的数据,前件采用区间二型模糊集,即A2-C0型,但是从其他文献来看,A2-C0型的准确度略低于A2-C1型,因此本文采用A2-C1型区间二型模糊神经网络。
1.3 高斯型隶属函数
二型模糊集合中的每个元素的隶属度不是确定的值,而是用一个模糊集合来表示,这个模糊集合里的元素的隶属度又由其相应的模糊集合来表示,元素的隶属度值与模糊集合之间的关系用隶属度函数来说明,所以有两个隶属度函数,区间二型模糊集合中的次隶属度函数为1,隶属度函数主要有三角形、梯形和高斯型等。其中高斯型隶属函数是普遍使用的,本文采用不确定标准差的高斯型的主隶属度函数:
(8)
(9)


图2 区间二型模糊集合高斯隶属度函数
2 A2-C1型区间二型TSK模糊神经网络系统
2.1 规则筛选
为了进一步降低算法计算度,先对模糊规则进行筛选,去掉多余的类别,本文采用模糊C均值算法进行规则筛选。假设共有n条规则,筛选出k条有效规则。
第一步:设置目标函数阈值ε、模糊加权指数m和算法最大迭代次数。
第二步:建立初始化隶属度矩阵U和数据类别的聚类中心。
第三步:由式(6)和式(5)更新模糊聚类隶属度矩阵和聚类中心。
第四步:判断收敛条件,若两次目标函数数据值之间的差值小于所规定的阈值ε,则跳到第五步。否则跳到第三步。
第五步:停止迭代,根据所得到的隶属度矩阵,取样本隶属度最大值所对应类作为样本聚类的结果。
流程如图3所示。

图3 模糊C均值规则筛选流程
2.2 结构设计
本文设计的A2-C1型区间二型模糊神经网络结构如图4所示,共有六层。
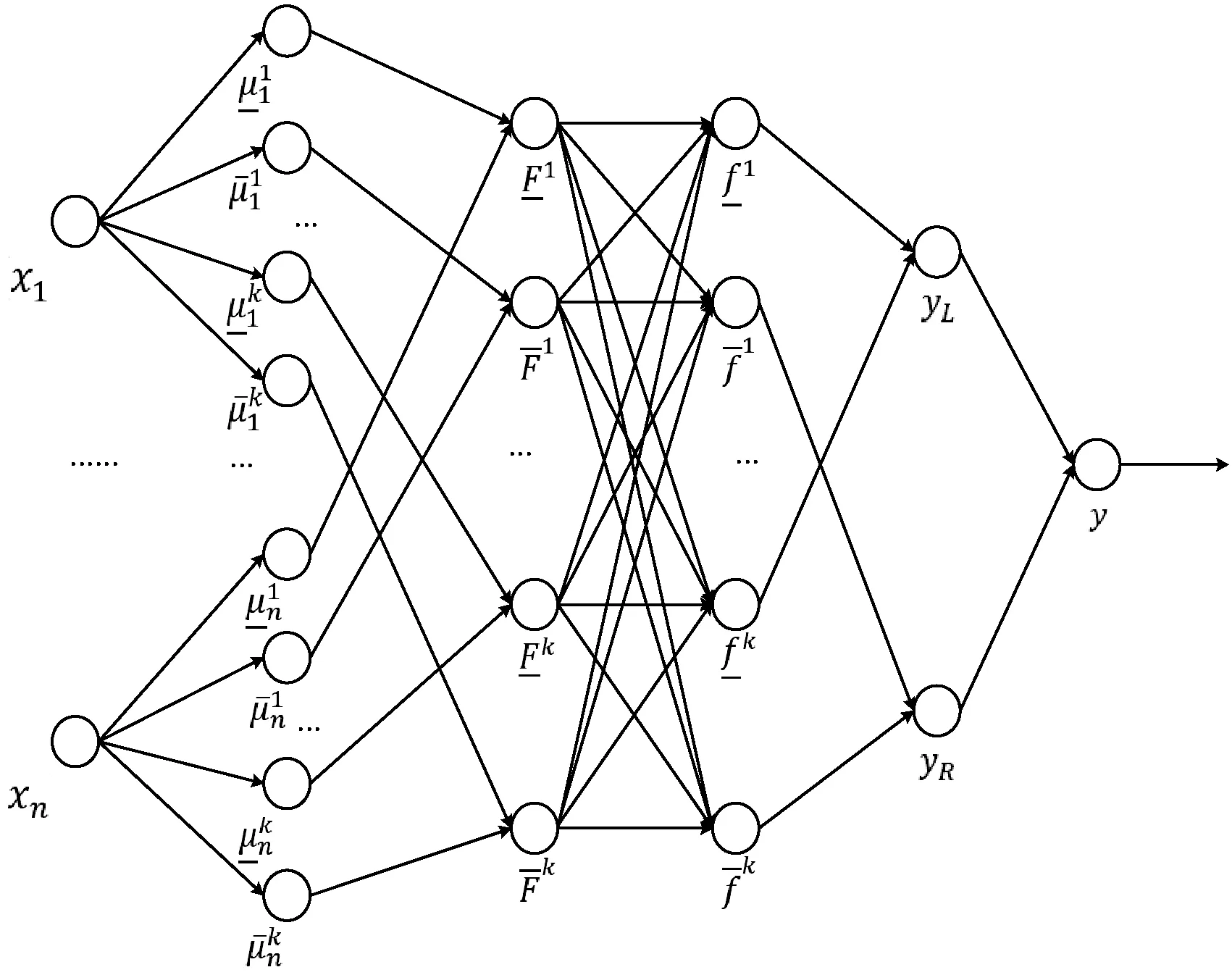
图4 A2-C1型区间二型模糊神经网络系统结构框图
该系统有n个输入,1个输出,共有K条规则,该区间二型模糊神经网络系统第i条规则如下:

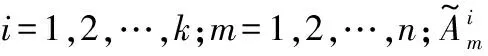
第一层:输入层:
x=(x1,x2,…,xn)Ti=1,2,…,n
第二层:计算隶属度:
第三层:计算每条规则的激发强度:
第四层:计算每条规则激发强度的权重:
第五层:计算输出的上、下隶属度:
第六层:输出层:
2.3 区间二型模糊神经网络LM训练算法
目前,BP算法是最为常用的神经网络算法,但其存在着收敛速度慢、计算复杂、对初始条件敏感等问题,需要对其进行优化。目前常用的优化方法有两种,梯度下降法(Gradient decent method)和高斯牛顿法(Gauss-Newton method)。梯度下降法的实质就是找到梯度下降最大的点,然后进行迭代,反复寻找比较各点的梯度,最终找到最小值,但是寻找各点的最小单位的选取会直接影响最终结果,最小单位过大,会找不到最小值点,最小单位过小,会导致迭代时间过长。牛顿法是一种采用二阶泰勒级数展开的最小二乘最优解的迭代方法,然而该算法需要寻找hessian矩阵,对于有着大量可调参数的复杂系统是不适用的,高斯牛顿法是将牛顿法中的hessian矩阵的2阶偏导数舍弃后实现的,该方法的迭代规则如下:
x(t+1)=x(t)-[JT(x(t))J(x(t))]-1JT(x(t))e(x(t))
式中:J是雅可比矩阵(Jacobian matrix)。
从迭代规则中看出,J(x(k))JT(x(k))可能变为单数或接近单数。为了解决这个问题,对高斯-牛顿算法的迭代规则进行修改:
x(k+1)=x(k)-[J(x(k))JT(x(k))+
μ(k)I]-1×J(x(k))e(x(k))
式中:I是恒等式矩阵,μ(k)为正值,避免了奇异矩阵求逆。从迭代规则来看,如果μ(k)为零,则两个迭代规则类似,如果选择一个较大的μ(k)值,可以忽略J(x(k))JT(x(k))值。因此,建议μ(k)从一个较小的值开始加速收敛,多次迭代后,增加μ(k)避免奇异性。此方法就是LM算法,当μ(k)值很大时,该算法近似于梯度下降法,当μ(k)值很小时,该算法接近高斯牛顿法。系统增量Δx如下:
Δx=-[J(x(k))JT(x(k))+μ(k)I]-1×
J(x(k))e(x(k))
更新规则要求计算Δx,在计算上是比较困难的,因为矩阵大小是n×n,n是系统中要更新的参数个数,为了减小计算量,建议将系统的参数分成若干组,并分别计算每组的Jacobian矩阵和LM学习速率,这将极大地减少每组中J(x(k))JT(x(k))+μ(k)I的大小,这样,用于训练区间二型模糊神经网络系统的LM更新规则为:
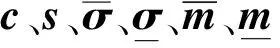
c=[c11,…,cik,…,cIK]Ts=[s11,…,sik,…,sIK]T
式中:i1为第1个区间二型模糊集输入数;i2为第2个区间二型模糊集输入数;ij为第j个区间二型模糊集输入数。此外,推出以下公式:
LM训练算法流程为:
(1) 给出训练允许期望值ε和初始化参数。
(2) 计算系统输出和目标函数E(x)。
(3) 若E(x)<ε,表明算法收敛,跳到最后一步,否则继续。
(4) 计算Jacobian矩阵和Δx,计算目标函数E(x(k+1))。
(5) 若E(x(k+1)) (6) 算法结束。 石家庄地区为本文的研究范围,石家庄市西侧为太行山区,东侧为滹沱河冲积平原,温带季风型气候,夏季高温且光照充足,冬季气温低、阳光辐射减小,且处于采暖期,雾霾数值增加导致紫外线辐射减小,高温度和高阳光辐射会促进臭氧的产生,因此夏季成为臭氧污染最为严重的季节[15]。另外,随着经济的发展,人为的氮氧化物排放也有所增加,导致臭氧浓度迅速增加,城市中的机动车排放的氮氧化物和工厂排放的VOC、氮氧化物成为光化学污染的重要根源。 图5 石家庄市2013年—2015年臭氧季节变化 选取2018年5月到8月石家庄国家基本气象站臭氧最大8小时滑动平均浓度值共计120个,用MATLAB对120个数据序列进行绘制,如图6所示。 图6 臭氧数据序列图 本实验用前四个数据预测下一个数据,共构成119组数据对,前100组用于训练系统,后19组用来测试系统,首先进行模糊筛选,确定下来15个模糊中心,即15个模糊类别。 本文选用四个输入和一个输出,第k条规则如下: 该系统各初始化参数如下: 式中:rand()为随机数。 图7为用LM算法训练的T2FLS的原始数据和预测数据跟随图。 图7 实际数据与LM算法测试数据跟踪效果图 为了验证使用LM算法的模型是否比使用其他算法预测精度更高,使用相同的模糊规则、初始参数和迭代次数,分别用BP算法和GD算法调节模糊神经网络前后件参数,与使用LM算法预测结果比较如图8和图9所示。 图8 实际数据与LM算法、GD算法测试数据跟踪效果 图9 实际数据与LM算法、BP算法测试数据跟踪对比效果 通过图8和图9来看,使用LM算法训练的模型预测结果表现好于使用GD算法和BP算法的预测模型。GD算法的表现也好于BP算法,使用LM算法的系统训练误差和GD算法的系统训练误差如图10和图11所示。 图10 使用LM算法的系统训练误差 图11 使用GD算法的系统训练误差 从图10和图11来看,在200次的迭代过程之后,使用LM算法的模型的均方误差在4.8左右,使用GD算法的模型均方误差在5.9左右,在相同的迭代次数下,LM算法比GD算法训练的模型误差要小,LM算法训练的模型要优于GD算法模型。表1展示了三种算法的均方误差值。 表1 三种算法的均方误差值 从上述实验结果来看,使用LM算法的预测模型较GD算法、BP算法在数据的训练和测试效果表现更好,均方根误差值也比GD算法、BP算法要小,这表明LM算法在调节系统参数方面比LM算法、BP算法要好,也说明了使用LM算法的区间二型模糊神经网络系统是可行的。 本文研究了基于区间二型模糊神经网络的臭氧浓度预测问题,在区间二型模糊神经网络的基础上提出利用LM算法进行神经网络参数的调整,设计出用于臭氧浓度预测的区间二型模糊神经网络系统,同时用模糊C均值算法进行模糊规则筛选,降低神经网络系统的复杂度。利用石家庄市气象站臭氧数据集进行训练和测试,进行仿真预测,并与使用BP算法、梯度下降算法的系统做比较,仿真结果表明该系统应用到臭氧浓度预测中是可行的,所设计的系统与使用梯度下降法和BP算法的系统相比有着更高的预测精度。未来的研究中可以继续对现有算法进行优化,进一步提高预测精度或者进行相关算法参数的稳定性分析,使系统更加稳定运行。3 实验与结果
3.1 石家庄地区臭氧趋势

3.2 实验数据训练及结果
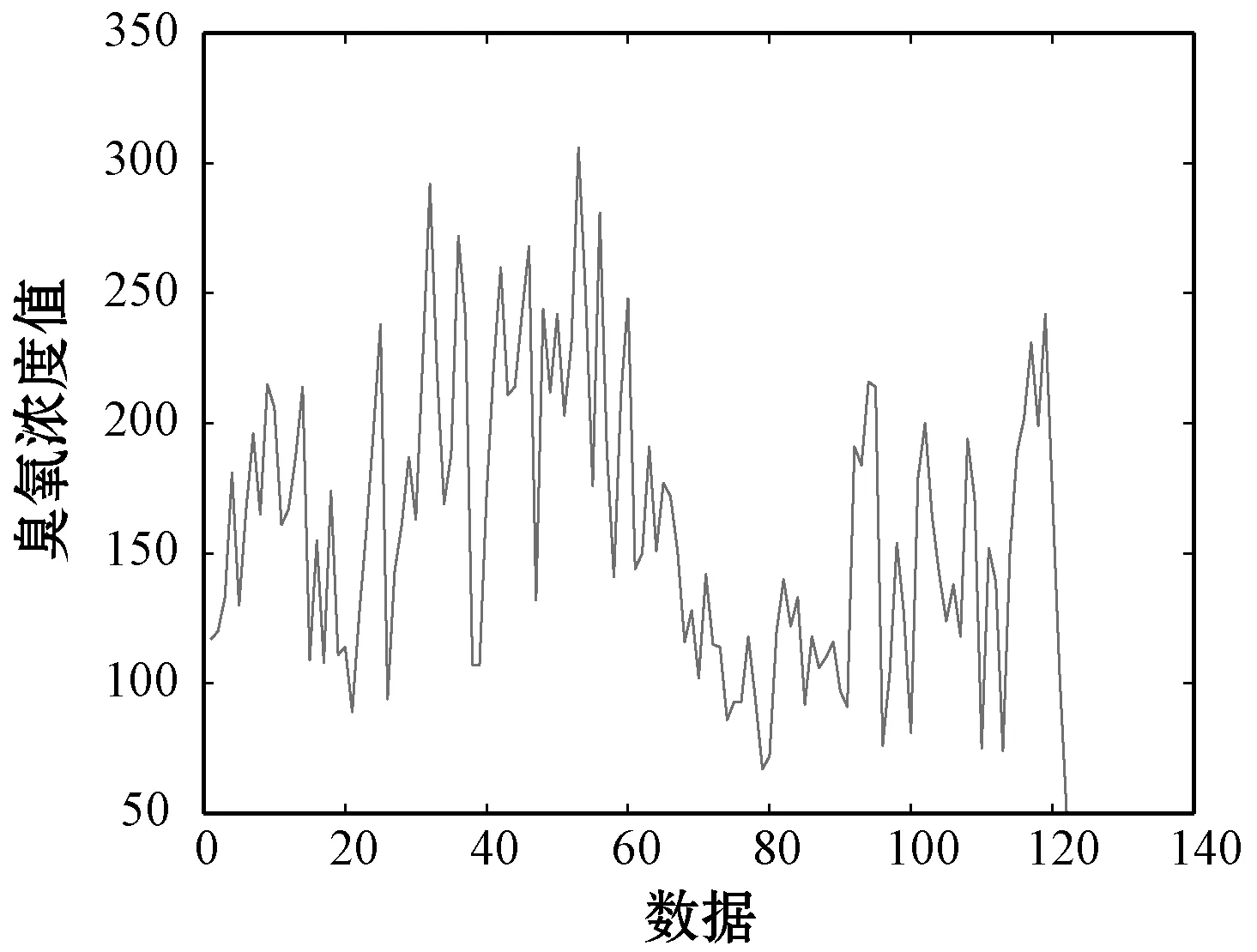
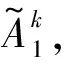
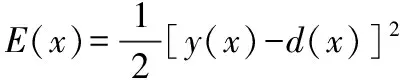

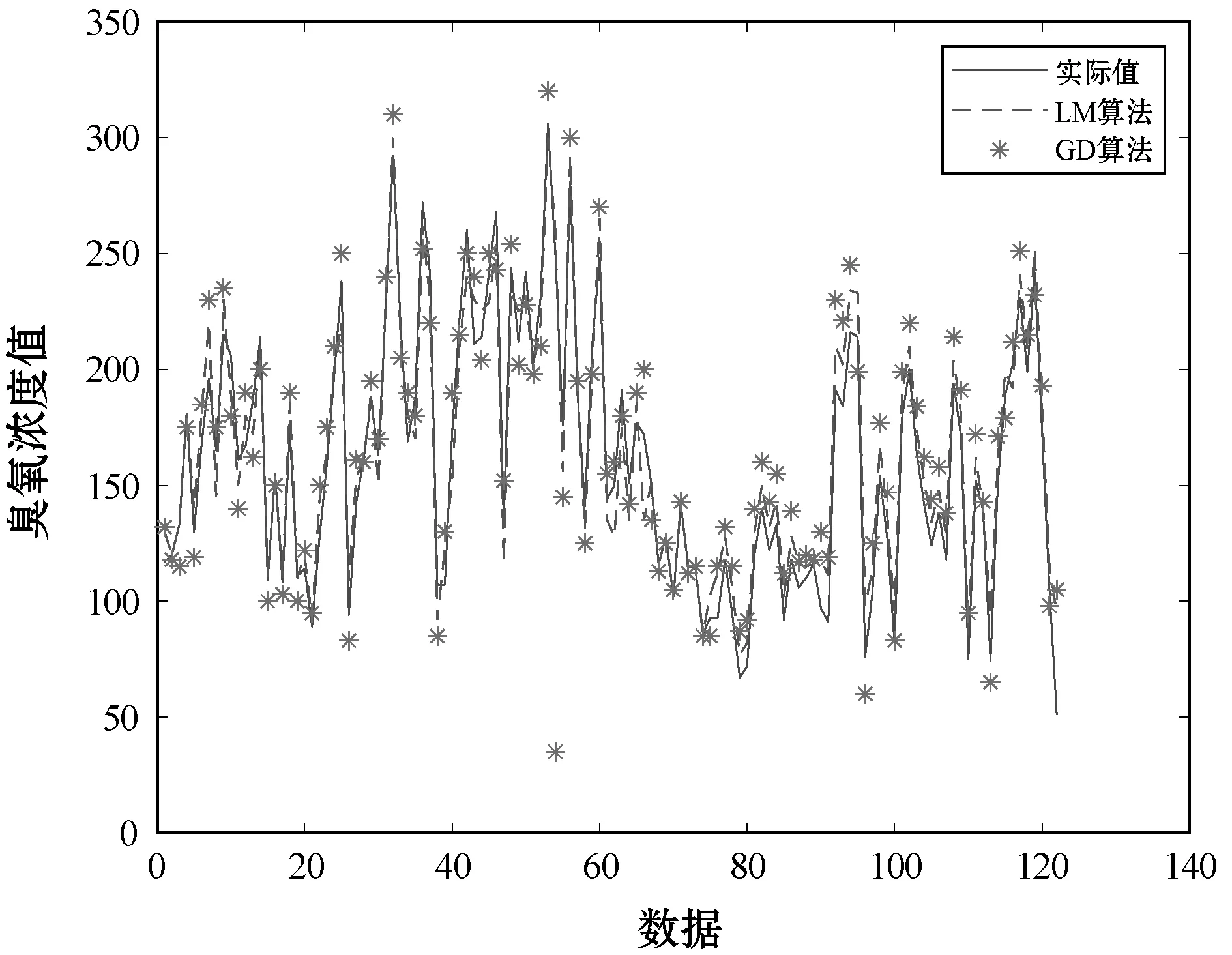


4 结 语
