一种自适应的并行化模糊挖掘算法

赵 洪 博

(复旦大学软件学院 上海 200433)

0 引 言

流程挖掘是一门比较年轻的研究学科，其基本理念是从事件日志数据中提取有价值的流程信息，从而对实际模型进行发现、监控、改进。流程挖掘的发展已经非常成熟，出现了很多挖掘算法，如α算法[1]、启发式挖掘算法[2]、归纳式挖掘算法[3]、ILP挖掘算法[4]、eST挖掘算法[5]等，这些算法通过对日志数据进行分析，得到相关的流程模型并以petri net[6]、C-net[2]等形式展现出来。尽管这些流程挖掘算法在实验条件下取得了非常好的效果，但在实际场景中，由于日志数据比较复杂且包含一些噪声数据，致使它们在实际条件下表现不佳，往往会出现过拟合现象，得到“意大利面式”的流程模型。模糊挖掘算法[7]可以比较好地解决数据过拟合问题，在实际场景中有着非常广泛的应用。文献[8]提出了将模糊挖掘算法应用到恶意软件的检测中，文献[9]提出了将模糊挖掘算法应用到软件开发行为分析中。模糊挖掘算法也存在一些缺点，包括使用该算法时需要预先手动配置参数，该过程比较繁琐，在实际应用场景中，尤其是陌生的环境下很难直接确定参数具体值；在数据处理阶段，模糊挖掘算法需要对整个数据集进行处理，当数据规模比较大时可能会影响算法的运行效率；模糊挖掘算法的建模方法不够细致，而且未能针对长距离依赖关系给出具体的解决方案。针对以上提出的几个问题，本文对传统的模糊挖掘算法进行改进，提出一种自适应的并行化模糊挖掘算法(APFM)，该算法使用起来更加简单方便，具备处理大规模数据集的能力，而且得到的流程模型也更加精确。

1 相关研究简介

目前，流程挖掘的发展面临着多方面的挑战[10]，如何提高算法的运行效率，增强算法进行大规模数据处理的能力是热门研究方向之一。在流程挖掘算法的优化方面，文献[11]提出了将mapreduce计算框架应用到流程挖掘的数据处理中，基于数据的key值对数据进行分块、排序，完成数据的并行处理。文献[12]给出了基于Hadoop完成流程挖掘任务的具体实现方法，并以归纳式挖掘算法为例进行测试。文献[13]是对文献[11]提出的算法进行改进，提出了一种基于活动关系的聚类方法将数据进行分块处理。文献[14]是使用多线程技术对启发式挖掘算法进行优化，提高了算法的运行效率。文献[15]也是对启发式挖掘算法进行优化，该算法基于Amazon Cloud实现，数据处理能力更强，应用场景更加广泛。文献[16-17]提出了将分治思想应用到流程挖掘中，开发了一种通用的数据处理方法(或算法框架)。文献[18]针对大规模数据处理场景提出了一种可横向拓展的流程发现计算框架，并给出了流程模型的一致性、完整性检测方法。文献[19]对eST挖掘算法的缺点进行分析并改进。

综合来看，这些研究都是对其他流程挖掘算法等进行优化，很少涉及模糊挖掘算法，而且它们在解决数据的过拟合问题、处理非结构化的流程模型方面没有给出比较好的解决方案。基于这个研究现状，本文将模糊挖掘算法的优化作为研究的主要方向，提出的APFM算法保留了模糊挖掘算法的优势，并对传统的模糊挖掘算法不足之处进行优化。

2 APFM算法

本文提出的APFM算法本质上也是一种模糊挖掘算法，其中的“模糊”是指根据流程日志数据挖掘大致的流程模型，并未将所有的活动一一还原出来，只是将重要活动表示出来，相连的非重要活动会被整合为一个抽象活动集合节点。该流程模型中不包含冗余的活动关系，整体的结构层次比较清晰，解决了数据过拟合问题。结合传统模糊挖掘算法的不足，APFM算法从自动化参数配置、并行优化、建模优化三个方面对其进行改进。自动化参数配置是指APFM算法可以根据日志数据计算相关的参数，实现参数的自动化配置。并行优化是指APFM算法中将涉及大规模数据处理的过程进行并行化改进，确保在处理大规模数据集时也有比较好的表现。建模优化是指APFM算法将活动、活动关系处理过程分别进行优化，并添加了长距离依赖关系的处理方法，提高流程模型的精准程度。

图1展示了本文提出的APFM算法的数据处理流程，该算法主要分为两个部分，分别是自动化参数配置过程以及流程模型的处理过程。自动化参数配置阶段需要配置包括活动重要程度参数以及活动关系重要程度参数。流程模型处理阶段又分为三个部分，分别是活动关系处理、活动的抽象与聚合以及长距离依赖关系的处理。活动关系处理包括活动关系的过滤以及活动逻辑关系的识别，确保流程模型中不包含冗余的活动关系。活动的抽象与聚合就是将部分重要程度较低的活动抽象为一个活动集合，在流程模型中区别展现出来。前两个数据处理阶段完成得到的流程模型，并未标示出长距离依赖关系。为了解决这个问题，APFM算法在最后一步计算长距离依赖关系因子，挖掘流程模型中包含的长距离依赖关系。

图1 APFM算法数据处理流程

3 参数的自动化配置

模糊挖掘的参数配置是指在算法的预处理阶段对日志数据中涉及到的每个活动、活动关系配置对应的重要程度参数，后面的数据处理过程中以这些参数为基础进行活动逻辑关系识别、活动关系过滤、活动节点的抽象与聚合。在很多实际场景中，活动重要程度以及活动关系重要程度的具体数值很难直接确定，手动设置比较困难。APFM算法中的自动化参数配置方法可以对日志数据进行分析，完成参数的自动化配置。

3.1 自动化参数配置方法的基本原理

在传统的模糊挖掘算法中，频率是衡量活动重要程度、活动关系重要程度的常用指标之一，在日志数据中出现频率越高的活动，其重要程度越高。然而在很多实际场景中，有些活动在日志中出现的频率不高，但其对流程模型的影响较大，如果直接将频率作为衡量活动重要程度指标，得到的流程模型可能不够完整、不够精确。例如，在进行程序开发时，开发新功能的工作量比较大，而进行代码评审、代码提交等工作比较少。因此，在计算重要程度时，既要考虑活动的频率，也要考虑活动对流程模型的影响程度。

定义g(A)衡量活动A对于整个流程模型的影响程度，计算方式如式(1)所示。活动对流程模型的影响程度与活动轨迹密切相关，如果某个活动在大多数活动轨迹中均有出现，那么该活动对流程模型具有比较大的影响。在式(1)中，TraceSet表示整个活动轨迹集合，t表示某条活动轨迹。统计活动A在哪些活动轨迹中出现过，并与活动轨迹总数相比即可得到活动影响因子的具体数值。例如，计算某个活动对流程模型的影响程度数值为0.98，很接近于1，表明该活动在大部分活动轨迹中均有出现，对流程模型具有较大的影响，执行流程模型的过程中很大概率会遇到该活动。

(1)

与活动重要程度相关的另一个因素就是活动的频率。将活动对流程模型的影响程度与活动的频率相结合进行计算即可得到活动对流程模型的重要程度，具体计算方法如式(2)所示。在日志数据中，较大的活动频率可能比较小的活动频率大很多倍，直接将活动的频率与影响因子相乘作为重要程度可能不够准确。为解决这个问题，这里对频率值取log处理，使数据有区分度且差别又不那么大，然后再做归一化处理，将其转化为[0,1]内的数值。例如，给定两个重要程度比较接近的活动A、B，且f(A)=1 000f(B)，此时使用log函数对其进行处理可以非常好地将巨大的数量级差距缩小为倍数级，降低频率倍数差别过大的影响。

(2)

活动关系重要程度的计算方式与活动重要程度类似，也是需要计算活动关系的频率及其对流程模型的影响程度，具体计算方式如式(3)-式(4)所示。活动关系对流程模型的影响程度用g(A,B)进行表示，与两端活动的重要程度相关。在大多数条件下，两端活动的重要程度对活动关系的重要程度同等重要，因此直接计算它们的平均值即可。活动关系的频率f(A,B)也是参照活动处理方式进行归一化处理，然后与活动关系对流程模型的影响程度g(A,B)相乘即可得到活动重要程度sig(A,B)。

(3)

(4)

3.2 自动化参数配置方法的实现

自动化参数配置方法的实现主要分为两个部分，分别是活动重要程度的配置以及活动关系重要程度的配置。在配置活动重要程度时，首先根据日志数据获取对应的活动轨迹数据，然后根据活动轨迹数据计算活动的频率以及活动对流程模型的影响程度，最后按照式(2)将活动频率与活动对流程模型的影响程度相结合计算得到活动重要程度参数，如算法1所示。

算法1活动重要程度配置算法

Input: TraceSet;

//根据流程日志数据得到的活动轨迹

Output: sig(A);

//活动重要程度

Method:

1 Procedure map(TraceSet)

2 foreach trace in TraceSet do

3 total+=|trace|

4 foreach A in trace do

5 counts(A)+=1

6 gs(A)=1

7 foreach A in ActivitySet do

8 count(A)+=counts(A)

9 g(A)+=gs(A)

10 foreach A in Activity do

11 Output(A, count(A), g(A), total)

12 Procedure reduce(key, CountIterator, GIterator, totalIterator)

13 foreach countItem in CountIterator

14 count(A)+=countItem

15 foreach gItem in GIterator

16 g(A)+=gItem

17 foreach totalItem in totalIterator

18 total+=totalItem

19 f(A)=count(A)/total

20 output(f(A), g(A))

21 max=0;

22 foreach A in ActivitySet

23 if f(A)>max then max=f(A)

24 foreach A in ActivitySet

25 sig(A)=logf(A)/logmax*g(A)

算法1展示了活动重要程度配置过程的伪代码，输入数据为根据日志数据得到的活动轨迹数据，输出为数据中涉及到的每个活动对应的重要程度数值。算法的1-20行是一个mapreduce任务，该任务的map阶段遍历活动轨迹，统计每条活动轨迹中各个活动的出现次数，然后在reduce阶段对每个活动分别进行处理，计算其频率f(A)以及对流程模型影响程度函数g(A)。在算法的21-25行将数据进行整合处理，计算每个活动的重要程度。

活动关系重要程度的实现与其相似，也是通过一个mapreduce任务完成活动关系频率的计算，然后按照式(4)计算每个活动关系的重要程度参数，具体过程此处不再赘述。

4 流程模型的构建

为了提高流程模型的精准程度，APFM算法在流程模型的构建方面进行了优化，首先从整体、局部两方面综合考虑完成活动关系的处理，然后通过一种自底向上的方法完成活动的抽象与聚合，最后通过计算长距离依赖因子挖掘流程模型中的长距离依赖关系。下面分别对这三个部分进行具体描述。

4.1 活动关系的处理

活动关系的处理包括活动关系的过滤以及活动逻辑关系的识别。活动关系的过滤是从宏观角度对活动关系的重要程度进行分析，并结合活动相关度对活动关系进行过滤，去除重要程度较低的活动关系。活动逻辑关系的识别是从局部角度，对活动关系在局部范围内的重要程度进行分析，以此为基础识别活动之间的逻辑关系，该步骤中也对部分活动关系进行过滤。

定义活动相关度cor用以描述表示在流程模型中两个活动之间的关系是否紧密，具体的计算方式如式(5)所示。给定活动A、B，如果在日志数据中，两个活动经常一前一后同时出现，且活动关系(A，B)在活动A、活动B各自的关系中占有比较大的比重，那么可以认为两个活动之间的相关度较高；反之则认为两个活动的相关度较低，相关的数据可能为噪声数据。

(5)

定义util值[6]进行活动关系的过滤，util值的计算方式如式(6)所示，util值与活动重要程度、活动相关度有关，通过一个系数α调整活动重要程度与活动相关度的权重比例。在具体进行活动关系的过滤时，需要指定一个阈值rc，如果某条活动关系的util大于等于阈值rc，那么保留该条活动关系，否则直接过滤即可。

util(A,B)=α×sig(A,B)+(1-α)×cor(A,B)

(6)

定义活动关系的相对重要程度rel[6]，用来表述该活动关系在局部范围内的重要程度，以此为基础进行活动逻辑关系的识别，其具体计算方式如式(7)所示。给定活动A、B识别其逻辑关系，如果rel(A,B)和rel(B,A)都超过预设的循环因子lf，那么两个活动可能形成了一个长度为2的环；否则，如果rel(A，B)和rel(B,A)差值大于预设的并行因子cf，那么说明其中一个比较重要，另一个可能为噪声数据产生，保留rel值较大的关系，将rel值较小的关系去除。如果rel(A,B)或rel(B,A)有一个低于lf，且两者差值小于cf，说明两个活动可能为并行关系，活动之间并不存在依赖关系。

(7)

算法2展示了活动关系处理过程的伪代码，输入数据为OldRelationSet，表示直接根据活动轨迹得到的、未经过处理的活动关系集合，输出为流程模型的活动关系集合RelationSet，包括循环结构关系、直接依赖关系以及并行关系。算法的4-8行进行活动关系的过滤，将保留下来的活动关系保存在NewRelationSet中。算法的9-15行进行活动逻辑关系的识别，遍历NewRelationSet中的每个活动关系，计算其相对重要程度进而识别两个活动的逻辑关系，分别保存在L2Set、SDSet以及PSet中。最后将这三个集合进行整合得到流程模型的活动关系集合。

算法2活动关系处理算法

Input: OldRelationSet;

Output: RelationSet;

//流程模型的活动关系集合

L2Set;

//长度为2的循环结构集合

SDSet;

//直接依赖关系集合

PSet;

//并行关系集合

Method:

1 Calc(SumCountInSet, SumCountOutSet);

2 Calc(SumSigInSet, SumSigOutSet);

3 Init(NewRelaionSet);

4 for (A,B) in RelationSet do

5 Calc(cor(A,B))

6 Calc(util(A,B))

7 If (util(A,B)>rc) then

8 NewRelationSet=NewRelationSet∪(A,B)

9 for (A,B) in NewRelationSet do

10 Calc(rel(A,B), rel(B,A));

11 if (rel(A,B)>lf && rel(A,B)>lf) then

12 L2Set=L2Set∪(A,B)

13 else if (abs(rel(A,B)-rel(B,A))>cf) then

14 SDSet=SDset∪(A,B)

15 else PSet=PSet∪(A,B)

16 RelationSet=L2Set∪SDSet∪PSet

4.2 活动的抽象与聚合

APFM算法通过一种自底向上的方法完成活动的抽象与聚合，该方法的处理思想借鉴了自底向上层次聚类算法的处理思想，首先根据预先设置阈值ac完成活动的筛选。然后遍历每个需要处理的活动进行抽象处理，判断该活动是否能够与其他活动进行聚合操作。最终流程模型的活动集合分为两个部分，一部分为重要程度较高、不需要进行处理的活动，另一部分则是完成抽象与聚合操作后得到的抽象活动集合。

活动抽象与聚合处理的具体过程通过算法3描述的伪代码进行详细描述，该步骤的输入数据为活动关系集合以及直接根据日志数据得到的活动集合，输出数据为流程模型的活动集合。算法的3-6行完成活动的筛选，将重要程度较低的活动识别出来并加入tempActivitySet中，重要程度较高的活动直接加入ActivitySet中。算法的7-8行是为tempActivitySet中的每个活动计算其关系编码。活动的关系编码是判断两个活动是否能够进行聚合操作的依据，由活动是否与其他重要程度相连的二进制字符串来表示，如果两个活动的关系编码相同，那么说明它们同时与某个重要程度较高的活动相连，不能进行聚合操作。使用活动的关系编码进行判断处理，可以降低算法的复杂度，提高数据处理效率。算法的9-18行是活动抽象与聚合的核心部分，通过一个循环完成。每次从tempActivitySet中取出一个抽象活动A，遍历与其相连的其他抽象活动B，根据活动关系编码判断B是否能够与A进行聚合操作。如果可以，这将抽象活动B加入抽象活动A对应的抽象活动集合中，更新抽象活动A的活动关系编码以及关联关系，并将抽象活动B从tempActivitySet中移除，表示已完成对抽象活动B的处理，当抽象活动A的聚合操作完成之后，将其加入AbstractSet中。当tempActivitySet中的所有抽象活动都被处理完成之后，再将AbstractSet加入ActivitySet中，得到流程模型的活动集合。

算法3活动的抽象与聚合处理算法

Input: RelationSet;

//活动关系集合

OldActivitySet;

//根据日志数据得到的活动集合

Output: ActivitySet;

//活动集合

AbstractSet;

//抽象后得到的活动集合

Method:

1 Init(tempActivitySet);

2 Init(MarkList);

3 foreach A in OldActivitySet do

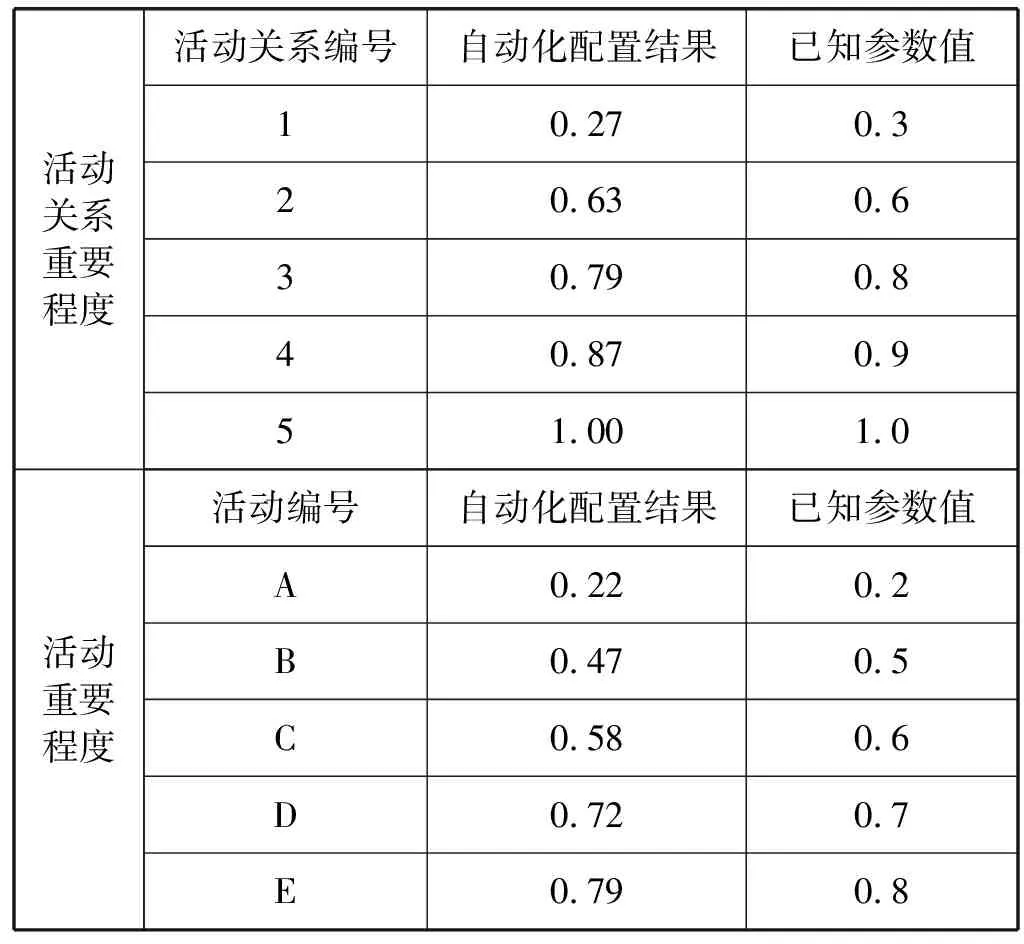
4 if (sig(A)

5 tempActivitySet=tempActivitySet∪A;

6 else ActivitySet=ActivitySet∪A;

7 foreach A in tempActivitySet do

8 Calc(MarkList(A));

9 while (!tempActivitySet.empty()) do

10 A=tempActivitySet.get();

11 Mark=MarkList(A);

12 SubRelationSet=A.relation;

13 foreach B in SubRelationSet do

14 if (Mark.hasSameBit(MarkList(B))) then

15 tempActivitySet.remove(B);

16 update(Mark,B);

17 update(SubRelationSet,B);

18 AbstractSet=AbstractSet∪A;

19 ActivitySet=ActivitySet∪AbstractSet;

4.3 长距离依赖关系的处理

长距离依赖关系是指给定流程模型，存在活动A、活动B与活动C、活动D，活动C的执行依赖于活动A的执行，活动D的执行依赖于活动B的执行。传统的模糊挖掘算法在建模过程中并未针对长距离依赖关系给出合理的解决方案，本文提出的APFM算法对活动轨迹进行分析，通过计算长距离依赖因子挖掘流程模型中的长距离依赖关系。

长距离依赖因子的具体计算方式如式(8)所示。为了便于描述，定义活动的选择状态，该状态是指在流程模型中，在执行活动之前有一个中间状态，如果后续可以执行的活动不唯一，可以任意选择，那么当前的中间状态就是活动选择状态。给定活动A、B，如果两个活动具有长距离依赖关系的话，那么它们的前一个状态一定都是活动选择状态，而且在选择执行后续的活动时，分别选择执行活动A和活动B，由此可以定义长距离依赖因子，用来描述两个活动是否具有长距离依赖关系。给定两个活动A、B，S1、S2分别是它们对应的活动选择状态，如果S1选择执行活动A，S2选择执行活动B的情况在所有情况中所占比例较高，大于预设的阈值lc，则可以判定两个活动具有长距离依赖关系。

(8)

算法4展示了挖掘长距离依赖关系的具体过程。算法的1-9行是一个mapreduce任务，该任务可以根据活动关系构建活动依赖关系网络。根据活动依赖关系网络可以非常轻松地找出每个活动的依赖关系，判断其前一个状态是否为活动选择状态。算法的10-16行完成长距离依赖关系的挖掘，对于每个活动，判断与其他活动是否具有长距离依赖关系，如果是则将其加入LongRelationSet中。

算法4长距离依赖关系挖掘算法

Input: RelationSet;

//活动关系集合

ActivitySet;

//活动集合

Output: LongRelationSet;

//长距离依赖关系集合

Method:

1 Procedure map(RelationSet)

2 foreach (A,B) in RelationSet do

3 Output(A, in, B);

4 Output(B, out, A);

5 Procedure reduce(key, mode, value)

6 if (mode==in) then

7 succMap.Count(value).add(1);

8 else preMap.Count(value).add(1);

9 output(key, preMap, succMap);

10 foreach A in ActivitySet do:

11 if (A.getPreState()!=SelectionState) then

12 continue;

13 foreach B in ActivitySet do:

14 if (A.getPreState()!=SelectionState) then

15 continue;

16 Calc(ldr(A,B));

17 if (ldr(A,B)>lf) then

18 update(LongRelationSet,(A,B));

5 实 验

实验分为自动化参数配置实验、算法性能分析、算法运行结果分析三个部分，分别对APFM算法三个方面优化是否达到预期效果进行分析，从而对APFM算法进行比较全面的评估。实验使用的数据为某高校网络课程平台的用户学习日志数据，整个数据集包含大约8 498万条数据，涉及37门网络课程，数据中的每条记录均包含用户学号、用户所选课程、所学的课程章节以及时间等信息。实验过程中，需要根据课程编号提取某门课程相关的数据进行分析。

5.1 自动化参数配置实验分析

为了评估APFM算法中自动化参数配置方法的有效性，实验选择活动重要程度、活动关系重要程度已知的数据集使用自动化参数配置方法进行处理，将自动化配置结果与已知的数据参数值进行对比，判断它们的差值是否在合理范围内。

表1展示了使用APFM算法中自动化参数配置得到的参数值以及数据原有参数值对比的部分结果。表1选取5个活动以及5对活动关系，对比自动化配置结果以及已知的参数值可以看出，对于任意一对数据，两者的差值均不大于0.05，处于合理误差范围之内。对于表1中未展示的、数据集中包含的数据，数据差值也在合理范围内，由此证明自动化参数配置方法可以非常好地完成参数配置的任务。

表1 自动化参数方法结果对照表

5.2 APFM算法的性能分析

在进行性能分析实验时，实验环境为包含2个数据处理节点的hadoop集群，每台机器的配置为CPU i5- 4460T，4核8线程，内存为8 GB，操作系统为ubuntu 18.04，64位操作系统。实验选择单机版的模糊挖掘算法、并行化的启发式挖掘算法进行对照，构建了日志条数分别为103至106数据规模大小不同的数据集，对比不同算法在处理不同规模数据集时的运行时间。

图2展示了不同算法运行时间的对比结果，其中纵坐标为时间(ms)，横坐标为所使用的数据集的数据规模。与单机版的传统模糊挖掘算法相比，当日志数据规模比较小时，APFM算法的运行时间较长，当数据规模较大时，APFM算法的运行效率渐渐高于单机版模糊挖掘算法，而且数据规模越大，APFM算法的优势越明显。尽管并行化的启发式挖掘算法在处理不同规模数据集时表现都不错，数据处理耗时均低于单机版的模糊挖掘算法，但当数据规模达到50万甚至更大时，APFM算法数据处理效率更具优势。由此可以得出结论，APFM算法具备较好的处理大规模数据集能力，表现优于单机版的模糊挖掘算法以及并行化的启发式挖掘算法，符合预期的优化目的。

图2 与单机版算法运行时间对比图

为了更进一步分析APFM算法的运行性能，统计APFM算法在不同处理不同规模数据集时各个步骤运行时间，以便分析APFM算法的瓶颈。图3展示了APFM算法运行过程中各个阶段耗时的对比图，横坐标为所使用的数据集中数据规模，纵坐标为将运行时间取log的值。由于不同阶段的运行时间差别较大，需要将运行时间取log后便于观察。可以看出，APFM算法最耗时的部分为自动化参数配置，而其余三个建模过程耗时很少。这是由于自动化参数配置阶段通过执行mapreduce任务完成整个数据集的处理，该过程复杂度较高，需要遍历整个数据集完成参数配置，是一个比较耗时的过程。而其余三个数据处理过程复杂度不高，只与活动总数、活动关系总数相关，因此耗时很短。由此可以得出结论，APFM算法的瓶颈在于自动化参数配置阶段对整个数据集处理，其他阶段耗时很短。APFM算法数据处理方式的特点在于只需要在自动化参数配置阶段，对整个数据集处理一次，完成数据集的简化，后续过程中需要根据简化后的数据进行处理即可得到流程模型。当数据集规模较小时，这种数据处理方法效率不高，但当数据集的规模较大时，这种数据处理方法的优势就逐渐体现出来。

图3 APFM算法不同阶段运行时间

5.3 APFM算法的运行结果分析

为了验证APFM算法的有效性，对APFM算法的运行结果进行比较客观、全面的分析，实验选择两组数据分别使用APFM算法进行建模分析。第一组实验数据为用户参与网络课程《办公自动化》的学习行为日志数据，该数据集包含275 153条日志记录，处理后得到了17 343条活动轨迹。第二组实验数据为用户参与网络课程《公关与社交礼仪》的学习行为日志数据，该数据集包含267 682条日志记录，处理后得到了9 730条活动轨迹。使用APFM算法进行处理时，将阈值rc、ac、lc均设置为0.8。

图4展示了使用APFM算法得到的流程模型的可视化结果，其中，长方形节点表示日志中包含的活动，六边形节点表示对部分重要程度较低的活动进行聚合与抽象后得到的抽象活动集合节点。为了便于表示，每个活动节点、抽象活动集合节点都用字母表示。实线箭头表示简单的依赖关系，虚线箭头表示长距离依赖关系。整体来看，这两个流程模型结构清晰，不包含冗余的活动关系，准确地挖掘出了长距离依赖关系之后，整个流程模型也显得更加完整。为了对以上流程模型进行更加透彻的评估分析，根据文献[20]提出的流程模型的评价指标，分别计算它们的可重现性、简洁性、精确性以及通用性4个指标并进行分析。

图4 流程模型示意图

实验选择了传统的模糊挖掘算法以及启发式挖掘算法进行对照，将这两个算法运行得到的流程模型与APFM算法得到的流程模型进行对比，具体的评估指标计算结果如表2所示，然后分别对每个指标进行分析：

(1) 可重现性：APFM算法得到的流程模型可重现性较传统的模糊挖掘算法有一定的提升，但两者均不如启发式挖掘算法，这是由于它们在建模过程中对某些活动进行了抽象与聚合操作，导致流程模型并不能够精确地还原活动轨迹中的每一个活动，只能还原部分重要程度较高的活动。

(2) 简洁性：APFM算法继承了模糊挖掘算法的优点，得到流程模型结构层次比较清晰，活动关系也比较简洁，不存在冗余的活动关系，挖掘得到的长距离依赖关系也能够比较清楚地展现出来。因此APFM算法得到的流程模型简洁性非常好。

(3) 精确性：APFM算法得到的流程模型结构比较简洁，未出现过拟合问题，其精确性比启发式挖掘算法更好。APFM算法在建模过程中进行了优化，添加了长距离依赖关系的处理方法，确保得到的流程模型更加贴近日志数据中描述的行为，极少出现日志数据描述之外的行为。

(4) 通用性：APFM算法得到的流程模型通用性也是最好，也是得益于APFM算法保留了传统模糊挖掘算法的优势以及对建模方法的进一步优化，保证得到的流程模型更加符合日志数据描述的行为，对未来可能出现的执行实例能够进行比较精确的预测。

表2 流程模型评价表

综合来看，APFM算法得到的流程模型简洁性非常好，精确性、通用性较传统的模糊挖掘算法相比均有一定的提升。但受限于算法本身的建模思路，导致流程模型的可重现性一般。因此，在可重现性要求不是非常苛刻的条件下，使用APFM算法处理日志数据可以得到比较精确的流程模型。

6 结 语

模糊挖掘算法是流程挖掘中常用的算法之一，但该算法存在一些缺陷，本文通过对这些缺陷进行分析并进行改进，提出了一种自适应的并行化模糊挖掘算法。APFM算法可以进行参数的自动化配置，使用起来更加简单；通过并行化方法完成数据处理，增强了处理大规模数据的能力；对建模过程进行优化，添加了长距离依赖关系的处理方法，使整个建模过程更加细致、全面，确保得到的流程模型更加精确。实验证明，APFM算法对传统模糊挖掘算法不足之处的优化均达到了预期的效果。

综合目前流程挖掘算法优化方面的研究来看，模糊挖掘算法应用方面的研究较多，但算法优化方面的研究很少，本文对于模糊挖掘算法的优化是比较新的研究方向。尽管本文提出的APFM算法在一定程度上取得了不错的结果，但还需要在更多其他的应用场景中对其进行实验，尝试挖掘其不足之处。在算法的优化方面，除了提高算法在大规模数据集的处理能力，还可以尝试对算法的处理思路、实际应用场景的特点进行分析，提出更好地解决方案。