基于Lab颜色空间的融合改进二进制量子PSO和Otsu优化算法
2022-07-12唐文权
徐 武 文 聪 唐文权 郭 兴
(云南民族大学电气信息工程学院 云南 昆明 650500)
0 引 言
图像分割是根据图像特征提取和分离出目标图像和背景的技术。目前,彩色图像的分割方法可以大致分为4类:基于阈值的分割算法、基于图像区域的分割算法、基于聚类的分割算法,以及利用特定理论的分割算法。大津法(Otsu)是基于阈值分割的图像分割算法,依据二维直方图选取阈值,通过计算图像中目标和背景之间的最大类间方差得到分割阈值[1]。虽然Otsu算法已经被广泛应用,但也存在着计算量大、实时性差等缺点。
针对上述Otsu算法的缺点,为了提升阈值分割速度,得到最佳阈值,常用一些算法来优化,文献[2]融合了二阶振荡粒子群算法和Otsu算法,但随着阶数的增加程序运行时间会变长;文献[3]在HSV颜色空间中融合了改进ω的粒子群算法和Otsu算法,但是不利于小目标图像的分割;文献[4]将改进的人群搜索算法(WFSOA)融合到二维Otsu算法中,但是对于背景对比不明显的灰度图像分割效果欠佳。
通过分析以上算法,本文提出一种在Lab空间中融合改进二进制量子粒子群(BQPSO)和改进二维Otsu的图像分割算法。首先将图像的颜色空间转换为Lab颜色空间,改善RGB空间中3种颜色分量间高度线性相关的问题;BQPSO全局搜索能力强、搜索范围能覆盖整个可行解空间、全局效果好,而且对于离散空间的搜索效果也很好,因此被广泛应用于多目标优化的场景中[5]。本文对BQPSO中的不同粒子的权重做了改进,进一步提高了粒子的多样性和算法的收敛速度。对于二维Otsu算法,本文通过划分图像空间,对图像的中心区域做侧重运算,改进了最优阈值计算策略,提升了算法的快速性。最后,将二进制量子粒子群优化算法搜索到的最优阈值作为Otsu算法的分割阈值完成对图像的分割。
1 Lab颜色空间的转换
由于RGB空间各个颜色分量高度线性相关,空间色彩分布不匀的缺陷会对图像分割结果产生影响,而Lab颜色空间具有很强的精确性、稳定性,因此将Lab空间应用于图像分割,选择最适于分割的分量,就能取得最好的目标,背景分离效果[6]。
Lab空间包含a和b两个颜色通道以及亮度通道L[7]。当a或b的取值越高时,则表示具有更多的红色或黄色比率,而取值越低则表示具有更多的绿色或蓝色的比率。
RGB模式转换到Lab色彩模式,需要借助过渡通道XYZ颜色空间[8]。转换式如下:

(1)
然后转换到Lab空间:
L=116f(Y)-16
a=500f(X-Y)
b=200(Y-Z)
(2)
(3)
依据式(2)和式(3)可以将图像从RGB颜色空间转换到Lab颜色空间。
2 二进制量子粒子群算法及其改进
针对粒子群优化算法中粒子无法覆盖整个搜索空间的缺陷,文献[9]提出了一种具有量子运动特征的粒子群优化算法(QPSO)。与粒子群算法相比,QPSO只有一个位移修正公式,简化了程序的复杂度,而且能收敛到全局最优解[10]。但是QPSO主要针对实数解空间,对于离散空间的求解没有很好的效果,而二进制量子粒子群算法(BQPSO)对以上问题有良好的处理效果[11]。
在QPSO中,由一个参数就能表示粒子的位置信息和速度:
pi=φ×pbesti+(1-φ)×gbest
(4)
(5)
(6)
式中:φ和u是(0,1)之间的随机数;Pi为局部吸引子;mbest为中值最优位置;x(t)为粒子的相关位置信息;M是粒子总数目[12]。
BQPSO的算法思想与QPSO基本一致,只是将粒子的位置由二进制数表示。所以,可以从QPSO算法方程得到BQPSO算法方程。式(7)表示用海明距离代表两个粒子位置的差值[13]:
|X-Y|=dH(X,Y)
(7)
针对传统的BQPSO中mbest计算方式对每个粒子赋予的权重是相同的,很难突出最优粒子的优点,本文做了如下改进:利用加权更新改进mbest(t)的计算公式,将式(5)中ω改为权重系数ωi:
(8)
式中:f(Pi(t))为最优适应度。平均最佳位置mbest的更新公式如下:
(9)
从式(9)可以看出,在计算BQPSO的平均最优位置时,提高了最优粒子在种群中的权重,因而提高了种群粒子多样性,最终使收敛速度提高。
3 二维Otsu分割算法及其改进
二维Otsu算法同时考虑了各个像素的灰度信息及位置信息,能够避免光照、噪声的干扰作用[14]。
背景类B、目标类T阈值出现的概率分别为:
(10)
则整幅图像的灰度级向量u是:
(11)
同理可求出背景类、目标类的均值向量uB、uT。
目标、背景间的离散测度为:
S(s,t)=PB×(uB-u)×(uB-u)T+
PT×(uT-u)×(uT-u)T
(12)
离散测度和分割效果呈正相关,离散测度最大时的阈值表示为:
tr(S(s*,t*))=max(tr(S(s,t)))=
PB×[(uBi-ui)2+(uBj-uj)2]+
PT×[(uTi-ui)2+(uTj-uj)2]
(13)
传统方法是将图像分为t-1个灰度区间,且对全部图像寻找最佳阈值,但是一般图像的检测目标出现在中部区域附近[15]。因此,本文对图像的区域划分方法做了如下改进:通过侧重计算图像中心区域像素灰度值和邻域灰度值的平均值来寻找最佳阈值,可以在不牺牲分割效果的前提下,大大减少运算时间,提高图像阈值分割效率。
图像的大小为M×N,分割阈值为t,则背景部分的灰度级向量表示为:
μb=(μbi,μbj)=
(14)
目标部分的灰度级向量表示为:
μo=(μoi,μoj)=
(15)
因此,对式(11)可改进为:
μ=(μi,μj)=

(16)
4 改进的Otsu图像分割算法
本文将二进制量子粒子群优化算法应用于Otsu优化算法中,提出改进的二进制量子粒子群-Otsu图像分割算法。利用二进制数代表粒子的位置,用海明距离表示粒子之间的距离,然后计算mbest,通过多次迭代,获取最佳阈值。本文改进的二进制量子粒子群算法在精度和收敛速度等方面相对于粒子群算法得到了很大的加强。
本文算法步骤如下:
步骤1将待分割图像的颜色空间由RGB转换为Lab;
步骤2用二进制表示群体中的每个粒子的初始位置,并初始化粒子当前位置,即令Pi(0)=Xi(0);
步骤3计算对角线区域灰度级梯度二维直方图;
步骤4计算每个粒子的适应值,当f(xi(t)) 步骤5根据公式计算mbest; 步骤6计算全局最优粒子Pg(t); 步骤7计算局部吸引子PPi; 步骤8对PPi进行变异,重新生成粒子群; 步骤9当迭代次数达到设定值,转到步骤10,若算法没有达到则转到步骤4; 步骤10确定搜索到的最佳阈值; 步骤11将最佳阈值作为图像的分割参考阈值,对Lab颜色空间的图像进行分割。 融合二进制量子PSO和Otsu优化算法流程如图1所示。 图1 改进二进制量子PSO+Otsu算法流程 仿真实验分别采用文献[2]算法、文献[3]算法以及本文算法对Lab色彩空间的图像进行分割,为了对比不同算法的快速性,在保证能搜索到最优阈值的前提下尽可能减少算法的迭代次数,从而让算法的运行时间降到最低。仿真结果如图2-图3所示。 (a) 原图 (b) 文献[2]算法 (c) 文献[3]算法 (d) 本文算法图2 室内照片不同算法对比实验结果 (a) 原图 (b) 文献[2]算法 分别对比了不同算法的运行时间、迭代次数以及求得最优解次数,实验结果如表1所示。 表1 图像分割算法对比 可以看出,对于室内照片的图像分割,文献[2]算法的迭代次数是23次,算法运行时间比较长,虽然最终求得的最优解比例较文献[3]高,但迭代次数太多,对实时性的要求难以满足;与文献[2]算法相比,文献[3]算法的迭代次数大大减少,而且算法收敛速度更快,程序运行时间相对减少,但是得到最优解的次数相对较少,一般来说,在小目标图像与背景分割时,文献[3]算法的处理效果不佳。本文算法是在Otsu算法和标准BQPSO的基础上优化的。通过对表1的各项指标综合分析可以看出,文献[2]算法、文献[3]算法和本文算法分割室内复杂背景的运算时间分别为313、260和243 ms,迭代次数分别为23、14和8次,肺部CT图像的运算时间分别为210、176和147 ms,迭代次数分别为19、11和7次,结果表明,在算法迭代次数、程序运行时间这两个方面本文算法具有足够的优势,因此实时性是本文算法的最大优势,而且从分割出图像可以看出,本文算法在噪声去除和目标识别方面突出的优势。综合来看,本文算法多项指标相比另外2种算法有很大的提升,对图像分割有很大的帮助。 本文对复杂背景下的图像分割进行了研究。首先加入了Lab颜色空间变换,然后在传统二维Otsu算法的基础上,提出针对对角线区域搜索最优阈值,最后融合了二进制量子粒子群优化算法,并与基于二阶振荡粒子群优化的Otsu算法和基于HSV颜色空间的改进PSO+Otsu(S)分割算法进行了仿真比较。结果表明,本文提出的算法适用于复杂背景下的图像分割,而且在运行速度、分割精度等方面都优于另外两种算法。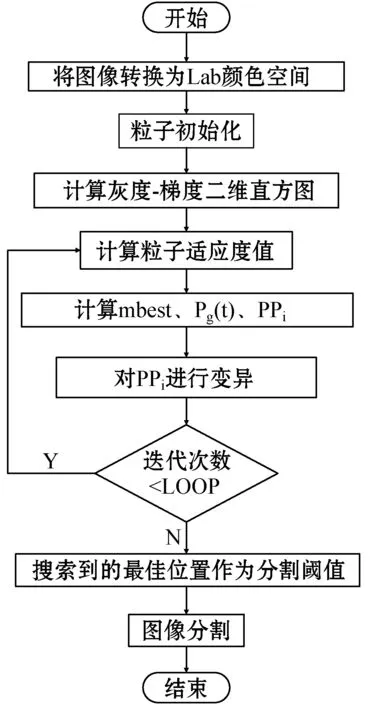
5 实验结果与分析




6 结 语
