图计算中压缩格式对单源最短路径算法影响的特性化分析
2022-07-12邓军勇赵一迪
邓军勇 赵一迪
(西安邮电大学电子工程学院 陕西 西安 710121)
0 引 言
在大数据背景下,物理世界中图数据的规模呈爆炸式增长[1],社交网络分析、网页搜索、推荐系统、生物信息学和网络安全等大量实际应用都紧密依赖于图计算系统[2,4]。当前,面向不同图算法的图计算加速器正蓬勃发展发展,为了使大规模图数据得到更高效的处理,高性能图计算加速器受到了广泛关注。
真实图数据的稀疏性以及分布幂律性导致图计算负载失衡[5],选择合适的图数据表示方式有助于提升图计算性能[6]。图数据格式主要分为Edge Array(边阵列)和Adjacent List(邻接表)两种。以Edge Array的方式存储,可以顺序地读取图数据中边的属性,能有效提高其访存效率[7,9];以Adjacent List方式存储可有效减少随机访问从而提高内存访问速度[10,13]。目前,图计算加速器的设计只考虑了从硬件角度对图数据的优化处理,无法根据具体应用需求来选择最适合的压缩格式,从而无法发挥图计算加速器的最优性能。因此,根据不同的环境及图算法需求选择相应的数据格式使图计算加速器性能最优化显得尤为重要。但是在不同的环境要求下,目前没有适用的标准来决定哪种压缩格式的图数据在什么时候更适合于哪个算法。因此,对于图计算加速器的设计,建立一个性能评价模型来提供相关的性能数据,决定在不同条件应选择的图数据格式成为一种必然趋势。
本文通过对图计算中COO[14]、CSC[15]、CSR[16]、DCSC[17]和CSCI[18]五种图压缩格式分别作为遍历类应用单源最短路径SSSP算法的输入格式进行特性化分析,分析不同数据集下不同压缩格式的性能指标,如 IPC、数据移动量(datamv)、功耗(energy)、各级cacheMPKI、执行时间(exec.time)等,通过对这些特征数据的比较为不同需求图计算加速器的设计提供依据。
1 算法及压缩格式分析
1.1 SSSP算法
单源最短路径算法[20]是计算从源点到所有其余顶点的路径上边权值之和的最小值的算法,在实际生产和生活中的应用非常广泛,是网络理论、地图路径查询和线路安排等许多实际问题选择最优解决方案的基础。
SSSP算法的基本思想为:若s为源顶点,u为某次迭代的活动顶点,那么则在与u相连的顶点中依次选择未访问顶点vi(state[vi]=0)入列以便作为活动顶点顺序访问,同时计算其当前路径长度为源顶点到当前活动顶点的路径长度dis(u)加该顶点的权值weight(vi)得到temp(vi);若某一顶点被多次作为相连顶点访问(state[vi]=1),则每次都计算其当前路径长度temp(vi)并与dis(vi)进行比较,选择两者最小值作为dis(vi)进行下次迭代,直至队列为空。其伪代码如表1所示。
算法1SSSP算法伪代码
inputGraphG(V,E);源顶点s;(u,v)边的权值weight(u,v)
output 从源顶点s到其他各个顶点的最短路径长度min[n]

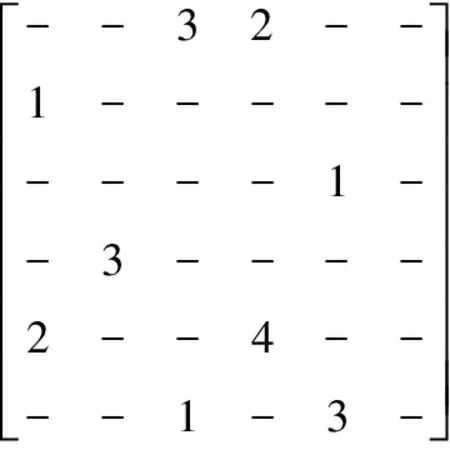
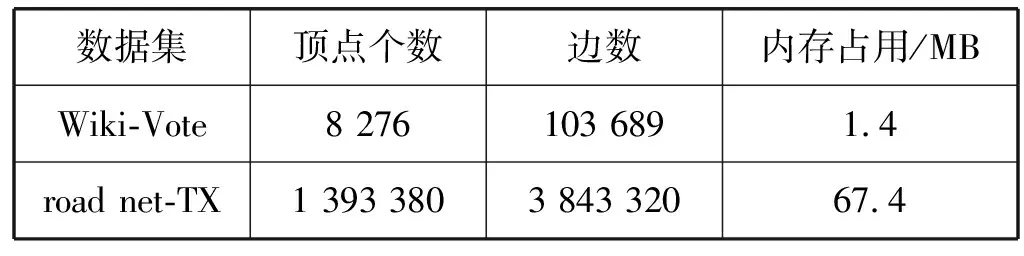
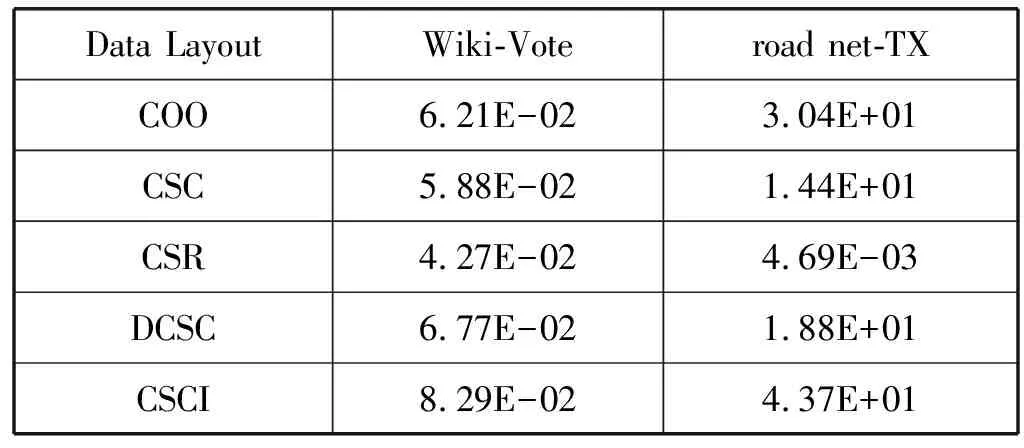
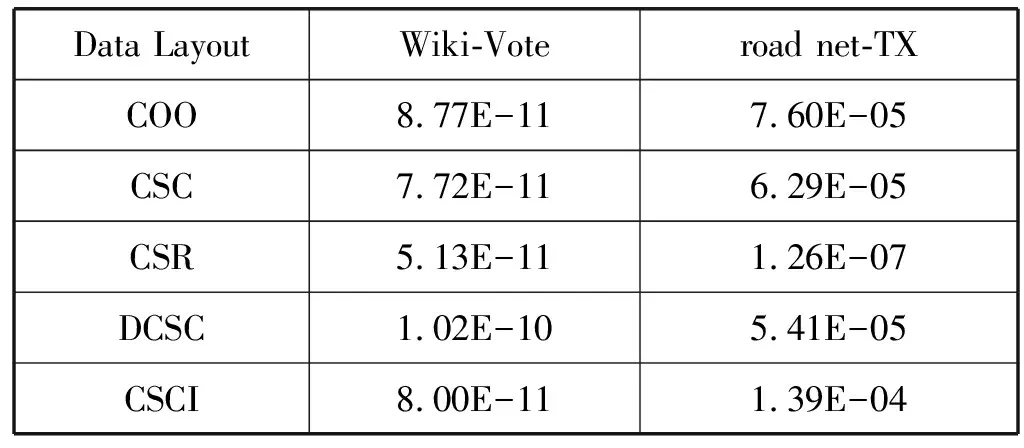
a)b)c)d)e)f)g)h)i)j)k)l)m)n)o)p)forn∈Vdo//初始化 dis[n]=INF;//源顶点s到顶点n的当前路径长度 min[n]=INF; state[n]=0;//顶点n的活动状态dis[s]=0;state[s]=1;queue←s;//源顶点s入队while(P.queue不为空) do forn(n为s的邻接点) do ifstate[n]=0 P.queue←n; state[n]=1; dis[n]=dis[s]+weight(s,n); ifdis[n] (1) COO压缩格式。在COO(Coordinate)按坐标表示,每一个元素需要用一个三元组(行号,列号,数值)来表示。这种压缩方式比较简单,每个三元组都可以直接定位,但是记录的信息多,因此占用空间较大[14]。如图1所示的原始矩阵,其COO压缩格式为(0,2,3),(0,3,2),(1,0,1),以此类推。 图1 原始矩阵 (2) CSC压缩格式。CSC(Compressed Sparse Column)按列压缩,需要三个数组表达:列偏移、列号和数值。其中数值和行号与COO一致,表示一个元素以及其行号,列偏移表示某一列的第一个元素在values里面的起始偏移位置(即该元素所在当前列之前的非零元素个数)[15]。图1中,第一列元素1是0偏移,第二列元素3是2偏移,第三列元素3是3偏移,以此类推,在列偏移的最后补上矩阵总的元素个数。 (3) CSR压缩格式。CSR(Compressed Sparse Row)按行压缩,与CSC相似,也需要三个数组来表达:行偏移、列号和数值。数值和列号与COO一致,表示一个元素以及其列号,行偏移表示某一行的第一个元素在values里面的起始偏移位置(即该元素所在当前行之前的非零元素个数)[16]。图1中,第一行元素3是0偏移,第二行元素1是2偏移,第三行元素1是3偏移,以此类推,在行偏移的最后补上矩阵总的元素个数,本例中是9。 (4) DCSC压缩格式。如表1所示,DCSC(Doubly Compressed Sparse Column)双压缩稀疏列主要使用四个数组来存储给定的矩阵,一个数组用于存储至少具有一个非零元素的列的列索引,以及指向与该列索引相对应的行索引在上述数组中开始的位置,以及非零元素所在行索引和数值[17-18]。 表1 原始矩阵的DCSC压缩 (5) CSCI压缩格式。CSCI(Compressed Sparse Column Independently)独立稀疏列压缩,对稀疏邻接矩阵按列独立压缩成一个个的数据对(ioc,index, value),ioc为“1”,则表示index为列号,value表示该列非零元素的个数;若ioc为“0”,则表示index为当前列非零元素所在的行号,value表示该非零元素的值[19]。图1中,压缩结果为(1,0,2),(0,1,1),(0,4,2),(1,1,1),以此类推。 本次实验是在4核8线程Intel(R) Core(TM) i5- 8250U CPU上运行的,其中CPU具有6 MB的三级缓存,该CPU以1.6 GHz的时钟频率运行,平台具有8 GB内存和1 TB外存,并运行Linux内核4.15.0系统,所有代码均使用gcc 5.4.0版本进行编译和运行。 实验数据选自斯坦福大学的SNAP(Stanford Network Analysis Project)数据集中road network的road net-TX[21]以及social network的Wiki-Vote[22],其顶点个数、边数以及内存占用情况如表2所示。 表2 实验所选的数据集 perf是内置于Linux内核源码树中的性能剖析(profiling)工具。它基于事件采样原理,以性能事件为基础,对处理器相关性能指标与操作系统相关性能指标进行性能剖析。本文通过分析器收集性能指标数据来计算不同数据集中不同压缩格式的IPC、数据移动量、功耗、计算量、L1、L2以及L3数据缓存MPKI。 根据统计的硬件性能事件,本文分析的性能指标如下:IPC、数据移动量、功耗、计算量、L1、L2以及L3数据缓存MPKI。由于输入图数据规模差别较大,本文将性能指标统一到每一条边的处理上。 (1) 执行时间。任务的执行时间即目标任务真正占用处理器的时间,单位为ms/edgs。根据下式计算三种实现方式在不同压缩格式中的每条边的执行时间: (1) (2) IPC。IPC(Instruction Per Clock)是一个基本性能指标,表示平均每一时钟周期所执行的指令数。一般而言IPC越大越好,说明程序充分利用了处理器的特征。可根据下式计算算法设计的IPC: (2) (3) 数据移动量。数据移动量受延迟和带宽的限制,在高性能计算程序中往往属于不可并行或者很难并行的部分。为了描述数据移动问题,本文在每种SSSP算法实现中记录每条边的数据移动量。通过统计的性能事件,根据下式可计算出在不同压缩格式中的每条边的数据移动量: (3) 式中:Nload和Nstore为加载和存储指令总数,用来表示数据移动,Nedges为边的总数。 (4) 功耗。功耗是图计算加速器的重要性能指标。可根据下式计算每条边的功耗: (4) 式中:Rpower_all为消耗的总能量。 (5) MPKI。MPK(Misses Per Kilo Instructions)是一个用来分析cache性能的通用指标,表示每千条指令的平均未命中数。可根据下式计算各级cache的MPKI: (5) (6) 计算量。分析运行时间对于算法分析也极为重要。在影响程序运行时间的因素中,除了某些超出所有理论模型范畴的因素诸如所使用的编译器和计算器之外,主要的影响因素是所使用的算法和对该算法的输入。可根据下式来计算每条边的执行时间: (6) 本节介绍了在所选的五种压缩格式的内存占用情况以及在SSSP应用下性能特征,并通过性能比较列出了一些图计算加速器设计建议。 图2表示了两种数据集在不同压缩格式下的内存占用情况。可以看出,除COO外的四种压缩格式都对原始数据进行了不同程度的压缩,其中DCSC压缩格式对数据的压缩程度最大,CSCI压缩程度较小,CSR与CSC的压缩结果最明显且二者相差不大。这是因为DCSC在CSC的基础上对列偏移量再次进行压缩,只存储非零元素个数大于等于1的列,所以对于足够稀疏的图数据来说存储效率最高;CSC和CSR两种压缩格式需要每个顶点所有边的个数、边的源顶点(CSC)或者目标顶点(CSR)以及边的权值三个数组来存储图数据,当稀疏矩阵的行列数趋近于相同时,内存占用大小也相近;CSCI压缩格式将稀疏矩阵中列号及该列的非零元素个数、非零元素所在的行号以及属性值都对应存储,而不是只存储非零元素个数、行号及属性值,即会占用更大的内存空间;COO压缩格式是将所有边的信息以最直接的方式存储成三元组的形式,即与数据的原始存储格式相同,内存占用最大。 图2 两种数据集五种压缩格式下的内存占用情况(归一化到COO格式) 为了对不同压缩格式的相同算法处理的性能特征进行系统性的分析,本文通过雷达图的形式显示了COO、CSC、CSR、DCSC以及CSCI五种压缩格式在SSSP应用算法中的性能,如图3所示,在每一幅图中,包括每个压缩格式实现的IPC、数据移动量、执行时间、功耗以及L1、L2和L3三级数据缓存MPKI。其中,每个度量标准的最大值视为100%,其他数据以它作为标准。 (a) 数据集Wiki-vote (b) 数据集road net-TX图3 两种数据集下五种压缩格式的性能指标 可以看出,MPKI高,IPC低时会增加其执行时间,同时CSR压缩格式表现出了更少的执行时间、数据移动量以及计算量,DCSC压缩格式的计算量和功耗相对较小;CSCI压缩格式的执行时间和数据移动量相对较长,COO压缩格式的计算量较大而CSC压缩格式的各项指标均居中。这是因为CSR压缩格式记录了各个顶点作为活动顶点时的行偏移量,减少了顶点遍历的时间和计算量。当CSCI和COO两种压缩格式作为输入时,每个活动顶点的访问都需要遍历所有顶点从而找到与当前活动顶点相连的目标顶点。CSC和DCSC压缩格式记录的是图数据中边的源点,无法直接对其进行单源最短路径算法处理,需要在实现过程中对数据进行预处理操作,所以其性能相比CSR压缩格式较差。综上所述,当执行时间作为主要参考指标时应优先选择CSR压缩格式;在计算操作量受限制的情况下,则选择CSR压缩格式作为数据集的输入格式;在硬件环境受限时并且需要尽可能减少功耗时,也可选择CSR压缩格式,它具有更少的数据移动,可提升图计算加速器的性能;在考虑内存占用情况时,选择使用DCSC压缩格式;而在需要提高缓存命中率的情况下,应选择CSC压缩格式。 (1) 执行时间。两种数据集在不同压缩格式下每条边的执行时间如表3所示。可以看出CSCI格式边的执行最长而CSR压缩格式边的执行时间最短,几乎为CSCI格式的一半,当数据量足够大时甚至相差更多,CSC与DCSC格式执行时间接近,COO格式的执行时间居中。因此对于遍历类应用而言,在考虑边的执行时间时,优先选择CSR压缩格式作为数据集的输入格式。 表3 两种数据集五种压缩格式下的执行时间 单位:ms (2) 数据移动量。表4列出了两种数据集在不同压缩格式下每条边的数据移动量。可以看出,对于顶点与边相对较小的Wiki_Vote数据集而言,每条边的需要成千上万的数据移动量,而对于road net-TX数据集,每条边所需的数据移动量甚至可达上千万。对比五种压缩格式,可以发现CSR压缩格式的数据移动量远小于其他四种格式,CSC和DCSC的数据移动量接近且居中,COO和CSCI的数据移动量相对较大。因此对于遍历类应用而言,在考虑边的数据移动量时,应选择CSR压缩格式作为数据集的输入格式。 表4 两种数据集五种压缩格式下每条边的 数据移动量(指令数/边数) (3) 功耗。两种数据集在五种压缩格式下每条边的功耗如表5所示。可以看出CSR压缩格式的消耗的能量最少,这是因为CSR压缩格式记录了当前活动顶点的行偏移量,无须遍历所有顶点便可以准确定位到目标顶点,这大大地减少了功耗,所以其他四种格式消耗的能量相对较多。因此对于遍历类应用而言,选择CSR压缩格式能够有效地减少功耗。 表5 两种数据集五种压缩格式下每条边的功耗 单位:J (4) MPKI。两种数据集在五种压缩格式的L1、L2和L3级cache MPKI分别如表6、表7和表8所示。可以看出,在所有压缩格式下,L1级cache MPKI都小于3,L2级cache MPKI几乎小于L1级cache MPKI的一半甚至更多,L3级cache MPKI更小,因此我们只关注各个压缩格式的L1级cache MPKI。对比结果可以发现CSC压缩格式具有更小的L1级cache MPKI,因此选择CSC压缩格式可以有效提高遍历类应用的缓存命中率。 表6 两种数据集五种压缩格式下L1级cache MPKI (misses/kilo_instructions) 表7 两种数据集五种压缩格式下L2级cache MPKI (misses/kilo_instructions) 表8 两种数据集五种压缩格式下L3级cache MPKI (misses/kilo_instructions) (5) 计算量。表9列出了两种数据集在不同压缩格式下每条边计算量。可以看出CSR压缩格式具有更少的计算量,而COO与CSCI压缩格式的计算操作相对较多,高达CSR压缩格式的数倍。因此在计算量受限制的情况下,遍历类应用应优先选择CSR压缩格式作为数据集的输入结构。 表9 两种数据集五种压缩格式下每条边的计算量 (指令数/边数) 分析结果可以看出五种压缩格式在不同的需求下有着各自的特点。COO压缩格式在存储图数据时简洁明了,但对于顶点的邻接边和顶点的查询及访问效率较低。CSC和CSR压缩格式占用内存较小,存储效率高,其中CSC可以高效地查询顶点的入边信息,CSR可以高效查询顶点的出边信息。DCSC压缩格式对CSC中源顶点再次进行压缩,对于稀疏图数据来说存储效率最高。CSCI压缩格式可以根据列标识相关数据,计算活跃顶点在存储中的物理地址,实现“精确”访问,但内存占用较大。 同时,对于SSSP算法而言,CSR是适合单源最短路径算法的数据结构。因为CSR压缩格式顶点的邻接点信息递增顺序存储,其处理时间最短而且能有效缩短执行时间,减少计算操作量和数据移动量,同时降低功耗。选择DCSC压缩格式能减少图数据的内存占用。选择CSC压缩格式能提高其缓存命中率。 本文通过分析两种数据集的五种压缩格式(COO、CSC、CSR、DCSC以及CSCI)在SSSP算法的性能数据,发现:对于SSSP算法,当硬件环境受限时,应当优先选择CSR压缩格式,能有效减少功耗、计算量和数据移动量;当考虑图应用的缓存命中率时,选择CSC压缩格式作为其图数据输入格式;当内存受限时,选择DCSC压缩格式作为数据输入格式。具体原因如下:CSR压缩格式记录了当前活动顶点的行偏移量,在算法处理时无须遍历所有顶点便可准确定位目标顶点,有效减少了算法的执行时间、计算操作量、数据移动量以及功耗。而考虑其cache MPKI时,选择CSC压缩格式可以有效提高遍历类应用的缓存命中率。考虑内存占用情况时,选择DCSC压缩格式可提高图数据的存储效率。 综上所述,在面对不同的应用环境、不同的性能要求时,根据实际需求以上述结论为依据进行调整可有效提高图计算加速器的性能。1.2 五种压缩格式分析

2 实验环境建立与性能指标定义
2.1 硬件平台
2.2 数据集选取
2.3 分析工具perf[23]
2.4 性能指标定义
3 不同压缩格式的内存占用及特性化
3.1 不同压缩格式内存占用情况

3.2 不同压缩格式的特性化分析



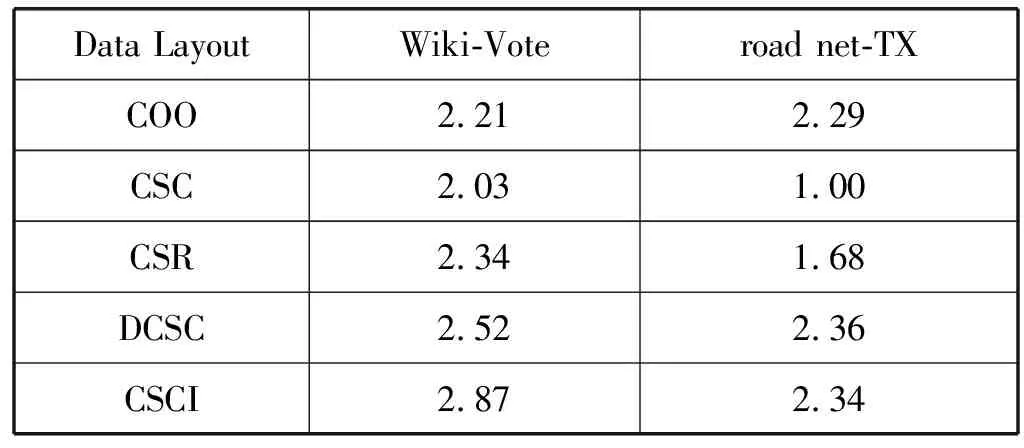
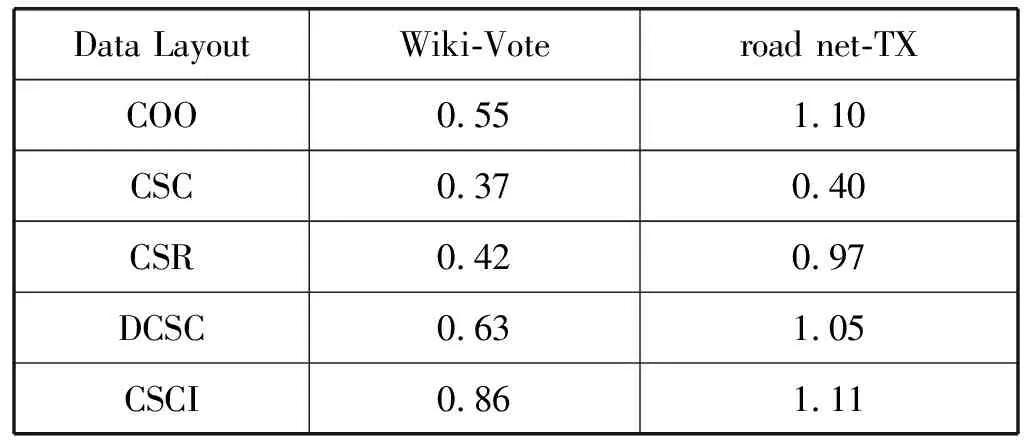

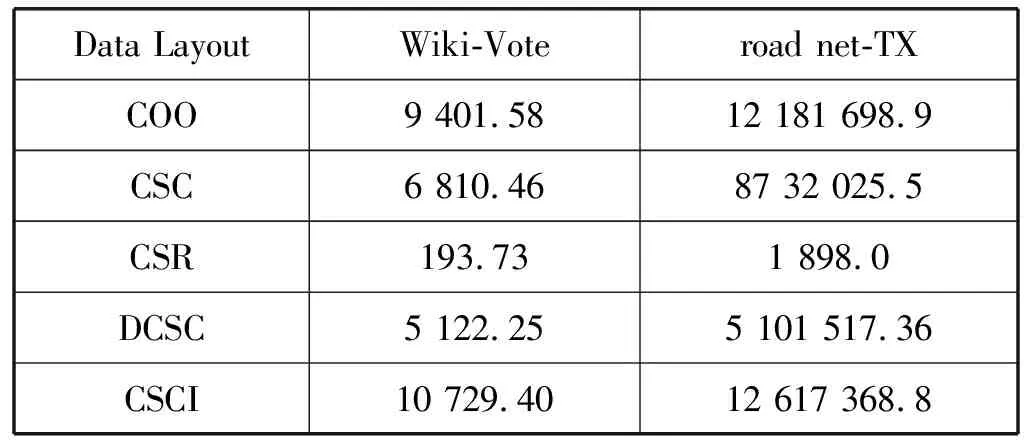
3.3 综合分析
4 结 语
