基于结构分解的分布式RDF图模式匹配优化算法
2022-07-12孙云浩邢维康李冠宇李逢雨
孙云浩 邢维康 李冠宇 韩 冰 李逢雨
(大连海事大学信息科学技术学院 辽宁 大连 116026)
0 引 言
如今,由于知识图谱的兴起,越来越多的数据集采用资源描述框架(Resource Description Framework,RDF)的格式发布和维护数据,它将一个数据集表示为一组
早期的RDF存储,如RDF-3X[4]、SW-Store[5]、HexaStore[6],通常使用集中式设计。随着RDF数据集规模和查询规模增加,保证查询的低延迟性成为了一项挑战。作为回应,很多研究致力于开发可扩展和高性能的系统来索引RDF数据和处理SPARQL查询。如StarMR[7]、TriAD[8]、Trinity.RDF[9]、Wukong[10]和Stylus[11]等通过使用分布式存储,来应对不断增长的数据量。
虽然RDF数据集能够以三元组的形式作为元素存储在关系表中(即三元组存储)[4,8,12-13],但RDF数据集本质上是一个带标签的有向多边图,所以也能够以原生图形(即图形存储)的形式进行存储管理[9,11,14,25]。文献[10-11]也表明,使用三元组存储虽然可以方便地继承很多关系数据库上成熟的查询优化技术,但查询处理过度依赖于大表索引所产生中间结果的连接操作,这通常会产生大量无用的中间数据。此外,使用关系表来存储三元组可能会限制通用性,很难支持RDF数据上的其他图形分析,如可达性分析、最短路径和社区检测等。
本文遵从基于图形的设计,使用基于内存的分布式架构,将RDF数据集存储为原生图形式,并利用图探索策略来处理查询。由于处理图探索问题的复杂性,而将查询图Q的节点分解为核心(Core)、路径(Path)、边际(Marginal)节点三部分,并依据分解结构提出了一种查询图的生成树模型Tq。使得图探索过程转化为沿着Q的生成树Tq迭代地扩展从Q到数据图D的嵌入(embedding),同时检查与Tq中新扩展的节点相邻的非树边。最后,根据各部分结构的特征,通过在分布式并行计算中分割匹配过程及推迟笛卡尔乘积操作,来尽可能缩减查询的中间结果数及增大查询并行度以降低查询延迟。
本文的主要贡献如下:(1) 根据查询图中各部分结构在分布式环境中的匹配特点,提出了查询图的CMP节点分解模型。针对RDF数据图节点为语义实体的特点,提出了基于类型的统计概要图,并利用统计信息对节点分解结构进行加权计算。(2) 在加权的查询图上,提出了以节点为核心的代价模型并结合最小生成树思想将复杂的图探索问题转化为查询执行树,得到了更高效的查询执行序列。(3) 为进一步提高算法性能,提出了两种优化策略:一是通过推迟笛卡尔积操作,大量压缩了核心结构匹配时包含全历史信息的路径数目;二是通过结构分解将匹配过程分割,使得路径结构匹配可以无冗余计算地高速并行执行。(4) 在基准合成数据集LUBM[26]和真实数据集YAGO2[27]上进行了实验,验证了算法的有效性、高效性;针对不同数据集规模及集群节点数目的变化进行了实验分析,验证了算法的可扩展性。
1 预备知识及相关工作
1.1 RDF图及SPARQL查询
定义1RDF数据图。RDF数据图D(V,E,L,φ)是一个有向标签图,其中V表示节点集;E是连接V中节点的有向边集;E:(v,v′)是一个有向函数,表示从v到v′的一条有向边,其中v,v′∈V;L表示边和节点标签集;φ:V∪E→(L∪var)表示一个将节点或边映射到对应标签的标签函数。
图1是从LUBM[26]数据集中摘取的RDF图示例。为了更简洁地表述,对节点URI进行了压缩表示,没有涉及RDF标准定义中的空节点(Blank Node),空节点问题与本文内容是正交的。
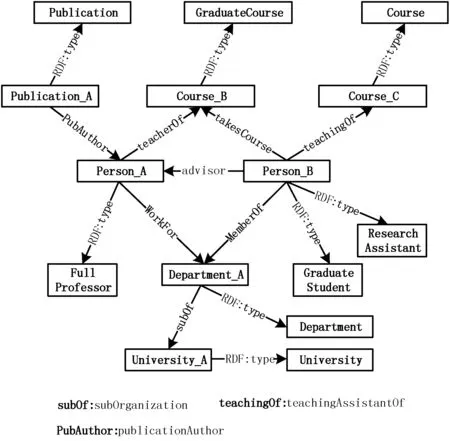
图1 RDF数据图示例
SPARQL是W3C推荐的RDF数据集的标准查询语言。最常见的SPARQL查询类型定义如下:
Q:SELECTRDWHERETP
其中:RD是对结果的描述,TP是一组三元组模式。每个三元组模式的形式为
定义2RDF查询图。RDF查询图Q是SPARQL查询类型的图形化表示。SPARQL中的每一个三元组模式TP
定义3模式匹配。给定一个RDF图D和SPARQL查询Q(∧1≤i≤nTPi),模式匹配Q(D)定义为:
(1) 设f是从Q到D的一个映射;
如图2(a)所示,SPARQL查找选修了由其指导教授所讲授课程的学生及对应的选修课程组合。查询可以图形化来表示,如图2(b)所示。图2(c)中显示了该查询在图1所示的示例RDF图中的模式匹配结果Q(D),即结果描述RD为{?X→Person_B,?Y→Person_A}。

(a) SPARQL原语 (b) 查询图表示Q (c) 结果描述RD图2 示例RDF图上的SPARQL查询示例
1.2 现有的解决方案
本节介绍最先进的RDF系统中所采用的几种代表性方法。
1) 关系方法(scan-join)。大多数RDF系统将RDF数据作为关系数据库中的一组三元组表进行存储和索引。如Abadi等[5]提出的SW-store将RDF三元组垂直分区到多个属性表。RDF-3X[4]和Hexastore[6]通过直接在B+-tree中冗余地存储三元组SPO的多种排列(如PSO、POS)来实现基于索引的查询方案,这可能导致多达15个这样的B+-tree[15]。Peng等[16]给出了一种能够根据查询负载优化图划分和存储的RDF图存储方案,查询处理通常包括扫描(scan)和连接(join)两个阶段。在扫描阶段,查询引擎将SPARQL查询分解为一组三元组模式。例如,对于图2所示查询,三重模式TP包含{?X advisor ?Y}、{?X takesCourse ?Z}、{?Y teachOf ?Z}三个三元组模式。对于每个三元组模式,通过扫描索引或表来生成符合每个模式的中间结果绑定。在连接阶段,将扫描阶段的中间结果绑定依照连接计划(例如左深连接或者平面连接)进行连接,以产生查询的最终答案。
2) 基于MapReduce的方法。分布式系统H-RDF-3X[17]和SHARD[18]在多个计算节点上水平划分RDF数据,并将Hadoop作为跨节点查询的通信层。H-RDF-3X通过最小边割方法METIS[19]将RDF图分割成指定分区数。然后,在每个分区上利用1-hop或者2-hop复制来扩展分区边界以保证小直径查询可以在分区内部获取完整答案。两个系统的查询处理都使用迭代的Reduce-side连接,其中Map阶段进行选择,Reduce阶段执行实际连接[20]。但是对于复杂查询,Map阶段扫描大量的RDF元组和迭代运行MapReduce作业的开销十分昂贵。Lai等[21]提出了基于TwinTwig结构分解的MapReduce分布式高效子图枚举算法,但该算法仅用于无向无标签图。S2RDF将SPARQL查询转换为Spark分布式计算框架上的RDD操作,其离线建立了大量索引,用于加速在线查询,但对于大规模知识图谱,索引构建时间开销可能很高[22]。TriAD[8]中的工作表明,如果分布式查询过程中需要交互,应该避免通过Hadoop进行连接。
3) 原生图方法。最近许多以原生图格式存储RDF数据的方法被提出。这些方法通常使用邻接表作为存储和处理RDF数据的基本结构。此外,这些方法通过使用复杂的索引,如TripleBit[13]、BitMat[14]和gStore[23],或者使用图形探索(graph-exploration),如Trinity.RDF[9]和Wukong[10],在进行最后的连接操作之前剪枝许多无望形成结果的三元组。原生图方法能更有效地支持更多类型的图形查询,例如可达性、社区检测、最短路径及随机游走(部分已经包含在SPARQL1.1标准中),这也是RDF-S样式推断所必须的。Trinity.RDF中只采用一步剪枝的图探索策略虽然避免了指数级路径结果的保存,但最终需要利用一台机器来聚合所有片段结果以对结果进行最终连接。文献[8,10]中的研究发现,最终的连接很容易成为查询的瓶颈,因为所有结果都需要聚合到一台机器中进行连接,Wukong在LUBM[26]上的实验表明,一些查询在最终连接上花费了90%以上的执行时间。Wukong采用全历史剪枝的策略来避免最终连接,但其只是借鉴关系方法中基于谓词连接的代价模型来指导查询执行,没有针对图探索策略及复杂查询结构来进行执行序列优化,也没有压缩基于全历史剪枝策略的中间结果,造成冗余验证及不必要的网络传输。
针对上述问题,本文提出了一种新型的查询分解模型并以此优化查询执行序列,并根据各部分结构的特征,分割匹配过程及推迟笛卡尔乘积操作,来尽可能缩减查询的中间结果数及增大查询并行度来降低查询延迟。
2 基于结构分解的图模式匹配
本节提出一种基于图探索模式的新的RDF并行计算模型,旨在尽早地对匹配过程中的结果路径进行剪枝并延缓笛卡尔乘积过程。
2.1 CPM查询图分解模型
为了更好地支持图探索模式和复杂查询,将查询图Q中的节点进行分解,根据查询图各部分结构的特征,来尽可能缩减查询的中间结果数及增大查询并行度以降低查询延迟。
定义4无向查询图Qud。对于给定的查询图Q,将图中的每一条边都替换为无向边,所构成的无向图定义为无向查询图(记为Qud)。
为了方便后续表述,如图3所示,将无向图Q中的查询节点标示为圆形,并采用类树形的结构划分层次。转换成无向图,是为了泛化原查询图中边关系的指向,Qud中各层次之间的边所对应的原始边既可以由低层次指向高层次,也可以由高层次指向低层次。

图3 查询图Q及其无向查询图Qud
定义5核心节点集VC。给定查询图Qud,对于能完整遍历Qud中所有节点的任意生成树Tq,核心节点集VC={u|u∈Qud,∃(p∈Pre(u),Tq←Qud),p是Tq的非树边},其中Pre(u)表示与节点u关联的谓词边,即对于核心节点中的每一个节点,都存在一条边在某棵生成树中为非树边。
如图4所示,对于由Qud中节点?C、?FP、?S构成的环形结构,对于不同的查询图生成树Tq,谓词边TO、TC、Adv都可能作为非树边出现,与非树边相关联的?C、?FP、?S节点均为核心节点。
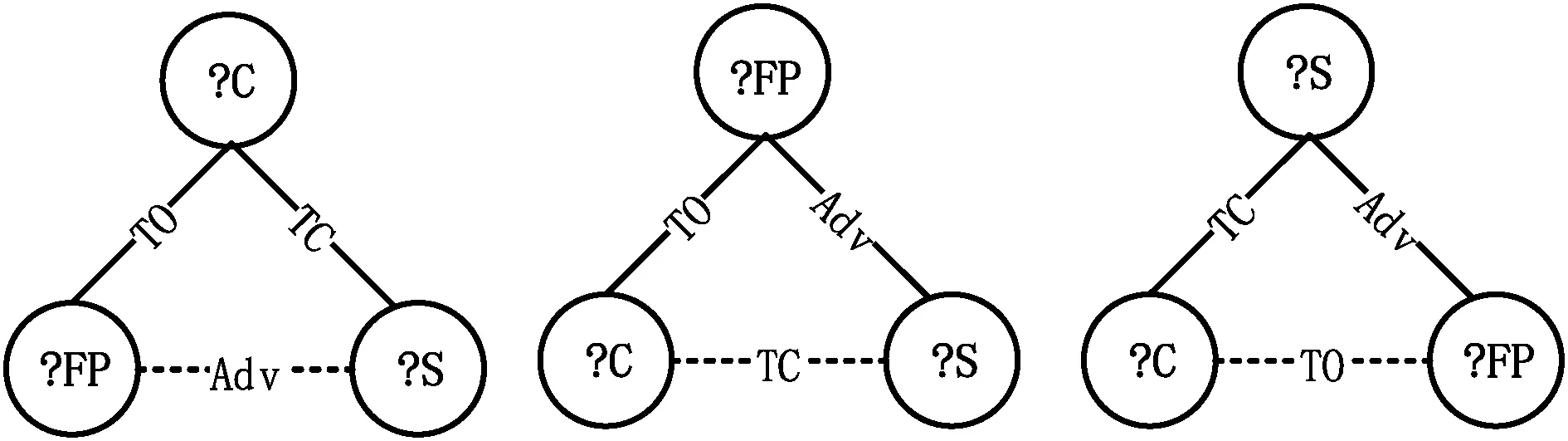
图4 核心节点集结构
一个良好的匹配序列需要尽早进行非树边的验证,一方面这将修剪大量无法形成最终结果的路径绑定(即中间结果),另一方面也减少了非树边缘检查的总数。因此,算法将VC中的节点作为匹配序列的起始部分,这对高效的子图匹配至关重要[24]。
定义6路径节点集VP。给定Qud,路径节点集VP={u|d(u)≥2,∃(至多一个u′∈Qud.Adj(u),u′∈VC)},其中d(u)表示节点的度,Qud.Adj(u)表示节点u的邻接节点集,即路径节点集包括所有的节点度大于等于2且至多只与一个核心节点相连的节点。
如图5所示,对于无向查询图Qud,?R、?D、?P均为路径节点,VP中节点在任何生成树Tq中都不与非树边相连,所以在进行节点验证时并不需要利用到历史信息,可以减少通信代价且可以并行化操作。路径节点的匹配紧跟在核心节点之后并行执行。
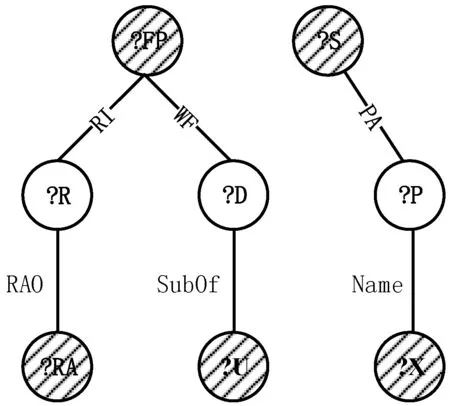
图5 路径节点集结构
定义7边际节点集VM。给定无向查询图Qud,边际节点集VM={u|u∈Qud,d(u)=1},即边际节点集包括Qud中的所有度为1的节点。
如图6所示,对于无向查询图Qud、?RA、?U、?X、?TA均为边际节点。在本文的存储模型中,由于边际节点只存在一条谓词边约束,所以完全可以在其邻接节点上进行节点的匹配验证,而无须将中间结果传递到边际节点。边际节点的候选集也不会对后续的匹配有所帮助,所以作为整个结果的笛卡尔积部分,应将其放在匹配的最后进行处理。

图6 边缘节点集结构
2.2 核心节点匹配序列
根节点是匹配顺序中的第一个节点,所以要从核心节点集VC中选择根节点。本节中,优化器结合对数据图预处理而生成的RDF特有的统计概要,对匹配中间结果进行更加准确的估计,制定更加合理的匹配序列(seq)。
直观来讲,倾向于选择具有较少的局部匹配结果,以及较大的度(只统计核心节点内部的度)的节点作为初始节点。较少的匹配结果意味着更低的网络传输代价;较大的度意味着有更多的机会在匹配早期阶段修剪绑定路径。类似于文献[24],本文选择根节点:
(1)
式中:d(u)是u关联到核心节点内部的度;cost(u)是对核心查询节点u的预估局部匹配结果数。得到cost(u)有不同的策略,不同的策略会有不同的代价。本文使用预处理阶段生成的RDF特有的统计概要来对进行估计。接下来将讨论统计概要的获取过程。
W3C提供了一组词汇表(作为RDF标准的一部分)来编码RDF图丰富的语义信息,例如类型谓词(rdfs:type)提供了将RDF图的节点分组成不同类别的功能。与一般标签图不同,RDF图节点标识的是实体/文本信息,实体的语义特性导致了相同类型的节点通常具有类似的谓词组合,便于统计。

对于每一个type类型,C(type)表示对应数据类型的节点在数据图中的基数。


图7 RDF摘要统计示例
对于RDF图G上的查询Q,用Pre(u)表示查询节点u具有的属性(也就是谓词)集合,Pre(u)={pi|∃
P(u)={pi|∃(u′∈VC且(u,pi,u′)∈Qud)}P′(u)={pi|∃(u′∉VC且(u,pi,u′)∈Qud)}
进一步地,根据查询图Q中谓词p与u的出入边关系,划分P(u)=P-in(u)∪P-out(u),形式化为:
P-out(u)={pi|∃(u′∈VC且(u,pi,u′)∈Q)}P-in(u)={pi|∃(u′∈VC且(u′,pi,u)∈Q)}
同样可得,P′(u)=P′-in(u)∪P′-out(u)。
基于上述讨论,得出了起始节点的局部匹配数cost(u)的估算公式:
cost(u)=C(u.type)×des(u)×cut(u)
(2)
(3)
(4)
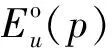
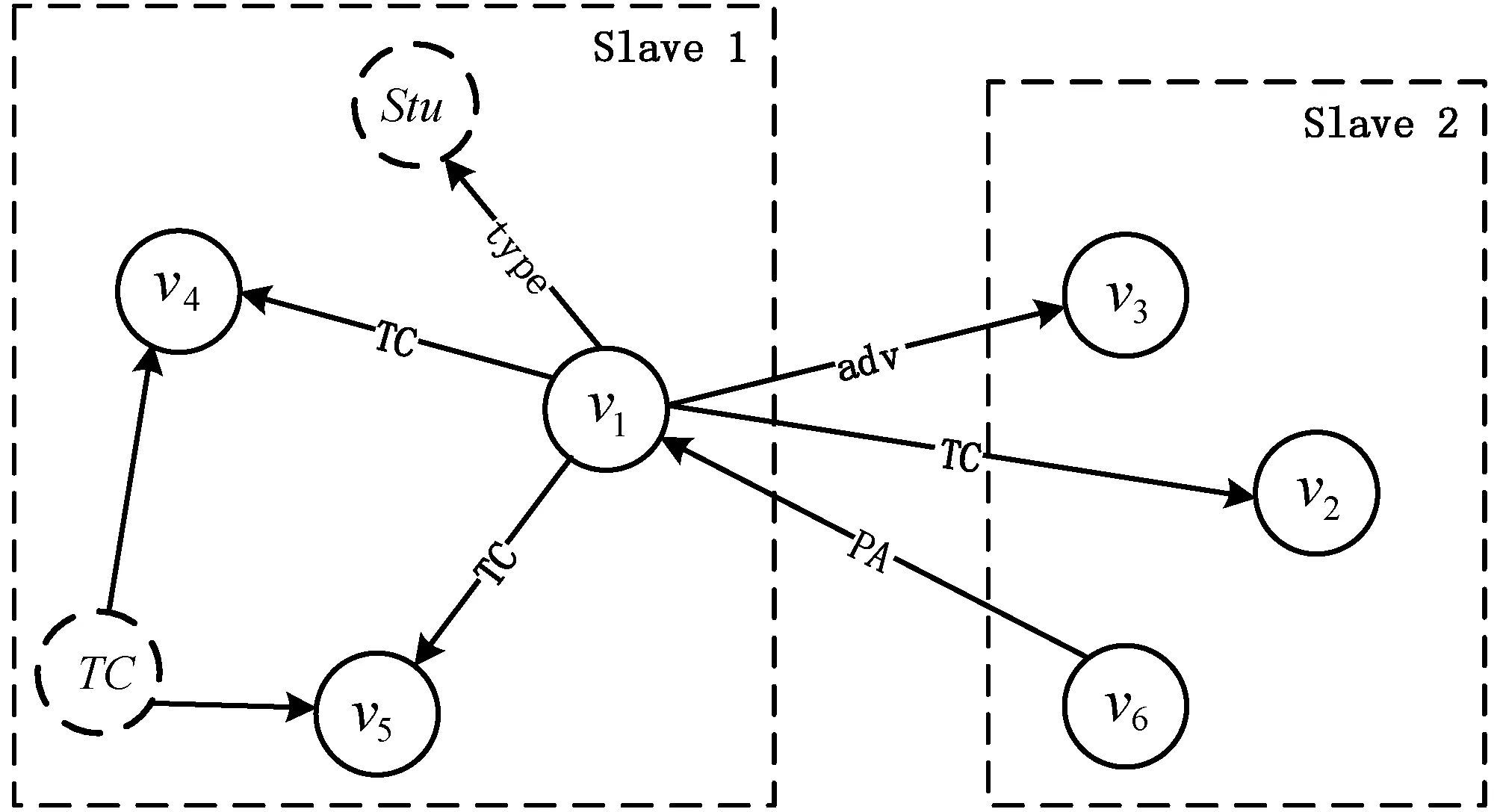
通过式(1)-式(2),具有最小代价的节点被选为根节点。例如图7中示例,核心节点集VC={u1,u2,u3}中三个节点所对应d(u)均为2。通过计算,cost(u1)为1 952,cost(u2)为3 489,cost(u3)为39 124。因此,选取u1节点为核心节点中查询搜索的起始节点。
定义8核心结构权重图Gw(VC)。给定核心节点集VC,核心结构图Gw(VC)中的权重w计算为:
(1) 对于模式Tp=

式中:Tpcut(u)为核心结构中所有内部模式(边)的选择度的乘积,权重值w表示核心节点在指定边的预估计中间结果数。
对于图7所示查询图及概要统计图,计算得到的核心结构权重图如图8所示。给定起始节点r,在Gw(VC)上结合最小生成树思想得出最低代价的核心节点匹配序列,并依次记录节点的树边与非树边。

图8 查询图的核心结构权重图示例
如算法1所示,算法1-4行将每个节点的最低连接代价key值设置为∞,然后初始化匹配序列,并将根节点r的key值设置为0,以便在循环中第一个执行;算法5-17行借鉴Prim算法思想寻找以r为起始点的,核心结构权重图Gw(VC)上的最小代价生成树(即匹配序列)。当以一个二叉最小堆来记录u.key时,1-4行的时间成本为O(|VC|);While循环一共要执行|VC|次,其中Extract_Min(Q)操作选择出队列Q中具有最小key值的节点u并将其移出队列,单次操作的时间成本为O(lg|VC|),所以函数总的时间代价为O(|VC|lg|VC|);算法8-16行的for循环执行的总次数为O(E),通过对节点设置标志位可以在O(1)内实现对v∈QorVnt的判断,算法11行中赋值操作对应的堆操作时间成本为O(lg|VC|)。所以,用E表示Gw(VC)中边的数量,总的时间代价为O(|VC|lg|VC|+Elg|VC|)=O(Elg|VC|)。
算法1核心节点匹配序列(MatchingOrder)
输入:核心节点集VC,匹配根节点r,核心结构权重图Gw(VC)。
输出:核心节点的匹配顺序seq。
1.for each查询节点u∈VCdo
2.u.key←∞;
3.seq←∅;r.key←0;
4.Q←VC;Vnt←∅;
5.whileQ≠∅ do
6.u←Extract_Min(Q);
7.seq←seq∪u;
8.for eachv∈Gw(VC).Adj(u) do
9.ifv∈Q
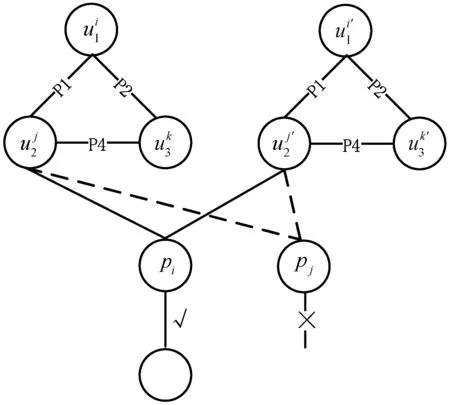
10.ifw(u,v) 11.v.key←w(u,v); 12.ifv∈Vnt 13.u.nt←u.nt∪e(u,v); 14.else 15.u.t←u.t∪e(u,v); 16.Vnt←Vnt∪v; 17.MatchingEdgeOrder(u,u.nt,u.t); 18.returnseq 查询序列确定后,可以将无向查询图重构为一棵查询树(记为Tq)。基于图探索的RDF存储结构保证了对同一节点的邻接关系都存储在与之相同的机器上。节点验证及查询路由(Query Routing)与查询图的BFS过程类似,完整的查询图只需要在Tq中补全缺失的非树边。 如图9所示,若查询图中核心节点部分所构成的图形如图9(a)所示,经过计算选取u1为起始节点,且查询执行序列为seq= (a) (b)图9 核心节点图G(VC)及查询计划树Tq 节点边缘匹配顺序算法流程如算法2所示。 算法2节点边缘匹配顺序(MatchingEdgeOrder) 输入:查询节点u,节点的非树边集u.nt,节点的树边集u.t。 输出:u上的边缘匹配序列u.order。 1.u.order←∅; 2.for eachv∈VP.Adj(u) orv∈VM.Adj(u) do 3.u.t←u.t∪e(u,v); 4.Whileu.nt≠∅ do 6.u.order←u.order∪p; 7.u.nt←u.nt-{p}; 8.Whileu.t≠∅ do 10.u.order←u.order∪p; 11.u.t←u.t-{p}; 14.returnu.order 图10 全历史剪枝下各中间路径验证匹配过程 对于u2的候选节点,u2.nt表示Tq中与u2相连的未匹配非树边集合,即边p4;u2.t表示与u2相连的未匹配树边集合,即边p3。当查询路径执行到u2节点时,由于u2.nt不为空,固先匹配非树边p4,再匹配树边p3。图10中实线箭头所示过程为非树边验证,虚线箭头所示部分为树边匹配过程。按照核心节点执行序列依次执行各节点,直到所有节点都完成路径匹配。 图11显示了数据图上依据v-id进行hash分区的一个示例,其中虚线节点代表谓词或类型所对应的虚拟节点。类似于文献[10-11],键值存储创建了一个RDF的图模型,每个RDF实体被表示为具有唯一id的图节点,节点id与谓词id及出入度关系组成的三元组结构实现了细粒度的key值表示,Value表示对应索引的候选集合,如图12所示。这十分便于获取各查询节点的候选集合。 图11 数据图分区示例 图12 字典编码与索引结构 算法将查询计划传递到每一个计算节点。对于变量节点,根据不同情况,计算节点利用类型或者谓词对应的倒排索引(Idx-t,Idx-p)查询到本地全部的初始根节点r的候选,在所有计算节点上开始匹配任务。 在先前的图探索方法Trinity.RDF和Wukong中,查询序列的生成借鉴了关系方法中的成熟模型,其类似于关系方法中join阶段的连接计划确定(例如左深连接计划树),以谓词关系的连接顺序主导来确定节点匹配序列。但是,RDF本质上是一个带标签的有向多边图,关系模型无法充分利用查询图的结构特征(例如环形或者星形结构)来指导查询,无法充分发挥图探索策略的优势(即与关系方法相比,随着探索的进行,在匹配早期修剪大量无望的中间结果)。 例如,在图7(a)所示结构中,若关系主导的匹配序列为seq= 另一方面,图探索策略中关系主导的匹配序列在分布式环境下可能导致中间结果在计算节点间的往复传递。与关系方法中的join连接不同,join连接是将scan阶段所有收集到的中间结果汇总到同一节点进行连接工作,join阶段类似于单机环境。图探索策略由于数据的分布存储,不同实体节点可能被划分到不同的计算节点,如图11所示。同一实体节点在查询图中具有的谓词关系可能还未完全验证,匹配序列即要求将匹配的中间结果传递到其他节点,进行后续谓词关系的验证,而后又再次返回原节点,进行剩余谓词关系的探索。 例如,在图7(a)所示结构中,关系主导的匹配序列仍为seq= 由于关系主导的匹配序列的一系列问题,本文提出了一种结构主导的分布式子图匹配算法SDSM,基于各部分结构在分布式环境中的匹配特点,利用CPM分解模型进行查询图的结构分解,以结构信息指导匹配序列,尽可能地缩减查询的中间结果数,提高查询效率。 在2.2节与2.3节中,为了降低中间结果数量,制定了以结构为主导的严格的匹配序列,并完成了核心部分节点结果的匹配(记为MC)。各中间结果路径在核心节点部分都得到了唯一(各不相同)的路径绑定,而匹配过程中与核心节点相连的路径节点或者边际节点则以候选集的形式保存,如图13所示。 图13 中间结果绑定 路径节点由于不存在非树边,所以无须用到历史信息剪枝,没有必要携带完整的历史信息来造成网络传输的负担。对于核心节点遍历获得的中间结果,如果采用文献[10]中的全部中间结果独立计算策略,且携带完整的历史信息直到整个查询结束,不仅会增大网络负担,同时也造成了节点的重复计算。 图14 不同中间结果映射到相同的路径节点 SDSM算法通过分割核心节点匹配与路径节点匹配两个过程来实现高并发的子路径匹配连接,如算法3所示。各路径分支以MC中产生的路径节点候选作为起始,执行一个个独立的子路径查询,路径匹配过程可以无冗余地并行化执行,提高了查询的并发度。各路径匹配结果MP最终在主机节点上执行轻量级的连接形成最终匹配结果M。 算法3结构主导的分布式子图匹配算法SDSM 输入:查询图Q,索引Idx。 输出:SPARQL查询匹配结果M。 master 1.无向查询图Qud←Q; 2.(VC,VP,VM)←顶点分解算法Decomposed(Qud); 3.计算初始节点r; 4.计算核心结构权重图Gw(VC); 5.sed←MatchingOrder(VC,r,Gw(VC)); 6.sendseqto all Slave; 7.匹配结果集M←∅; 8.receiveMc、Mpfrom slave; 9.for each核心节点绑定Mcdo 10.for each路径节点绑定Mpdo 11.M←M∪{MC×MP}; 12.展开M中边际节点VM的笛卡尔积部分; 13.returnM; Slave 14.receiveseqfrom master; 15.Mc←MatchCoreEdge(seq,Idx); 16.sendMcto master; 17.for each路径节点候选ui.c∈Mc.set(VP) do 18.If 19.continue; 20.else 21.MP←MatchPathEdge(ui.c,Idx) 22.sendMPto master. 首先,算法将查询图转化为无向查询图Qud,并依据结构对节点进行分解。在Decompose(Qud)操作中,首先将度数为1的节点全部加入VM并从Qud中删除;然后迭代地将新生成的度数为1的节点加入VP集合并去除,直到没有新的度数为1的节点生成;VC即为剩余节点。算法3-6行依据2.2节的相关讨论及算法1进行计算,随后将查询计划seq发送给所有计算节点。算法14-22行中,依据2.3节及本节相关讨论,在各计算节点依照查询结构执行不同匹配策略,最终得到核心匹配结果Mc、路径匹配结果MP并返回给主机节点。算法8-13行中,主机节点对匹配的中间结果执行轻量级的join连接,并展开相应笛卡尔乘积结果,返回最终答案集M。 本文所有实验均在包括6个相同计算节点的分布式集群上进行,每个计算节点采用Intel(R) Core(TM) i7-7700@3.60 GHz八核处理器,物理内存为16 GB,硬盘大小为1 TB。节点间通信使用1 000 Mbit/s以太网。 实验分别使用了合成数据集LUBM(Lehigh University BenchMark)[26]的4个生成规模和真实数据集YAGO2(Yet Another Great Ontology 2)[27]。相关信息如表1所示,其中#T、#S、#O、#P分别表示三元组数、主语节点数、宾语节点数以及不同谓词数目。 合成数据集LUBM是由利哈伊大学开发的,关于大学本体的一种标准且系统的语义Web存储库评价基准。该基准旨在评估单个现实本体在大型数据集上的扩展查询。本文使用数据生成器UBA1.7生成了4个不同规模的数据集,以便进行可扩展性测试。 YAGO2是一个链接数据知识库,主要集成了Wikipedia、WordNet和GeoNames三个来源的数据,包含1.2亿条三元组,拥有超过1 000万个实体(如个人、组织、城市等)的知识。 表1 数据集详细信息 将SDSM算法的查询性能与TriAD、Wukong,StarMR做对比,相关测试代码及设置来源于文献[7-8,10]。首先,比较了LUBM-2560数据集在6个计算节点(包括一个主节点)上的查询性能。对于查询,本文使用了Atre等发表的基准查询[15],它被许多分布式RDF系统所使用[9-11,14,25]。 如图15所示,在6个查询中,SDSM算法比最快的Wukong分别提高了1.4~3.6倍。将实验分成2组,其中第一组L1、L2、L3(分别对应文献[14]中的Q1、Q3、Q7查询),特别地,因为L2的最终结果为空,源于基准查询中某谓词关系虽然在数据图中大量存在,但在其所对应的实体上基数为0。SDSM中基于类型的摘要统计在制定查询计划时很容易发现了这一点,而Wukong及TriAD却需要遍历大量中间结果;L1跟L3分别构成了较少及较多的最终结果(约为初始候选三元组的1/65 000及1/1 000),图探索的方式比基于关系的模式拥有近1个数量级的速度提升,基于MapReduce的StarMR算法由于其平台计算的局限性,在每个查询上都落后于其他算法1~2个数量级,SDSM依据摘要统计在核心结构上得到了比Wukong更合理的查询节点匹配,并依据非树边的优先匹配更快地剪枝了中间结果,所以得到了更大的性能提升。 图15 LUBM-2560上不同算法的平均查询响应时间 对于第二组更复杂(拥有较多模式)的查询L4、L5、L6(分别对文献[14]中的Q2、Q1、Q7进行了扩展),L4中的查询模式具有很低的选择性,并且由于不存在环结构,极大地降低了借助结构分解及全历史剪枝策略带来的剪枝效果,导致图探索策略与关系方法TriAD相比性能提升较少,SDSM较Wukong的性能提升来源于推迟笛卡尔乘积部分连接的操作带来的收益。查询L5、L6中的环结构分别具有较少及较多核心结构匹配结果,但即使是对于具有较多核心结构匹配结果的查询,核心结构的剪枝力度仍然是最大的,之后在路径节点上无重复的高速并行验证进一步加速了查询。 对于YAGO2数据集上的查询,本文从文献[11-12]收集所需的查询集,查询涵盖了轻量查询和复杂查询。对于YAGO2上的复杂查询Y4、Y5、Y6,实验得到了与LUBM类似的效果,如图16(b)所示,SDSM算法较其他算法分别提升了1.2~2.5倍。不同的是,对于图16(a)中的轻量级查询Y1、Y2、Y3,查询只从常量节点开始进行有限的探索,总查询时间较短(通常在数毫秒之内)。SDSM与Wukong相比在查询计划上的开销稍高一些,但这依然在可接受的范围之内,因为查询的瓶颈通常由那些复杂查询引起,针对复杂查询SDSM算法的效率更高。 (a) (b)图16 YAGO2上不同算法的平均查询响应时间 本文从机器数和数据集大小两个方面对算法的可扩展性进行了评估。 对于第一组实验,如图17所示,当服务器数量从2台逐渐增加到6台时,查询L1-L6的查询时间均随着机器数量的增多逐渐减少,证明了SDSM算法能够有效利用分布式系统的并行性查询。L2由于在查询计划阶段就通过摘要统计得出结果为空,所以查询时间恒定。对于复杂查询L4、L5、L6,查询时间的递减幅度略低于L1、L3,因为更多的分区增加了通过网络传输的中间数据量,但是存储模型仍然有效地限制了这一开销。 (a) (b)图17 SDSM在不同集群节点数目上的表现 对于第二组实验,本文固定服务器的数量为6台,并且生成了不同规模的LUBM数据集来测试算法扩展数据的能力。如图18所示,随着三元组数目从5.3×106增加到346×106,即使是复杂查询,SDSM的查询时间仍能保持近乎线性的增长。因为算法通过对查询图的结构分解,预先携带全历史信息完成了能大幅度剪枝的环形结构的匹配,并推迟了笛卡尔积部分的计算;之后通过无冗余的并行路径节点的查询,最终只需要在主机上进行轻量级的join连接,路径数目不会过于膨胀,具有良好的伸缩性。 图18 SDSM算法在不同数据集规模上的表现 本文提出了一种基于图探索策略的结构主导的分布式子图匹配优化算法SDSM,有效回答了大规模RDF图上的分布式SPARQL查询。SDSM算法依据结构特征将查询图进行分解,结合基于类型的摘要统计和以节点为核心的代价模型,将复杂的图探索问题转化为了查询树模型。此外,通过分割匹配过程及推迟笛卡尔积操作来进行优化,进一步加速了查询。在基准合成数据集LUBM和真实数据集YAGO2进行了实验,验证了算法的有效性、高效性和可拓展性。 图数据划分问题也是一个经典的NP-Complete问题,未来将结合更多的图结构和知识语义信息作为划分标准来进行更细致的图划分算法研究,以便于更好地支持知识图谱上查询的快速执行。2.3 将查询图转化为查询计划树
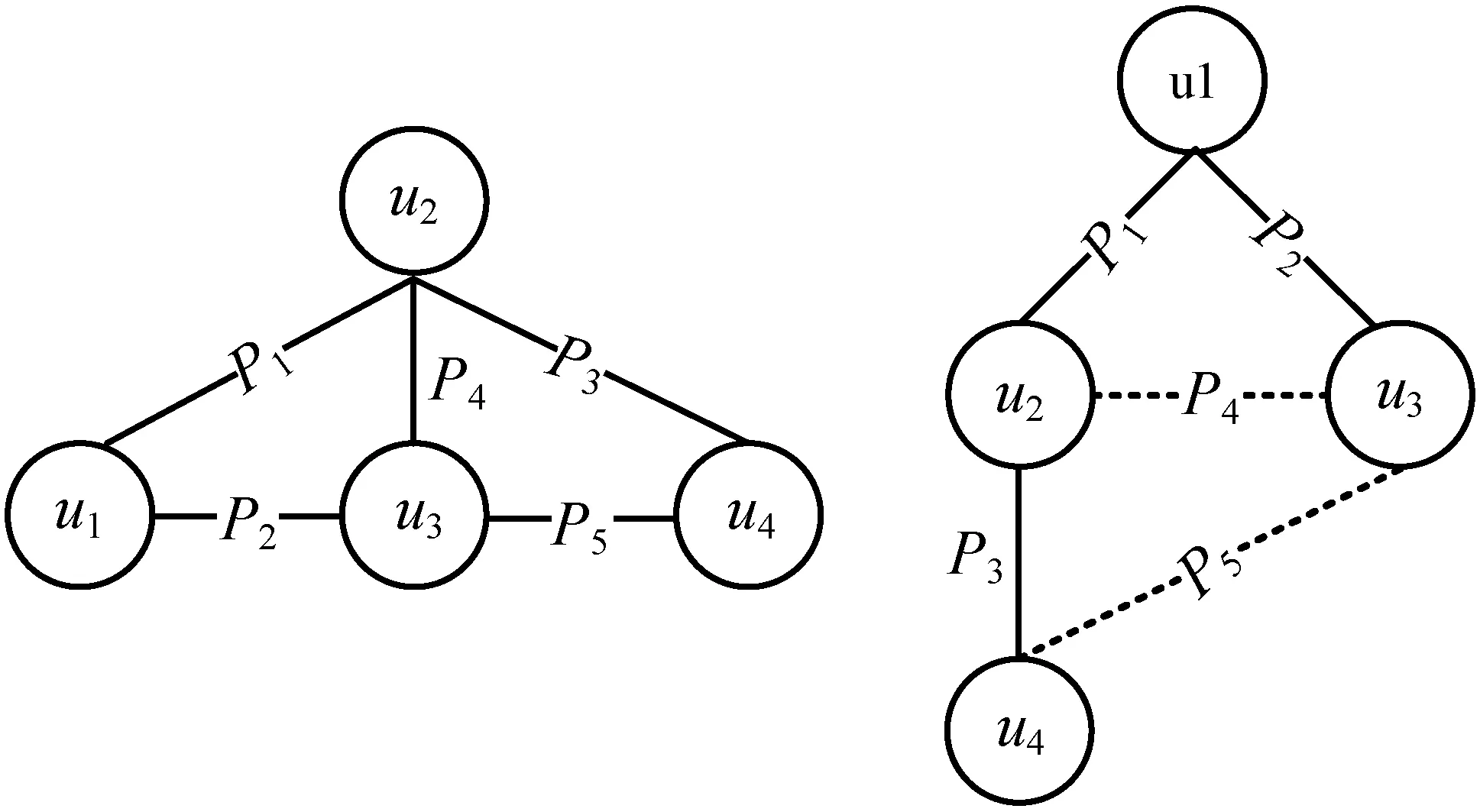
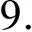



2.4 高并发的子路径匹配连接算法

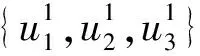
3 实 验
3.1 实验环境与数据集

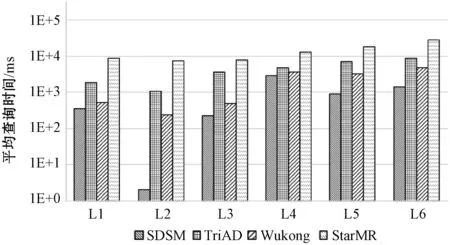
3.2 实验结果

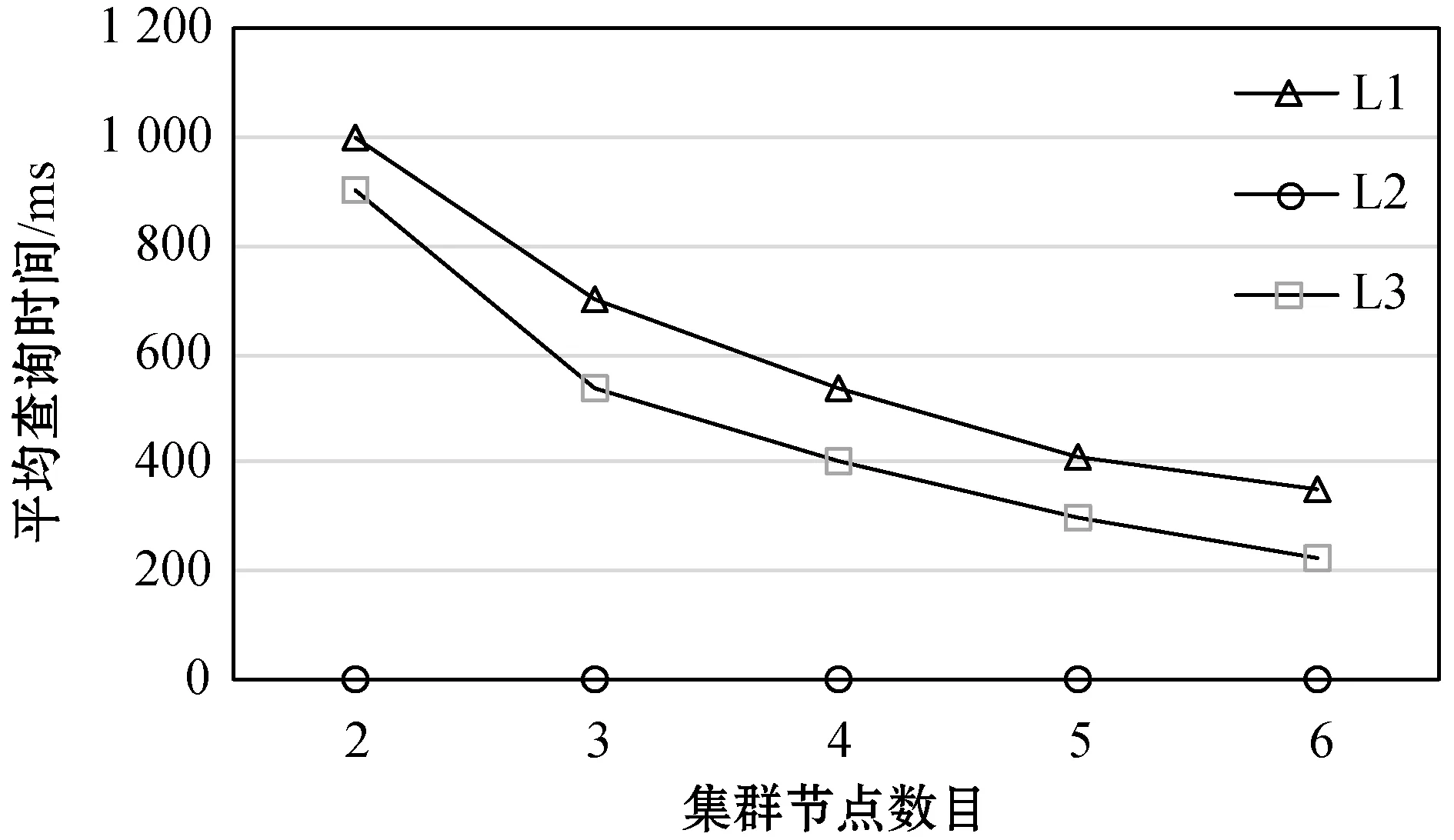
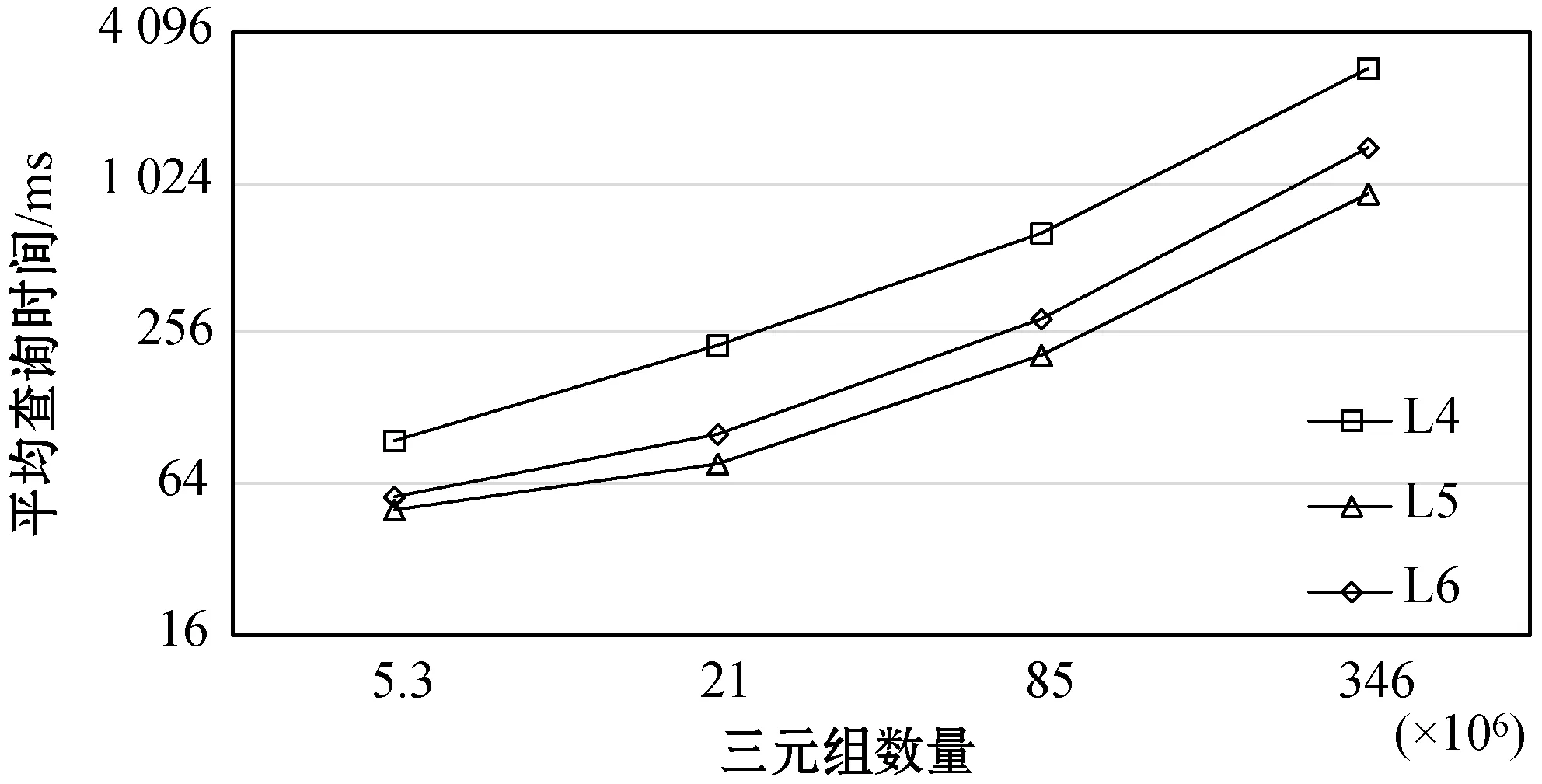
3.3 可扩展性测试

4 结 语
