基于BP神经网络集成学习模型的EMTS坐标校正研究

黄 晨 童维勤* 陈欣如 高明柯 邹一波

1(上海大学计算机工程与科学学院 上海 200444) 2(国网上海市南供电公司 上海 201199) 3(中国电子科技集团公司第三十二研究所 上海 201808) 4(上海海洋大学信息学院 上海 201306)

0 引 言

电磁跟踪系统(Electromagnetic Tracking System,EMTS)能实时获取6自由度的跟踪信息。因其不受视线遮挡影响，十分适用于医学领域[1]，例如术中导航[2-3]和医学图像配准[4-5]等应用场景，也是在增强现实(Augmented Reality，AR)系统中实现跟踪注册的有效途径[6-7]。但EMTS易受工作场景中的金属物体干扰，且当接收器与发射器之间距离增大时，由于磁场衰减将导致精确性显著降低。因此，必须使用相关校正算法对测量值进行校正，避免误差对系统造成干扰。

目前，针对如何提高EMTS精确性的研究工作主要分为两类：第一类方法从EMTS工作原理出发，对由金属干扰造成的磁场畸变[8]和传感器三轴非理想正交[9]等情况进行校正。此类方法需要获得设备工作时的底层参数，不适用于的商业产品。第二类方法在应用场景中进行样本采集，设计数学模型，使用各种拟合或插值算法进行校正，例如空间网格插值[10-11]、线性回归模型[12]、薄板样条插值[13]、BP神经网络模型[14]等。但这些方法在传感器与发射源之间距离较大时都产生了显著的性能下降。

另一方面，已有研究工作都针对在单一工作场景中对EMTS进行校正。当系统部署到新的工作场景中，原校正算法是否还能有效工作，是否需要对系统进行重新采样，还缺乏有效的评估方法。

针对上述问题，本文在设计实现面向医疗培训的AR系统过程中，在回顾总结现有EMTS校正方法的基础上，首先提出一种适用于EMTS的快速采样方法。然后根据测量误差分布规律，提出一种BP神经网络集成学习模型，对三维空间坐标进行校正。最后提出一种在新场景中对坐标校正效果进行评估的解决方案。实验结果表明本文方法能实现高精度的坐标校正，并能在一定程度上提高系统的抗干扰能力。

1 相关工作

为建立数学模型对EMTS的空间坐标值进行校正，首先需要进行坐标值采样。目前使用较多的采样方法是在整个系统工作空间内进行均匀离散采样[10-14]，坐标校正的方法可分为局部插值与全局拟合两大类。

1.1 均匀离散采样

为实现在系统工作空间内进行均匀离散采样，定制了专用的可升降木架操作台。借助该定制木架，将EMTS的接收器依次固定在工作空间内均匀分布的待测点上，记录下测量坐标值与对应的真实坐标值。使用该采样方法所采集样本的可视化效果如图1所示。可见伴随接收传感器与发射源之间距离的增大，测量值的读数已发生明显畸变，必须对其进行校正。

图1 测量值三维坐标散点图

均匀离散采样方法的优势在于，所采集的数据样本能较为全面地反映出EMTS在当前工作空间内测量值的分布情况。理想情况下，当空间网格划分越小，则采样点数量越多，校正的精度也越高。但采样点的数量越多，则工作量越大，可操作性越低。例如，本文AR系统为保证精度，需在X∈[-70,70]，Y∈[5,60]，Z∈[0,70]的空间范围内，以5 cm为间隔进行采样，共计5 220个采样点，需2名操作人员，耗费十多个小时才能完成采样工作。

1.2 基于局部插值的校正方法

磁场强度随着距离的增加以几何级数衰减，当电磁发射器和接收器之间的距离逐渐增大时，测量坐标与真实世界坐标将存在明显误差。若将工作空间划分为多个单元子空间，并认为同一个单元子空间中的任意两点处的磁场强度相等。则当单元空间足够小时，误差将趋于零。基于该思想的局部插值校正方法以空间网格插值法[10-11]为代表。但在实际操作过程中很难获得足够小的单元空间网格，并且伴随单元空间网格数量的增加，用于定位被测点的搜索算法的稳定性和准确性将会下降。

1.3 基于全局拟合的校正方法

文献[12]建立了线性回归模型对EMTS进行校正，但当传感器与发射器距离较远时，测量值畸变较大，已不适用线性回归模型。文献[13]提出一种基于薄板样条函数的EMTS位姿校正方法，通过同时测量磁场空间16个待测点受干扰前后的位姿，对EMTS整个工作空间内测量点的位姿误差进行校正。但该方法适用的工作空间较小，不适用于AR系统在较大范围内对头部视点和手部运动的跟踪。

近年来伴随人工智能技术的快速发展，神经网络算法得到了广泛的应用[15-16]。BP神经网络算法不仅在分类问题领域中得到了发展，在数值分析与回归预测问题方面[17-18]也得到了成功应用。文献[14]首先采用K-means对空间数据进行聚类，在局部采用T-S模糊系统进行预处理，再从全局上利用BP神经网络进行训练，最后采用最小二乘支持向量机进行求解。但该方法对采样数据之间的数值关系依赖性较强，若系统的使用场景发生改变，则现有网络模型无法直接使用，需要重新进行采样。

2 定长连续采样方法

均匀离散采样方法需要借助定制木架提供的外部几何约束来建立待测点测量值与真实值之间的映射。但木架操作不便，采样过程较为繁琐。因此，本文提出一种基于简单外部约束的定长连续采样方法。该采样方法使用一根无弹性塑料绳连接发射源与接收器，使得发射源与接收器之间的距离为固定长度，如图2所示。在采样过程中，保持发射源与接收器之间的塑料绳为绷紧状态，将接收器在工作空间内任意移动。通过调节塑料绳的长度，可以得到若干组数据样本。

图2 定长采样方法

当长度为60 cm时，数据样本分布的可视化效果如图3所示，其物理意义为接收器在系统工作空间内的运动轨迹。理想情况下，该运动轨迹应位于以发射器为圆点，以当前距离为半径的球面之上。

定长连续采样的优势主要有以下3个方面：

(1) 操作便捷。由于定长连续采样方法仅借助连接发射器与接收器的塑料绳所提供的距离作为外部约束条件，且调节距离十分方便，因此采样过程较为便捷。以本文系统为例，对距离d∈[30,100]，间隔为10 cm，每个距离下采集不低于2 000个样本点。整个采样过程，只需1名操作人员，仅耗费数十分钟。

(2) 样本信息丰富。由于EMTS的工作频率较高，1秒内可采集超过100个样本，因此定长连续采样方法在移动传感器的过程中可以很方便获得较为丰富的数据样本。同时，可以将传感器的运动轨迹集中于感兴趣的重点区域以获得足够的数据分布信息，为后续的分析处理提供保障。

(3) 快速评估工作环境。定长连续采样方法可获得待测点的校正坐标值，通过计算校正距离与真实距离之间的误差，能快速评估当前校正方法的有效性。

3 BP神经网络集成学习模型

3.1 建立数据集

本文使用均匀离散采样与定长连续采样两种采样方法在系统工作区间内进行样本采集，基本情况如表1所示。

表1 数据集与样本分布

续表1

对使用均匀离散采样得到的数据集A，点P在测量坐标系Cm中取得的测量值为Pm(xm,ym,zm)，在世界坐标系Cw中对应的真实值为Pw(xw,yw,zw)，dw表示Pw到原点的距离，将Pm与Pw之间的距离定义为测量误差de=|PmPw|。以dw作为横坐标，de作为纵坐标，数据集A中样本的测量误差与距离之间的关系如图4(a)所示。可见原始数据的测量误差不仅与距离有关，还存在较大的固有偏差。由于测量坐标系Cm为EMTS的默认坐标系，与本项目系统中定义的世界坐标系Cw之间存在偏移误差Ce(xe,ye,ze)，因此需要对所有测量坐标值进行偏移修正，即Pm=Pw-Ce。偏移误差Ce可以通过人工测量获得。经过坐标值偏移修正后，数据集A中样本的测量误差与距离之间的关系如图4(b)所示。

(a) 原始分布

(b) 坐标系偏移修正后图4 数据集A测量值误差与距离关系

同理，对使用定长连续采样得到的数据集B，dm表示Pm在测量坐标系Cm中到原点的距离，由于每组样本的dw已知，定义每组样本的误差de=dm-dw。以dw作为横坐标，de作为纵坐标，数据集B中样本的测量误差与距离之间的关系如图5(a)所示。对测量坐标值进行坐标系偏移修正后的效果如图5(b)所示。

(a) 原始分布

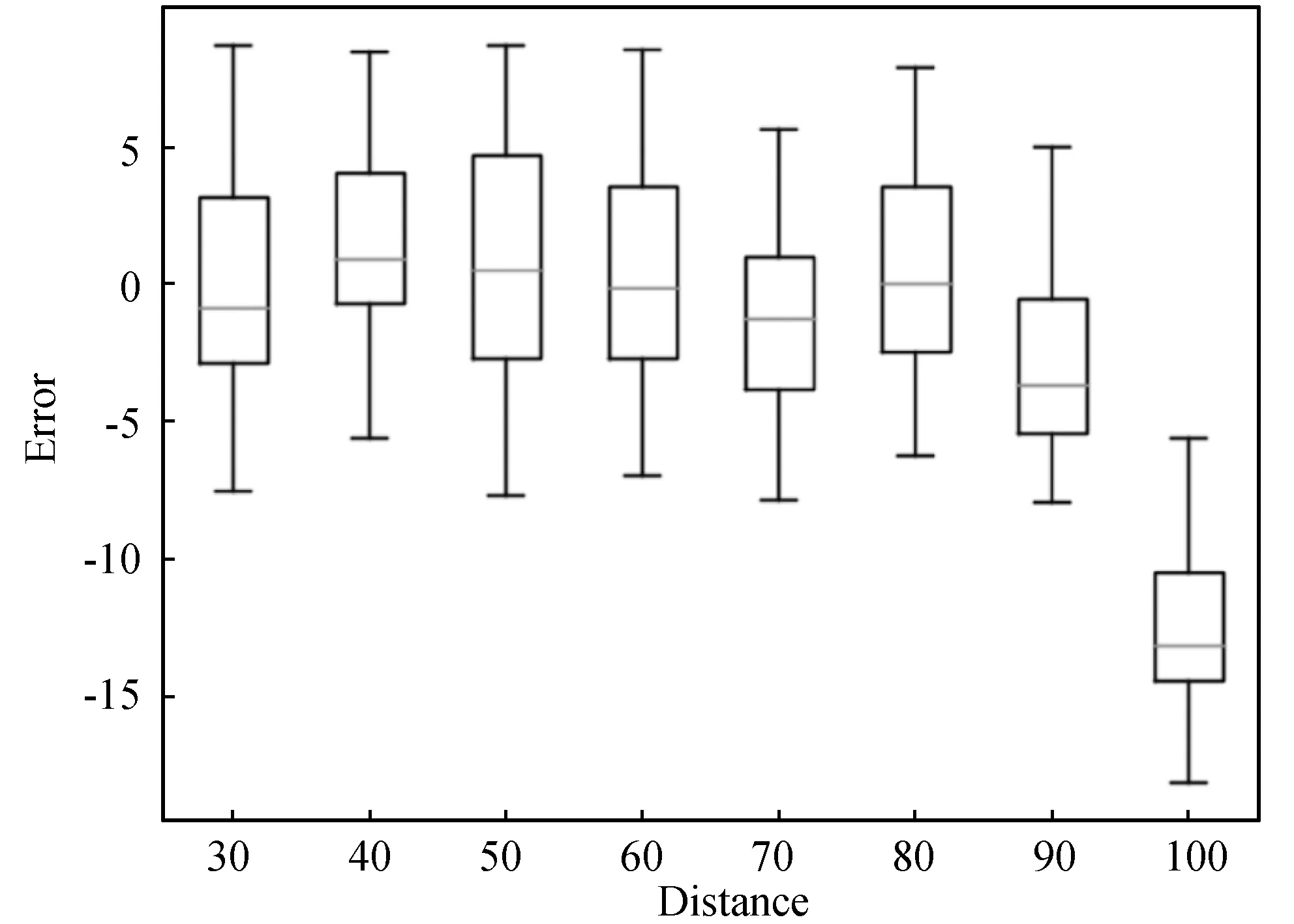
(b) 坐标系偏移修正后图5 数据集B测量值误差与距离关系

可见在进行坐标系偏移修正后，一方面能有效降低固有测量误差，另一方面误差的分布规律也更为明显。通过观察测量误差分布规律，有助于设计具有针对性的校正模型，从而提高校正精度。

3.2 模型结构

通过观察两个数据集中测量值误差的分布规律，可以发现EMTS的测量误差与距离、测量点所处象限等因素有关，其全局分布规律并不明显，因此不宜采用基于单BP神经网络模型的全局拟合方法[14]。本文对系统工作空间进行划分，针对局部空间使用单独的BP神经网络模型进行校正，通过设计集成学习模型来实现全局空间坐标校正。主要算法流程如图6所示。

图6 空间坐标校正算法流程

常见的集成学习模型有bagging、boosting、stacking等[19]。但本文同时使用两种采样方法，建立两个不同数据集来分别预测坐标值与距离值，因此本文采用类似双流模型[20]的结构，通过对同一输入对象提取不同类型的特征，再将基于不同特征得到的计算结果进行融合，来提高空间坐标的校正精度。

3.3 特征缩放

在使用BP神经网络对测量坐标值进行校正前，需要对输入特征进行归一化操作，使得所有样本的特征值都处于同一量纲下。EMTS的测量值包含X、Y、Z三个轴向的坐标值，在步骤1中引入坐标值的高次项xiyjzk，其中i,j,k=0,1,2，…，n,且i+j+k>1，从而丰富输入数据的特征。有别于机器学习分类问题中的规范化处理方法，本文根据空间坐标取值范围，采用小数定标标准化方法。

3.4 生成模型池

通过观察图4、图5可以发现，数据集A与数据集B中的误差分布呈现出显著的局部差异特点。因此，本文针对局部数据构建结构简单的子网络模型，在准确提取局部数据分布规律的基础上，通过构建模型池来实现全局数据的准确校正。

在选择BP神经网络模型结构时，在满足空间坐标校正精度的前提下，为保证系统的实时性，尽可能选择结构简单的子模型。数据集A中的BP神经网络子模型具有3个输出单元，对应校正后的3个坐标值；数据集B中的子模型具有1个输出单元，对应预测的距离值。

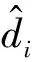
(1)

3.5 校正结果融合

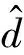
(2)

4 新场景快速评估

由于EMTS易受工作环境影响，若采样环境与实际工作环境不同，则有可能导致已采集的样本无法反映实际测量值的分布情况。但若每次部署到新场景中都使用较为繁琐的均匀离散采样方法进行重采样，则会降低工作效率。因此，本文提出一种在新场景中的快速评估与校正的方法，主要流程如图7所示。

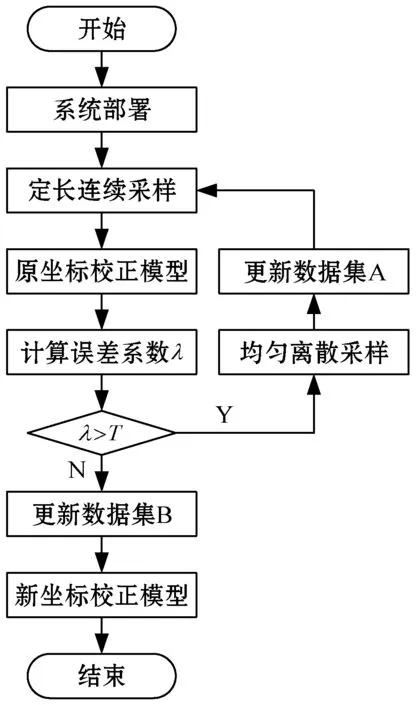
图7 新场景评估与校正策略

当系统被部署到新场景中后，首先使用快捷的定长连续采样方法在系统工作空间内进行采样。假设原三维空间坐标校正模型为M，则校正后的三维坐标值P′(x′,y′,z′)可表示为：

P′(x′,y′,z′)=M[P(x,y,z)]

(3)

可计算得到校正距离d′与已知真实距离d之间的误差:

(4)

定义误差系数为：

(5)

当λ大于预设阈值T时，表明当前工作环境与均匀离散采样环境存在显著差异，需要重新进行采样操作。反之表明因工作场景改变带来的误差较小，通过更新数据集B，可在本文校正算法的融合过程中实现自适应补偿，提高系统的抗干扰性能。

5 实验结果与分析

5.1 空间坐标校正效果

本文使用以Tensorflow为后端的Keras框架进行开发，所有BP神经网络子模型都使用ReLU作为激活函数；为避免模型过拟合，使用参数为0.001的L2正则化器；为加快训练速度，设置Batch size为64；使用Adam优化器动态调整参数学习率；使用均方误差MSE作为损失函数进行训练。

对于数据集A，根据坐标值x所处象限与距离d的大小对样本空间进行划分，分别训练子网络。由于目前对BP神经网络隐藏层的层数L与每层包含神经元的个数U如何设置还尚无定论，因此本文将特征缩放指数n=1,2,3，L=1,2,3，U=4,8,16,32,64,128进行排列组合，分别训练子网络，并选取其中校正精度最高的子模型构成模型池A，计算结果如表2所示。

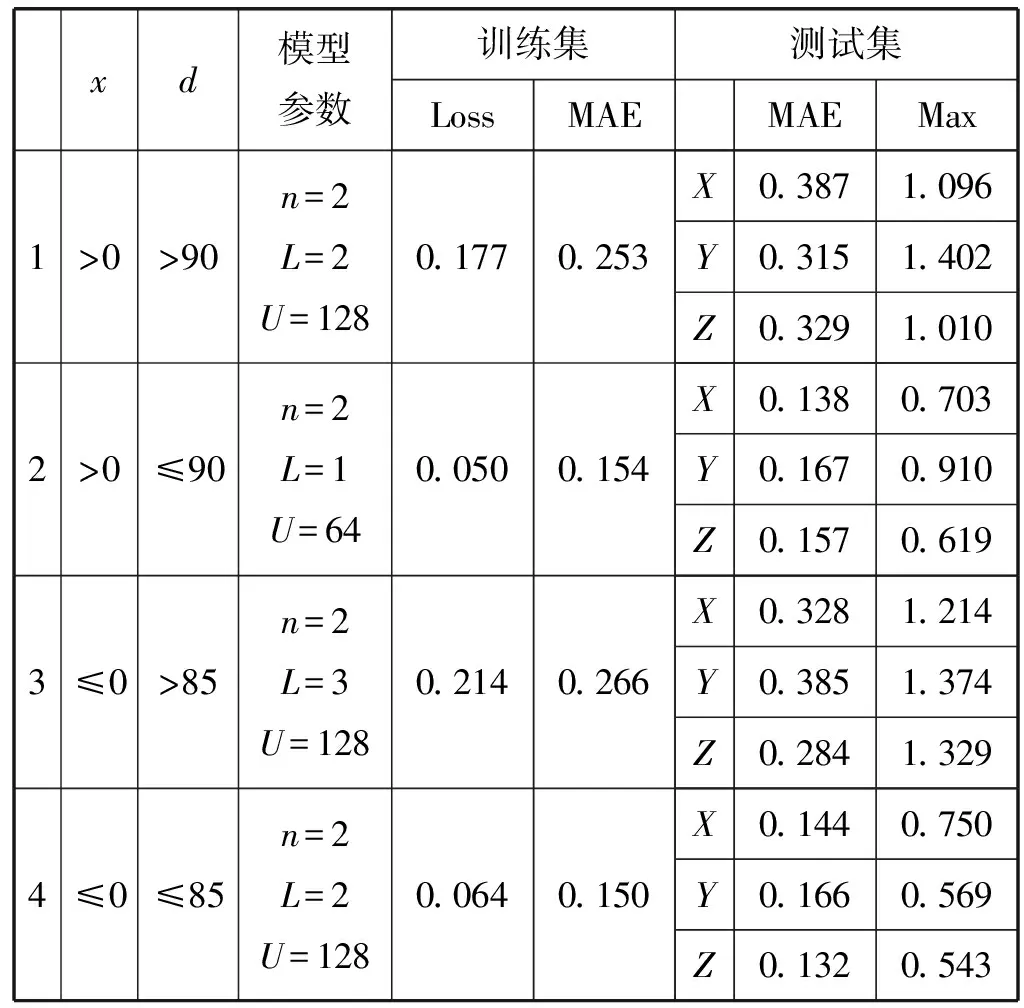
表2 模型池A子模型信息

同理，对数据集B，对整个数据集与不同距离d下的子样本集，在不同模型参数下进行训练，选取其中性能最好的子模型构成模型池B，计算结果如表3所示。

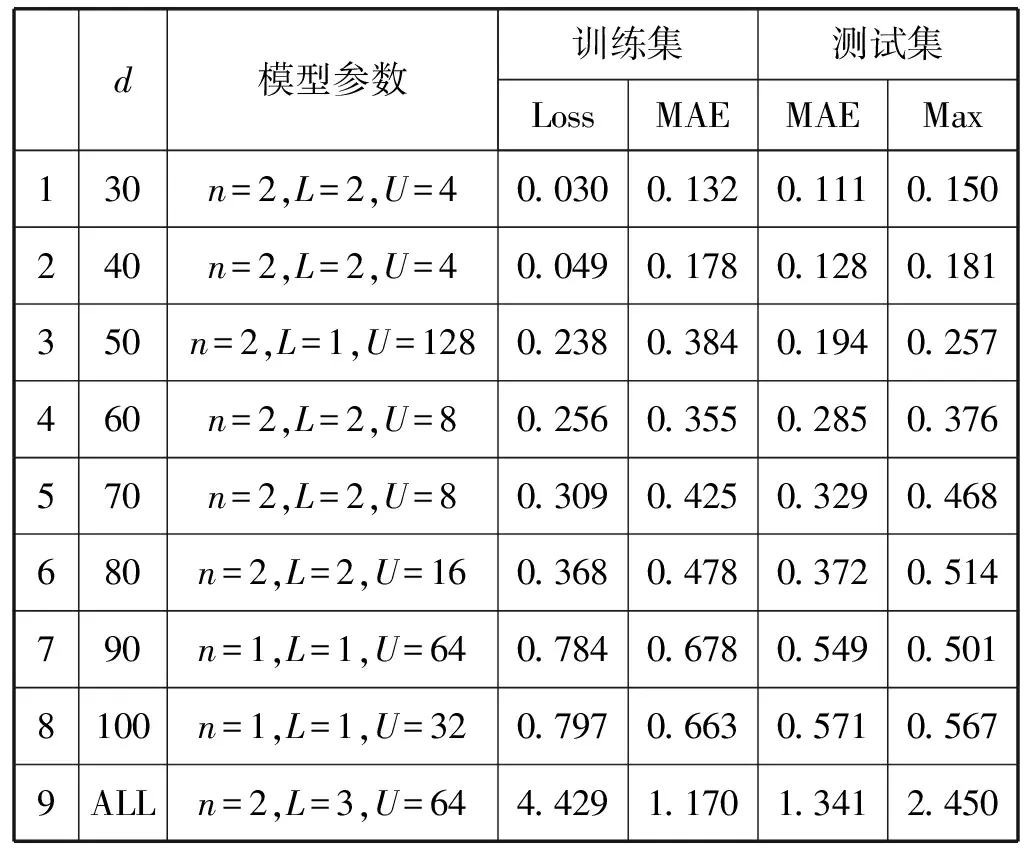
表3 模型池B子模型信息

与仅使用数据集A，采用n=2，L=3，U=128的单BP神经网络模型进行全局训练校正相比，本文采用集成学习方法能取得更高的校正精度，计算结果如表4所示。

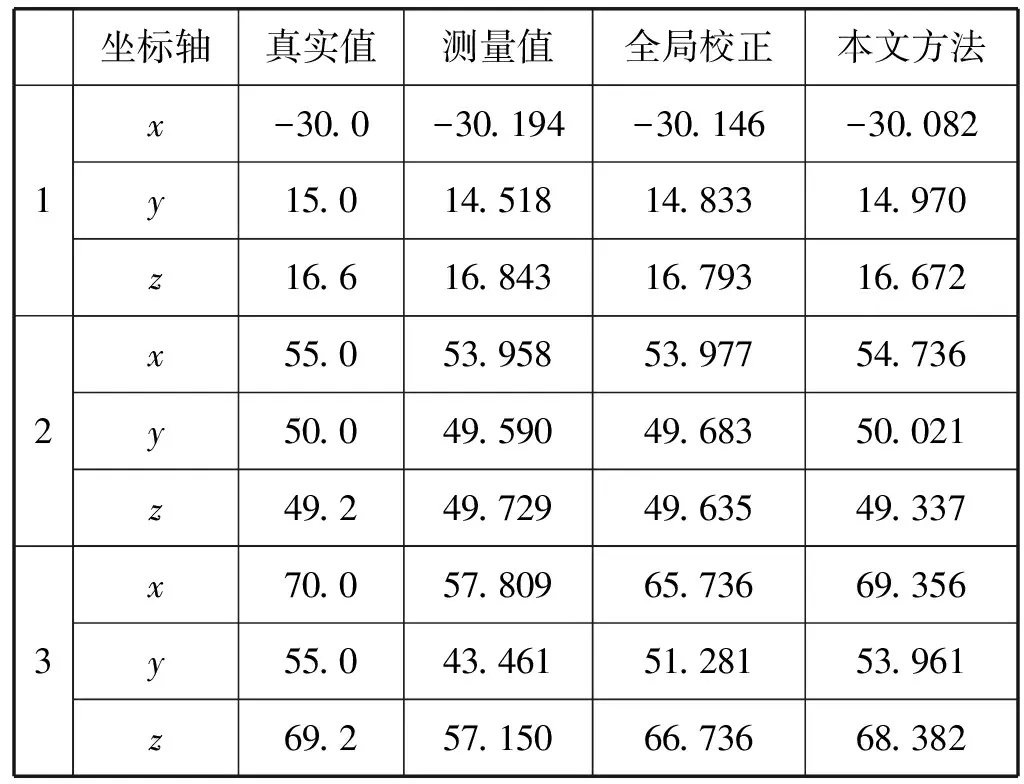
表4 本文算法空间坐标校正结果

5.2 新场景评估

为验证本文评估方法的有效性，在系统工作空间测量点附近放置金属干扰物，使得该测量点的测量值发生一定程度的偏移，然后再使用本文方法对其进行校正，效果如表5所示。可见在系统工作环境中加入干扰后，本文算法依然能得到与原工作环境相接近的空间坐标校正结果，表明本文方法具备一定的抗干扰能力。

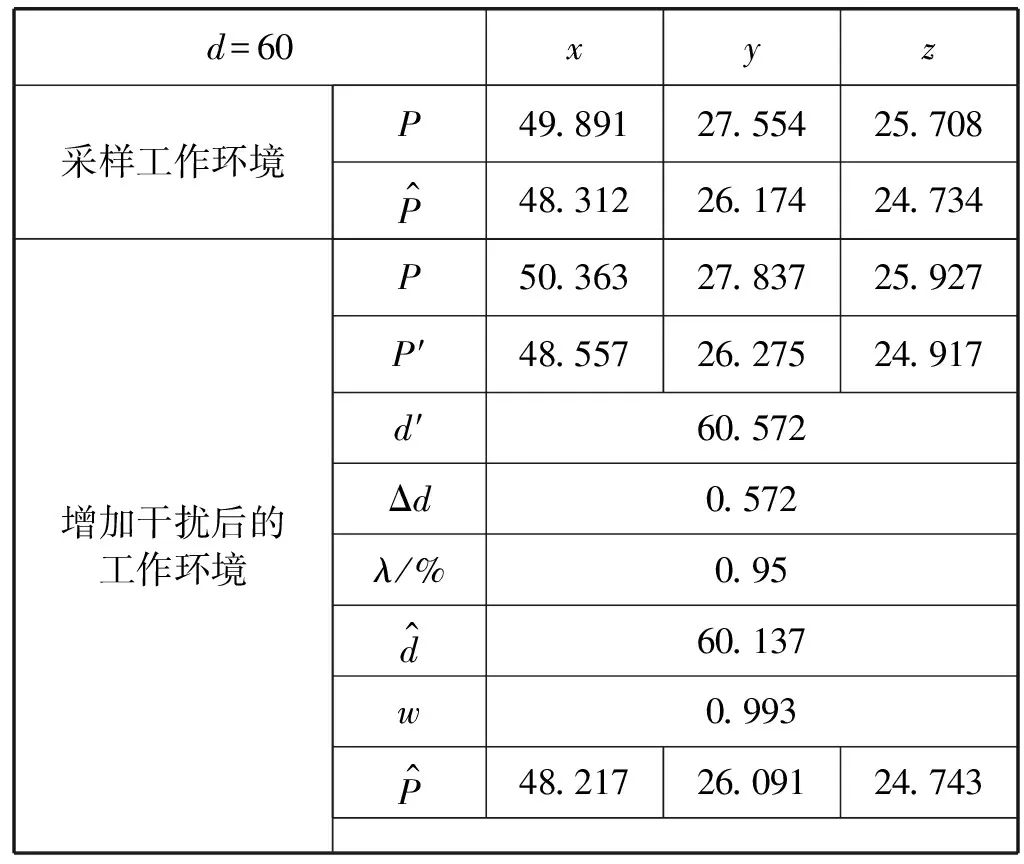
表5 本文算法抗干扰能力实验结果

本文系统中，T=1%，即当接收传感器距离发射源1 m时，其校正距离的误差应不大于1 cm。由于校正误差与距离呈正相关，而用于跟踪用户手部动作的传感器与发射源距离较近，其校正误差为毫米级，能满足AR系统中人机交互的精度需求。

5.3 系统运行效果

为验证本文算法对EMTS三维坐标的校正效果，搭建了一套AR交互系统，系统结构与设备连接如图8所示。该系统使用Ascension公司的Flock of Birds电磁跟踪系统，采用单发射源与3层级联控制器的工作模式。其中，安装于头部的接收器用于跟踪用户头部姿态，配合光学透视显示器实现虚实融合效果；安装于数据手套上的接收器用于跟踪手势轨迹，配合数据手套用于识别用户的交互手势。

图8 增强现实系统结构与设备连接

系统运行效果如图9所示。其中：图9(a)为系统初始状态，可以看到虚拟坐标系的原点与世界坐标系的原点能完全重合；图9(b)表明在视角改变的情况下系统能实现准确的虚实融合效果；图9(c)为第三视角下用户的交互过程，系统能正确识别用户手势操作与虚拟物体实时交互。

(a) 系统初始状态 (b) 第一视角 注册效果 (c) 第三视角 交互过程图9 系统运行效果

6 结 语

本文针对EMTS空间坐标校正问题，提出了一种定长连续采样方法，设计了基于BP神经网络集成学习模型的空间坐标校正方法，并提出一种EMTS在新场景部署过程中的快速评估方法。实验结果表明，本文方法能有效提高空间坐标的校正精度，能满足AR系统的跟踪注册要求，并能在一定程度上克服场景差异带来的误差，提高了系统的抗干扰能力。