Optimum structural design of full-scale steel buildings using drift-tribe-charged system search

Siamak Talatahari , Hedayat Veladi, Mahdi Azizi, Ali Moutabi-Alavi and Salar Rahnema

1.Department of Civil Engineering, University of Tabriz, Tabriz 51666, Iran

2.Faculty of Engineering and Information Technology, University of Technology Sydney, Ultimo, NSW 2007, Australia

Abstract: In this paper, the potential of utilizing improved metaheuristic approaches in optimal design of building structures is concerned.In this regard, the drift-tribe-charged system search algorithm is proposed that the position and velocity updating processes of the charged system search is developed by implementing the mathematical presentation of the free-electron model utilized for metal conductors.In addition, the searching phase of the developed algorithm is also divided into three separate phases in order to improve the convergence capability of the algorithm.By means of these modifications,the exploitation and exploration rates of the standard algorithm are enhanced.In order to determine the ability of the proposed improved metaheuristic method considering some complex optimization problems, a 10-story steel building structure with 1026 structural members alongside a 60-story structure with 8272 members are utilized as numerical examples.The overall capability of the developed metaheuristic approach is compared with other metaheuristics.A total number of 30 independent runs have been conducted for each of the standard and proposed methods while a statistical analysis is also conducted for comparative purposes.The obtained optimum results demonstrated that the proposed metaheuristic approach is capable of preparing better outcomes than other metaheuristics.

Keywords: drift-tribe-charged system search; optimum structural design; full-scale steel building; statistical analysis

1 Introduction

Trial and error is a common procedure for structural design purposes which is utilized by structural designers in most of the cases.Using developed computer programs alongside the fully-established computers results in high speed design of full-scale structures with great number of elements; however, finding an optimal and affordable selection of elements for a structure still requires multiple controls.Since it is a time-consuming and complex process, controlling all the possible scenarios in order to achieve the most optimal structural system by trial and error method is impossible.Therefore, optimization methods should be used to resolve this issue.

Classical methods of optimization require a huge amount of gradient data while these is a higher probability of converging to a local optimum solution which can be remarkably far from a desirable global solution.These kinds of concerns about the classical algorithms have resulted in a new methodology named “Metaheuristic”that is composed of “Heuristic” as the main word originated in Greece with a definition of discovering new strategies and “Meta” as a suffix with meaning of upper levels.Metaheuristics are some sorts of well-designed searching techniques that are capable of implementing higher-level tactics into searching processes in conducting optimization procedures for specific purposes.Many metaheuristic optimization algorithms have been used to optimal design of different types of structures.Hamzaet al.(2003) presented design optimization of multiple N-shaped truss structures using three different implementations of genetic algorithms (GA) alongside a developed version of taboo search (TS) method called reactive taboo search (RTS).Seyedpooret al.(2011)introduced an optimization procedure by simultaneous utilization of the particle swarm optimization (PSO)and perturbation stochastic approximation (SPSA),termed as SPSA-PSO, to determine the optimum shapes of arch dams determining the fluid-structure interaction effects subjected to earthquake effects.Omkaret al.(2011) developed a multi-objective generic method based on vector evaluated artificial bee colony(ABC) algorithm for intelligently optimum designing of composite components which are laminated.Sonmez (2011) utilized the ABC algorithm for weight minimization of truss structures by consideration of an adaptive constraint handling approach based on penalty functions.Kaveh and Talatahari (2012) used chargedsystem search (CSS) algorithm for optimum design of different frame structures.Kaveh and Ahangaran (2012)presented a social harmony search (HS) algorithm for cost optimization of composite structural floor systems with discrete optimization variables.Khatibinia and Khosravi (2014) proposed a hybrid metaheuristic approach by combination of the orthogonal crossover(OC) and an improved version of gravitational search algorithm (GSA) for shape optimization of concrete gravity dams.Kavehet al.(2015) utilized the improved magnetic CSS (IMCSS) and improved scheme of HS algorithm for optimal configuration of truss structures.Dede and Ayvaz (2015) used teaching-learning-based optimization (TLBO) algorithm for shape optimization alongside size configuration of different structures.Kaveh and Mahdavi (2015) developed a hybrid search technique based on colliding body optimization and PSO for optimal design of different structures under frequency constraints.Bekdaset al.(2015) discussed weight minimization of different truss structures by using flower pollination algorithm (FPA).Tokluet al.(2020) proposed total Potential optimization using metaheuristic methods (TPOMA) as a novel technique for nonlinear structural analysis which can be utilized with different metaheuristic algorithms for optimization purposes.Kayabekiret al.(2020) proposed a novel hybrid approach with combination of the HS and the FPA algorithms for optimizing structural systems in which the TPOMA was utilized for nonlinear structural analysis.Bekdaset al.(2019) proposed an advanced configuration of TPMO for optimization purposes in which the hybrid implementation of FPA and Jaya algorithm (JA) were also utilized as the optimization technique.In addition, some other researches have also been conducted for optimum designing of engineering problems (Aziziet al., 2020, 2019a, 2019b; Talatahariet al., 2021; Talatahari and Azizi, 2020a, 2020b, 2021).

Alongside the efforts in optimization of steel building structures, some of the metaheuristics were also utilized for finding optimum design of reinforced concrete structures.Nigdeliet al.(2018) utilized HS,TLBO and FPA for optimum design of reinforced concrete footings.Ulusoyet al.(2018) investigated the optimal design of multi-span, multi-story reinforced concrete structures with utilization of the HS algorithm in which the static loads were considered.Nigdeli and Bekdas (2017) proposed a random search technique(RST) for optimum design of reinforced concrete beams with consideration of unfavorable distributed live loads.Nigdeliet al.(2015) proposed a novel implementation of the HS algorithm in optimum design of biaxially loaded reinforced concrete columns.

Some other challenges in utilization of metaheuristics in different engineering applications were also investigated (Kaveh and Bakhshpoori, 2019).Chenet al.(2020a) proposed a hybrid metaheuristic approach for finding feasible self-equilibrium prestress modes of pin-jointed assemblies by combination of the PSO and symmetric schemes.Chenet al.(2021) utilized the PSO as the optimization algorithm for optimum design of non-trivial flat-foldable origami tessellations using 4 degrees vertices.Chenet al.(2020b) investigated feasible prestress modes in cable-strut structures in which the PSO was utilized as the optimization algorithm with consideration of multiple self-stress states.Kaveh and Talatahari (2010b) proposed an improved version of the ant colony optimization (ACO) for optimum design of planar steel frames.Chenet al.(2012)investigated prestress stability of pin-jointed assemblies by utilization of the ACO algorithm.Mölleret al.(2015) proposed a numerical optimization procedure for optimum configuration of structural design parameters with utilization of metaheuristic algorithms for optimum performance-based optimum design of office buildings.Zakian and Kaveh (2020) investigated topology optimization of structural shear walls with metaheuristic algorithms in which a simple penalty approach were was utilized for considering material and displacement constraints simultaneously.Parket al.(2018) utilized optimization algorithms for development of an optimum seismic retrofitting model for steel moment resisting structural frames in which the brittle connection were was utilized.Chunget al.(2009) investigated optimum design of tuned mass dampers with nonlinear viscous damping in which the feasibility of the research were was evaluated by implementing the optimum tuned mass dampers into the Taipei 101 tower.Yanget al.(2014)discussed optimum topology design of replaceable bar dampers in reticulated shells by utilization of using the incremental dynamic analysis.

The charged system search (CSS) as an efficient optimization algorithm was first introduced by Kaveh and Talatahari (2010a).This method utilizes some charged particles (CP) as solution candidates and moves these CPs in the considered search space in order to find the optimum solution.These movements comply with the governing of Coulom′s law from electrostatics and the Newtonian laws of mechanics.The main aim of this paper is to present an improved version of this algorithm termed drift-tribe-CSS and applying it for optimal design of real-scale building structures.In this improved metaheuristic approach, the velocity updating and position updating processes of the CSS is improved by implementing the mathematical presentation of the free-electron model utilized for metal conductors under the external electric field of finite temperature.In addition, the searching phase of the new algorithm is divided into three separate phases in order to improve the convergence capability of the resultant algorithm.These phases which are considered as tribes cause the algorithm to focus on global searching in the early iterations while the local searching is dealt with in the later iterations.This operation causes the algorithm to have an efficient exploration as well as a good exploitation experience.For evaluating the performance of the proposed drift-tribe-CSS method concerningcomplex optimization problems, a 10-story realsize building structure with 1026 structural members alongside a 60-story real-scale building structure with 8272 members are considered as design examples.In these building structures, the structural design sections are utilized as standard W-Shaped sections for structural members and the AISC-LRFD (2010) design code for steel structural design is utilized for consideration of the design requirements.

The remainder of this paper is consisting of a complete literature review on applications of the standard and improved versions of the CSS algorithm in the engineering optimization field, statement of the design optimization problem and description of the general and mathematical formulation of the CSS and the proposed drift-tribe-CSS algorithms.Afterwards,some frame structures as numerical investigations are being presented to provide a comparison among design procedures conducted by the drift-tribe-CSS, standard CSS and some other well-known algorithms.Finally, the numerical results and the concluding remarks are provided.

2 Literature review

In this section, a complete literature review on applications of the standard and improved versions of the CSS algorithm are provided in which the applicability of these metaheuristics in the engineering design optimization field is in perspective.

Kaveh and Talatahari (2010d) firstly utilized the CSS in optimization of truss and frame structures.They conducted a thorough comparing study of the outcomes of the CSS algorithm with other optimization algorithms and proved that the CSS provides very robust results.Kaveh and Talatahari (2010c) discussed the optimization of cross-sectional properties in transverse and longitudinal beams of grillage systems and studied the ability of the CSS in dealing with large scale engineering problems.Kaveh and Talatahari (2011a) developed a new approach based on CSS for optimization of dome structures with capability of determining automatically the number of elements and the element configurations during the optimization process.A discrete version of the CSS is developed by Kaveh and Talatahari (2012)in order to deal with the optimum design of frame structures.Kavehet al.(2012) utilized the CSS for optimum design of composite channels in which four different models were presented for design purposes.Kaveh and Behnam (2013a) discussed the optimum configuration of reinforced concrete cantilever retaining walls considering the static loads using the CSS.Kaveh and Behnam (2013b) utilized the CSS for optimum design of multi-story three dimensional reinforced concrete structures.Kaveh and Nasrollahi (2014)discussed the performance-based optimal seismic design of steel frames with the CSS optimization algorithm.Kaveh and Shokohi (2014) discussed the optimal design of castellated beam with the CSS method compared to some steel structural design codes and specifications.Kooshkbaghiet al.(2015) utilized the CSS for optimal topological configuration of geometrically nonlinear single layer latticed dome.Tavakkoliet al.(2016)presented the shape optimization of structures based on isogeometric analysis (IA) and sequential quadratic programming (SQP) methods utilizing the CSS algorithm.Sharafiet al.(2017a) presented a preliminary layout design of orthogonal buildings using the CSS algorithm.Sharafiet al.(2017b) discussed the free shape optimizations of thin-walled steel sections, represented by some popular graph theory-based methods using the CSS algorithm.Uzet al.(2018) utilized the CSS to formulate an automated technique for cost optimization of geometric configuration design of reinforced concrete beams with multi-spans excited by dynamic loading.

Kaveh and Talatahari (2011b) proposed the enhanced CSS (ECSS) with emphasis on the conception of fields of forces for global optimization.Kaveh and Zolghadr(2011) utilized ECSS in size and shape optimization of truss structures with some frequency constraints.Talatahariet al.(2014) studied the optimal design of industrial tunnel sections with the ECSS.Talatahari and Sheikholeslami (2014) utilized the ECSS in optimum design of reinforced and gravity retaining walls.Talatahariet al.(2011) combined the standard CSS with chaos (CCSS) to solve mathematical global optimization problems.Talatahariet al.(2012b) presented the complete methodology of the CCSS and its application in engineering design optimization.Nouhiet al.(2013a)utilized the CCSS for solving practical optimization problems.Kumar and Sahoo (2014) utilized the CCSS for data clustering and Nouhiet al.(2013b) discussed constraint optimization problems with this development.Talatahariet al.(2012a) combined the standard CSS with sub optimization mechanism (SOM) to improve the effectiveness and adaptability of this algorithm and mentioned the new method as the adaptive CSS (ACSS).Kaveh and Zolghadr (2012a) presented the improved CSS (ICSS) and utilized it in order to deal with the inverse problem of damage assessment in beams and frames.Saberi and Kaveh (2014) utilized the ICSS for structural damage identification.Kaveh and Zolghadr (2012b)discussed the damage assessment of truss structures with changes in mode shapes and natural frequencies using the ICSS.Kaveh and Zolghadr (2012c) also utilized the ICSS to deal with the problem of determining as many global optimum solutions as possible in a single run for damage detection of truss structures.

3 Optimum design of steel frames

3.1 Objective function

The main objective in optimization of building structures is to select proper design sections for structural elements in order to fulfill the required designobjectives and constraints.In this regard,Nddesign groups are considered and all of the structural elements(Nm) in the building are grouped into these groups.The solutions candidates in the optimization process are considered as some integer vectors which determines the required design sections for different elements while the objective function is considered to be satisfied based on the required design constraints.The overall weight of the structure can be determined as the objective function which is also utilized in this paper.The general formulation of an optimization problem considering the structural weight optimization is defined as follows:

where,ρirepresents the unit weight of the considered design sections (steel material in this paper) for theith design group;Aiis the length of the steel design sections for theith design group;Ntis the maximum required number of structural members for theith design group;andLjis the overall length of thejth structural element belonging in theith design group.

3.2 Design constraints

Considering the design requirements of the AISCLRFD (2010) for steel structural buildings, the structural strength and structural serviceability are determined as two of the main design requirement in these buildings.By considering the fact that the weigh minimization of the structures are considered in the optimization process,the following design constraints should be satisfied based on the strength requirements.

where,IELrepresents the number of structural members;Jis the considered load combination for design propose consideringNas the total number of required load combinations;PuJrepresents the required axial compressive or axial tensile strengths relating to theJth design load combination;MuxJandMuyJare the required flexural bending strengths considering theJth design load combination for the structural members relating to thexandyaxis considering the fact thatxandyare utilized for determination of strong and weak bending axis, respectively;VuJis the required shear strength relating to theJth design load combination;Pnis the nominal axial compressive or tensile strengths;MnxandMnyare the nominal flexural bending strengths relating to thexandyaxis, respectively;Vnrepresents the nominal shear strength;φrepresents the resistance factor for axial strength based on the gross section yielding in design sections which is 0.85 for compression strength and 0.9 for tension strength;φbrepresents the resistance factor for flexural strength which is set to 0.9;φvis the resistance factor for shear strength and it is set to 0.9.

Based on the gross sectional yielding of structural members, the nominal tensile strength is determined as follows:

where,Fyrepresents the considered specific yield stress for the structural elements in building andAgindicates the gross section for each of the structural elements.

The nominal strength for compression in the structural members are determined differently which have smaller values than the nominal tensile strength of these members due to the limited states of flexural buckling, torsional related buckling, and buckling of flexural-torsional state.The nominal strength for compression in the structural members regarding the limited states of flexural buckling of non-compact and compact design sections is as follows:

where,Fcrrepresents the critical stress based on the states of flexural buckling in design sections and is determined as follows:

where,lindicates the laterally unbraced length of structural elements;kis the members′ effective length factor;rrepresents the radius of gyration of designsections based on the buckling axis of sections;Eis the modulus of elasticity of the considered design material.

For the structural design sections that are doubly symmetric while the twist is considered around the shear center, the nominal strength for compression based on the limited states of torsional and also flexural-torsional buckling are determined as follows:

where,Cw,G,JT,Iz,Kz,IxandIyindicate the wrapping constant of design sections, shear modulus of considered steel material, torsional constant of design sections,unbraced length considering the torsional buckling,effective length factor in the torsional buckling, and moments of inertia considering the principal axes asxandy, respectively.

Based on some specific factors such as the local buckling in flanges of design sections, limited states of material yielding, local buckling in web of design sections, and the lateral-torsional buckling of structural elements, the minimum states of nominal flexural strength in structural members is determined as follows:

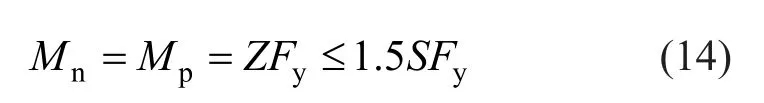
where,Sconsiders the design section modulus which is determined based on the bending axis of sections andZrepresents the modulus of plasticity considering the utilized steel material.The flexural capacity of structural elements regarding to the lateral-torsional limit states of buckling considering the doubly symmetric design sections is as follows:

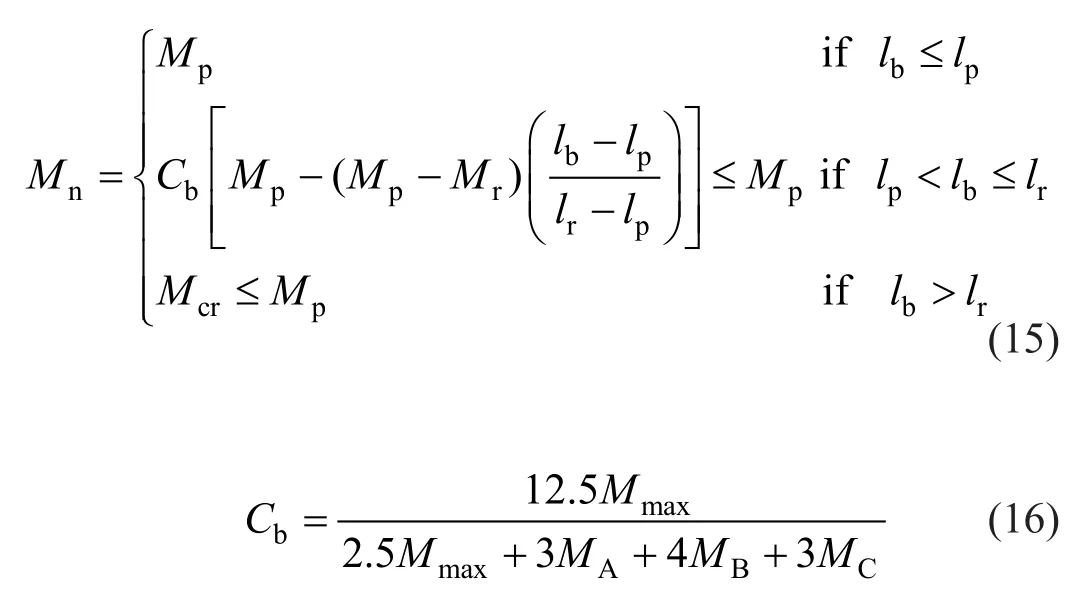
where,lb,lp,lr,Mr,Mcr, andCbare the lateral unbraced length of the structural elements, limiting states of lateral unbraced length considering the complete bending capacity in plastic states, limiting states of lateral unbraced length based on the inelastic lateraltorsional buckling of structural members, limited states of buckling moment, critical moment considering elastic lateral-torsional buckling states and the moment modification factor utilized for correction of the moment diagram which are distributed non-uniformly.Mmax,MA,MB, andMCare the absolute moments represented as maximum moment on structural members, moment in the quarter point of structural members, moment in the centerline of structural members, and the moment in the three-quarter of the unbraced length of structural members, respectively.

Considering the doubly symmetric design sections with non-compact flanges, the nominal flexural strength of structural elements based on the limit states of local buckling in flanges is determined as follows:

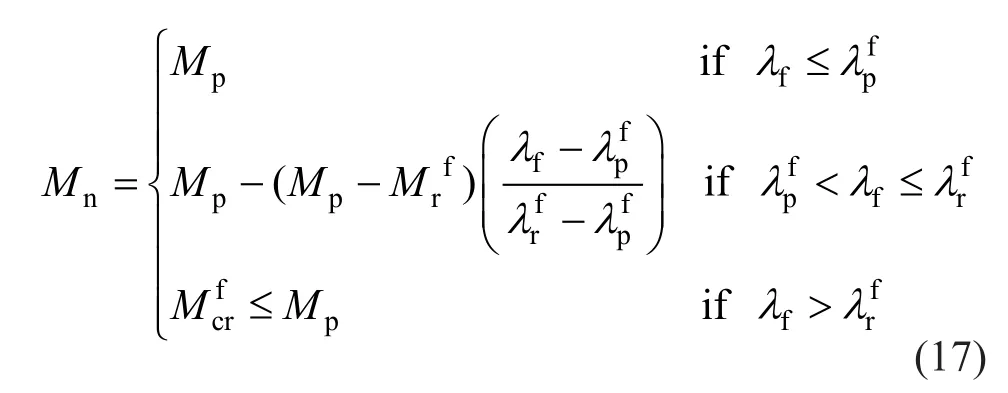
where,λfrepresents the flange slenderness withas the limiting state considering the total bending capacity in the plastic state of steel material andas the limiting state considering the flange local buckling in inelastic buckling state;represents the limiting moment based the buckling of flanges; andrepresents the critical moment based on the local buckling of flanges in elastic buckling state.

Considering the doubly symmetric structural design sections with non-compact webs, the nominal flexural strength of structural elements based on the limit states of local buckling in webs is determined as follows:

where,λwrepresents the web slenderness withas the limiting state considering the total bending capacity in the plastic state of steel material andas the limiting state considering the web local buckling in inelastic buckling state;represents the limiting moment based the buckling of webs; andrepresents the critical moment based on the local buckling of webs in elastic buckling state.

Considering the doubly symmetric structural design sections assigned to shear force directly to the plane ofthe web, the nominal strength for shear in the unstiffened webs of the design sections is determined as follows:

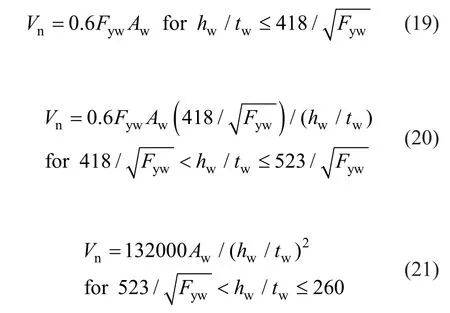
where,hwindicates the clear total distance among flanges of design sections which is considered by omitting the corner radius or fillet in dealing with rolled design sections;twindicates the total web thickness of design sections;Awrepresents the shear area of sections; andFywconsiders the yield stress of web in design sections.

In order to calculate the effective length factor (K) of structural members which is untitled for considering the nominal compressive strength of the structural elements,the following equations are determined for each of the structural joints:

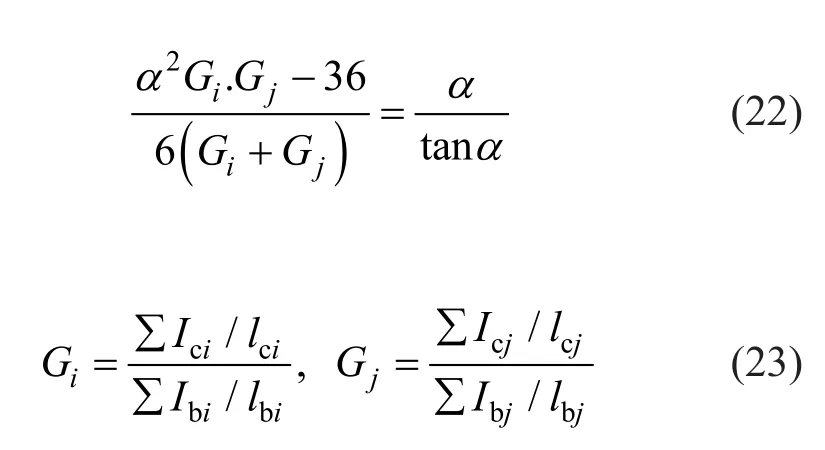
where,iandjare utilized as subscripts related to theith andjth ends of the structural member which is considered as compressive elements; b and c are utilized as subscripts related to the beams and columns which are connected to the considered structural joint;Irepresents the moment of inertia for the considered design section;lindicates the unbraced length of the structural member;αis determined as a parameter which is set to π/KwhileKis a factor for considering the structural resisting systems such as bracings and moment resisting frames.

The serviceability of the considered structural building should be satisfied based on the displacement factors which are determined as follows:

4 Utilized optimization algorithms

In this part, the general and mathematical formulation of the drift-tribe-CSS as an improved metaheuristics algorithm is described while a brief description for the standard CSS algorithm is also provided.

4.1 Charged system search

In the standard CSS method, each solution nominee(Xi) is consisting of decision variables (i.e.,Xi={xi,j})that is known as a charged particle (CP).Each CP is affected by the electrical fields from other CPs by exerting electrical forces.By utilizing the well-known electrostatics laws alongside the Newtonian mechanics laws, the quantity of this force and the quality of particles′ movement are determined.It seems that a CP with better position must exert a stronger force than the CP placed at a bad position.In this regard, the amount of the charge can be determined by calculating the values of objective function for the CPs.

In order to use the CSS as an optimization algorithm for optimization problems, some of the important aspects of the algorithm are mentioned.

In the CSS, a number of CPs with special magnitudes of charge (qi) that provides an electrical field around its position is considered.Determining the quality of each CP, the related charge magnitude is defined as following:

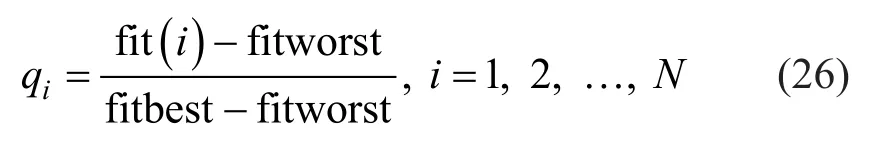
where, fitbest and fitworst are the best and worst fitness between all CPs;fit(i)is the fitness value obtained by the objective function for the agenti, andNis the maximum number of considered CPs.rijis the separation distance considered between two CPs and is calculated as following:

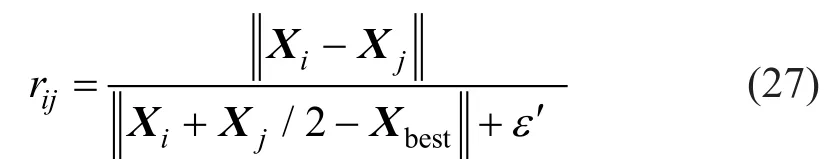
where,XiandXjare the position vectors of theith andjth CPs, respectively;Xbestis the position vector of the current best CP, andεis a vector with small positive numbers for singularity issues.

By utilizing a random process, the initial positionvectors of CPs in the search space are determined and the initial velocity vectors of CPs are considered to be zero.In the CSS, all CPs with better positions can attract CPs with bad positions and only a small number of the CPs with bad results can attract CPs with good results.The mathematical presentation of the resultant electrical force relating to a CP is considered as follows where the resultant force relating to thejth CP, are depicted in Fig.1.

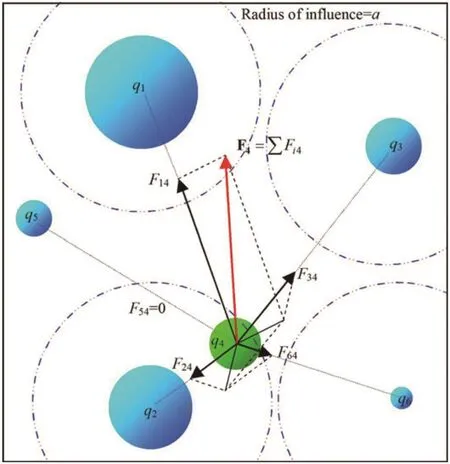
Fig.1 The process of determining the resultant electrical force exerted on a CP (Kaveh and Talatahari, 2010a)

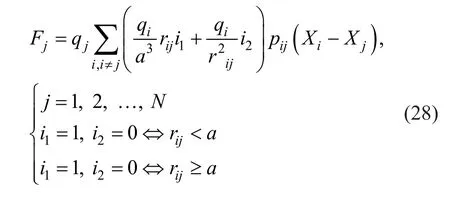
For each CP, the new position vector alongside the new velocity vector are determined as follows:

where,kaandkvrepresent the acceleration and velocity coefficient, respectively.randj1andrandj2are two random vectors which are distributed uniformly in the number range of (0, 1).The moving process of a CP to its new position is illustrated in Fig.2.

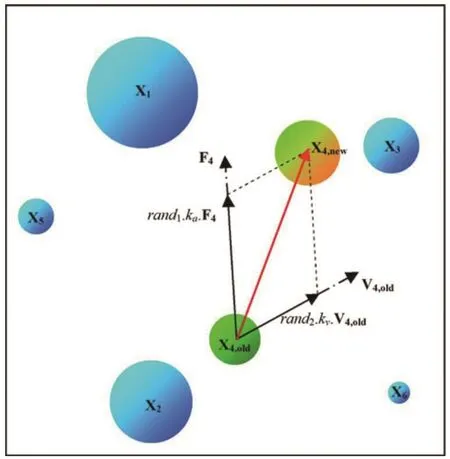
Fig.2 The schematic view for a CP moving to a new position(Kaveh and Talatahari, 2010a)

In the CSS, a memory in which the position of overall best CPs and the related objective function values are determined for enhancing the capability of the CSS algorithm.The mentioned memory is represented as the charged memory (CM) and a specific number of the best CPs among the so far found solution candidates are saved on it.The overall size of the CM in this paper is considered asN/4.

4.2 Drift-tribe-charged system search

The main improvement concept for the drift-tribe-CSS algorithm is derived of the free-electron model utilized for metal conductors under the external electric field of finite temperature.By applying a potential difference to a conductor, the electrons which are free in the field tend to gain or lose velocity in the opposite or similar direction to the electric field among successive collisions.In this regard, there should be another velocity component in addition to the random thermal velocity which is called “drift velocity” in order to represents the movement of electrons.In other words,the random movement of free electrons is modelled by superimposition of drift velocity on the random velocity of free electrons.The mathematical presentation of these points are provided in the following:

where,Vis the electron total velocity;Vris the random velocity andVdis the drift velocity.Therefore, the velocity updating process of the CSS algorithm presented in Eq.(30) is modified by implementing the mathematical presentation of the free-electron model utilized for metal conductors under the external electric field of finite temperature.In this regard, theCas the mean of all solution candidates is considered as a position vector which includes the average of all CPs in the search space and is presented as follows:

where,Xiis the position vector forjth CP andNis the total number of CPs.

By considering the fact that the velocity of an electron is comprised of random and drift velocity,the velocity updating process for the CSS algorithm is determined as follows:

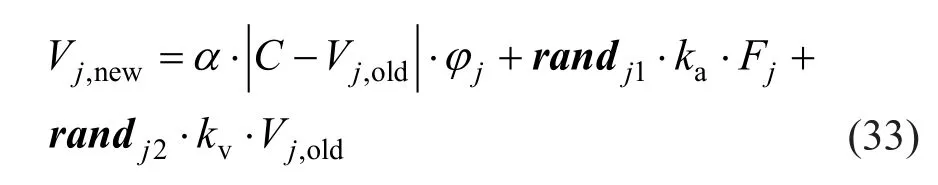
where,Cis the mean of all CPs;φiis a normally distributed random number;kaandkvrepresents the acceleration and velocity coefficient;randj1andrandj2are two random vectors which are distributed uniformly in the number range of (0, 1); andαis the convergence factor which is determined as follows:

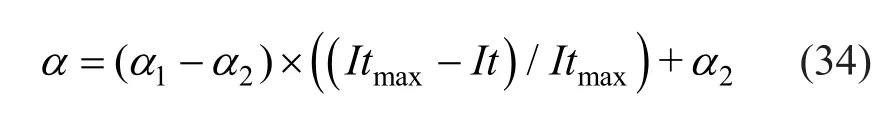
where,α1andα2are the initial and final values of the convergence factor which are determined randomly in the initialization phase of the algorithm;Itmaxis the maximum number of iterations;Itis the current iteration.

It should be noted that in this modification process for the CSS algorithm, the position updating is conducted by utilizing Eq.(29) while the velocity updating process is determined by utilization of Eq.(33) which is derived of the free-electron model utilized for metal conductors.

A premature and inappropriate convergence could be a probable outcome for most of the well-established optimization methods.In the last recent decades, there has been an interesting attempt in enhancing the overall capability of the metaheuristic methods and algorithms in which the capability of the algorithms in dealing with some difficult and complex optimization problems are enhanced by giving some proper approaches to the deficiencies of the algorithms.In this regard,another concept is proposed in this paper to improve the capability of the CSS method in dealing with engineering design optimization problems.This concept is derived of the fact that by separating the search space into multiple isolated ones called “Tribes”, the searching process is conducted in an old fashioned way in which the tribes are capable of providing a civilized way of living without communicating with each other in the early ages however for a better lifestyle, these tribes attempt to share information with each other and even merge with each other in the subsequent years.Based on the presented concept, the search space in the CSS algorithm is divided into multiple tribes in which the searching process in each tribe is conducted in a special way which improves the capability of the standard algorithm.

In order to mathematically present the mentioned concept, an integer number (Ntribe) as the maximum number of tribes should be defined which is utilized to allocate the solution vectors in the search space into these tribes.Each of the mentioned tribes includes a randomly determined number of solution vectors (Ns) in which the searching process is conducted in these tribes in a specific way.The main searching phase of the algorithm is divided into three distinctive phases as the isolated phase, communing phase, and the united phase.The stopping criteria is also adapted into the new formulation in which the maximum determined number of objective function evaluations or the maximum considered number of repeated iterations are divided into these three phases.

In the first phase of the algorithm specified as the isolated phase, the searching process is conducted in which the solution vectors in the search space and inside the CM are not permitted to share information or their distinctive experiences relating to other tribes.This step continues until the predefined stopping criteria which is divided into the mentioned three phases is reach.In the second phase as the communing phase, the tribes are permitted to use the solution vectors in the CM of each other and update their best so far found information.In the united phase as the third phase, all of the solution vectors in different tribes come to a unit tribe and this phase continues up until the predefined termination criterion is satisfied.In Fig.3, the pseudo code of the proposed drift-tribe-CSS algorithm is presented.

Fig.3 Pseudo code of the drift-tribe-CSS algorithm

5 Design examples

Based on the fact that the capability of the proposed drift-tribe-CSS should be evaluated in dealing with some complex optimization problems, two realsize building structures are selected for this purpose.These structural building have different characteristics including different plans and different heights in which the material properties for structural design sections are utilized as a steel withEas the modulus of elasticity equivalent to 200 GPa,Fyas yield stress equivalent to 248.2 Mpa, andρias the unit weight of steel material equivalent to 7.85 ton/m3.

In order to design the structural elements of the considered buildings, an overall number of 10 load combinations for design are determined based on the requirements of the ASCE/SEI7-10 (2010) which are described in Table 1.It should be noted that the acting loads on beam elements of typical floors are determined as 14 and 10 kN/m for dead and live loads, respectively while these values are 12 and 7 kN/m for the roof beams.

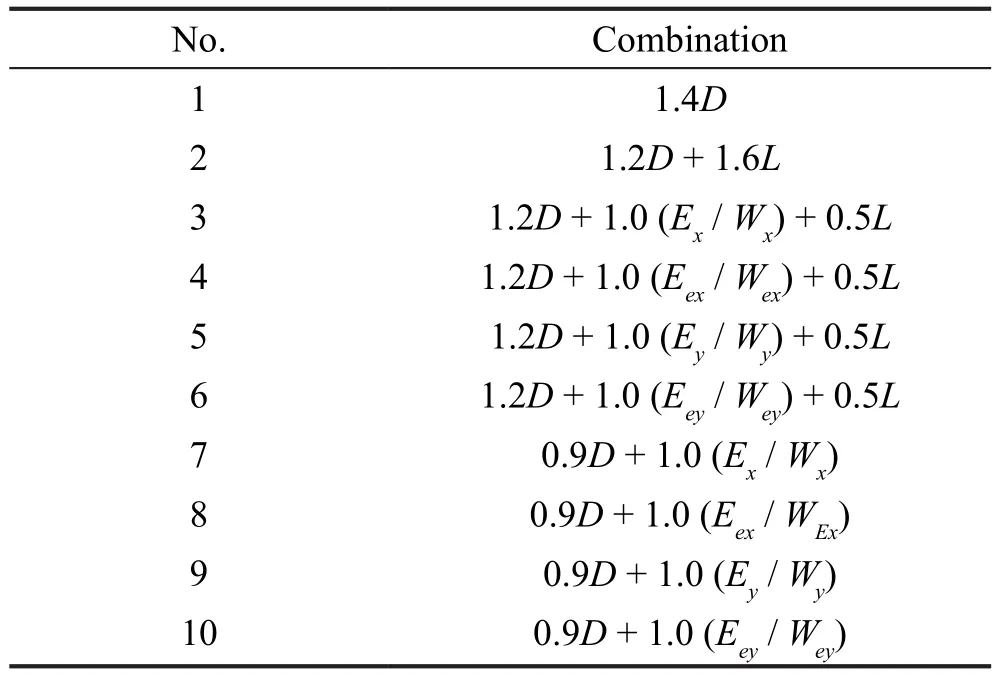
Table 1 Load combinations for structural design of steel design sections

5.1 Example 1: 10-story, 1026-member steel structure

The first design example is a 10-story steel structure which have 1026 structural members.This building structure consists of 350 column elements, 580 beam elements, and 96 bracing elements which should be designed with W-shaped steel design sections.The lateral resisting system of this design example is comprised of moment resisting frames alongside the cross bracingsystems.In Fig.4, the schematic and plan view of this building are presented while the elevation views in both of theXandYdirections are presented in Fig.5 and Fig.6, respectively.

Fig.4 Schematic view for the 10-story building structure

Fig.5 Plan view for the 10-story building structure (m)

Fig.6 Elevation views for the 10-story building structure (m)

For design purposes, the structural elements of different types should be grouped properly.In this regard,two kinds of grouping procedures are utilized in plan and elevation in which all of the structural members are grouped in every three stories in elevation levels except for the first story that is considered separately.Besides,beam elements are grouped as inner and outer beams in plan levels while the bracings are determined to be in one group in plan levels.For the column elements, the grouping process is presented in Fig.7.

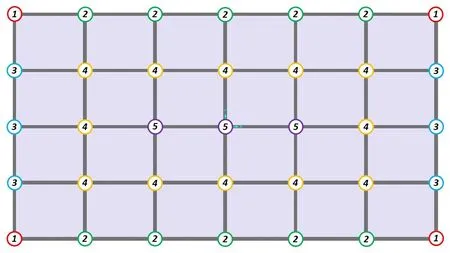
Fig.7 Column grouping procedure for the 10-story building structure

5.2 Example 2: 60-story, 8272-member steel structure

The second design example is a 60-story steel building structure which have 8272 structural elements.This building is consisting of 3960 column elements,3960 beam elements, and 352 bracing elements while the W-shaped steel sections are utilized as design sections.The lateral resisting system of this design example is determined as moment resisting frames with mega bracings for the first 24 stories while the moment resisting systems with standard bracing elements aredetermined for the 25th to the 60th stories.In Fig.8 and Fig.9, the schematic and plan view of this building are presented, respectively.

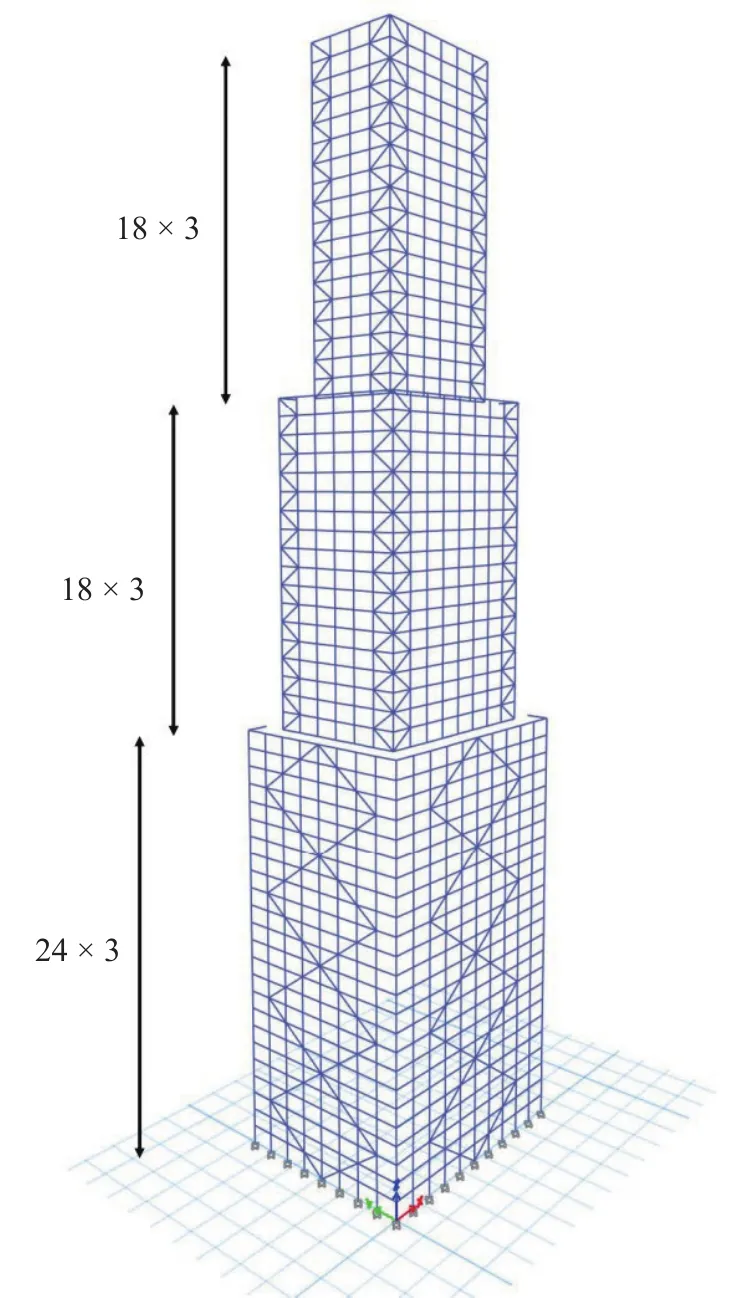
Fig.8 Schematic view for the 60-story building structure (m)

Fig.9 Plan view for the 60-story building structure (m)

Two kinds of grouping systems are determined for design purposes in plans and elevations of this building structure.In this purpose, the structural design members are all grouped in every six stories in elevation levels while the corner and side columns are grouped separately in each of the structural tubes as illustrated in Fig.10.In addition, the beams are grouped separately in each of the considered tubes while the bracings are considered in one design group.

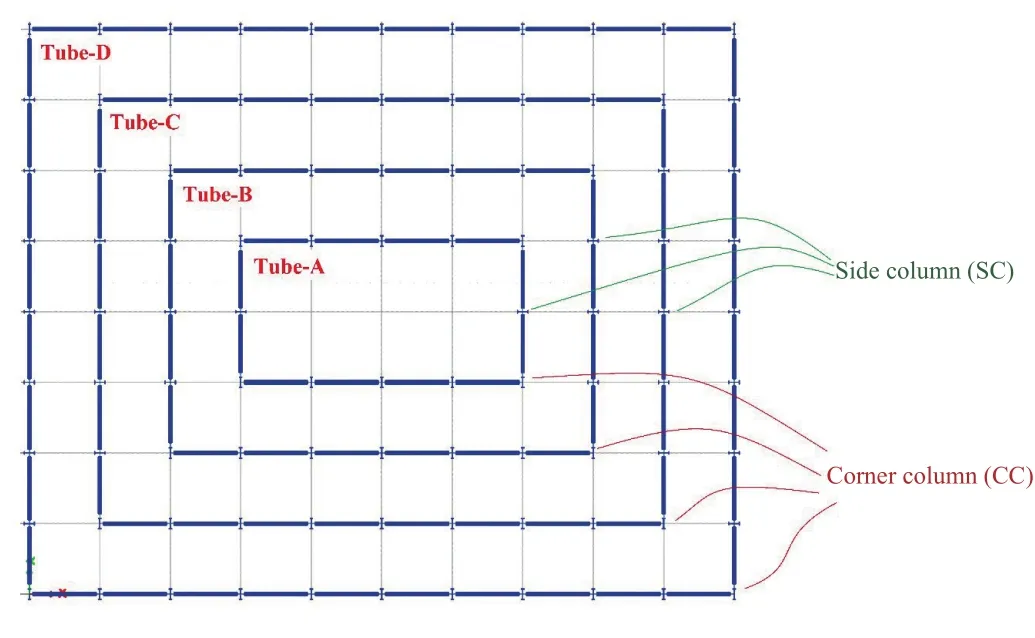
Fig.10 Grouping procedure for columns in the 60-story building structure

It should be noted that the selected design examples are modeled in the SAP2000 as one of the well-known structural design softwares and the final optimum designs obtained by the presented algorithm are also modeled in this software to check the constraints as well.The all reported results are confirmed by the SAP2000.

6 Numerical results

In this part, the obtained analytical results for the structural weight optimization procedure considering the previously described 10- and 60-story steel building structures are presented.A total number of 30 independent runs have been conducted for each of the CSS and the proposed drift-tribe-CSS methods.The convergence histories for the best results of the standard CSS and the drift-tribe-CSS algorithms for the 10- and 60-story structures are presented in Figs.11 and 12,respectively.It is obvious that the proposed drift-tribe-CSS method converges to some better solutions than the standard CSS algorithm with lower number of required structural analysis.

Fig.11 Convergence history for the CSS and drift-tribe-CSS(the 10-story building structure)

Fig.12 Convergence history for the CSS and drift-tribe-CSS(the 60-story building structure)

The optimum design sections for the best optimum results of the drift-tribe-CSS and the standard CSS algorithms considering the 10-story steel building structure are displayed in Table 2.Besides, the best results of the conducted 30 independent runs have been reported in this purpose.The total structural weight of the 10-story steel building structure determining the CSS standard algorithm is calculated as 549.18 ton while for the drift-tribe-CSS, the structural weight is obtained as 525.13 ton.It can be concluded that the total structural weight of this building structure determined by the drifttribe-CSS has lower value than the CSS which represents the ability of the proposed drift-tribe-CSS algorithm in reducing the overall weight of the structure.In Table 3,a comparative investigation based on the provided results by Azad and Hasançebi (2013) and Talatahariand Azizi (2020a) has been conducted which proves the capability of the drift-tribe-CSS in dealing with this design example.In this table, the best results of six other metaheuristics are provided in which the quantumbehaved developed swarm optimizer (QDSO) with 530.33 is the best one while the proposed drift-tribe-CSS algorithm is capable of calculating 525.13 which is even better than the QDSO.

Table 2 Optimal structural design sections for the 10-story steel building structure

The optimal design sections for the best optimal results of the drift-tribe-CSS and the standard CSS algorithms considering the 60-story steel building structure are displayed in Table 4.Besides, the best results of the conducted 30 independent runs have been reported in this purpose.The total structural weight for the 60-story steel building structure obtained by the CSS standard algorithm is obtained as 7042.88 ton while it is 6892.18 ton for the drift-tribe-CSS.It can be concluded that the total structural weight of this building structure determined by the drift-tribe-CSS has lower value than the CSS which represents the ability of the proposed drift-tribe-CSS algorithm in reducing the total weight of the considered structure.

For the 60-story budging structure, a comparative investigation has also been conducted in Table 5 based on the results of different recently proposed metaheuristics.Based on the results, the proposed drifttribe-CSS algorithm is capable of calculating 6892.18 which is the best among other five approaches while the maximum difference between this algorithm and the other metaheuristics is about 5% which is for Tiki-taka algorithm (TA) while the minimum difference is about 2% (CSS).

The statistical results obtained for the optimum design procedure conducted by the standard CSS method and the proposed drift-tribe-CSS methods based on 30 independent runs is presented in Table 6.It is proved that the developed drift-tribe-CSS algorithm is able of providing better analytical results than the standard CSS method by considering the mean and standard deviation results.The proposed drift-tribe-CSS is capable of calculating 552.17 and 7137.90 for mean values of 30 independent runs in 10- and 60- story buildings which are better than the results of CSS (601.21 and 7818.17).In addition, the standard deviation (Std.) of 30 independent runs for drift-tribe-CSS in 10- and 60-story buildings are 19.21 and 161.82 which are better than the results of CSS algorithm (38.17 and 418.25).

Table 3 Comparative results considering the 10-story building structure

Table 4 Optimal structural design sections for the 60-story steel building structure

Table 5 Comparative results considering the 60-story building structure

Table 6 Statistical results for the CSS and the proposed Drift-tribe-CSS methods based on 30 independent runs

The stress ratios in the structural members of the considered 10-and 60-story buildings considering the best results of the algorithms are provided in Figs.13 and 14, respectively for the CSS algorithm and the proposed drift-tribe-CSS algorithms.Also in Fig.15 and Fig.16, the maximum drift ratios in the considered 10-and 60-story buildings considering the best results of the algorithms are presented for the CSS algorithm and the proposed drift-tribe-CSS algorithms, respectively.It can be concluded that the higher values partially near to the allowable levels considering the drift-tribe-CSS

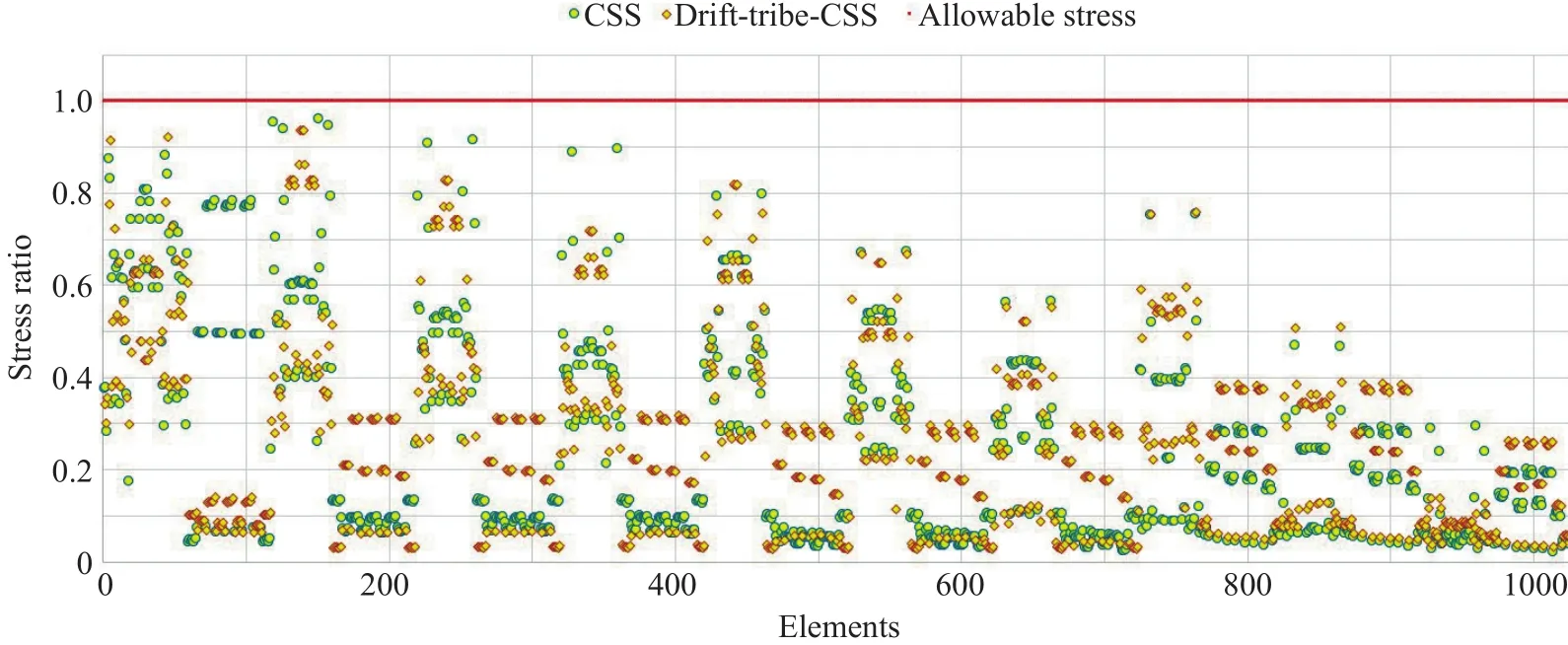
Fig.13 Stress ratio in the structural members of the 10-story building

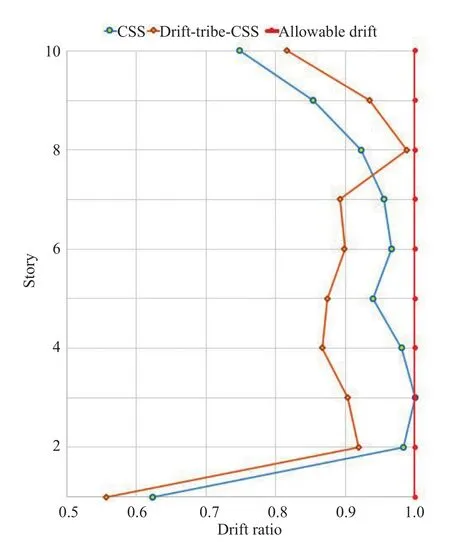
Fig.15 Drift ratio for the 10-story building

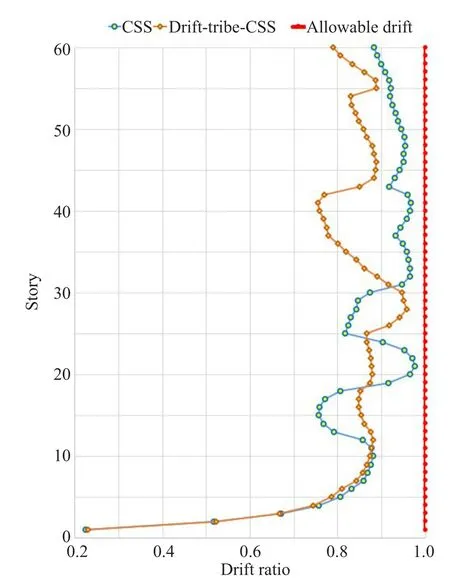
Fig.16 Drift ratio for the 60-story building

BESO: Bald eagle search optimization (Alsattaret al., 2020)SO: Sailfish optimizer (Shadravanet al., 2019)

GTO: Group teaching optimization (Zhanget al., 2020)TA: Tiki-taka algorithm (Rashid, 2021)algorithm which represents the potential of the proposed improved method in providing an economic design process.

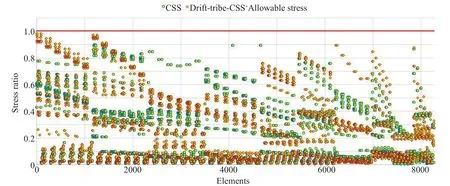
Fig.14 Stress ratio in the structural members of the 60-story building

7 Conclusion

In this research work, an enhanced metaheuristic optimization method represented as “drift-tribe-charged system search” is developed for optimal design of different steel structures.In the proposed method, the position and velocity updating processes of the CSS is developed by implementing the mathematical presentation of the free-electron model utilized for metal conductors under the external electric field of finite temperature.In addition, the searching phase of the standard algorithm is divided into three different phases.These phases which are considered as tribes cause the algorithm to focus on global searching in the first half of the iterations while the local searching process is dealt with in the later iterations.By means of these modifications,the exploitation and exploration rates of the standard algorithm are improved.According to the necessity of evaluating the performance of the proposed drifttribe-CSS optimization algorithm considering complex optimum design problems, a 10-story real-size building structure with 1026 structural members alongside a 60-story building structure with 8272 members are determined as numerical examples.The capability and performance of the proposed improved metaheuristic approach is compared to the CSS algorithm and some other metaheuristic algorithms.The results of the optimization procedures demonstrate that the developed drift-tribe-CSS method is able to calculate better results in dealing with the 10- and 60-story examples than the other metaheuristics.The total structural weight of the considered 10-story steel building structure is calculated as 549.18 ton using CSS and 525.13 ton using drifttribe-CSS that the reduction rate is around 5%.The overall weight of the 60-story steel building structure is obtained as 7042.88 ton using the CSS and 6892.18 ton using the drift-tribe-CSS that the reduction rate in this case is around 3%.In addition, the structural members have higher drift and stress ratios partially near to the allowable levels considering the drift-tribe-CSS algorithm which represents the potential of the proposed improved method in providing an economic design process.The major advantage of the proposed drifttribe-CSS is its capability in dealing with large search domains which is very critical in the considered 60-story building structure.Using such advanced algorithm is even important if nonlinear designing process is considered where the required time for performing a nonlinear analysis is very high compared to the linear one.By using the presented method, the required number of analyses for reaching an acceptable optimum design is less than other methods and as a result, it seems using such advanced methods becomes necessary.For the future challenges, this aspect can be investigated while the utilization of different materials for constructions purposes can also be investigated based on the fact that many new technologies are recently proposed in this area.

Acknowledgment

This research is supported by a research grant of the University of Tabriz (Number: 1105).