山区高速公路爬坡车道长度可靠性设计

张 航 涂智佳 田 晟* 曲路畅

(武汉理工大学交通与物流工程学院1) 武汉 430000) (宜昌市夷陵区交警大队2) 宜昌 443100 )

0 引 言

载重汽车因其爬坡能力不足造成的速度折减现象，对山区高速公路的道路通行能力和行车安全造成了很大的影响．其主要表现为：载重汽车在爬坡时的行驶速度降低过多，其速度与小型车的速度相差较大，容易发生车辆尾随相撞等交通事故．为了保证行车安全，各国采取的主要做法是设置爬坡车道，以此来把上坡路段速度降低过快的载重汽车分流到爬坡车道，保证其他车道正常的通行效率．梁国华等[1]构建适用于爬坡路段的交通流元胞自动机模型，分析超车行为车道数、坡度、坡长、车速、大车混入率等因素对爬坡路段通行能力的影响，单向双车道增设一条爬坡车道后，其通行能力可提高8%～16%．梁永东等[2-3]通过大量的车辆仿真实验，从安全和效率的角度说明了设置爬坡车道的必要性．陈芳等[4-5]通过在贵州省S102公路、姜眉公路眉太线采集大量车辆实际运行速度之后，确定需要设置爬坡车道的路段并计算了相关的坡度限制条件．

现有对爬坡车道的研究主要集中在其设置有效性上，对其长度计算并未有确切的方法．实际设计及施工过程中，主要依靠设计人员的主观经验进行判断．鉴于近年来公路几何设计中开始使用可靠度理论，如Navin等[6]最先将可靠性理论引入到道路工程中去，基于可靠度计算高速公路临界坡长.引入可靠度设计理念进行道路优化和安全分析等．因此，考虑到车辆爬坡中运行速度变量具有统计意义，且服从概率分布，满足可靠度应用的条件，本文将可靠度理论与爬坡车道长度设计结合，从汽车实际的爬坡过程出发，构建可靠度功能函数．在一级安全等级下，计算出不同设计速度下满足可靠度要求的爬坡车道长度，从而提供阶梯坡度范围内爬坡车道长度的限制要求．

1 主导车型的选择

随着公路里程的增加以及汽车产业结构的调整，大中型载重客货车、集装箱的比重在迅速增加．文献[7]通过对浙江省高速公路载重货车功率质量比进行调研，并结合载重货车车型比例，得出设计主导车型应为六轴汽车列车，功率质量比为7.04～8.43 kW/t．文献[8]基于对济青高速公路济南收费站的车辆统计数据分析，并在西铜高速进行实地观测，拟定纵坡设计主导车型功率质量比为7.45～8.50 kW/t．综合以上考虑，结合未来货车载重越来越大的发展趋势,拟定功率质量比7.58 kW/t，一汽解放J7牵引车CA4250P77K25 T1E5为主导车型，车辆相关计算参数见表1．

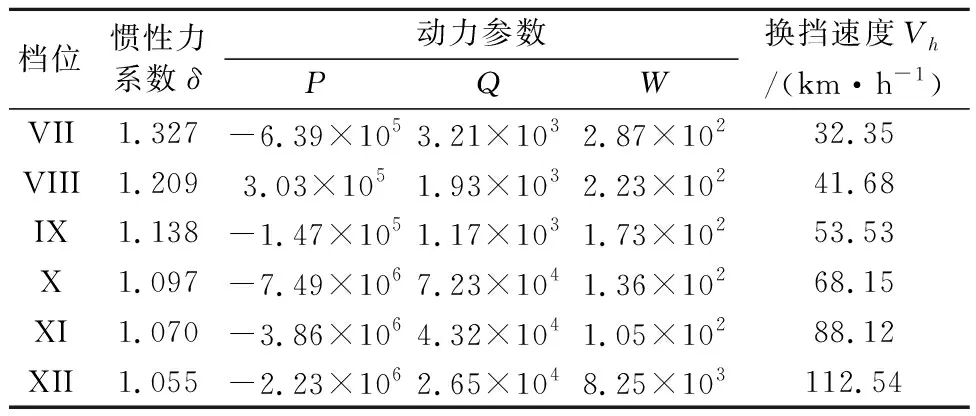
表1 代表车型计算参数表

2 爬坡车道的设置及长度的确定

2.1 爬坡车道的设置

文献[9]表明小于3%的纵坡坡度对大型车上坡行驶的速度影响很小，大于3%的纵坡坡度对大型车上坡行驶的速度影响较大．而JTG D20-2017《公路路线设计规范》 (以下简称《规范》)中表明，六车道以上的高速公路可不设爬坡车道．因此本研究仅对设计速度为100、80 km/h，坡度在3%以上的路段进行爬坡车道设计，规范中典型爬坡车道(假设陡坡相邻路段皆为缓坡)布置图见图1．

图1 典型爬坡车道布置图

由图1可知：爬坡车道长度由爬坡段和附加长度两部分组成，同时在起终点分别设立分流渐变段和汇流渐变段；文献[10-16]通过VISSIM仿真实验，分析货车在爬坡路行驶时的速度折减量，从行车安全的角度提出以20 km/h速度折减量作为设置爬坡车道起点的依据；基于此，文中将车辆速度折减20 km/h的位置作为爬坡车道起点，将坡底至爬坡车道起点的距离作为车辆的减速行程S1；起点至坡顶的距离作为爬坡段，在坡度坡长已知的条件下，爬坡段的长度即为坡长S减去车辆的减速行程S1，即为S-S1．其中，不同纵坡对应最大坡长值见表2．附加长度S2的确定则参考规范中的说明，列于表3．

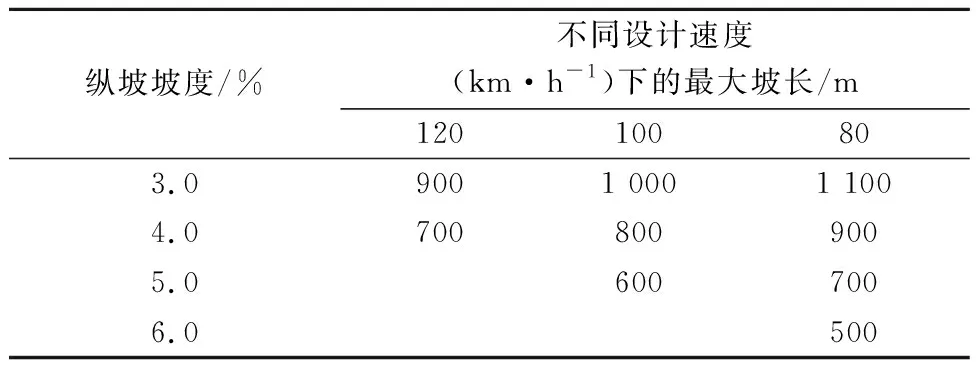
表2 不同纵坡最大坡长

表3 陡坡路段延伸后的附加长度

2.2 爬坡车道长度的确定

汽车上坡过程中的所受阻力是复杂的，文中参考文献[11]的研究成果，综合考虑汽车在爬坡过程中的运动状态及汽车进行加减档的带来的影响，得到以下计算模型：

(1)

式中：λ为修正系数，取为1；g为重力加速度，g=9.8 m/s2;V1为汽车在爬坡路段坡底的运行速度，km/h；f为滚动轮胎的阻力系数,高速公路取值为0.01；i为道路纵坡坡度，%．

综合前文所述，爬坡车道长度为

L1=S-S1+S2

(2)

式中：L1为汽车安全行驶所需的爬坡车道长度，m；S2为附加长度值，考虑到最不利情形，本研究陡坡路段延伸后的附加长度取为350 m.

由式(2)可知：当S

3 基于可靠度理论的爬坡车道长度分析

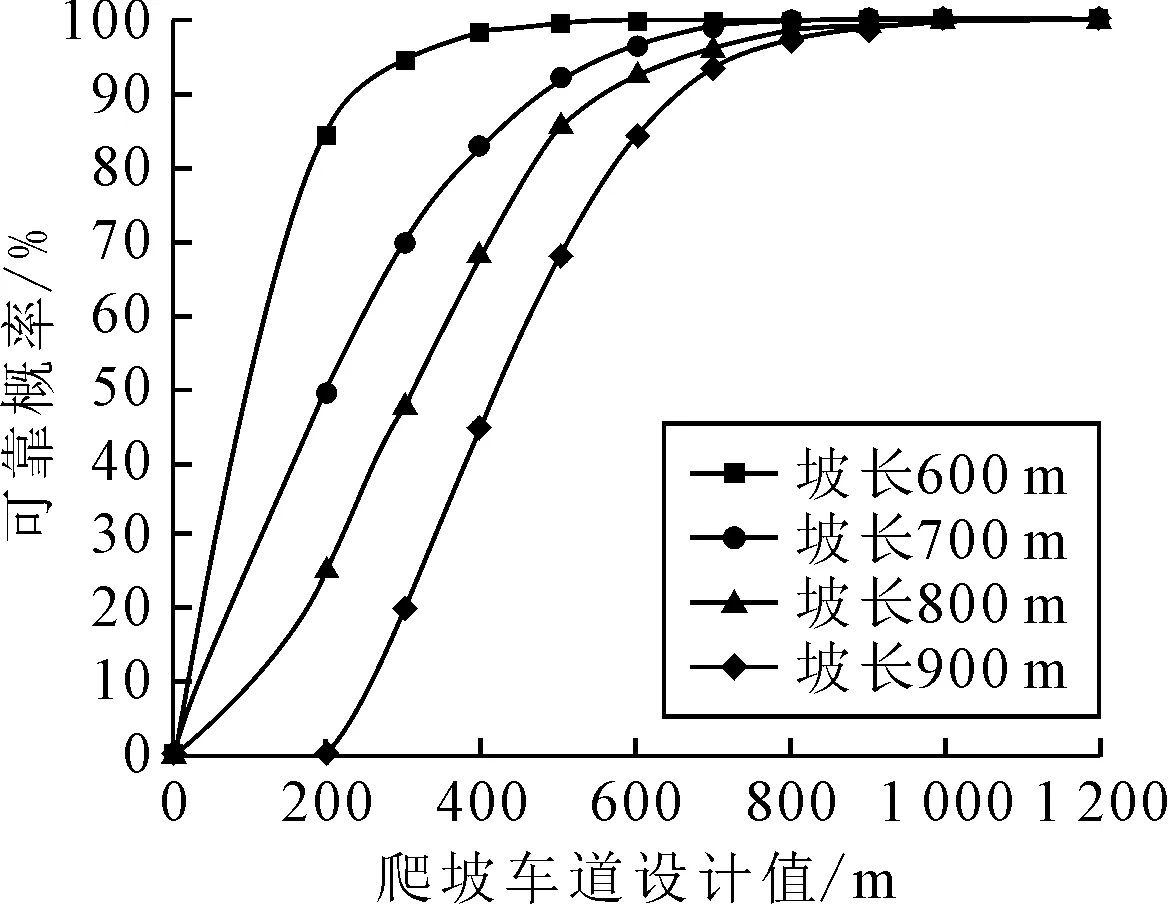
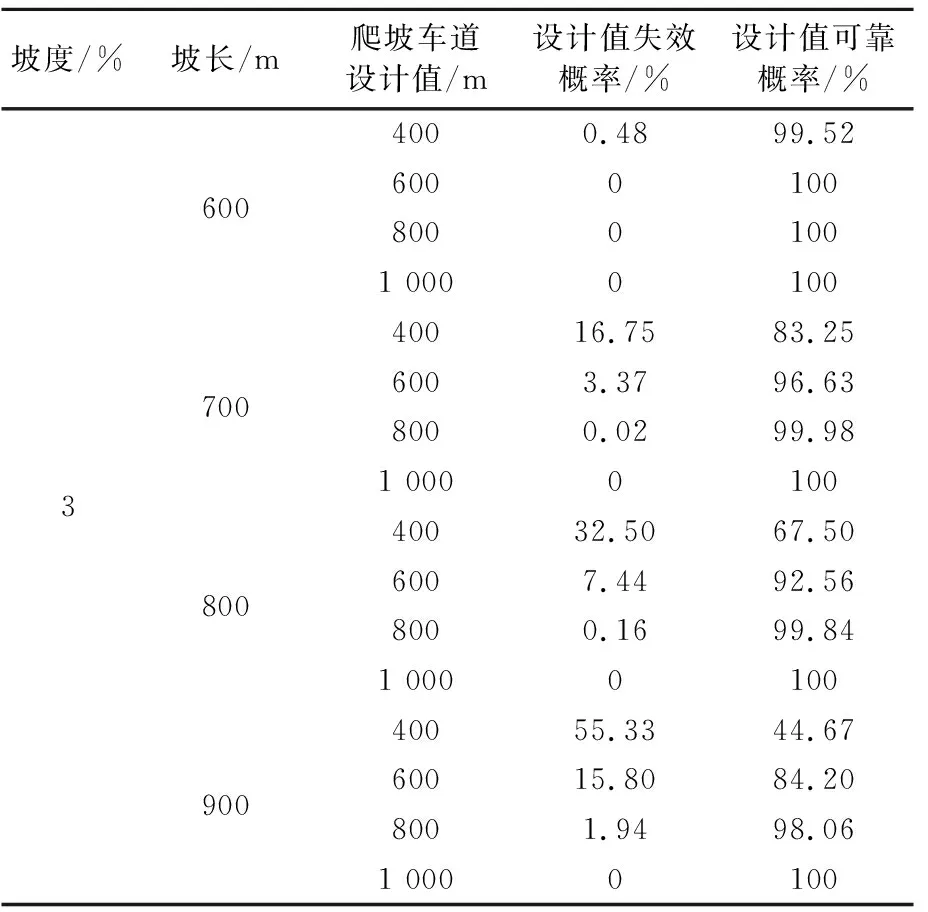
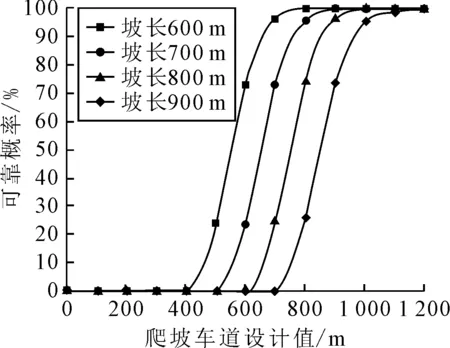
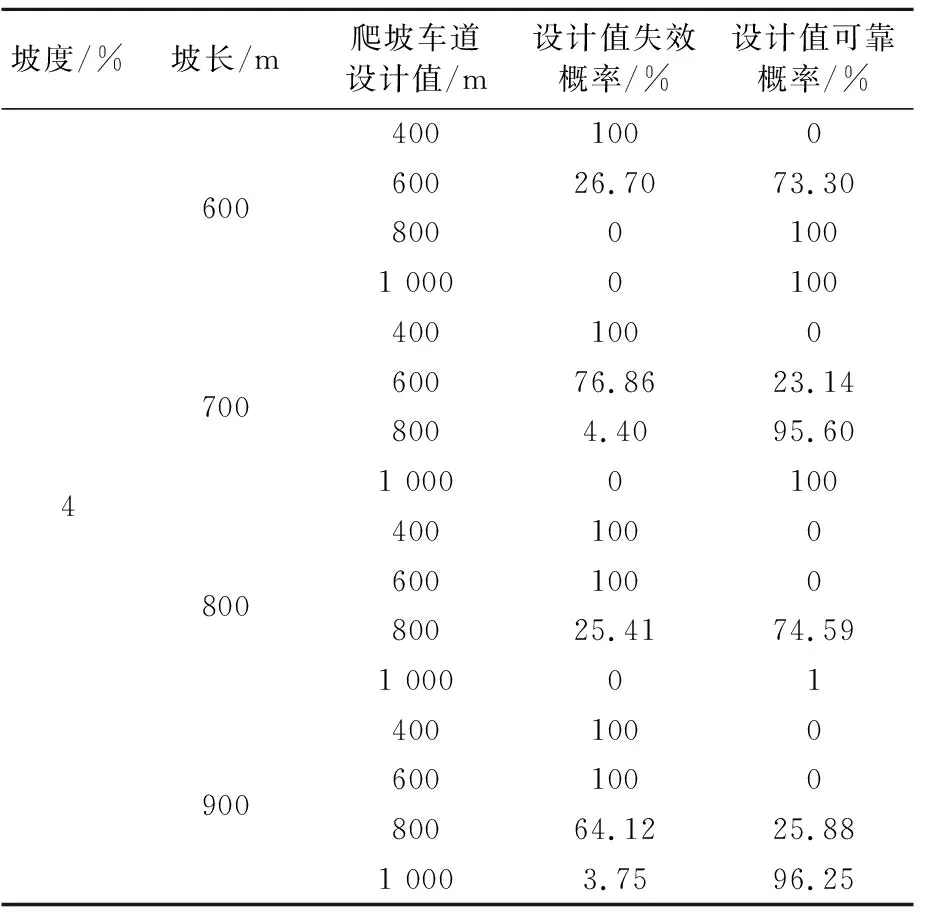
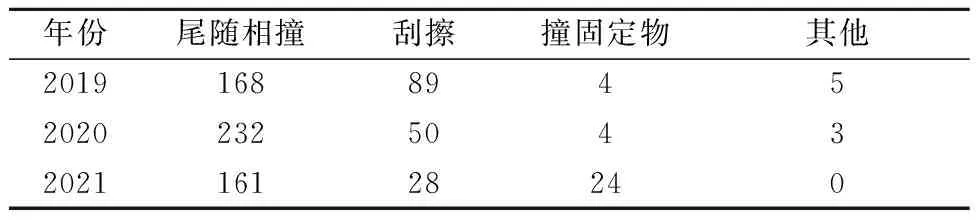
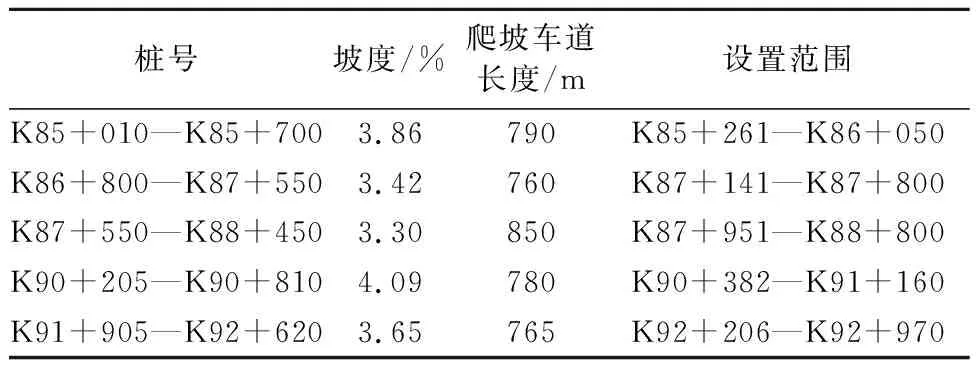
3.1 爬坡车道长度可靠度功能函数建立

文中将可靠度理论[12]引入爬坡车道设计中，用可靠概率、失效概率来评价爬坡车道设计中对于不同坡度坡长组合爬坡车道长度的可靠程度．车辆在上坡路段保证安全行驶所需要的爬坡车道长度值称为安全值;道路设计中所提供的行车长度值称为爬坡车道设计长度值，当设计值大于安全值便认为设计是可靠的，反之则设计值失效存在安全隐患．因此，依据前文所述，可将道路纵坡坡长可靠性的功能函数设为

Z=L-L1

(3)

式中：Z为爬坡车道长度可靠性功能函数；L1可由式(1)～式(2)计算得到；L为爬坡车道设计长度值．

3.2 可靠度功能函数参数分析

爬坡车道的修建依托于爬坡路段坡长与坡度的组合设计，因此，结合式(1)～(2)，在坡长与坡度的确定的条件下，只需对大型车进入爬坡路段坡底的运行速度进行测量．通过专业的测速仪器MetroCount5600进行车型划分及速度测量，将所观测的大型车速度样本数据进行统计整理后，对异常数据进行剔除．利用统计分析软件SPSS对数据进行单样K-S检验，整理之后结果见表4．

表4 高速公路爬坡路段坡底入口处车辆运行速度K-S检验表

3.3 爬坡车道长度可靠度求解

式(2)阐述了爬坡车道长度值与设计坡长坡度间的计算关系，式中含有积分的表达式．因此，考虑到蒙特卡洛模拟法是以概率和统计理论方法为基础的一种计算方法，是使用随机数来解决计算问题的方法，可以用来求解含积分的爬坡车道长度功能函数可靠度．通过MATLAB软件编程，可以抽样模拟计算不同设计速度、不同设计坡度下，爬坡车道长度设计值的失效概率和可靠概率．蒙特卡洛模拟法计算爬坡车道长度可靠度的基本步骤如下.

步骤1定义抽样次数N=10 000，输入设计纵坡坡度i，设计坡长值S．

步骤2爬坡路段坡底速度V1由MATLAB根据表4中的已知分布随机产生，由式(2)并结合表1计算车辆在爬坡路段安全行驶所需的爬坡车道长度,即为安全值L1．

步骤3输入爬坡车道设计值L，记录满足L-L1>0的次数，并除以抽样次数100 000，计算可靠度．

在已知爬坡路段坡度和坡长的前提下，现以设计速度80 km/h、坡度为3%路段和坡度4%的路段为例，计算爬坡车道长度设计值的可靠概率；坡度为3%，可靠度计算结果见图2和表5．

图2 坡度为3%，爬坡车道设计值可靠度

表5 坡度为3%时爬坡车道长度设计值可靠度计算结果

坡度为4%，可靠度计算结果见图3和表6．

图3 坡度为4%，爬坡车道设计值可靠度

表6 坡度为4%时爬坡车道长度设计值可靠度计算结果

3.4 爬坡车道长度安全建议值

因为现有规范中对于道路设计中参数指标可靠度没有明确的规定，所以文中爬坡车道长度设计的可靠度要求参考《工程结构可靠性设计统一标准》中对路面结构目标可靠度的规定，见表7．

表7 不同安全等级对应的可靠度

基于此，仍以蒙特卡罗法计算在不同坡度坡长下，以满足高速公速95%可靠度为目标条件，计算爬坡车道长度，从而给出不同阶梯坡度坡长范围内，爬坡车道长度安全建议值，对结果四舍五入后列于表8～9．

由表8～9可知：对于代表车型，坡度越大，爬坡车道长度安全建议值越大；表明随着坡度的增大，车辆需要更大的坡长来抵消坡度对其性能的影响，这与前文的分析结果一致；同时，坡度越大，爬坡车道起点距坡底长度值越小，当坡度为3%时，需要在距坡底570 m左右的位置设置爬坡车道，而当坡度为5%时，则需要在距坡底145 m左右的位置设置爬坡车道，这表明了对于坡度越大的路段，需要更早的将大车分流到爬坡车道，以此来减少因大车减速过快而造成的一系列事故．

表8 设计速度80 km/h爬坡车道长度安全建议值

表9 设计速度100 km/h爬坡车道长度建议值

3.5 工程实例

现以高速公路G42宜昌至重庆段为例，设计速度为80 km/h，双向四车道．根据设计资料显示：该路段最大设计纵坡为4.09%，最大坡长为1 462 m,最短坡长为419 m，地面高程一般700～1 100 m，山体相对高差180～300 m，总体呈山多坡陡的地貌特征．“石门山色对斜晖，高岫馋馋耸翠微”正是描绘路线经过的水月寺镇的高岚胜景，但风景的秀丽掩盖不了设计中出现的问题．从相关部门调查的结果来看，此路段事故频发，其中连续纵坡路段K85-K92(爬坡车道布置范围为：K84+715-K88+000)事故率最高，表10详细列出了该路段2019—2021年春运时期各类事故分布及原因．

表10 事故原因分布表

由表10可知：车辆尾随相撞的比例最高，连续三年都超过了70%，这与文献[13]的研究成果是一致的．而根据前文所述，山区高速公路设置爬坡车道可有效解决大型车辆因速度下降过快而造成与小型车尾随相撞的状况．此路段虽已设置爬坡车道，但近10年来由于车辆大型化和交通量逐渐增大，可以看出原有的爬坡车道设计对改善交通安全的作用正在逐渐减小，原有爬坡车道的布置范围可靠程度有待商榷，基于此，计算原有爬坡车道长度的可靠度，列于表11．

表11 原有爬坡车道长度可靠度计算表

由表11可知：按原有爬坡车道布置时，有三处路段可靠度计算结果低于安全等级一级对应的95%可靠度，而结合前文所述，此路段事故频发，因此需要重新对该路段进行爬坡车道长度设计．基于此，选取路段K84-K92中坡度大于3%的路段进行爬坡车道长度设计，仍采用蒙特卡罗法，对单个路段进行10 000次抽样，计算满足一级安全等级95%可靠度所对应的爬坡车道长度，并将计算结果整理，列于表12．

由表12可知：共有五处路段设置了爬坡车道，总长度为3 945 m．虽然相比于原有的爬坡车道长度(3 285 m)只增加了660 m，但表中的爬坡车道布置针对于大于3%的路段，主要对陡坡路段进行设计，并未对缓坡路段进行考虑；而在公路纵坡设计中，缓坡对道路线性安全的影响较小，因此表12的长度布置对于山区高速公路爬坡车道设计更有针对性，按照表中的设置范围进行爬坡车道设计可有效提高道路安全性，具有一定的工程意义．

表12 爬坡车道长度布置表

4 结 论

1) 根据汽车实际的爬坡过程，以20 km/h速度折减量作为设置爬坡车道起点的依据，建立爬坡车道长度与坡度的计算模型，利用蒙特卡洛法计算在不同坡度坡长条件下，爬坡车道长度设计值的可靠概率，并根据安全等级一级95%的可靠度要求计算出不同坡度下的爬坡车道安全建议值；当设计速度为80 km/h时，坡长为700 m的条件下，坡度为3%时对应的安全建议值为580 m，坡度为4%时对应的安全建议值为800 m，对应最大纵坡5%的安全建议值为895 m；当设计速度为100 km/h时，坡长为700 m的条件下，坡度为3%时无需设置爬坡车道，对应最大坡度为4%时的安全建议值为770 m．

2) 现有规范中没有对爬坡车道长度设计的可靠度作出明确规定，本研究以《工程结构可靠性设计统一标准》为依托求解可靠度函数并结合相关实例，从而提供了阶梯坡度范围内爬坡车道长度的限制要求，但同时，爬坡车道长度设计的可靠度如何规定也是今后需要研究的问题．