一种半约束模适航仪动力特性分析

2022-07-11周佳宇欧勇鹏

武汉理工大学学报（交通科学与工程版） 2022年3期

许勇周佳宇欧勇鹏

(海装广州局驻湛江地区军事代表室1) 湛江 524000) (海军工程大学舰船工程学院2) 武汉 430033)

0 引言

在船舶流体力学研究领域，船模耐波性试验是考核理论计算方法和阐述船舶流体力学机理的关键[1]，通过模型耐波性试验可获得船模部分运动模态的频率响应函数，据此可预报实船在给定浪级下的运动统计值[2].适航仪是开展船模耐波性试验所需的重要装置，传统的适航仪结构简单，能够测量船模的纵向运动，但不能测量船模横摇运动.由于横摇水动力的复杂性，特别是两船近距离航行时，因船间水动力干扰作用，使得横摇运动特性更为复杂，目前的理论计算尚未达到纵向预报的精度，需借助模型试验获得.与单船模耐波性试验相比，两船模的运动测试分析技术要更复杂：①需设置两套适航仪对模型进行拖曳，但常规的拖曳水池拖车按照单船设计，当加装另一套适航仪时，可能影响拖车运行性能；②要测量有航速情况下两船模间水动力干扰对横摇的影响，适航仪要能释放船模的横摇运动，且要约束船模的横荡及首摇运动，防止两船模在航行时相碰；③所用的适航仪应尽量减少对船模自由模态运动的影响.文献[3]开展了两船模并行航行时运动响应的测量试验，船模横荡及纵荡方向上加装了弹簧，防止船模相碰，但这限制了船模的横摇运动.Ronaess[4]在MARINTEK水池开展了波浪中一大一小两模型并行航行时运动响应测量试验，其适航仪主要结构为两摇臂装置，可以释放两船的横摇、垂荡、纵摇及部分纵荡运动，但因测量装置原因，小船的横摇运动测量值明显偏小[5].挪威MARINTEK拖曳水池设计了两模型并行航行时耐波性测量试验装置[6]，每一船模的适航仪由前后两摇臂装置构成，能够释放船模的横摇、纵摇、垂荡运动.海军工程大学自主设计了以摇臂装置为主要组成的半约束模适航仪，并开展了两船模近距离并行航行时运动响应测量试验，该适航仪能够释放船模的垂荡、纵摇及部分纵荡运动[7].综上可见，国内外研究机构多借助摇臂装置来实现船模的多自由度运动，特别是横摇运动的释放.该装置的特点是结构相对简单，且采用平衡锤对装置自重进行平衡，保证了装置的静态平衡.

在摇臂装置的牵引下，船模在拖曳水池中航行，遭遇波浪后作多自由度的摇荡运动，其运动为多个模态的耦合运动，这种运动已不再是定常运动.而摇臂装置也随船模摆动，因此其运动也是非定常的，这种非定常运动产生的原因必然是船模对其作用的结果，相应地，其反作用也必然施加于船模上，若这种反作用力与船模受到的波浪力相比不可忽略时，将影响船模的实际运动，影响测量数据的可靠性.如何计算这种作用力并评估其对船模运动响应的影响，目前还尚未有文献发表.文中以文献[7]所用半约束模适航仪为研究对象，对其进行了运动及受力分析，采用刚体动力学理论建立了摇臂装置的运动学及动力学计算模型，以一组船模运动仿真数据为输入进行仿真分析，验证了数学模型的可靠性.同时以实测船模运动数据为输入，分析摇臂装置的动力特性，并对实测数据进行评估.

1 试验原理及方程

1.1 半约束模适航仪工作组成及原理

半约束模适航仪由两套同型摇臂装置及导航杆组成，其结构及安装见图1.两摇臂装置一前一后安装在船模纵剖面上，每一摇臂装置包括水平摇臂和竖直摇臂，摇臂中心线均在船模纵剖面内.水平摇臂通过滚动轴承悬挂于拖车支架下，竖直摇臂通过连接轴承与水平摇臂一端相连，两摇臂只能在纵剖面方向内运动.在两摇臂的非连接端设置平衡锤，在静态时保证竖直摇臂绕两摇臂连接轴承中心无力偶作用，水平摇臂连同竖直摇臂绕拖车支架处轴承中心无力偶作用.两竖直摇臂下端通过万向节与安装在船模底板上的两横摇装置相连，两横摇装置在同一水平面内，且中心连线通过船模重心，船模可绕横摇装置中心连线作横摇运动.导航杆沿垂向布置在船模纵剖面内，上端固连在拖车上，下端安装一滑轮，通过钢丝绳牵引船模沿拖车前进方向运动.摇臂装置在静态时因平衡锤的作用能够保持随遇平衡状态，不会给船模施加作用力，当船模在波浪中作摇荡运动时，和船模连接的摇摆装置也会随船摇摆，在随船坐标系下，垂直摇臂作既有平移又有转动的平面运动，水平摇臂则作定轴转动.

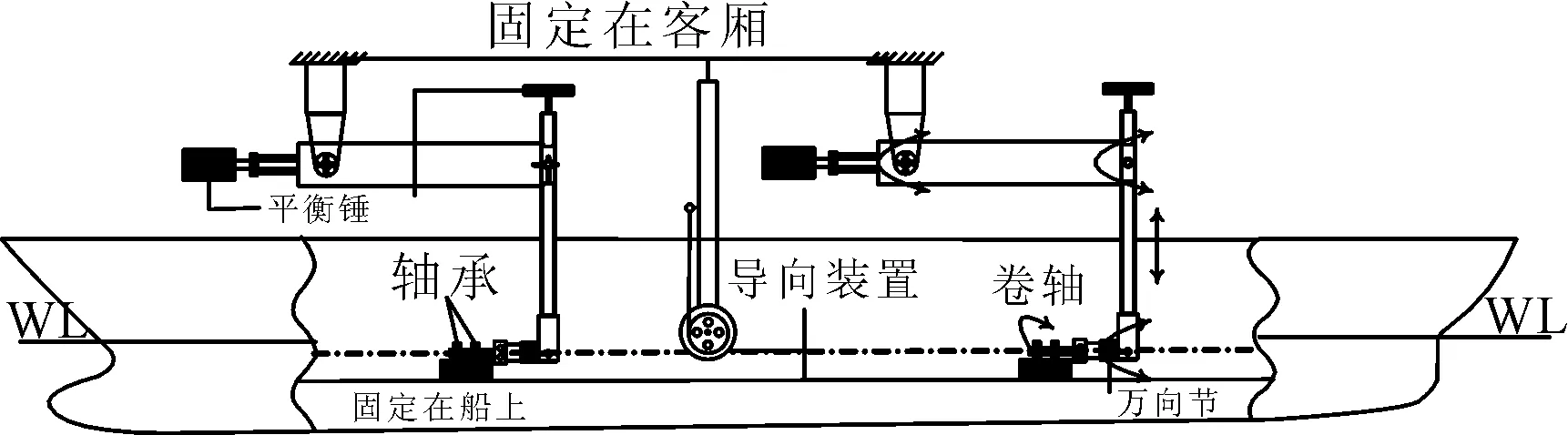
图1 半约束模适航仪结构及安装

1.2 坐标系

以靠近船首的摇臂装置作为研究对象，建立图2的直角随船坐标系Gxz，该坐标系以拖车速度平移，其原点在船模的重心G处，Gx轴指向船首，Gz轴铅直向上为正.设摇臂装置和船体相连处为A，两摇臂相连接处为B，水平摇臂和拖车连接处为C，因采用滚动轴承进行连接，忽略连接处摩擦力的作用，因此静态时连接处本身无力偶作用.

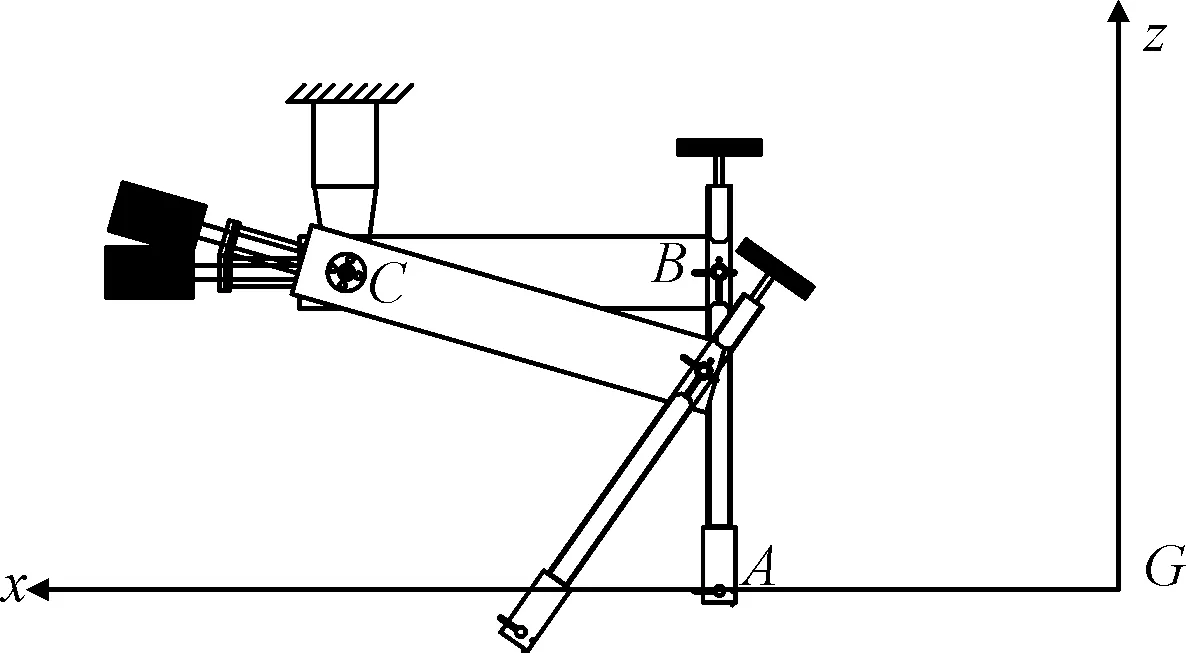
图2 坐标系及两摇臂运动分析

1.3 装置运动方程

设t时刻船模重心G的纵荡、垂荡、纵摇运动瞬时值分别为x(t)、z(t)、φ(t)，设xA(t)及zA(t)为A点在x及z方向的瞬时坐标，rGA为船体上A点到重心G处的距离，则船模上A点的运动为

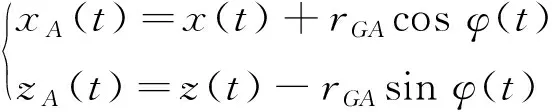
(1)

水平摇臂绕C作定轴转动，则B点绕C点在以rBC为半径的圆弧上运动，设水平摇臂在t时刻旋转的角度为θ(t)，当t=0时该角度为零，且水平摇臂处在水平位置，B点的瞬时坐标为

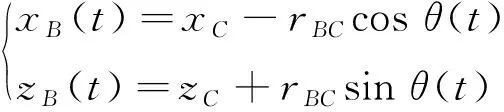
(2)

式中：(xC,zC)为C点的坐标，由于该点固结在拖车上，因此在随船坐标系中该点的坐标为常值.注意到A，B两点同在竖直摇臂上，若设两点的距离为rAB，则A，B两点的瞬时坐标满足

(3)

将式(1)～(2)代入式(3)求解出θ(t).该角度实质上确定了水平摇臂的定轴转动，对其两次微分可求得水平摇臂的角加速度.将所求的θ(t)代入式(2)可求得B点的运动.根据静态时的平衡关系可知B点实质对应的是垂直摇臂的质心，因此确定了B点的运动就获得了垂直摇臂质心处的平动运动.利用A、B两点的运动还可确定垂直摇臂的旋转运动，设垂直摇臂在t时刻绕质心B旋转的角度为β(t)，初始时刻时θ(t)=0且垂直摇臂处于铅直状态，则该角度可通过式(4)求得，对β(t)求两次微分可求得垂直摇臂的角加速度.

(4)

1.4 装置动力方程

以垂直摇臂为研究对象，设其质量为mAB，绕质心B处的转动惯量为JAB，受力分析见图3.

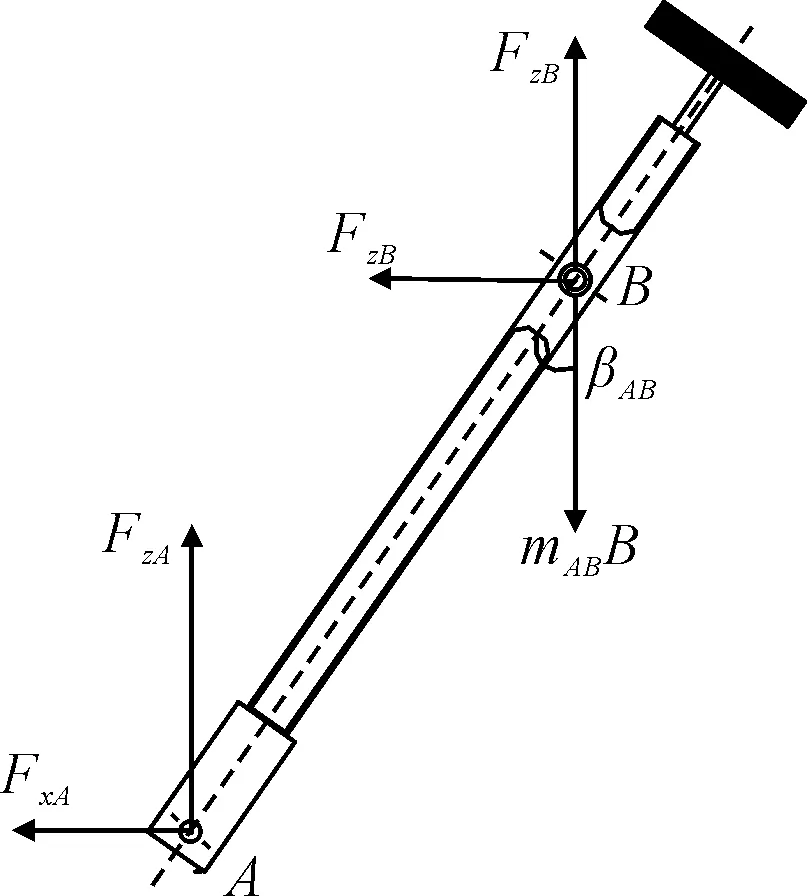
FxA，FzA-船模给垂直摇臂施加的x方向及z方向的作用力；FxB，FzB-水平摇臂给垂直摇臂施加的x方向及z方向的作用力；g-重力加速度.图3 竖直摇臂受力分析

根据刚体动力学理论，则垂直摇臂在平面内的运动微分方程为

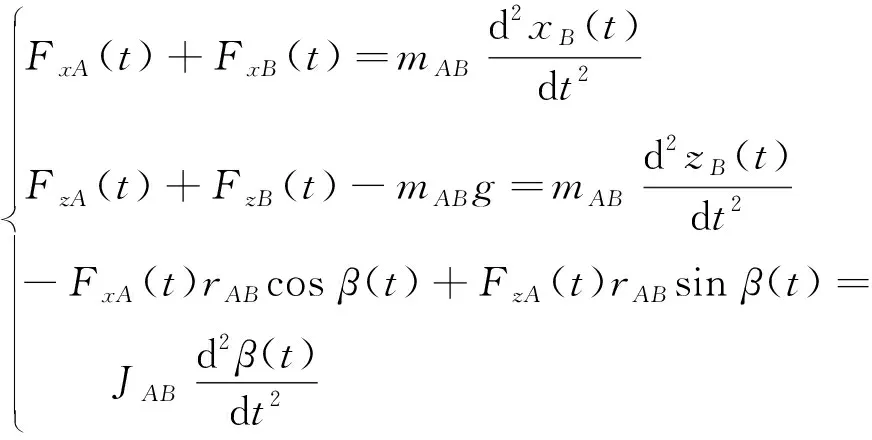
(5)

上述方程组有四个未知数，需补充一个方程才能求解.注意到水平摇臂绕点C作定轴转动，则可列出如下定轴转动微分方程

装配式住宅工程施工完成以后，施工单位首先要对质量进行检查，确保施工工程没有隐患风险，减少不必要的麻烦，同时还要做好最基本的防护工作。监理人员要根据工程情况来设计防护方案，确保每项工程的质量都能达到标准，比如装配式住宅工程关键部位的连接情况和住宅的沉降量等，保证在既定设计范围内，避免出现裂缝问题，从而影响到住宅工程使用。

FxB(t)rBCsinθ(t)-FzB(t)cosθ(t)+

(6)

式中：mBC及JBC为水平摇臂的质量及绕C点的转动惯量；rCD为水平摇臂(连同其平衡锤)重心距C点的距离；rCD=mABrBC/rCD.联立式(5)和(6)可解出A，B两点处的受力，摇臂装置对船模的作用力即为A点的反作用力.同理可求得靠近船尾处摇臂装置对船体施加的作用力，将这两个力简化到船体重心则可求得适航仪施加于船模上的纵向作用力FGx、垂向作用力FGz及在GXZ平面内的作用力矩MG.

2 实例分析

文献[7]利用图1的适航仪在武汉理工大学长条形拖曳水池开展了规则波中两半约束模(分别记作船模a、船模b)顶浪航行时运动响应测量试验.摇臂为铝质结构(密度约为2 700 kg/m3)，平衡锤为铸铁材质.水平摇臂连同其平衡锤质量7 kg，相对C点转动惯量0.229 kgm2，B、C两点距离0.5 m，垂直摇臂连同其平衡锤质量1.5 kg，绕B点转动惯量0.076 kgm2，A、B两点距离0.55 m.靠近船首的摇臂与船模连接点距离船模重心的距离为0.9 m，靠船尾的摇臂与船模连接点距离船模重心的距离为0.88 m.船模a重173 kg，水线长3.651 m、宽0.462 m，设计吃水0.156 m，船b重226 kg，水线长4.352 m、宽0.524 m，设计吃水0.148m，模型其他主要参数及三维轮廓参见文献[7].两船模中对中布置，横向间距(两船模重心在横向的距离)为0.35La(La为船模a的水线长)，两船模航速对应的弗劳德数Fr为0.171.规则入射波波长λ范围为2～10 m，波高ξ0为70 mm.图4为两半约束模并行航行时拍摄的试验相片.针对该试验及适航仪，采用上述算法编制了摇臂装置运动及受力计算程序.程序界面见图5，该程序可利用实测船模的纵荡、垂荡及纵摇运动过程，模拟和计算两摇臂装置的实时运动及摇臂装置摇摆运动过程中对船模的作用力(力矩).

图4 两半约束模在规则波中顶浪航行

图5 摇臂装置运动模拟及附加力计算程序

2.1 数值处理方法

在数值求解方程(3)时会求得两个根，对应两个B点位置，需对其进行判定，舍去不合理的根.对式(3)进一步化简为

zAC(t)sinθ(t)]=0

(7)

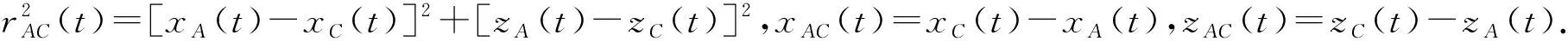
cos[θ(t0)+θ0]=C

(8)

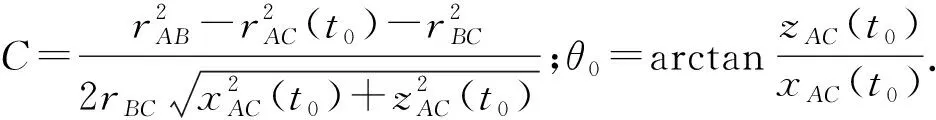
根据水平摇臂作定轴运动的范围可知-90°<θ(t)<90°，而由余弦函数的性质可知在[-90°,90°]内方程(8)仅有一个根，因此在数值计算时仅需加入-90°<θ(t)<90°的判别条件就能舍去不满足条件的根.

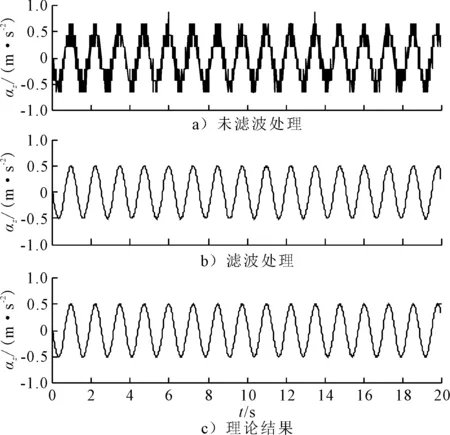
图6 前摇臂装置垂直摇臂A点处垂加速度

由图6可知:直接微分运算确实存在较大数值误差，而采用CEEMD方法处理后所得结果和理论值吻合良好.对图6a)及图6b)曲线的平均幅值和平均周期进行了统计，未滤波处理时所得平均幅值为0.429 m/s2，平均周期为0.423 rad/s，与理论值(幅值0.5 m/s2，平均周期为1.256 rad/s)相比存在较大误差，势必影响摇臂装置作用力(力矩)的计算精度，进行滤波处理时所得平均幅值及平均周期分别为0.501 m/s2、1.256 rad/s，与理论值相当接近.因此，对微分结果进行滤波处理是必要的，同时，上述结果也说明本文建立的数值计算模型是可靠的，能够用于实测数据的计算与分析.

2.2 摇臂运动及受力计算

图7为两约束模在工况λ/La=0.82时模型a测量得到的纵荡、垂荡及纵摇时历曲线，以此为输入，采用本文方法对船模a两摇臂的运动及摇臂装置对船模的附加作用力(力矩)进行计算.图8为靠近船首的垂直摇臂质心处的加速度及角加速度时历过程，该工况下求得的前后两套摇臂机构对船体附加的作用力及力矩见图9.

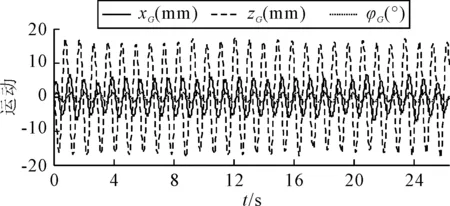
图7 半约束模a的纵荡、垂荡及纵摇时历曲线

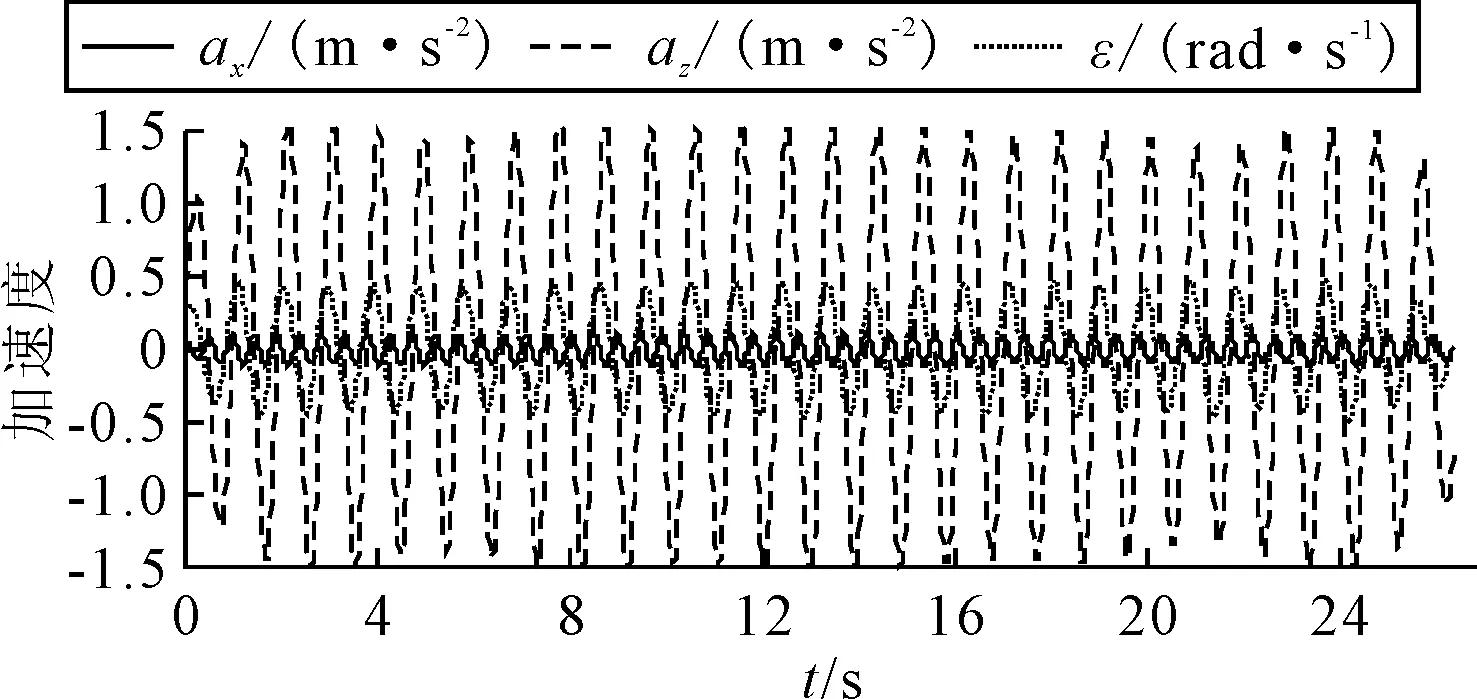
图8 前摇臂装置垂直摇臂质心处的加速度及摇臂角加速度

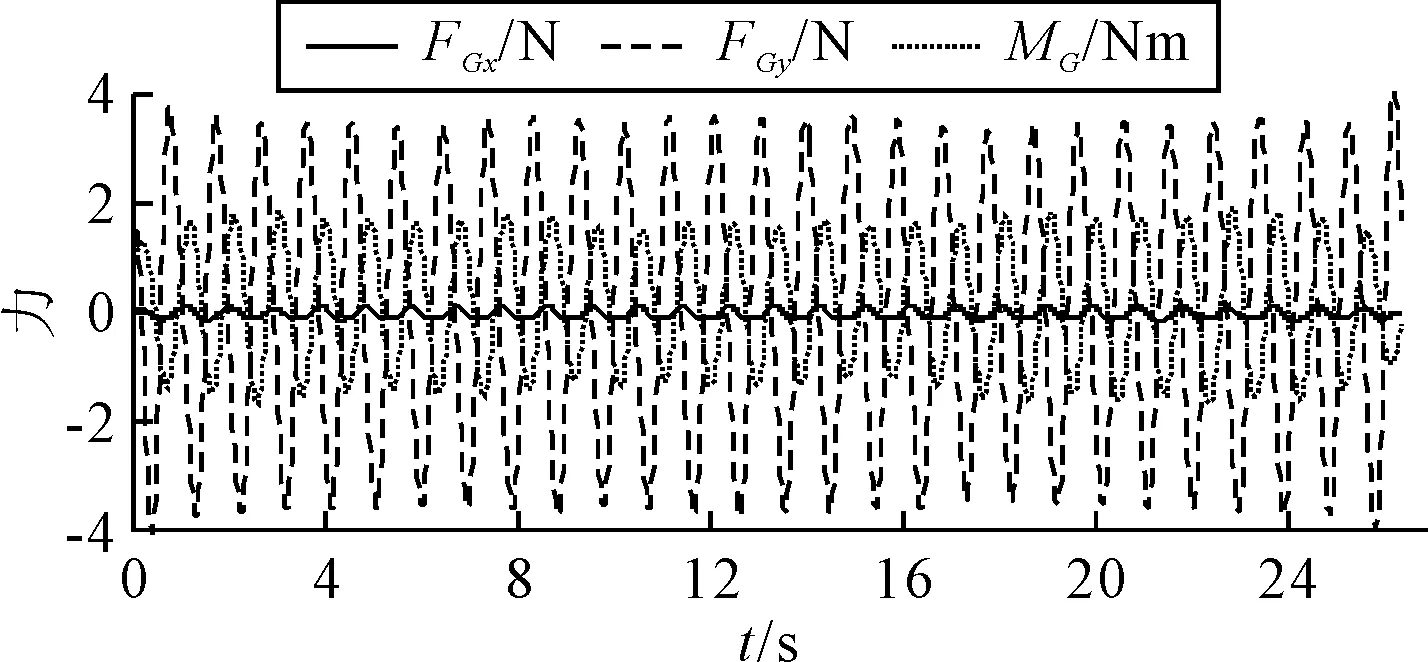
图9 两摇臂机构对船体的附加力及力矩

由图8～9可知:垂直摇臂机构的加速度及角加速度时历曲线仍以一阶运动(以遭遇频率作简谐振动时的加速度或角速度)为主，而附加作用力同样以一阶为主.

2.3 摇臂装置对船模作用力评估

采用同样方法对其他入射波长的情况进行了计算，统计了遭遇频率处摇臂装置施加于船模的作用力及力矩的幅值.为便于比较，在航速、入射波参数、船模相对位置等试验条件相同的工况下，对船a全约束，船b半约束时船a所受波浪力进行了测量，测量方法及试验情况详见文献[7].图10为纵向的附加力与约束模试验测量的纵荡力幅值的比值随波长船长比的变化曲线，图11为垂向附加力与实测垂荡波浪力幅值的比值随波长船长比的变化曲线，图12为附加纵摇力矩与纵摇波浪力矩的比值.另外，图中还给出了当摇臂装置采用钢制结构时(摇臂尺寸形状不变)，船模所受摇臂装置附加力(或力矩)的计算结果.

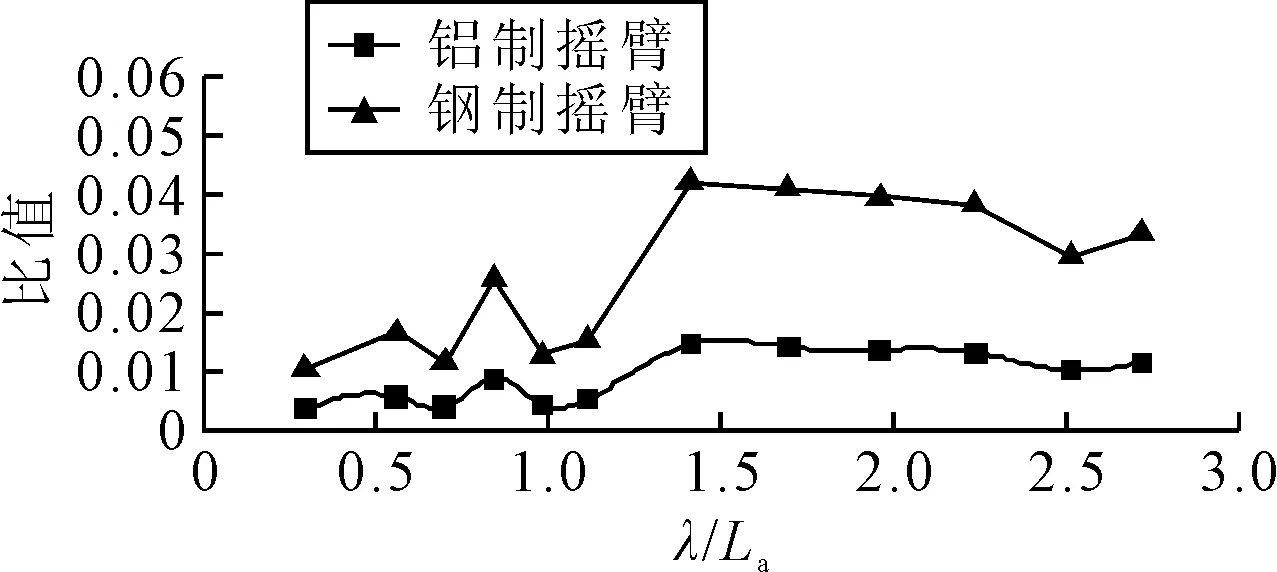
图10 遭遇频率处纵向附加力与船体纵荡力比值

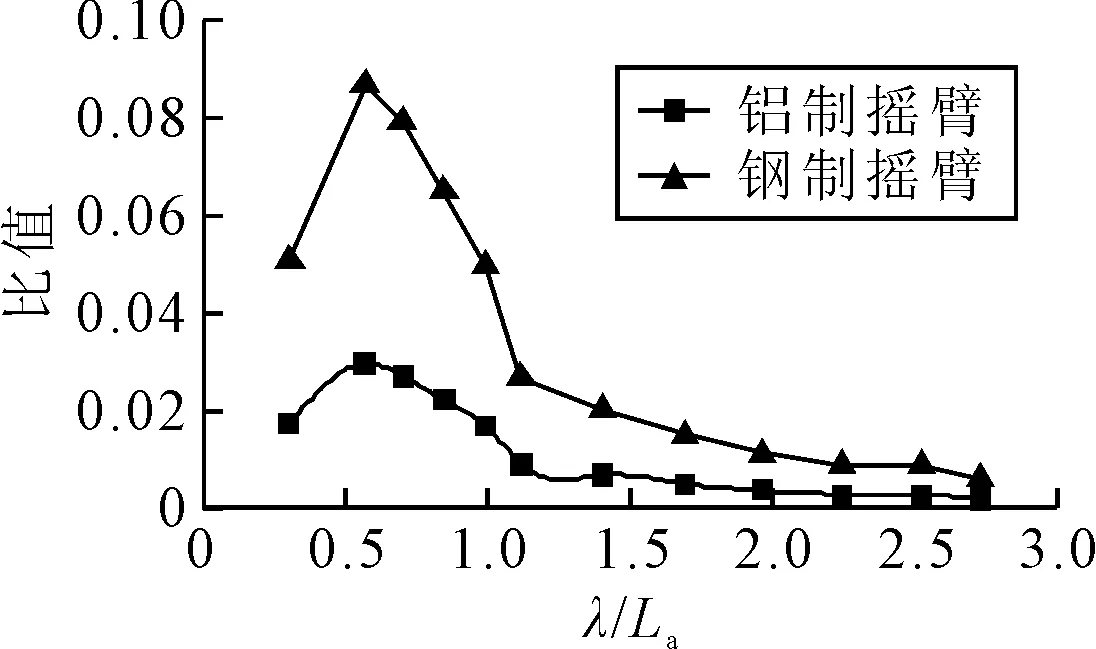
图11 遭遇频率处纵向附加力与船体纵荡力比值

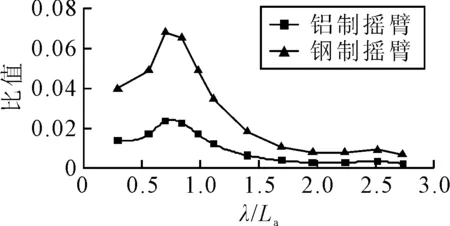
图12 遭遇频率处附加力矩与船体波浪纵摇力矩比值

由图10～12可知：①平衡锤虽然能保证摇臂装置在静态处于平衡状态，但当摇臂装置随着船模作摇摆运动时，其对船模确实有附加力(力矩)作用；②铝制摇臂及钢制摇臂对船模的附加力(或力矩)随波长船长比的变化规律一致，纵向附加力与纵荡力的比值随波长船长比的增加有增大趋势，其原因在于在长波中船模具有较大幅度的纵荡运动引起的，垂向附加力及附加纵摇力矩在长波中的值很小，在共振频率附近其比值相对较大；③相同波长船长比工况下，钢制摇臂对船模产生的附加力(或力矩)远大于铝制摇臂对船模产生的附加力(或力矩)，两者比值约为2.9，刚好为钢和铝的密度比值，这说明摇臂装置对船模的附加力(或力矩)与摇臂装置的质量(或惯量)成正比，因此在保证装置强度的情况下减小装置的质量和惯量是减少摇臂对船模附加力(或力矩)的关键；④从比值的量值来看，铝制摇臂的纵向附加力比值小于2%，垂向力对应的比值小于3.5%，而附加力矩对应比值小于3%，这种附加力远远小于船模实际受到的波浪作用力，对船模的纵荡、垂荡及纵摇运动的影响可忽略.