分块瓦导轴承双向流固耦合动力特性数值模拟

王思淼，王文全，闫 妍，王 秀

(1.昆明理工大学 建筑工程学院，云南 昆明 650500；2.四川大学 水利水电学院，四川 成都 610065；3.四川大学 水力学与山区河流开发保护国家重点实验室，四川 成都 610065)

水力发电是可再生能源的重要组成部分，约占全球发电量的20%[1]。水力发电具有产电量大，产能稳定等优点，在能源供给中占据十分重要的位置。我国山川河流较多，水头落差大，水能资源丰富[2-3]，截至2020年底，我国常规水电装机达到3.38亿kW，年发电量1.35万亿kW·h，在建规模约4 800万kW；抽水蓄能装机3 149万kW，在建规模5 373万kW[4]。我国目前机电排灌保有量居世界第一，但仍有巨大的水力资源待开发利用[5-7]。

水力发电机组是水力发电站的核心动力机械设备，能够将水流冲击的能量转换为旋转机械能，通过主轴带动发电机转子转动产生电能。而水轮发电机组作为大型旋转机械，在运行中存在振动和摆动问题。水轮发电机组轴系的稳定性和振动特性是反映机组运行质量的重要指标，同时会影响到机组的安全运行和使用寿命[8]。过大的主轴振动会引起机组动静碰摩、加速零部件的磨损、造成构件疲劳损伤等故障，当机组的振动非常严重时，发电站轻则停机停产，重则毁坏机组，造成严重的破坏性事故，最终影响电网的安全运行[9]。所以，保证水轮发电机组安全稳定地运行是当前研究的重要课题。目前，水力发电电站大多是采用机组竖直安装的方式，即主轴系部分为铅垂方向安装，整个轴系包括主轴、安装在主轴上的转子、转轮等部件，工作状态下主轴所受到的外界载荷均由主轴上的导轴承承担[10]。水电站所使用的大部分机组均采用三导轴承布置，即只有上导、下导和水导3个导轴承，用来约束及承载整个轴系的工作载荷。导轴承则需要承担主轴上的全部径向载荷，导轴承的动力特性是关乎主轴轴系安全的关键因素之一[9,11-12]。所以，确保轴承拥有足够的承载能力和强度是导轴承研究的重要内容。

目前，国内外对导轴承的研究主要以轴瓦静力分析或单独分析油膜压力为主。杨晓明、马震岳等[13]采用有限元方法分析了立式可倾瓦导轴承的动力特性；张雷克等[14]讨论了密封间隙对轴系的影响；张金剑等[15]分析了质量偏心对轴系运动的影响。导轴承对主轴轴系的约束作用主要取决于导轴承的几何尺寸，而本文中采用双向流固耦合动力学计算方法，讨论轴瓦数、油膜间隙厚度和偏心距对轴瓦和轴颈应力分布的影响，得出较为贴近真实工况下的数值结果，为水轮发电机导轴承的优化设计提供有益的参考。

1 控制方程及数值模型建立

1.1 流固耦合控制方程

流固耦合分析方法用于解决流体与固体之间相互作用问题。水轮发电机导轴承内采用油膜润滑来约束主轴工作中的运动偏心，油膜、轴瓦与主轴之间的相互作用是典型的流固耦合问题。采用流固耦合分析方法可以贴近真实情况地模拟分析轴瓦和轴颈的实际应力和变形情况。

流体控制方程为质量守恒方程式(1)和动量守恒方程式(2)：

(1)

(2)

其中：t表示时间，ff是体积力矢量，ρf是流体密度，v是流体速度矢量，τf是剪切力张量，表示为

τf=(-p+μ▽·v)I+2μe

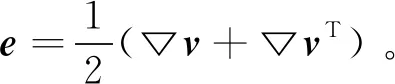
固体控制方程为

(3)

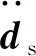
在流体与固体耦合的交界面上，流体与固体应力和位移相等，即

(4)

其中：f下标表示流体，s下标表示固体。

1.2 导轴承模型的建立

本次计算所建立的模型参考立式水轮发电机组(水轮机组HLA551-LJ-43，发电机SF55-10/740)，导轴承参数参考机组的上导轴承尺寸。为模拟主轴运转过程中发生偏心时轴瓦的受力情况，模型中轴系转动部分只取主轴部分长度，研究轴段全长取轴承高度的11倍长度，轴承位置设置于主轴所取轴段部分的中点处。

分块瓦油润滑导轴承三维模型结构和轴承瓦片布置结构见图1。

计算所用导轴承模型尺寸如下：轴瓦包角为40°，轴瓦瓦片厚度15 mm，支撑的楔板高度为4 mm，主轴与导轴承接触的轴颈部分直径100 mm，主轴直径90 mm，导轴承高度为80 mm。

导轴承润滑所使用的油膜材料参数设置：润滑油密度为960 kg/m3，动力粘度为0.048 Pa·s，不考虑温度变化。

为后续结果显示方便，这里对轴瓦进行编号，如图1(b)所示，以图示位置左边轴瓦编号为1，顺时针方向旋转编号，轴瓦编号依次为2、3、4、…，所有轴瓦沿圆周方向均匀分布安装，后文提到偏心方向均为沿半径指向1号瓦中心，图中表示瓦片均用“WA”字母表示。

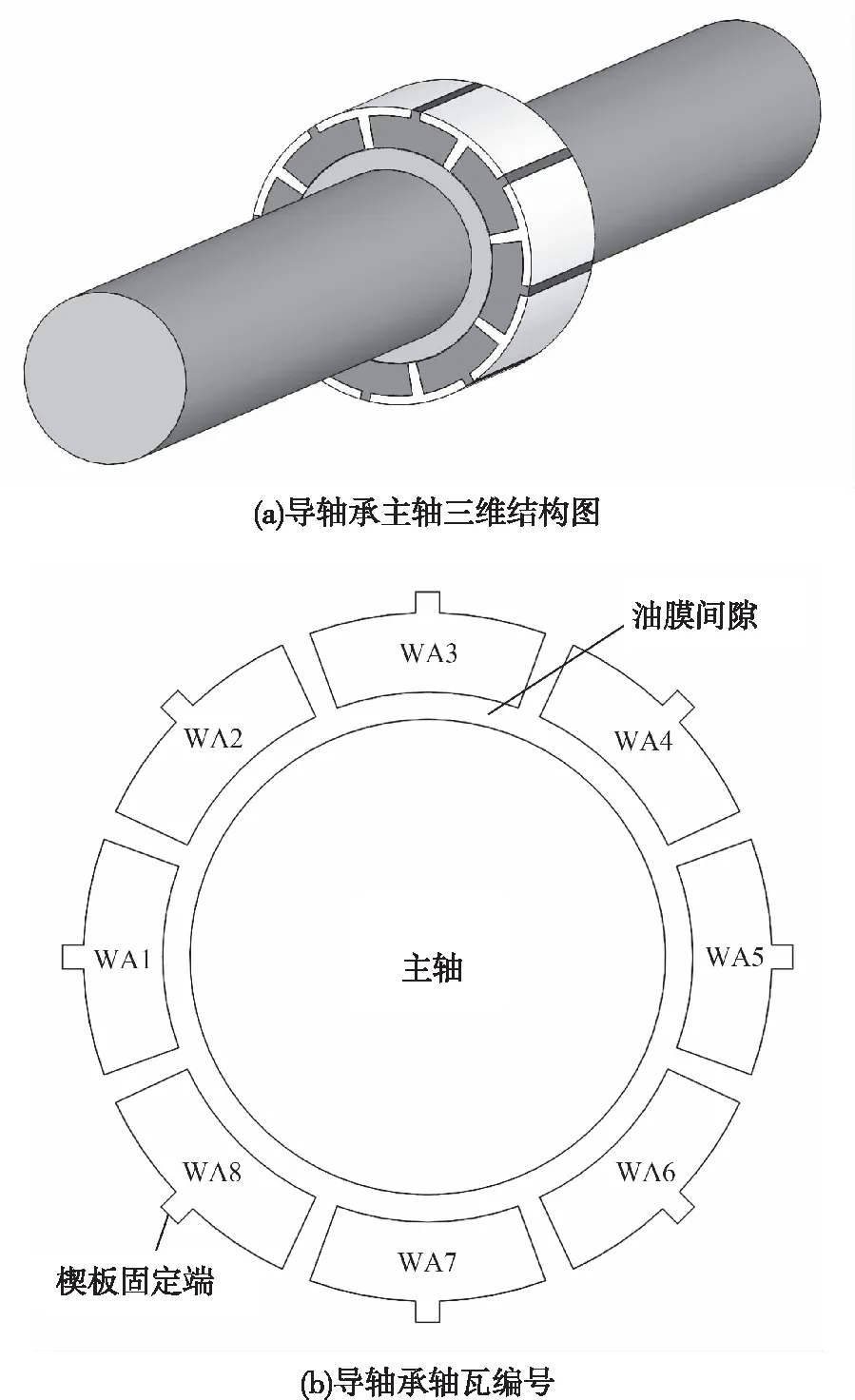
图1 轴承三维模型及轴瓦编号Fig.1 Bearing 3D model and bearing number

1.3 模型假设和边界条件

1)模型假设

根据实际模拟条件限制，对所分析的导轴承进行适当的模型简化假设。

(1)轴瓦楔板支撑位置假设为与楔板固结，即瓦片为固定瓦；

(2)油膜假设为牛顿液体，动力粘度沿油膜厚度方向稳定；

(3)油膜与主轴接触的壁面之间、油膜表面与主轴表面没有相对位移，不考虑由于摩擦而产生的热能。

2)边界条件

(1)支撑轴瓦的楔板固定端表面设置为混合固定边界，即该表面不存在变形与位移；

(2)油膜内表面设置为旋转边界，旋转速度与轴颈转速均为600 rpm；

(3)油膜除内表面外的其他表面设置为固定无滑移壁面；

(4)对偏心方式进行简化处理，偏心运动距离施加于研究轴段的上下两端面，模拟运转总时长设置为0.4 s，0～0.1 s主轴运转期间不发生偏心，0.1～0.2 s期间主轴轴线向1号轴瓦方向发生线性径向偏心，0.2～0.3 s期间主轴于设置的偏心距离位置运行，0.3～0.4 s期间主轴偏心线性回归与轴承同心位置。

3)模型网格数

网格划分采取分区域划分，油膜部分切分为圆环部分与轴瓦间油膜部分。圆环部分为主轴与轴瓦内面之间间隙区域。由于这部分几何尺寸很小，故单独划分网格，划分后网格单元数为378 840。固体部分网格单元数为635 026。模型总网格数为1 101 946。

1.4 计算模拟参数

改变导轴承3个主要参数进行模拟计算，分别是：瓦片数、油膜间隙厚度、不同主轴偏心距。对于瓦片数，选取5种瓦片数进行计算模拟(4块瓦片、5块瓦片、6块瓦片、7块瓦片、8块瓦片)；对于油膜间隙厚度，选取间隙分别为0.12、0.15、0.18 mm进行对比计算。根据瓦片数和油膜间隙的结果进行对比分析，最后选取油膜间隙0.15 mm，6块瓦片数的组合参数进行5种不同偏心距离的计算模拟。

2 结果与讨论

2.1 不同轴瓦数对导轴承动力特性的影响

模拟不同瓦块数时，油膜间隙取用0.12 mm。由于主轴发生偏心时，会对偏心方向的轴瓦产生最大压力，故只取最危险瓦片(即1号瓦片)结果为评断标准。图2为轴承瓦片数不同的情况下，主轴发生偏心时1号瓦片的应力大小。可以看出，主轴产生相同偏心距的情况下，轴承瓦片增加，可以使1号瓦片的最大应力值和平均应力值下降；当瓦片数从4增加到5、6、7、8时，相对于瓦片数为4的1号瓦片的应力峰值分别下降了4.71%、11.82%、20.96%、31.14%，应力均值分别下降了3.41%、8.78%、12.74%、19.16%。 应力峰值的显著下降可以使轴瓦在工作状态下更安全稳定。

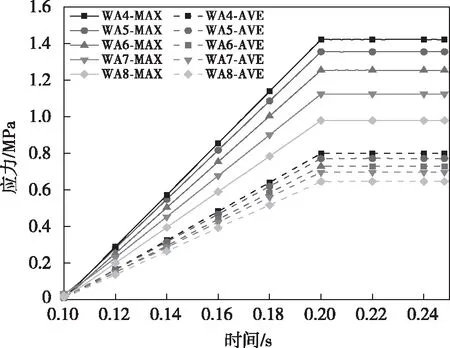
图2 不同瓦片数下瓦片最大应力值与平均应力值Fig.2 The maximum and average stress values of tiles under different number of tiles

图3是不同瓦片数情况下，1号瓦片受力发生位移的最大值和平均值。从图中可以看出，从5块瓦片增加到6块瓦片时，可以显著降低危险瓦片的最大位移值，但6块瓦片增加为7片时，形变量减小相对不明显；当瓦片数从4增加到5、6、7、8时，相对于瓦片数为4的1号瓦片的位移峰值分别下降了5.82%、19.17%、22.50%、33.50%，位移均值分别下降了12.33%、24.24%、29.26%、36.86%。

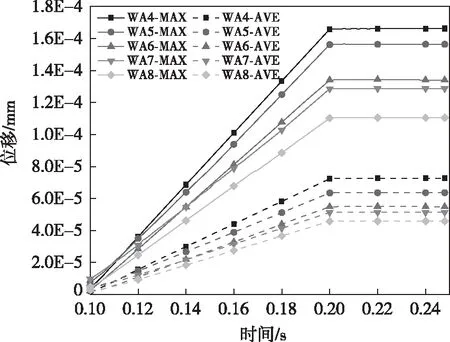
图3 不同瓦片数下瓦片最大形变值与平均形变值Fig.3 Maximum deformation value and average deformation value of tiles under different number of tiles

2.2 油膜间隙厚度对导轴承动力特性的影响

关于油膜间隙这一参数，对不同的瓦块数都进行3种油膜间隙(0.12、0.15、0.18 mm)的模拟分析。与上文2.1一样，1号瓦片受最大压力，为最危险瓦片，所以以1号瓦片峰值应力和轴瓦最大变形量作为参考标准进行分析，结果如表1所示。由表1和表2中结果可以看出：油膜间隙的变化对轴瓦所受应力和变形影响较小；但轴瓦数目变多，会使整体偏心产生的力分解为多个分力，减小单块瓦片所受的应力峰值，有利于防止轴瓦因应力过大发生破坏。

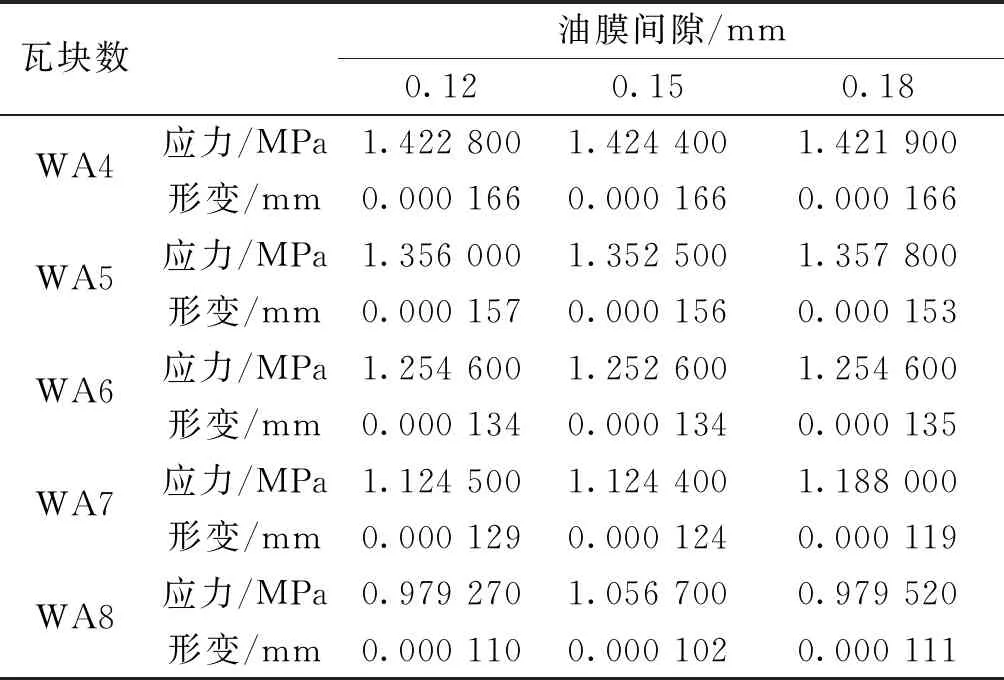
表1 不同油膜间隙下应力与形变量Tab.1 Stress and deformation under different oil film clearances

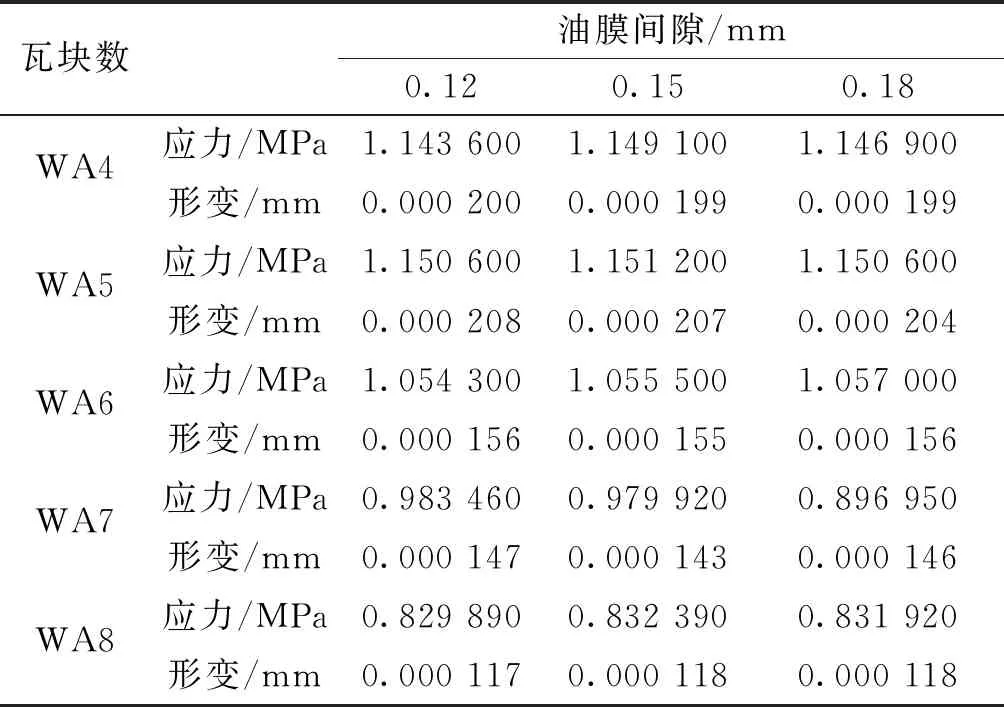
表2 不同油膜间隙下轴颈表面应力与形变量Tab.2 Surface stress and deformation of journal under different oil film clearances

2.3 主轴发生不同偏心距离对导轴承动力特性的影响

为探究不同偏心距离对轴瓦应力变形的影响，对油膜间隙0.15 mm、瓦块数为6的轴承模型，进行5个不同的偏心参数的模拟计算，偏心距离分别为0.01、0.02、0.03、0.04、0.05 mm。结果中提取6块瓦所受应力的最大值和平均值(图4)，形变的最大值和平均值(图5)。

由图4可以看出，偏心距离越大，对轴瓦的压力会变大，相对于偏心距0.01 mm的应力峰值2.016 8 MPa，当偏心距增加至0.02、0.03、0.04、0.05 mm时，应力峰值分别增加了97.28%、195.25%、294.11%、397.82%，应力峰值增加量随偏心距离的增加大致呈线性增长；偏心距为0.01 mm时应力均值为0.355 051 MPa，偏心距增加后应力均值增长量为100.67%、192.92%、302.07%、405.15%，同样呈线性增长。如图5，随着主轴偏心距离的增大，轴瓦的位移也随之增加，偏心距为0.01 mm时最大位移为0.000 134 mm，偏心距增加至0.02、0.03、0.04、0.05 mm时，相对于0.01 mm位移最大值分别增加98.36%、178.60%、295.84%、397.26%。

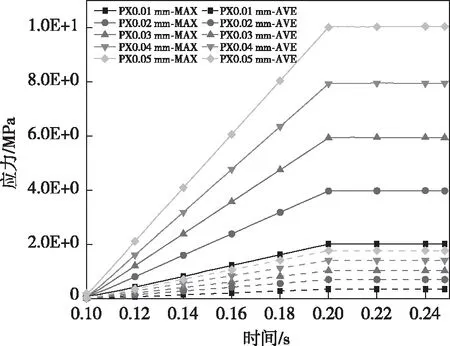
图4 不同偏心距下瓦片最大应力值与平均应力值Fig.4 Maximum and average stress values of tiles under different eccentricity

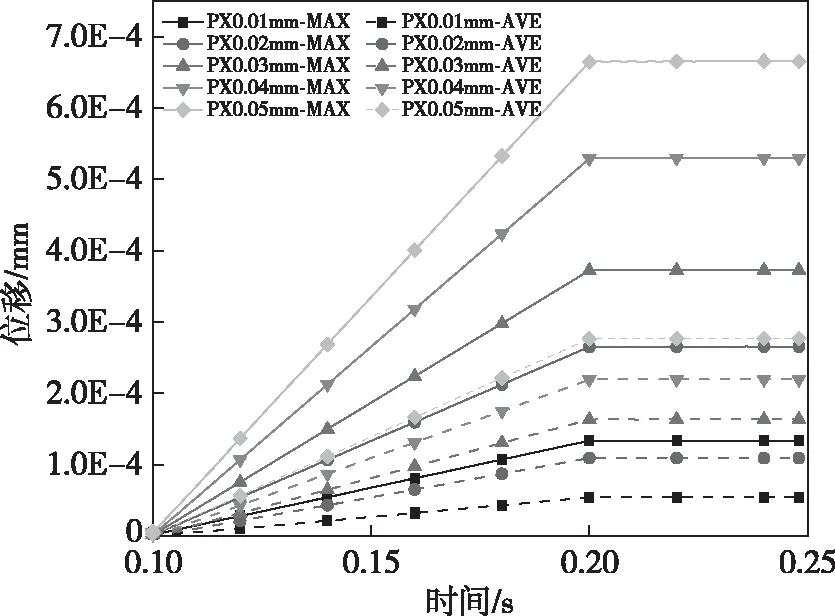
图5 不同偏心距下瓦片最大形变值与平均形变值Fig.5 Maximum deformation value and average deformation value of tiles under different eccentricity

图6为1号瓦片在主轴偏心0.01、0.03、0.05 mm时的应力云图对比图。从图中可以看出，轴瓦受到应力最大值主要集中分布在轴瓦中心的两侧位置处，靠近瓦面边缘和中心的位置受力很小。图7为轴颈表面在主轴偏心0.01、0.03、0.05 mm时的应力云图对比图。可以看出，轴瓦所对应的轴颈位置应力较大，轴瓦之间空隙位置对应的轴颈区域应力相对较小。

图6 1号轴瓦应力云图(从上至下：偏心距分别为0.01、0.03、0.0 5mm)Fig.6 Stress nephogram of No.1 bearing bush(from top to bottom: the eccentricity is 0.01, 0.03, 0.05 mm respectively)

图7 轴颈表面应力云图(从上至下：偏心距分别为0.01、0.03、0.05 mm)Fig.7 Stress nephogram of journal surface (from top to bottom: the eccentricity is 0.01, 0.03, 0.05 mm respectively)

3 结论

基于双向流固耦合分析方法，分析了轴瓦数、油膜间隙厚度、主轴偏心距离对轴瓦和轴颈应力和形变量的影响规律。主要结论如下：

1)当主轴发生偏心、对轴瓦产生过大的压力时，可以考虑采用适当增加瓦块数的方式来改善单个瓦块所承载的应力峰值。

2)轴瓦应力对油膜间隙厚度变化不敏感。

3)主轴偏心距离增大，会对轴瓦局部造成较大压力；偏心越大，会使轴瓦的形变峰值显著增加，应预防轴瓦变形过大而引起破坏。

4)主轴轴系发生偏心时，主要对轴瓦的中心产生较大的压力，对轴瓦边缘的压力很小，轴瓦中心主要承载主轴偏心时的径向力。