协变量缺失的乘积模型的加权LPRE估计

刘惠篮

(贵州大学 数学与统计学院，贵州 贵阳 550025)

乘积模型是一类重要的参数模型，能够处理非负响应变量的情况，具体形式如下：

(1)

其中:Xi为p×1维协变量，β0为p×1维真实的未知参数向量，Yi为正响应变量，εi为正的随机误差。现实中，很多情况下数据处理者更加关注的是相对误差，而非绝对误差，参见文献[1]。针对乘积模型，CHEN等(2016)[2]通过最小化乘积相对误差LPRE(least product relative error)损失函数

(2)

得到了β0的LPRE估计。注意到式(2)经简单计算可化简为

(3)

近年来，学者们基于LPRE方法，研究了参数、非参数及半参数乘积模型，参见文献[3-10]。

又由于现实中，往往存在缺失数据的情况。其中，随机缺失(missing at random，MAR)是缺失数据中的一种常见的缺失机制，参见文献[11]。考虑协变量缺失的情况，令δi为标识协变量Xi是否缺失的示性函数，即

本文中假定协变量Xi随机缺失，即缺失概率仅依赖于可观测的变量Yi，而不依赖于缺失变量Xi，即

P(δi=1|Xi,Yi)=P(δi=1|Yi)=π(Yi)=πi

(4)

针对协变量缺失的回归模型，已有一些学者进行了研究。2011年，杨[12]基于经验似然方法，研究了协变量随机缺失的线性模型的参数的置信区域构造问题。2012年，李[13]基于最小二乘、逆概率加权(inverse probability weight,IPW)及局部核光滑方法，研究了协变量随机缺失的单指标模型的估计问题。2016年，刘[14]在不完整数据下，结合复合分位数方法，研究了参数及半参数模型的估计的统计性质。

然而，还未有学者在相对误差LPRE的视角下，研究协变量随机缺失的乘积模型。因此，作者结合LPRE、IPW与非参数核估计方法，研究协变量随机缺失的乘积模型。

1 估计方法

(5)

得到的估计，定义为LPRE-CC估计。然而，在协变量随机缺失时，基于CC方法得到的估计是有偏的[13-14]。因此，结合IPW与LPRE方法，考虑最小化目标函数

(6)

得到的估计定义为LPRE-IPW估计。注意到πi的形式是未知的，需要对其进行估计。又由于πi=π(Yi)=P(δi=1|Yi)=E(δi|Yi)，因此可使用非参数核估计(Nadaraya-Waston方法[15-16])对其进行估计，即

(7)

其中：Kh(·)=K(·/h)，K(·)为核函数，h为窗宽参数。将式(7)带入式(6)，得到目标函数

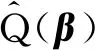
2 理论性质

为了证明LPRE-IPW和LPRE-NIPW估计的渐近正态性，需要如下的一些假定条件：

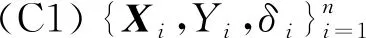
(C2)K(·)为二阶有界核函数；

(C3)π(y)和密度函数fY(y)在Y的支撑集上具有二阶有界导数，且π(y)≥C,C是一个正常数；

(C5) 矩阵A=E[(ε+ε-1)XXT]为正定矩阵；

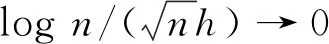
首先，讨论LPRE-IPW的渐近正态性。

定理1假定条件(C1)—(C5)成立，则有

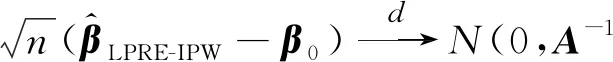
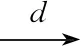
且

A=E[(ε+ε-1)XXT]

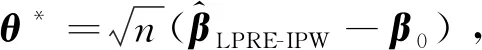
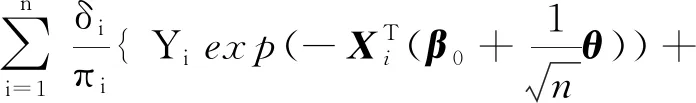
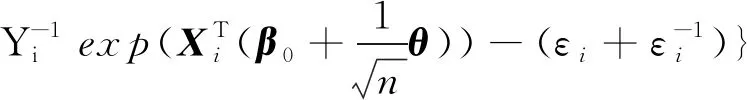
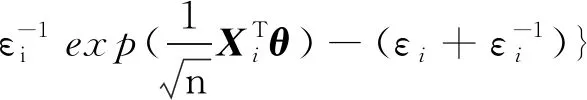
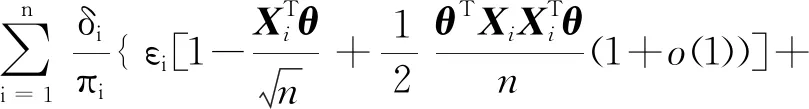
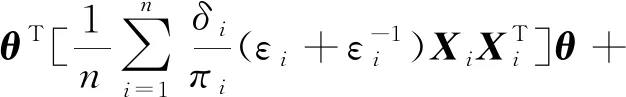
注意到An=A+op(1)，由二次逼近定理[17]知

θ*=-A-1Wn+op(1)

再由中心极限定理，可知

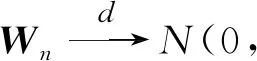
其中，

因此，

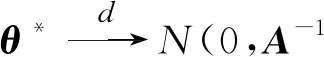
定理1得证。

对任意矩阵M，记M⊗2=MMT。下面，讨论LPRE-NIPW估计的渐近正态性。

定理2假定条件(C1)—(C6)成立，则有

其中，A=E[(ε+ε-1)XXT],且

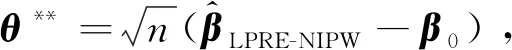
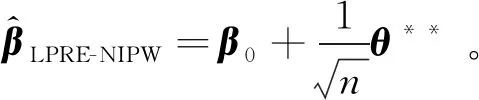
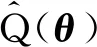
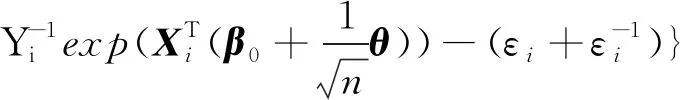
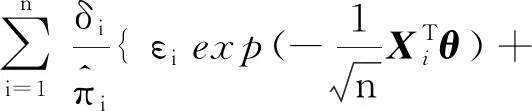
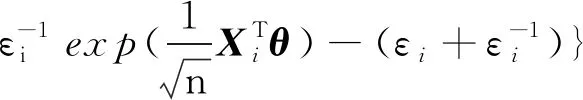
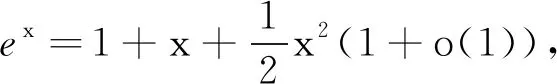
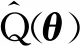
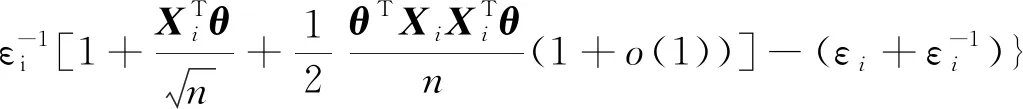
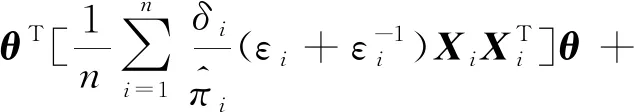
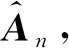
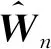
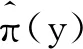
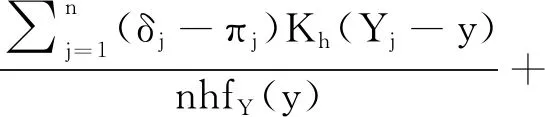
因此，有

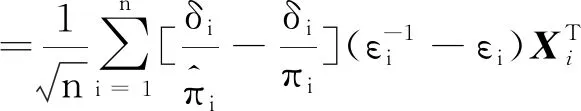
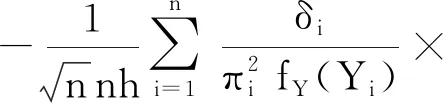
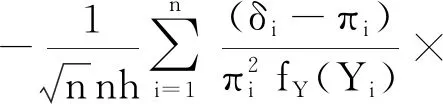
op(1)

对于Wn2，有

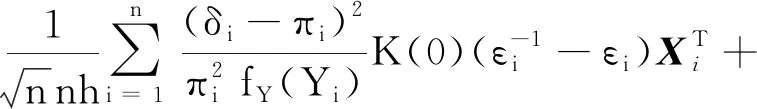
=op(1)

对于Wn3，有

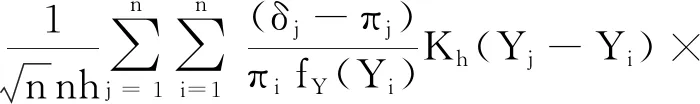
综上，可知

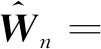
再由中心极限定理，可知

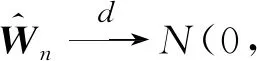
其中,

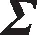
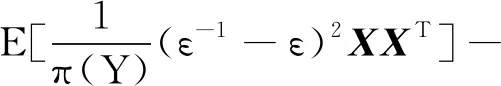
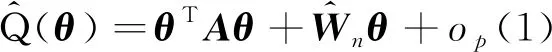
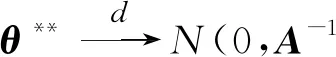
定理2得证。

注结合定理1和定理2，可知

3 模拟仿真

通过数值实验，比较LPRE-CC、LPRE-IPW和LPRE-NIPW方法在协变量随机缺失的乘积模型下的表现。核函数取为高斯核函数。具体模型生成如下：

Y=exp(Xβ0)ε

其中:X=(X1,X2)，X1来自于均值为1且方差为1的正态分布，X2来自于(0,1)区间的均匀分布，β0=(β01,β02)=(1,2)。随机误差ε考虑两种情况：

1)ε～f1(x)，即ε来自于密度函数为f1(x)=c1exp(-x-x-1-logx+2)I(x>0)的分布，其中，c1是正则化常数，用于保证密度函数在定义域上积分后等于1；

2) logε～U(-1,1)，即ε=expζ，其中，ζ服从均匀分布U(-1,1)。

以上两种误差分布均满足条件(C4)。针对数据缺失，考虑两种缺失概率：

1)P(δ=1|Y)=1/(1+0.2exp(0.2Y-4))，此时协变量X的平均缺失率约为17%；

2)P(δ=1|Y)=1/(1+0.2exp(0.1Y-1))，此时X的平均缺失率约为27%。

考虑样本量n=100和n=200。本例中，为了节约运行时间，令h=1.5×n-1/3，其中，n为样本量。此时，窗宽满足条件(C6)。为了比较不同估计的表现，记录了估计的经验偏差(Bias)、样本标准差(standard deviation，SD)和均方误差(mean square error，MSE)3个指标。各种情况均重复试验2 000次。模拟结果记录于表1和表2中。

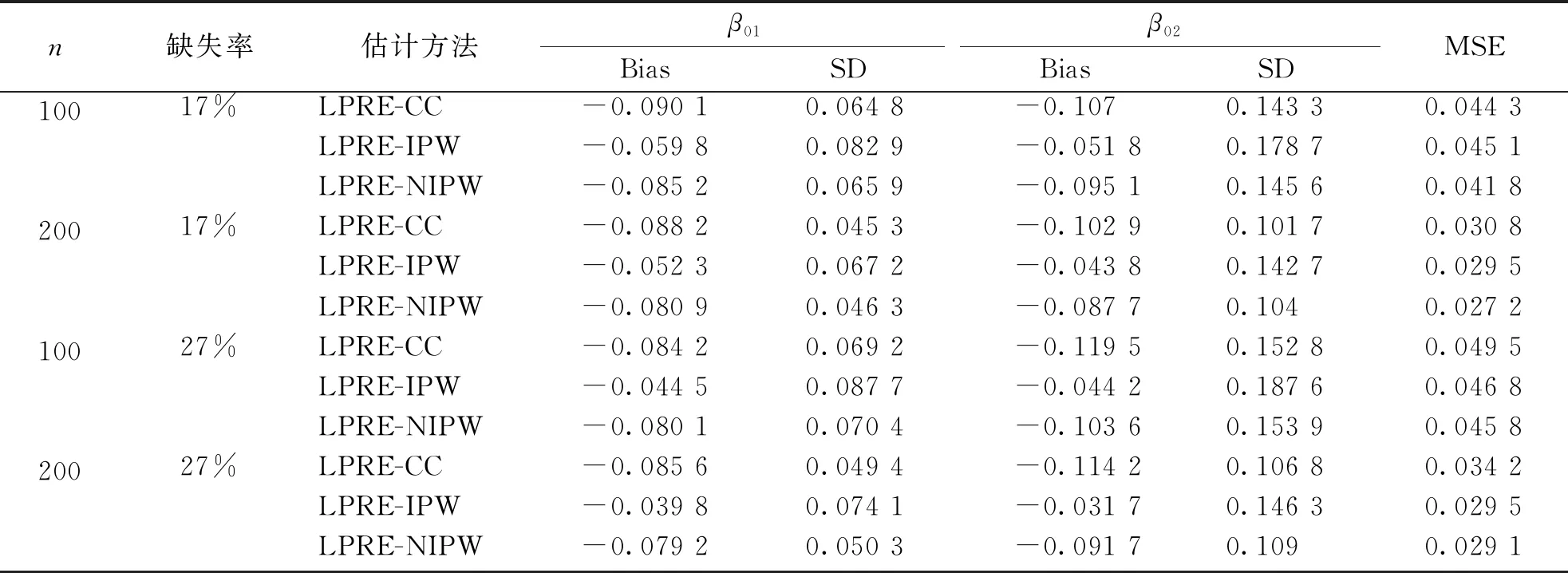
表1 ε～f1(x)时LPRE-CC、LPRE-IPW和LPRE-NIPW的模拟结果 Tab.1 Simulation results for LPRE-CC, LPRE-IPW and LPRE-NIPW when ε～f1(x)

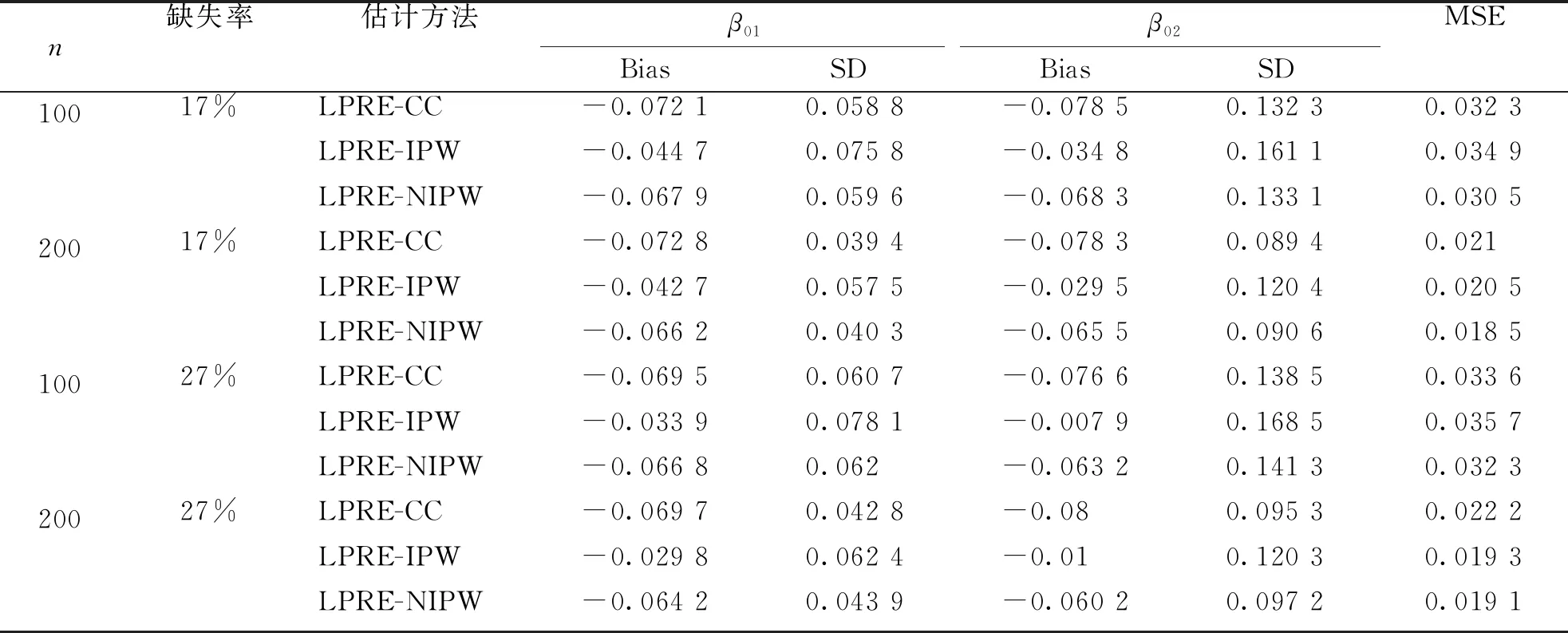
表2 log ε～U(-1,1)时LPRE-CC、LPRE-IPW和LPRE-NIPW的模拟结果Tab.2 Simulation results for LPRE-CC, LPRE-IPW and LPRE-NIPW when log ε～U(-1,1)

由表1和表2可以看到，在各种误差分布、缺失率及样本量下，由于LPRE-CC估计是有偏估计，LPRE-CC具有较大的Bias，因此导致MSE也较大；LPRE-NIPW和LPRE-IPW相比，具有较小的SD，该结果和定理2的结论是一致的；LPRE-NIPW与LPRE-CC和LPRE-IPW方法相比，具有最小的MSE，也就是说LPRE-NIPW方法比其他两种方法更有效。再有，固定样本量，随着缺失率的增加，3种方法的MSE都增大，即估计效果都变差；固定缺失率，随着样本量的增加，3种方法的MSE都减小，即估计效果都变好。

值得注意的是，现实中由于真实的选择概率是未知的，因此LPRE-IPW估计实际上是不可获取的。LPRE-NIPW方法在使用非参数估计方法估计选择概率时由于使用了更多的样本信息，估计效果优于LPRE-IPW方法。综上，可知使用LPRE-NIPW方法估计协变量随机缺失的乘积模型的未知参数具有较好的效果。

4 总结