基于改进粒子群的季节性风电出力场景预测

孙理昊

（北京科东电力控制系统有限责任公司通讯与安全分公司网络安全集成部 北京市 100192）

在可持续，绿色发展的前提下，风能作为一种的可再生的清洁能源，在电网中所占的比重逐年上升。然而，风能具有很强的随机性、地域性、波动性以及不确定性，这对风电大规模并网提出了巨大挑战。在能源发展新形势下，为降低风电并网对配电网的不良影响，加强其接入电网的积极作用，要对风电接入配电网时的出力预测进行研究。

目前，新能源并网已经成文国内外研究的热点。为了对风速预测，文献和文献采用极限学习机（HELM）、差分进化算法（DE）的对LSTM 中的隐藏层数量进行优化以保持学习性能和模型复杂性之间的平衡。Altan A等人基于长短时记忆（LSTM）网络和灰太狼优化器（GWO）分解方法，提出了一种新的混合WSF 非线性，根据从土耳其马尔马拉地区五个风电场收集的数据，采用了开发的非线性混合模型，预测精度上优于单一预测模型。Habib A为了提高短期风电预测精度，利用奇异谱分析将原始风电功率序列分解为趋势分量和波动分量。然后利用最小二乘支持向量机（LSSVM）对趋势分量进行预测，利用深度置信网络（DBN）对波动分量进行预测，研究表明，所提出的组合模型为短期风电预测提供了一种有希望且有效的替代方案。Neshat M一种新的基于复合深度学习的进化方法，用于准确预测风力发电厂的发电量，该算法由自适应差分进化（SaDE）算法和作为超参数优化器的正弦-余弦优化方法组成，然后与称为长短时记忆（LSTM）的递归神经网络（RNN）相结合。取得的预测结果支持了所提出的混合模型在准确预测和计算运行时间方面的优势。

为了提升季节性风电出力场景预测准确性和可靠性，减少风电并网对电网状态的影响。基于深度学习网络模型，以不同季节下的典型风电场景为前提，对其短期的功率进行预测。本文首先对数据进行处理，使得效率和性能得到提升，其次介绍风电预测模型的结构，最后采用智能算法对LSTM模型进行改进，对比分析了LSTM、PSO-LSTM 和IPSOLSTM 预测模型，实验表明，改进的粒子群算法具有最好的预测精度和可靠性，且采用深度学习网络预测处理模型有利于优化经济调度的流程和方案以及负荷增减决策的规划和制定。

1 数据集处理

在采集数据时由于各种突发状况和采集误差等原因，在采集的数据中可能会出现数据缺失异常的情况。因此，若依据采集的原始数据建立预测模型进行分析则会导致结果精度低甚至错误的结论。为了能够提高模型的准确率和有效性，需要对采集的原始数据进行对应的处理，以保证其准确性和完备性。

对于不同的状况采取不同的手段。对于缺失的数据可以采用直接删除然后利用插值补充；而对异常值的处理一般可以分为两步，首先根据对应的检测算法找出异常点，然后根据实际使用进一步对异常值处理。常用的异常检测方法有：聚类分析法、支持向量机异常检测、孤立森林异常检测、高斯异常检测等。为了更加快速简单的处理异常值，本文把异常的数据处理成错误或者丢失的数据，利用缺失数据的一般处理方法整改；然而异常值并不是缺失值，可能含有对系统有用的信息，直接删除会导致数据不完备。因此，在此处利用插值法补充。

在对原数据处理完毕后，首先对数据进行集成，然后把数据按最小-最大归一化的方法进行变换，变换公式如式（1）：

式中：P, P'分别为风电功率和归一化后风电功率，P,P分别表示风电功率的最大和最小值。

对于风电数据这种大规模数据库进行数据分析需要耗费大量的资源和时间。本文利用数据规约技术，能够从原有庞大的风电数据集中得到一个保持原有数据集完整性的精简数据集。此方法提升了效率和性能，并且经计算的结果与原数据基本相同。

数据经过归一化规范后，在预测时还需要恢复成原数据，为了从[0,1]空间映射到实际空间。本文中利用式（2）所示的规约函数进行还原：

式中：P是恢复后的风电功率预测值，p'是还原前的风电功率预测值。

2 改进粒子群的风电出力预测模型

本研究利用改进粒子群算法(Improved particle swarm optimization, IPSO)算法对LSTM 的时间步长、隐藏层单元数和批处理大小进行优化。在进行优化之前，需要对算法进行初始化操作，包括：粒子数、维度以及粒子速度和位置等，并根据各粒子的位置建立LSTM 预测模型，采用平均绝对百分比误差(Mean Absolute Percent Error, MAPE)作为适应度函数。在训练改进粒子群的LSTM 模型时，在本文中，抽出3/5 的数据集用来训练IPSO-LSTM 预测模型，2/5 的数据集用来验证训练的效果，剩余1/5 的数据集则用来测试。采用Adam 算法对LSTM 模型进行训练，损失函数采用均方误差(Mean Square Error, MSE)。IPSO-LSTM 结构示意图如图1 所示。

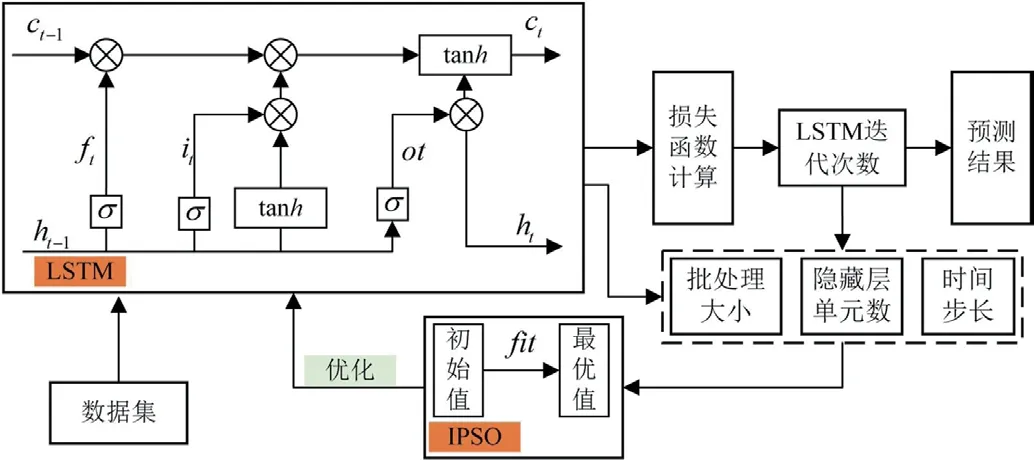
图1：IPSO-LSTM 结构示意图

神经网络的特征提取层(隐藏层)单元的取值在[10,60]动态变化，时间步长的大小保证在区间[1,35]内,批处理大小的范围为[1,50]。粒子群粒子的种群大小为100，最大的迭代次数为300。IPSO 优化LSTM 预测模型的流程图如图2所示。

图2：IPSO 优化LSTM 模型流程图

步骤一：初始化LSTM 网络结构的隐藏层数量、时间步长、批处理大小；并根据LSTM 超参数的设置，对改进的粒子群进行初始化操作。

步骤二：抽出3/5 的数据集对LSTM 网络进行训练，利用测试样本计算预测误差，并将误差实时更新到IPSO。

步骤三：利用式（3），计算各粒子的适应度值，并对种群最优和个体最优的数值进行更新。根据公式（4）、公式（5）更新粒子的惯性权重值和加速因子值，以避免陷入局部最优，进而影响优化结果。

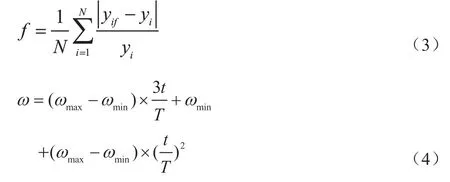
式中：N 为验证数据集大小，y为原验证数据值，y是预测的验证数据；ω, ω为权重的最大值和最小值；c, c为加速度因子的起始值和终止值，其中c表示第一个，c表示第二个；t 是当前的迭代次数，T 是迭代的总次数。

步骤四：根据式（6）和式（7）分别对IPSO 算法中的粒子的速度和位置更新。

步骤五：是否满足要求，当满足要求时，输出最优的参数值；若不满足停止条件时，则返回步骤三，继续执行操作，直到迭代至最大次数。

3 实验结果分析

为了证明IPSO-LSTM 风电功率预测模型的准确性与可靠性。另外选取了LSTM 预测模型、粒子群优化的(PSOLSTM)预测模型作为对比对象。在春夏秋冬四个季节的前提下，选取风电功率出力的典型场景进行计算和分析。四季典型出力场景预测如图3 所示。

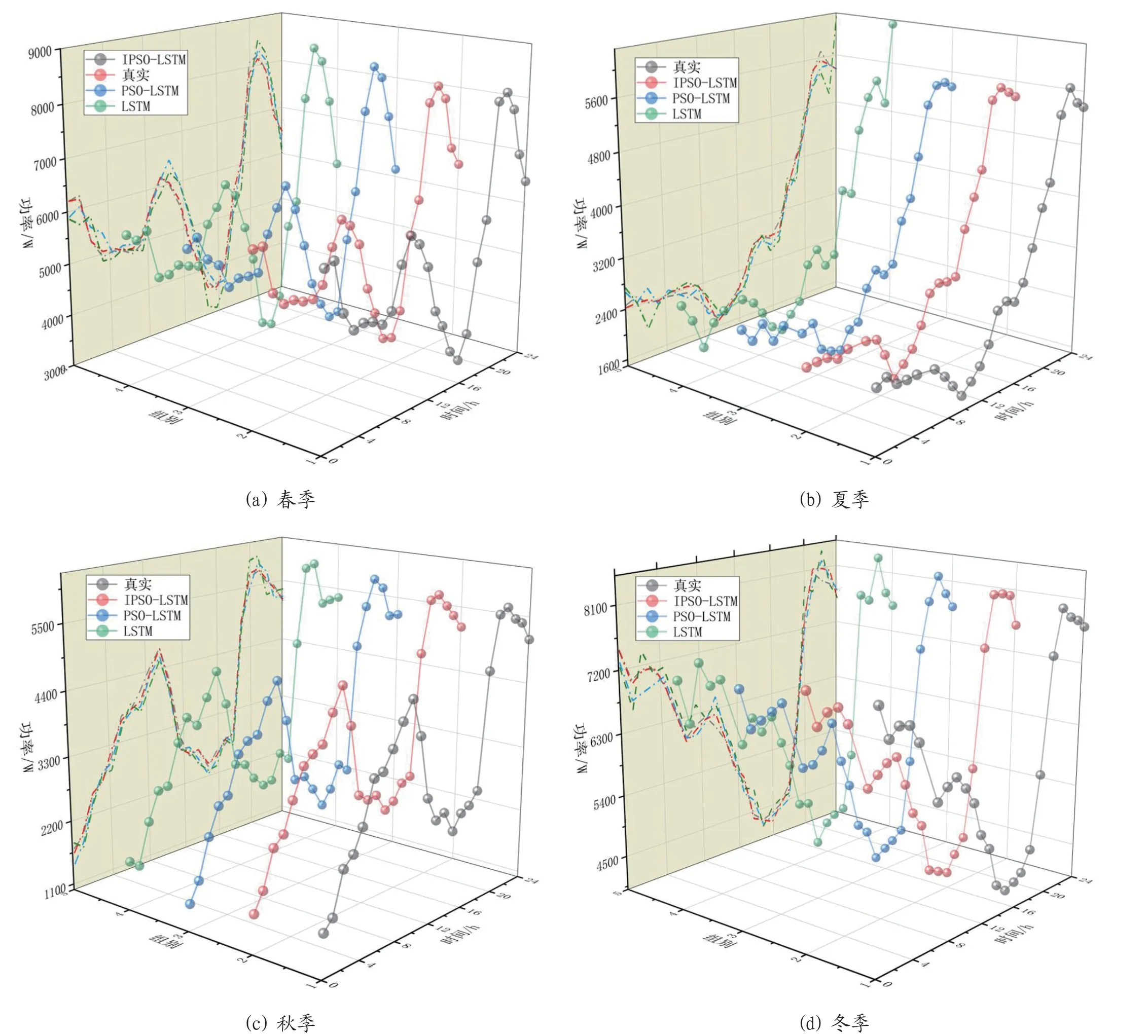
图3：四季典型出力场景预测

从图3 中可以看出，四个季节的风力发电功率出力都存在很大的峰谷差。通过图中预测曲线拟合效果，可以发现各模型对风电功率数据预测的趋势相差不大，但是LSTM 在峰值处具有较大的偏差，拟合效果较差；而IPSO-LSTM 风电功率预测模型具有最高的准确性；PSO-LSTM 和GA-LSTM模型对风电功率预测数据的拟合效果相当，比传统的LSTM拟合程度要好很多。

根据上述分析可知，针对季节性的风电功率预测，基于深度学习网络模型的预测方法有较为理想的预测效果，并且使用PSO、GA 等算法优化后的深度学习网络模型会进一步提升预测精度。然而仅仅通过拟合曲线比较预测效果具有一定局限性，因此，本文采用定量分析的方法，通过数值量化风电功率的预测误差。采用均方根误差(Root Mean Squared Error, RMSE)指标、MAE 指标和MAPE 指标三个指标作为预测模型的评价指标。

根据不同风电功率预测模型在四个季节的误差，对四个季节的误差进行加权平均 计算，并将计算的结果作为每个模型的最终误差结果值，不同模型在3 种评价指标下的误差值如表1 所示。

表1：LSTM 模型预测结果

从表1 中可以看出，针对RMSE 模型评价指标，IPSOLSTM 均方根误差为0.34，比LSTM 和PSO-LSTM 分别降低了74.4%和34.6%。针对MAE 模型评价指标，IPSOLSTM 比其他两种方法分别降低了73.2%、37.5%。同样的，针对MAPE 模型评价指标，IPSO-LSTM 则分别降低了1.82%和1.5。通过以上分析，可以得到：改进的粒子群算法优化LSTM 模型预测误差最小，精确度最大，并且改进的粒子群算法比起其他为改进的算法具有较大的提升；此外，虽然使用不改进的优化算法能提高预测的精确率，但是在要求预测精度的场景内，则不能使用，进一步显现了改进算法的优势。

4 结论

本文采用深度学习网络模型对不同季节性下典型场景风电功率的短期预测，对比分析了LSTM、PSO-LSTM 和IPSO-LSTM 预测模型在准确性和可靠性方面差别。结果表明：IPSO-LSTM 预测模型具有最小的预测误差和最高的可靠性，且采用深度学习网络预测处理模型有利于经济负荷调度计划和负荷增减决策的制定。