例析函数解析式的集中求法

沈峥铃

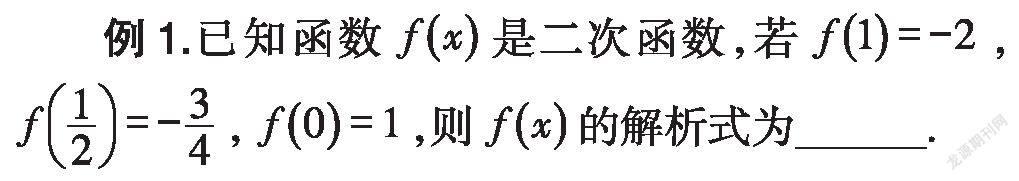
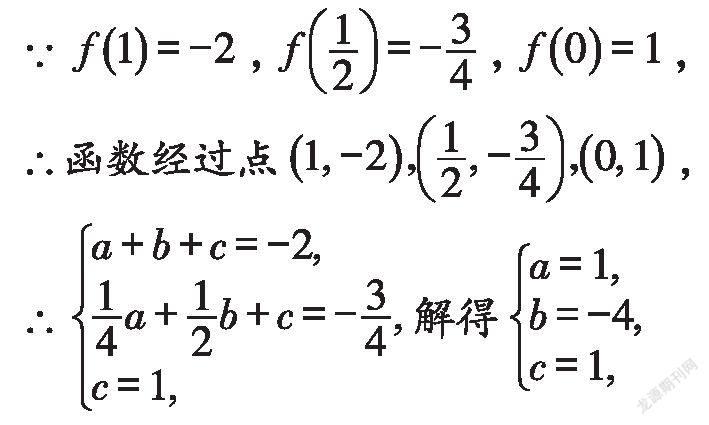
函数的解析式是表示函数的重要方法之一.函数式中通常含有自变量、因变量、参数、常数.不同类型的函数有不同的解析式，如指数函数的解析式为y=a，二次函数的解析式为y=ax+bx+c.本文重点谈一谈

函数解析式的几种求法.

一、待定系数法

分析：由于已知函数的类型，所以可直接采用待定系数法.设二次函数的解析式为f（x）=ax+bx+c，然后将已知条件代入，建立关于系数a、b、c的方程组，解方程组，就能求得函数的解析式.

解：∵f（x）是二次函数，

∴设f（x）=ax+bx+c，

∴函数的解析式为f（x）=x-4x+1.

∴设f（x）-a（x-h）+k，

∵函数f（x）经过点（0，1），（4，1），

∴函数f（x）的图象关于直线x=2对称，

∴函数f（x）的顶点为（2，3），

∴f（x）=a（x-2）+3，

由于已知函数的类型，且函数的顶点坐标很容易求出，所以采用待定系数法，设出二次函数的顶点式，然后将已知条件代入，求得待定系数的值，即可得到解析式.

二、配凑法

配凑法通常用于求复合函数的解析式.若已知f（g（x））的表达式，可采用配凑法，将其表达式配凑成g（x）的倍数或平方式，然后用x替换g（x），即可求得f（x）的表达式，便能得到函数f（x）的解析式.

则f（x）=x-2x，

因此函数的解析式为f（x）=x-2x.

则f（x）=x+1，

故函数的解析式为f（x）=x+1.

运用配凑法求函数的解析式，需通過观察，发现f（g（x））的表达式与g（x）的表达式之间的联系，再进行合理的配凑.

三、换元法

有些复合函数的表达式较为复杂，很难通过配凑求得函数的解析式，此时需采用换元法求解.首先把复合函数f（g（x））中的g（x）用一个新元t替换，并用t表示出f（g（x）），得到关于t的表达式，再用x替换t，就能得到函数f（x）的解析式.

则f（x）=x-x+1

故函数的解析式为f（x）=x-x+1.

解：设t=2x+1，

求函数的解析式问题虽然难度不大，但是题型多变，且具有较强的抽象性.因此同学们在平时的学习中要熟悉各类题型，掌握一些常用的解法，如待定系数法、配凑法、换元法等，学会根据题目中的条件，选择与之相应的方法进行求解.