复杂介质结构电气设备的FDTD 算法∗

聂睿瑞 李 勃

(1.南京信息职业技术学院智能交通学院，江苏 南京 210023；2.南京航空航天大学无人机研究院，江苏 南京 210016)

在现有的电磁场算法中，时域有限差分法FDTD的使用越来越广泛[1－4]。因为没有引入数学计算，传统FDTD 运算法则的网格划分较为简单。然而，需要解决曲面问题时，传统FDTD 算法就不太适用了。对于电气设备的不连续曲线表面和多重材料结构，传统FDTD 算法还会产生发散和不稳定现象。所以，很多项目都把FDTD 算法的稳定性作为研究重点[5－7]。

本文提出了一种基于非标准曲线算子的三维高阶FDTD 算法，可以用于解决复杂介质结构电气设备的电磁兼容问题。该三维高阶FDTD 算法使用了足够多的点来表示空间微商，而不是像传统FDTD算法那样只取两个点。在完全导体边界或吸收边界处，空间模板不可避免的会扩大，采用紧凑的曲线差分方案，能将无限空间转换为修正过的PML 吸收边界条件[8－9]。考虑到那些界面和任何网格都不相符的材料，该算法使用了特殊的转换法。通过对多种三维曲线以及不同介质结构的电磁兼容性计算，结果表明该方法是有效的。

1 高阶非标准FDTD 算法

1.1 非标准形状的结构

三维高阶FDTD 算法采用式(1)来描述三维电磁场的结构[10]:

式中:g是三维坐标函数；CS是修正函数；Rm和Pm是稳定性参数；Dq是最佳节点算子。q是常规坐标系(u，v，w)的变量，M表示准确度的阶数。该差分法能有效降低色差的影响。而且，只要参数和满足式(2)和式(3)，就可以确定几何细节及场量分配的稳定性。

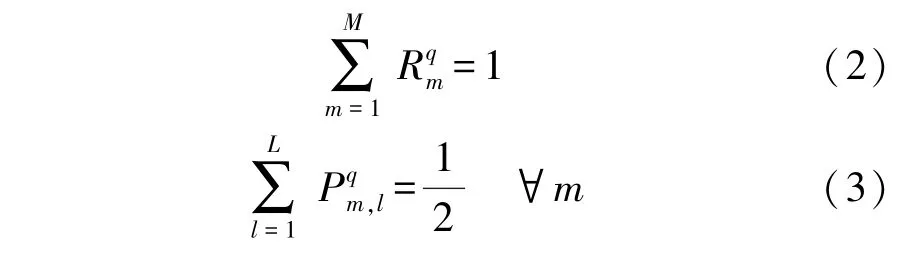
式中:L因子表示模板的数量，一般取L＝3，lδq表示各轴上的坐标。修正函数CS(klδq)用于确保从连续到离散的平滑过渡，其幅度取决于波数k，对网格电磁向量进行傅立叶变换可以得出，CS一般由式(4)求得:

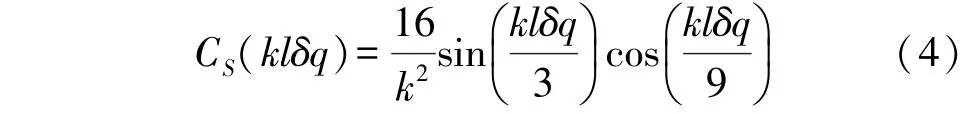
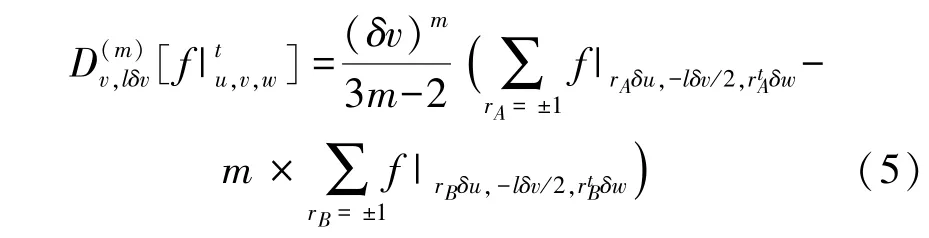
式中:rA、rB是三维计算因子。

同样可以推出在方向u和方向w上的方程。

高阶非标准算子可以应用到麦克斯韦旋度方程中的空间微商和时间微商的离散化中。根据其近似程度，通过一组参数关系式能够得出基本模型。

空间微商:

时间微商:

式中:∂m是微分参数，CT(δt)是T[·]的修正函数，b1和b2是特定的调节参数。除了全导电墙，式(7)在域中处处适用。对于PEC wall，其模板在格点的两侧都会至少延伸两个节点。相应的曲线压缩公式为:

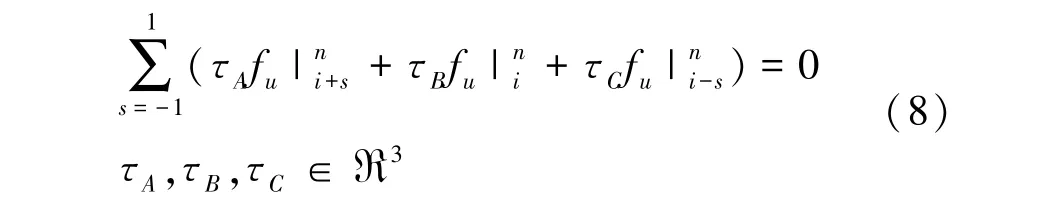
式中:τA，τB，τC是三维离散积分系数；S是将曲线从三维压缩到二维的参数。

此方程可自适应于曲率的变化，对连续物理空间进行离散化，转换为二重拓扑网格结构。

1.2 非正交二重网格

将给定三维区域按照坐标系(u＝iδu，v＝jδv，w＝kδw)进行划分，如图1 所示。各个主单元的中心是(i，j，k)，而第二重单元的中心则是主单元的顶点。磁场向量H(位于主表面的中心)的共变量hq以及逆变量hp和电场向量E(位于边缘的中心)的共变量eq以及逆变量ep相互交错。

图1 FDTD 二重网格划分图

我们是根据表面的场通量可定义为f(p)＝g1/2f(p)(f是电场或磁场)来进行这样的划分，其中gpq为坐标系的度量。由FDTD 原理可知，fq＝gqp fp且fp＝gpqfq。再引入线性算子Q(p)，得到f(p)＝Q(p)[fq]，式中用到原有分量fq及相邻分量fq＋1和fq＋2(q＋1、q＋2表示u、v、w的连续循环)。比如u轴上Q(u)[hu]的表达式是:

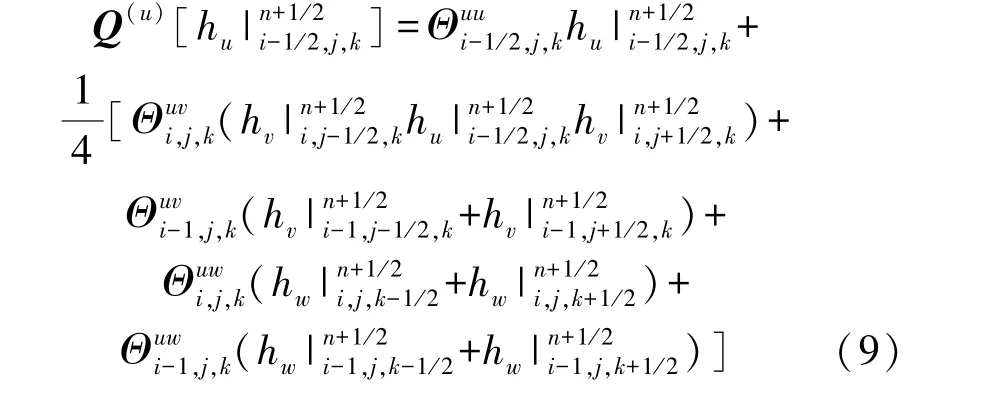
式中:Θpq＝g1/2gpq，因为省略了二重交叉场复杂的投影分量，这样对通量的分析就相对简便。通过以上步骤并替换旋度算子，可将安培和法拉第定律写为:

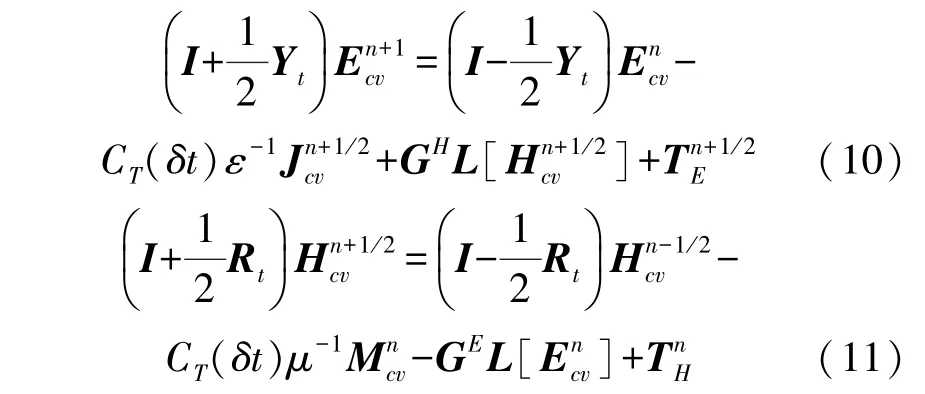
上式中Ecv＝[eu ev ew]和Hcv＝[hu hv hw]是未知共变分量的矩阵；L＝[Lu，Lv，Lw]为空间算子；J＝σE和M＝σ∗H是对应的传导电流密度；Yt和Rt是定义每个介质表面的基本矩阵；GH，GE是合适的度量张量，μ是磁导率。矩阵TE和TH根据T[·]集合了所有的高阶临时微商，且容许修正。因为式(10)和(11)把所有的高阶临时微商都聚集到一个矩阵中，这样就能利用临时储存向量通过修正广义跳点法把每个时间步长分成和阶数相同的数量。

采用冯诺依曼分析法来分析式(6)和式(7)的稳定性，可知:

可调节的准确度系数M和L极大地改善了色散关系。把高阶非标准FDTD 算法的色散关系和二阶Yee 单元进行比较，经数学运算有:

由此看出上式只是普通FDTD 关系FFDTD(·)中很小的一部分。例如，取M＝4，L＝3，c′是相速度的数值，β＝2π/(kδw)，θ为入射角时，有:

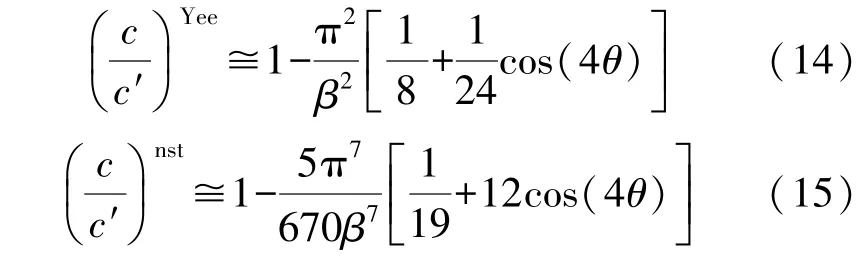
式中:nst的含义是非标准。

合适的和分量取值使得色散关系得到了明显提高。高阶非标准FDTD 算法能够改善后续计算的不稳定性、减小色散误差且无需使用共形技术。基于整体场的实现，发散的问题可采用曲线非标准PML 边界条件来解决。选用合理的缩放比例，保持原场变化，进行合适的坐标变换，就能达到最优吸收边界条件。

1.3 空间低通滤波过程

由于对介质表面采取了不定的调整，高阶非标准FDTD 算法的不稳定因素就是不均匀的网格划分方式。而消除寄生高频成分是一个可行的应对办法。因此，我们可以对单元平均值采取后期处理:

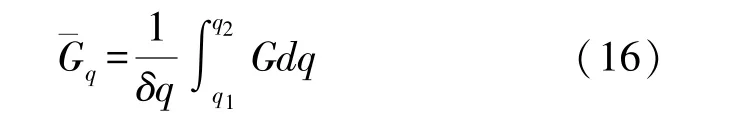
式中:单元边界[u1，u2]、[v1，v2]和[w1，w2]的维数表示为[q1，q2]集合，G是向量Ecv和Hcv的任意分量。对于多重空间，该式可以在网格的u、v、w方向上逐一应用。再引入自由度的附加度Ξ来控制滤波，则域的内部可记为:

式(17)的频率响应为:

由式(17)的均衡性可知，FS(k)为实数，滤波只改变场的幅度。为了能够抑制最高频，要求FS(k)＝0。一般取Ξ的值为4，且ζf＝0.351 4、a1＝1.287 587 493 5、a2＝－1.923 789 646 3、a3＝2.575 179 324 9、a4＝0.346 821 379 6。

1.4 介质跳变边界的收敛处理

如果对曲线介质表面的不连续性没有采用合适的跳变条件，就会产生不同的相速度和波长，这会明显影响FDTD 算法的稳定性和收敛性。并且，电磁场在这些边界上产生不连续，即便对该区域采用平滑处理方法，最终的模拟结果仍然会出现极大的偏差。

对于图2 中所示的介质曲面，取＝(，，)T为单位向量。任意两个区域(mat ＝A，B)中，如果决定了分辨度就定义了特定的空间值。由此，Emat和Hmat向量就能通过合适的切线或普通连续条件从该介质的εmat和μmat中得出。选用一系列的协变分量，表面∂w、hu的修正为:

图2 介质曲面处理

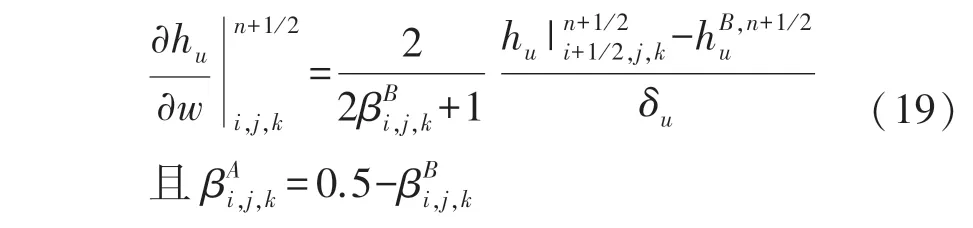
式中:hu可以通过下式算出:

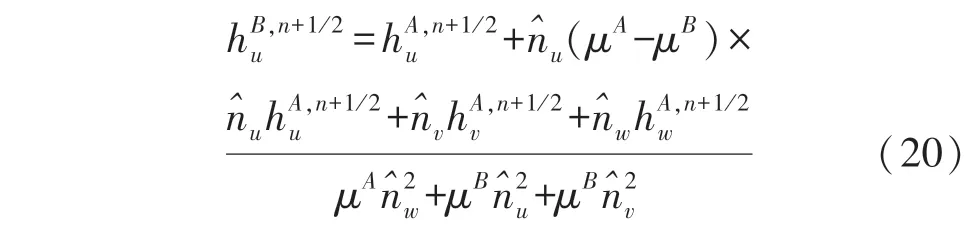
式(20)的三种普通变形推算为:

对于e分量而言，表达式也类似。对式(22)、(23)的非变量有:

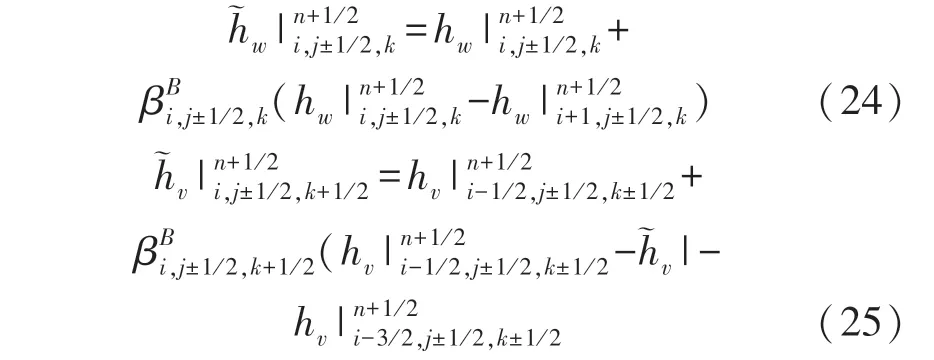
式(19)～(25)预先修正了高阶非标准FDTD 算法，这使麦克斯韦方程在整个域中都是可解的，从而大大提高了对曲线表面的计算准确度。

2 试验与仿真

设计图3 中所示的某机电设备电路板，将集成电路安装在第一层板上，它们由相同的介质构成。介质参数分别为:εA＝2.5ε0，μA＝1.76μ0，σA＝0.22 S/m。基片的参数是:εB＝4.7ε0，μB＝μ0，σB＝0.03 S/m。对于该机电设备电路板，在建模时需要考虑损耗以及0.01 F 的去耦电容在回路中所产生的高频能量。该电路板尺寸为:b1＝18.65 mm，b2＝16.93 mm，b3＝2.5 mm。把整个区域划分为36×24×8 个单元，取δx＝δy＝δz＝1.5 mm，δt＝25.32 ps。

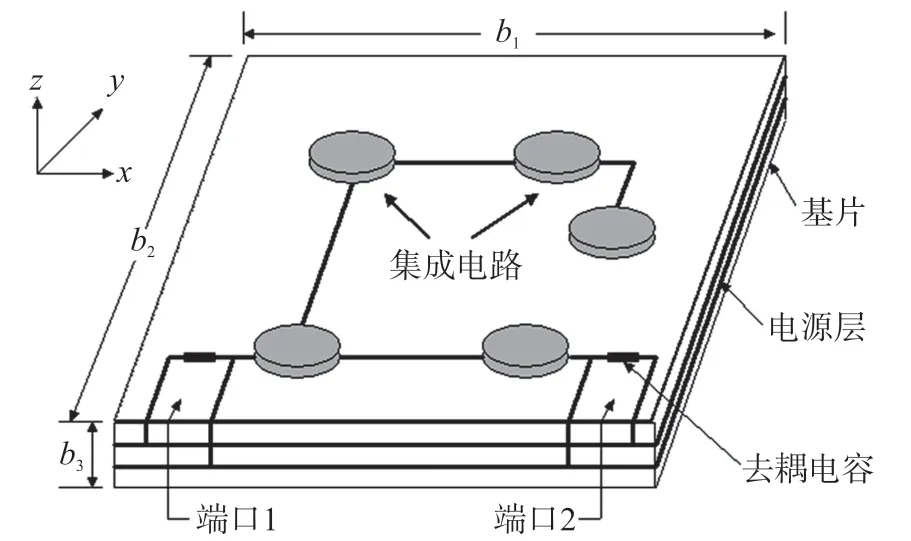
图3 试验用某机电设备电路板

图4 和图5 分别显示出参量S11(端口1 上的辐射)和S21(两个端口之间的辐射)随频率变化时，二阶FDTD 算法和高阶非标准FDTD 算法的仿真结果。从图4 中可以看出，高阶非标准FDTD 算法的准确度非常高，并且没有出现任何色散情况。相反的，尽管Yee 算法采用了标准的82×64×156 网格，却不能计算出准确的峰值。

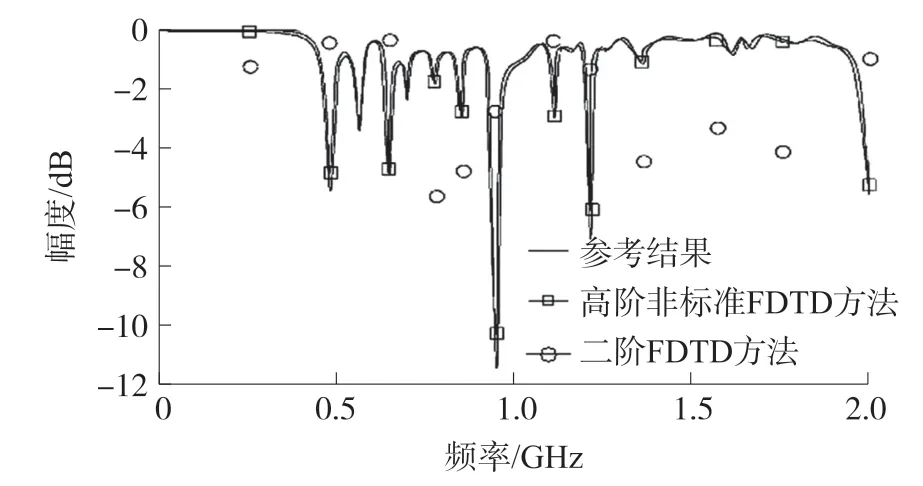
图4 S11的幅度

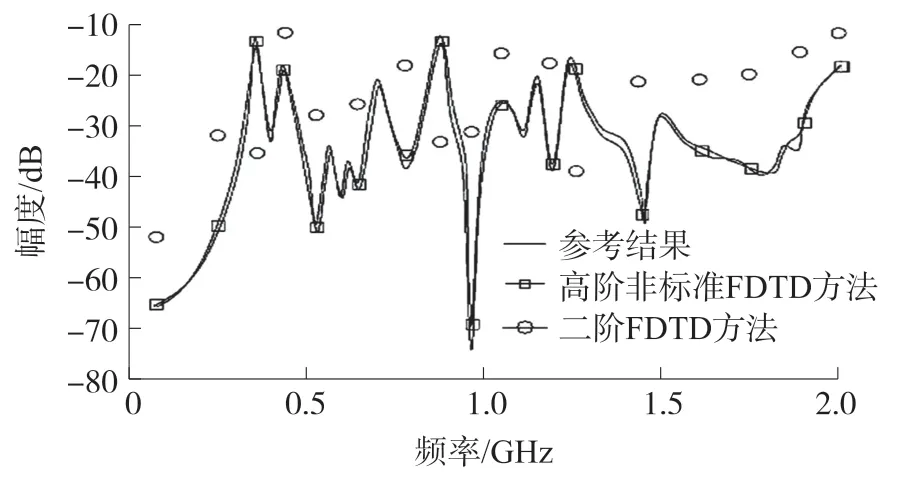
图5 S21的幅度

最后，图6 中显示出不同的离散化程度下，在电路板某固定位置处的标准化相速度。

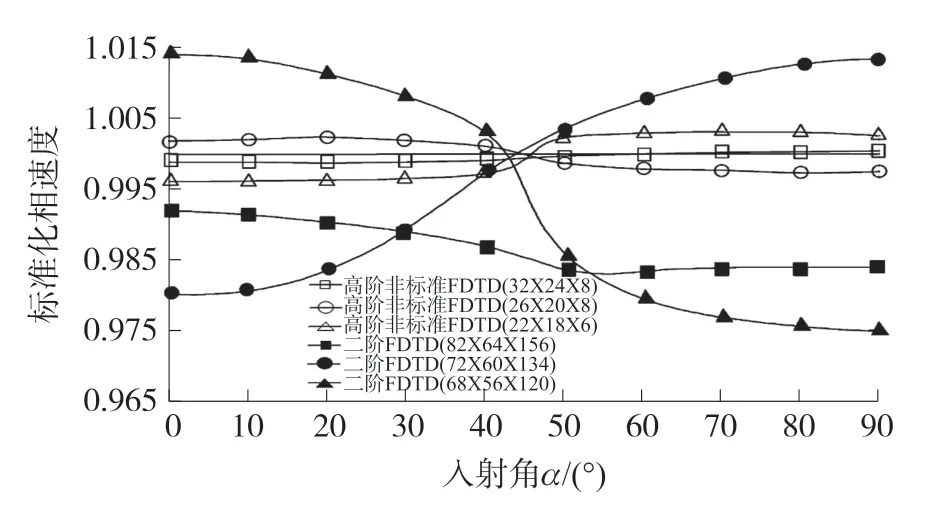
图6 多种FDTD 方法计算的相速度对比

3 结论

结果表明，本文所提出的基于非标准曲线算子的三维高阶FDTD 算法，其计算结果比二阶FDTD算法要精确。因为随着分辨度的下降，二阶FDTD会严重偏离实际值。所以在分析较大结构的EMC问题时，采用高阶FDTD 算法能够较好地弥补传统方法在准确度方面的缺陷。此外，高阶非标准FDTD 算法还可以节省大约85%的CPU 及内存。