基于滑模和控制分配的航天器RCS容错控制

信玉暄，辛万青，王 勇

(1.北京宇航系统工程研究所，北京 100076； 2.中国运载火箭技术研究院， 北京 100076)

1 引言

RCS主要应用于航天器中，指利用执行器排出的工质产生反作用力形成控制力或力矩的动力系统。随着航天科技的发展，航天器执行任务要求越来越高，动力系统组成越来越复杂，RCS故障逐渐成为影响航天器任务完成可靠性的关键因素之一。在系统发生故障后，有效进行容错控制，可以提升航天器在故障下的任务完成能力。RCS由喷管组成，其执行器数量大于控制通道数量，为一种过驱动系统，其控制器也通常分为控制律和控制分配算法两级。因此可以结合容错控制律设计和控制重分配2种方法实现容错控制。

为使系统在故障时仍能实现有限时间稳定，基于终端滑模控制的容错控制方法由于具有使系统沿滑模面有限时间收敛的特性，被广泛应用于航天器容错控制中。而为了解决控制过程中的奇异问题，文献[8]提出了一种基于非奇异终端滑模(non-singular terminal sliding mode，NTSM)的方法。以上文献中，作者均根据故障信息构造补偿控制律以容忍故障，但未考虑系统控制能力有限的问题。对于RCS，喷管提供的控制力矩有限，若控制律过大，使系统难以提供相匹配的控制力矩，会导致控制性能下降甚至失稳。针对以上问题，文献[10-11]基于滑模控制设计抗饱和容错控制律以补偿执行器控制能力有限对系统造成的影响。文献[12-15]基于终端滑模控制设计有限时间容错控制律并利用饱和函数或Tanh函数对控制律限幅，以匹配控制律与系统控制能力。终端滑模控制中为保证系统状态沿滑模面运动并最终收敛到零，需根据滑模面导数设计等效控制律，但以上文献均将限幅函数作用于控制律整体，限幅后的等效控制律难以保证系统状态沿滑模面收敛到零，因此文献[12-13]仅能保证控制律限幅前的有限时间稳定或固定时间稳定，而文献[14-15]仅能使系统状态有限时间到达滑模面，无法保证其到达滑模面后的有限时间稳定。

控制重分配是一种通过在控制分配过程中引入故障信息进行重分配实现容错控制的方法。其中基于优化的重分配算法不仅可以实现容错控制，还可以优化系统能量消耗，受到学者青睐。但直接力组合系统中，喷管输出控制力与标称控制力间存在一定偏差，造成控制力矩不确定。为处理系统和故障诊断中存在的不确定性，基于优化的鲁棒控制重分配的概念被提出。其中文献[21-22]针对系统不确定性，文献[23-24]针对故障诊断不确定性，设计min-max问题，在不确定性对重分配影响最大时求解使系统能量消耗最小的分配指令。以上文献均将其转化为二阶凸锥问题(second order cone problem，SOCP)求解，但每次求解该问题时需消耗一个较长的时间，难以在线应用。

综合以上分析和讨论，本文针对RCS执行器推力下降故障，提出了一种容错控制方法。首先，基于NTSM设计有限时间限幅容错控制律(fault tolerant control，FTC)。控制律分为等效控制律与趋近律两部分，区别于文献[12-15]，仅对趋近律部分限幅。其中等效控制律保证系统状态沿滑模面有限时间按收敛到零，趋近律保证系统状态有限时间收敛到滑模面。为使控制律与故障后系统剩余控制能力匹配，根据故障设计控制律最大容许幅值，并根据该幅值和等效控制律设计趋近律最大容许幅值，对趋近律限幅。基于Lyaounov理论证明了限幅后控制律仍可以使系统有限时间稳定。在喷管控制力矩存在偏差情况下，给出了一种鲁棒控制重分配算法，建立min-max优化问题，通过对控制力矩偏差求最大实现鲁棒性，通过对喷管开启时间求最小实现推进剂消耗优化，通过引入故障信息重分配控制信号实现容错控制。将该问题转化为线性规划问题求解，提高求解速度便于在线应用。

2 动力学模型

本文的研究对象为某采用RCS的航天器，由布置在航天器周向的姿控喷管组成，如图1中1～12号喷管所示。其中黄色的1～6号喷管代表小推力姿控喷管，绿色的7～12号喷管代表大推力姿控喷管。不同的姿控喷管开启时分别对航天器产生滚转、偏航、俯仰三通道的控制力矩。通过姿控喷管的开闭可以实现航天器的姿态控制。

图1 航天器RCS示意图Fig.1 The RCS

建立系统模型如下式所示:

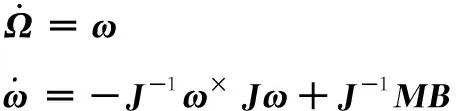
(1)

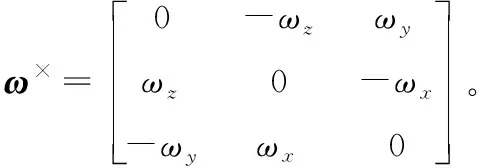
喷管实际输出控制力与标称控制力间存在一定推力偏差，因此其实际输出的控制力矩与标称力矩间也会存在偏差，因此实际上：

=+Δ

(2)

其中:为标称控制力矩，Δ为执行器输出控制力矩不确定性。

令=，=，()=-，=则系统模型变为:

(3)

令矩阵为故障矩阵，当系统无故障时=diag(,,…,)，为单位阵。当第个喷管发生常闭故障时，矩阵中相应元素置0，即=0，当第个喷管发生推力下降故障时，矩阵中相应元素置下降程度(0<<1)。则系统模型如下：

(4)

1控制过程中大小推力姿控喷管不会同时开启，设定一开关门限threshold，当三通道控制律均在threshold以内时仅开启小喷管，其余情况仅开启大喷管。

2下文中下标i均表示该向量在滚转、偏航、俯仰3个通道中的分量，符号“·”表示点乘。

3 容错控制方法

本文的研究对象为过驱动系统，因此其控制器分为控制律和控制分配算法两级。本文首先基于NTSM设计一种限幅有限时间FTC，随后给出一种鲁棒控制重分配算法，并给出一种求解方法。

3.1 基于非奇异终端滑模的控制律设计

首先设计每一个通道的最大容许幅值。针对每一个通道，RCS健康时能提供的最大标称控制力矩如表1所示。

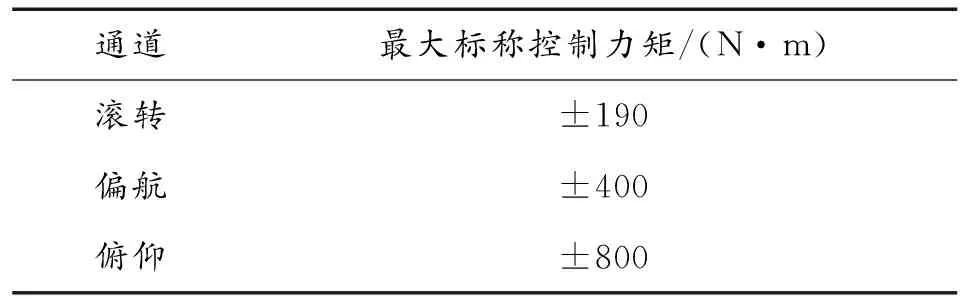
表1 RCS能提供的最大控制力矩Table 1 The maximum control torques that the RCS can provide

为保证滚转通道控制效果，在系统健康时令控制律中俯仰通道最大容许幅值为400，因此得到系统健康时滚转、俯仰、偏航控制律最大容许幅值为

=[190,-190,400,-400,400,-400]

(5)

喷管发生推力下降故障时，需根据系统剩余控制能力重构最大容许幅值，使其与系统剩余控制能力匹配，以达到更好的控制性能。

喷管故障时，系统控制能力变化Δ为

Δ=(-)

(6)

此时重构最大容许幅值：

2=2+Δ(Δ> 0)

2-1=2-1+Δ(Δ< 0)

(7)

即为重构后的最大容许幅值。

下面设计根据最大容许幅值设计限幅有限时间FTC。首先给出控制律的形式如下：

=+

(8)

其次设计等效控制律，选择非奇异终端滑模控制面如下：

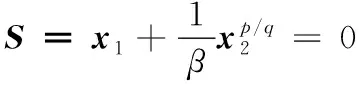
(9)

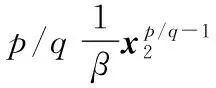
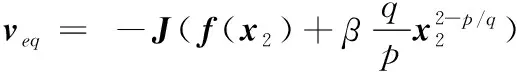
(10)

由于有界，因此知等效控制律有界，且可通过设计参数使等效控制律在最大容许幅值内。

为使系统状态在有限时间到达滑模面，设计趋近律为

(11)

限制趋近律幅值，引入tanh函数：

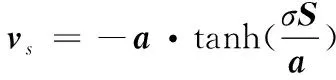
为使控制律在最大容许幅值内，考虑控制律形式，根据等效控制律给出参数取值如下：

2-1=(2-1)-(= 1,2,3)

2=(2)-(= 1,2,3)

(13)

此时本文提出的控制律可由式(5)～(13)表示。

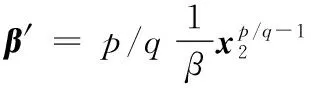
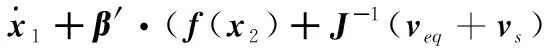
(14)

代入等效控制律式(10)得：

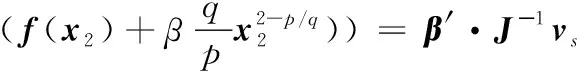
(15)

为证明本文提出的控制律可以使系统状态和在有限时间内收敛，首先介绍以下定义及引理。其中定义1给出了系统有限时间稳定的定义，引理1给出了系统有限时间稳定与Lyapunov函数之间的关系。

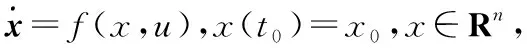
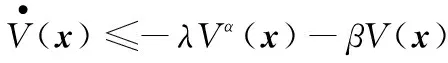
(16)

结合定义1及引理1，基于Lyapunov理论证明以下定理。

1对于系统式(4)，利用式(5)—式(13)所示的控制律，在当>>时可使系统状态和在有限时间内收敛到零。

设计Lyapunov函数为

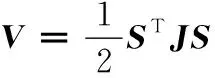
(17)

对其求导并代入切换函数导数式(26)得：

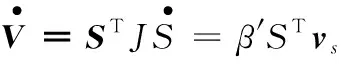
(18)

代入趋近律得：

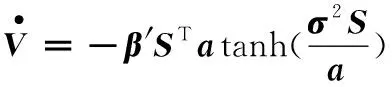
(19)

(20)

由tanh()<1得：

(21)

由≤(12)max‖‖知：

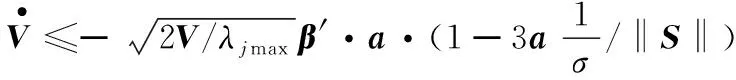
(22)

其中max为的最大特征值。令=3/σ，当‖‖>时，有

(23)

由定理1知本文提出的控制律可以使系统状态和在有限时间内收敛。

3.2 鲁棒控制重分配算法设计

对于过驱动系统，其控制器分为控制律和分配算法两级，其中控制律在上一节给出。本节为在考虑执行器输出控制力矩不确定性和推力下降故障的基础上最小化系统总推进剂消耗，设计一种鲁棒控制重分配算法，并给出一种基于线性规划的求解方法。

321 算法设计

对于直接力组合系统，其通过喷管开闭实现姿态控制，为将喷管开启时间与控制律匹配，设立一控制周期，则控制律在该周期内产生的虚拟冲量为T。因此，分配算法的目标即求解喷管开启时间，使直接力组合在控制周期产生的实际冲量与虚拟冲量为T相等。但由于控制力矩矩阵中存在未知项Δ且执行器会发生故障导致输出控制力矩下降，因此实际上=T的等式约束难以满足。为此，借鉴文献[21]，给出一种鲁棒控制重分配算法，即求解min-max优化问题如下：

(24)

‖(+Δ)-T‖≤‖-T‖+

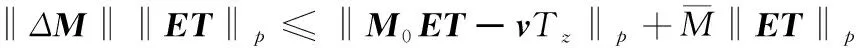
(25)

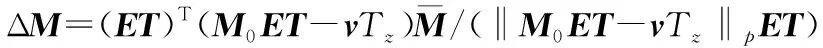
将其代入原优化问题得：

(‖-T‖)}

(26)

322 问题求解

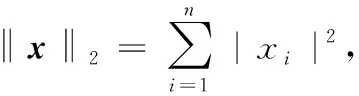
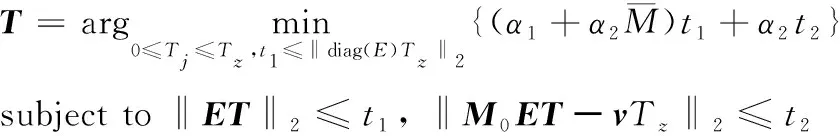
(27)

变量约束为0≤≤，≤‖diag()‖。该问题可用内点法求解。

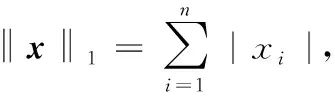
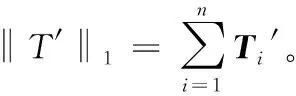
首先给出线性规划问题为

=

subject to 0≤≤,=

(28)

定义函数

令=′-T，则=()，=(-)，因此

=-, 0≤, 0≤

(30)

在=1时将问题(8)转化为线性规划问题如下：

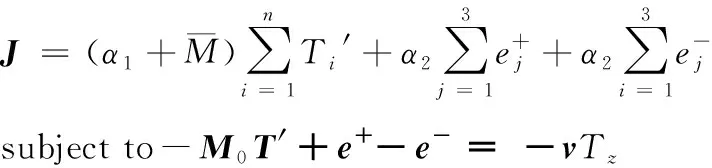
(31)

3对于min-max问题(26)，文献[21]将2范数作为目标函数形式并转化为SOCP求解，本文将1范数作为目标函数形式并转化为线性规划问题求解。两者优化目标相同，但目标函数形式不同，因此其优化结果可能存在一定差异。

4 仿真验证

为验证本文提出方法的有效性，本节针对第2节介绍的RCS，在8号喷管和10号喷管在起控0.3 s后发生推力下降故障，下降程度均为30%的工况下对本文提出的方法进行仿真验证。除此之外，为验证本文所提出方法的必要性与优越性，首先利用控制律未限幅的方法，其次利用文献[21]中方法对该工况进行仿真分析。

RCS每个喷管输出的控制力较标称值可能有最大5%的偏差，因此假设每个喷管输出力偏差为一满足正态分布的随机数，在-5%～5%之间。

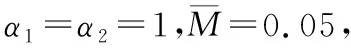
仿真结果如图2所示。其中力矩图中虚线为控制律，实线为实际控制力矩。

从图2(a)可以看出，本文提出的方法可以在系统姿态角故障情况下使其在4.5 s内收敛到0.04°，达到较好的容错控制性能，同时，从图2(b)可以看出，系统实际输出力矩由于控制力矩不确定有一定抖动，但由于分配算法具有鲁棒性，因此不确定性未对系统稳定控制造成影响。

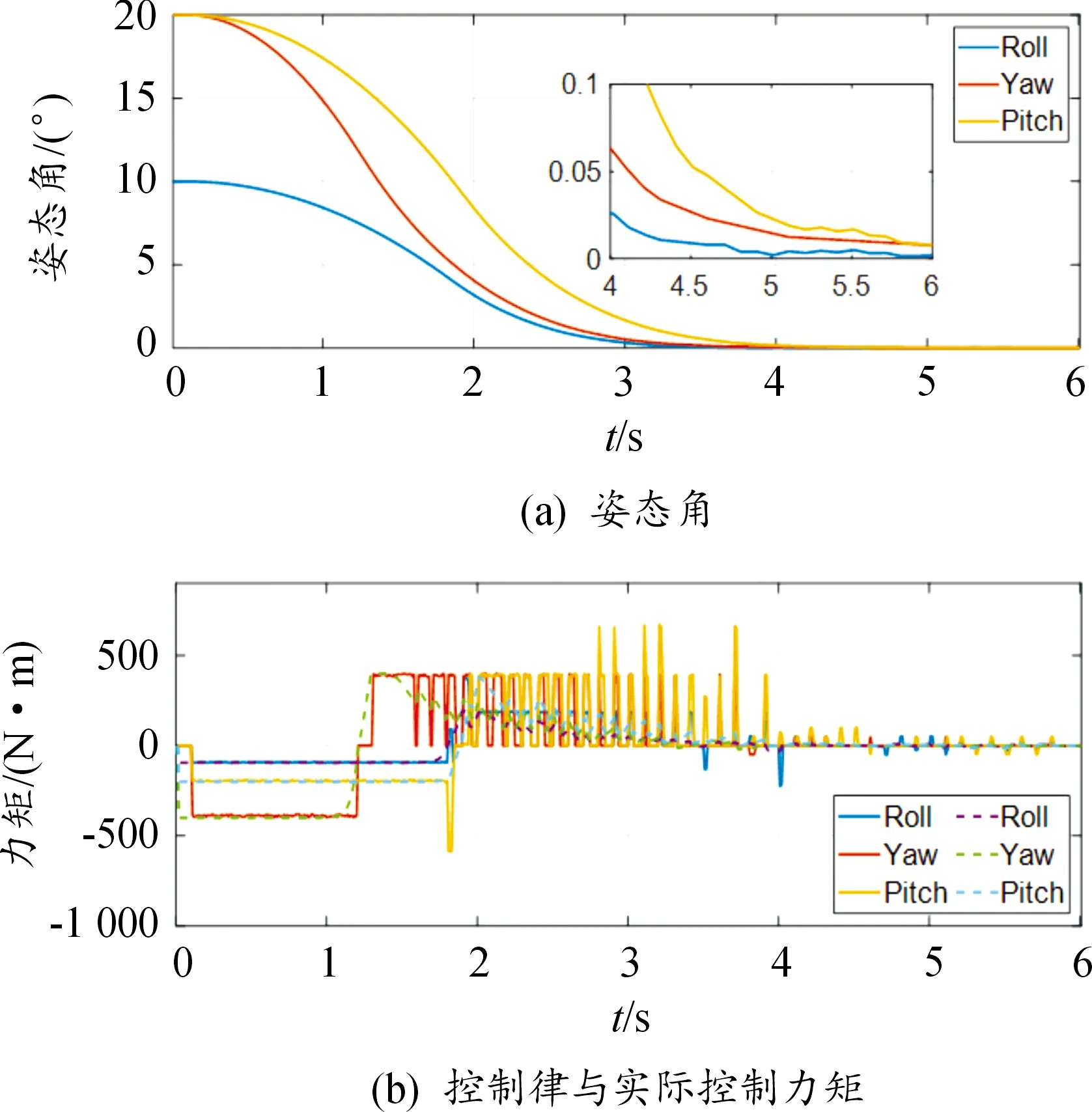
图2 本文提出方法的仿真结果曲线Fig.2 The method proposed in this paper

为验证本文提出的限幅FTC的必要性，将其与控制律未限幅的方法的仿真结果作图，有关曲线如图3。

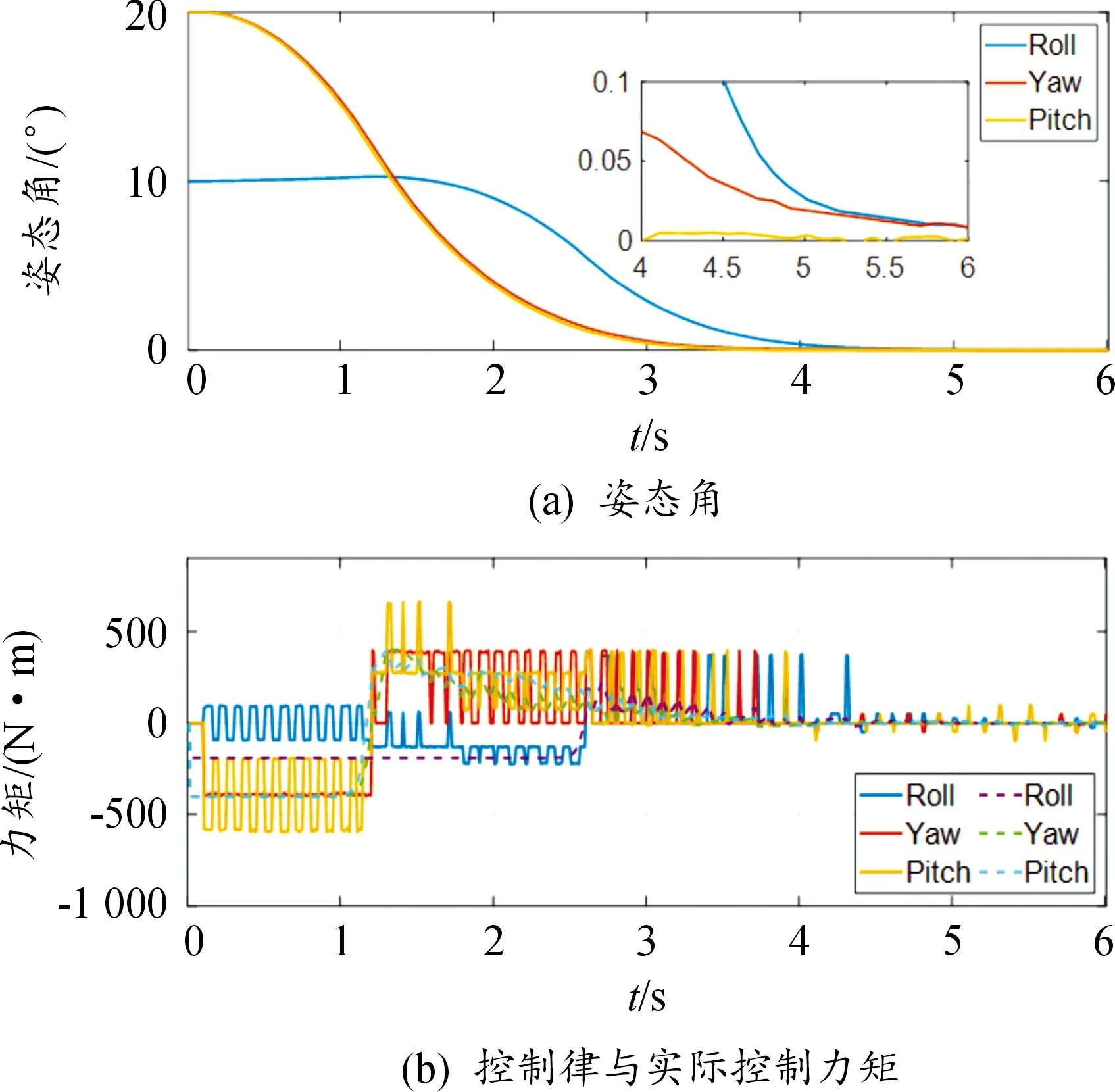
图3 控制律未限幅方法的仿真结果曲线Fig.3 The method with unsaturated control law

对比图2(a)与图3(a)可以看出，控制律未限幅情况下，控制律超出故障后系统控制能力，系统姿态角在4.5 s时收敛到0.1°，相比控制律重构情况下容错控制性能较差。

下面对比分析将鲁棒控制重分配问题转化为线性规划问题的方法，即本文提出的方法，与将其转化为SOCP的方法，即文献[21]中方法。仿真结果如图4及表2所示。

对比图4(a)与图2(a)可以看出，利用文献[21]中方法与利用本文提出的方法，系统姿态角收敛速度及控制精度相近，均在4.5 s内收敛到0.04°。从表2可以看出，利用2种方法得到的推进剂消耗量存在43 N·m的差异，为利用文献[21]中方法得到的推进剂消耗量的4.38%，优化结果相差不大。但比较二者仿真时间可以看出，利用本文提出的方法，计算时间由8.755 5 s缩短到0.373 4 s，相比文献[21]中方法缩短了95.7%，求解速度得到了较明显的提升。

图4 文献[21]的仿真结果曲线Fig.4 The method proposed in reference[21]

表2 仿真时间Table 2 The simulation time comparison

综合以上结果可以看出，本文提出的限幅有限时间FTC可以使系统在故障下实现有限时间稳定。本文给出的控制重分配方法可以在控制力矩不确定和故障情况下实现系统稳定控制，提出的求解方法可以减小计算时间。

5 结论

针对RCS执行器推力下降故障，提出了一种基于滑模和控制重分配的容错控制方法。仿真结果表明：

1) 所设计的终端非奇异滑模容错控制律可有效容忍故障，在执行器故障下仍使系统姿态角在4.5 s内收敛到0.04°。

2) 设计的鲁棒控制重分配方法能有效实现对控制力矩不确定性的鲁棒，且能根据故障信息重分配控制器控制力矩。将其转化为线性规划问题，能有效缩短求解时间，相比将其转化为SOCP的求解时间缩短了95.7%。