不同规范中抗浮锚杆计算方法对比分析

罗益斌 陈继彬 王媛媛 沈攀 魏建贵

[摘  要]：目前抗浮锚杆设计规范较多，由于各规范采用设计理论不同，计算结果相差较大，未形成共识，给工程设计带来了极大不便。文章对比6部现行规范中关于抗浮锚杆的设计计算理论和方法，得出不同规范关于抗浮锚杆设计的异同，并验证采用JGJ 476-2019《建筑工程抗浮技术标准》设计经济合理、安全可靠。进一步结合工程实际验证采用，为设计采用规范对工程抗浮设计提供借鉴。

[关键词]：抗浮锚杆; 计算方法; 锚固长度; 设计理论

TU 46A

锚杆是一种埋入岩土体的受拉杆件，承受由土压力、水压力或其他荷载所产生的拉力。锚杆用于抵抗地下水浮力时，通常称之为抗浮描杆，其锚固机理是通过与锚侧岩土层的摩阻力来提供抗拔力。抗浮锚杆适应性较好，单向受力，布置灵活。

目前行业中有关锚杆的规范较多，主要包括CCECS22：2005《岩土锚杆（索）技术规程》[1]、GB 50086-2015《岩土锚杆与喷射混凝土支护工程技术规范》[2]、GB 50330-2013《建筑边坡工程技术规范》[3]、YB/T 4659-2018《抗浮锚杆技术规程》[4]、DBJ51T102-2018《四川省建筑地下结构抗浮锚杆技术标准》[5]、JGJ476-2019《建筑工程抗浮技术标准》[6]。且各规范设计理论方法区别较大，设计时如何选取至关重要。学者在现场试验、理论分析和数值模拟等手段展开过系列的对比分析，对比分析了适用重庆地区[7]、滨海地区[8]等地的不同规范关于锚杆验收试验的相关规定，归纳总结锚杆抗拔承载力的计算方法以及安全系数的取值;并对压力分散型锚杆[9]、玻璃纤维增强聚合物锚杆[10]、全长黏结GFRP锚杆[11]等新型抗浮锚杆的蠕变特性和承载能力进行了研究。但是目前抗浮锚杆设计规范较多，由于各规范采用设计理论不同，计算结果相差较大，未形成共识。

本文对比6部现行规范中关于抗浮锚杆的设计计算理论和方法，得出不同规范关于抗浮锚杆设计的异同;进一步结合工程实际验证采用，为设计采用规范对工程抗浮设计提供借鉴。

1 锚杆设计理论

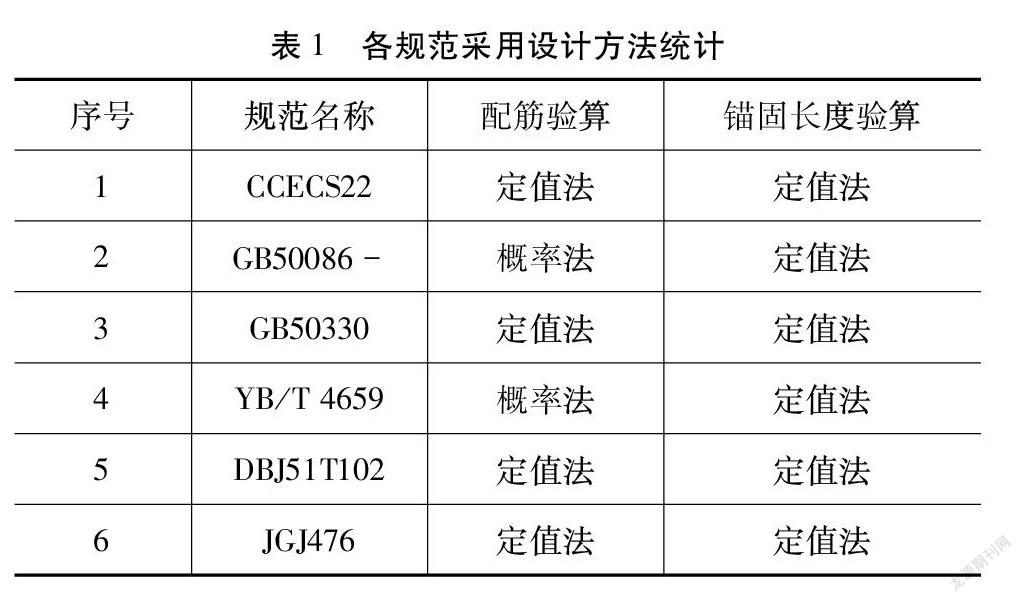
目前设计方法主要为定值法和概率法，在工程设计中，认为基本变量具有随机性，以失效概率来度量结构可靠性的方法称为概率设计法。与之相反，认为基本变量是确定的，采用以经验为主的安全系数来保证结构可靠性的方法为定值设计法。岩土工程的传统设计方法，是建立在经验基础上的定值法，随着设计理论和设计方法的进步，有逐步转向以概率为基础的极限状态法的趋势，但由于目前不够成熟，各规范两种设计方法均有采用。现对抗浮锚杆设计涉及的各规范采用设计方法进行统计如表1所示。

CCECS22：2005《岩土锚杆（索）技术规程》[1]配筋验算采用定值法中的单一安全系数法，锚固长度验算采用定值法中的单一安全系数法，针对于永久性抗浮锚杆根据安全等级不同安全系数分别为2.2、2.0、2.0。但两者作用效应均采用安全系数的同时增加了分项系数，由标准值转换为设计值，是把安全系数与分项系数混合使用，设计概念比较混乱。

GB 50086-2015《岩土锚杆与喷射混凝土支护工程技术规范》[2]配筋验算采用的是概率法中分项系数法，锚固长度验算采用定值法中的单一安全系数法。但是作用效应采用安全系数的同时增加了分项系数，由标准值转换为设计值，是把安全系数与分项系数混合使用，设计概念比较混乱。

GB 50330-2013《建筑边坡工程技术规范》[3]配筋验算采用定值法中的单一安全系数法，但是材料抗力采用设计值，安全系数只负责荷载的不确定性，材料抗力采用分项系数由标准值转换为设计值，可以看做为介于定值设计法与概率设计法之间的半概率设计法，材料抗力采用分项系数由标准值转换为设计值相当于增大了安全系数。锚固长度验算采用定值法中的单一安全系数法。

YB/T 4659-2018《抗浮锚杆技术规程》[4]配筋验算采用的是概率法中分项系数法，锚固长度验算采用定值法中的单一安全系数法。

DBJ51T102-2018《四川省建筑地下结构抗浮锚杆技术标准》[5]、JGJ 476-2019《建筑工程抗浮技术标准》[6]相同，设计理论一致，仅安全系数取值不同。

2 设计理论分析

概率法是基于可靠度理论，是将荷载与抗力都当成随机变量，那么失效或破坏也就是随机事件，将荷载与抗力的不确定性分别考虑的，影响结构安全性的有关参数，如荷载、材料强度、几何尺寸、计算精度等都采用随机变量或随机过程的概率模型来作精确的概率分析，直接采用结构的失效概率来度量结构的安全性。

定值法中的单一安全系数法，他是将工程中涉及的一切不确定性因素，都放入到唯一的安全系数之中，安全系数的取值往往是根据以往的工程经验。不确定性包括作用（荷载）的参数、材料的性质、计算的精度、施工的精确性与可靠性，同时还包括了政治、经济、环境和社会的各种条件与要求。可以说安全系数是个筐，一切不确定性因素都往里装。因而就无需再引入其他系数了，例如重要性系数、工作条件系数、折减系数等[12]。

当基本变量的变异性小、计算模型准确，概率设计和定值设计的结果可达到统一;当基本变量变异性大、计算模型不准确，2种方法很难统一。一般认为对于材料性能稳定、变异性小、计算模型准确、统计资料齐全的结构设计采用概率设计;对于材料性能变异较大、计算模型不准确、缺乏统计资料的岩土类设计采用定值法设计。《建筑工程可靠性设计统一标准》规定“建筑结构设计宜采用以概率理论为基础，以分项系数表达的极限状态设计方法;当缺乏统计资料时，建筑结构设计可根据可靠的工程经验或必要的试验研究进行，也可采用容许应力或单一安全系数等经验方法进行”。

所以在岩土工程，凡与岩与土有关的设计，一般均用安全系数法;而只涉及到钢材、混凝土与砂浆等材料时则采用概率法。因此锚杆锚固长度验算岩土设计普遍认为采用定值法设计较为合理，这一点岩土工程師已形成共识。但是针对锚杆配筋验算则有不同理解。主要分歧是部分工程师认为配筋验算，主要涉及钢材、混凝土与砂浆等材料，此类材料性能稳定、变异性小、计算模型准确、统计资料齐全应采用概率设计，但是往往忽略了抗浮锚杆与岩土界面的影响，同时施工过程锚杆一般直径较小，施工的精确性与可靠性很难保证，施工过程中无法避免的垮孔、缩颈、漏浆、注浆不到位等施工缺陷，均严重影响锚杆配筋的的发挥和耐久性。因此采用定值法设计抗浮锚杆更为合理，采用安全系数法将工程中包含的一切不确定性因素，都放入安全系数之中。根据以往的经验确定安全系数，保证工程安全运行。

3 不同规范对比

目前各规范采用设计理论不尽相同无法简单的评价各规范经济可靠性，上文分析锚杆设计建议采用单一安全系数法进行设计，因此对各规范设计方法转换为单一安全系数（概率法及设计分项系数均均进行转换合并，总称为安全系数）进行对比。

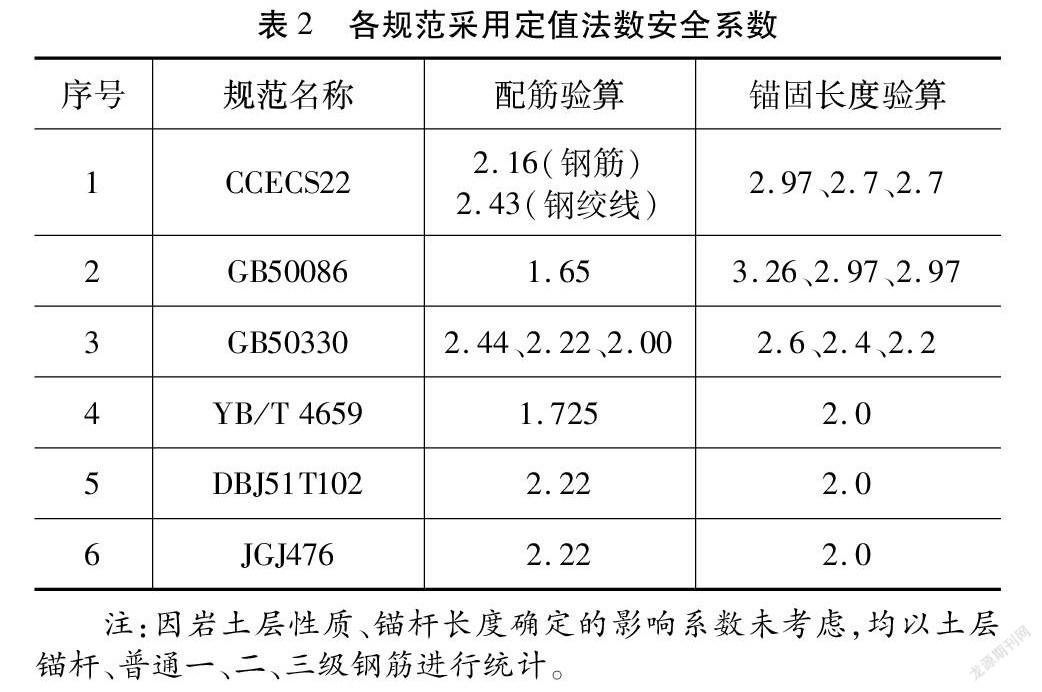
由于錨杆锚固长度主要以锚固体与岩土层锚固长度控制，因此主要以配筋验算和锚固体与岩土层锚固长度验算对各规范进行对比。转变后统计如表2所示。

此时各规范比较可简单的看作为安全系数的比较，安全系数越低则经济性越好，但能否满足可靠性和耐久性要求则需要实际工程进行验证。

4 工程案例

以成都某工程为例，该工程抗浮设计水位绝对高程为516.00 m。场地基底岩土主要为：

松散卵石（Q4al+pl）： 灰黄色、灰色，松散，饱和，卵石粒径一般2～5 cm，含量50%～55%。卵石骨架间被砂、少量圆砾充填。该层呈层状分布。N120超重型动力触探修正击数为2～4击。

稍密卵石（Q4al+pl）：灰黄色、灰色，稍密，饱和，卵石粒径2～8 cm，卵石含量55%～60%左右，卵石骨架间被砂、少量圆砾充填。该层呈层状分布。N120超重型动力触探修正击数4～7击。

中密卵石（Q4al+pl）：灰黄色、灰色，中密，饱和，卵石粒径2～8 cm，卵石含量60%～65%，卵石骨架间被砂、少量圆砾充填。该层呈层状分布。N120动力触探修正击数7～10击。

密实卵石（Q4al+pl）：灰黄—黄褐色，密实，饱和，卵石粒径一般4～10 cm，个别大于20 cm。以层状分布，卵石含量约70%～80%，卵石骨架间被砂、少量圆砾充填。层位稳定，N120修正后的平均击数为12.4击。本次勘察未揭穿。

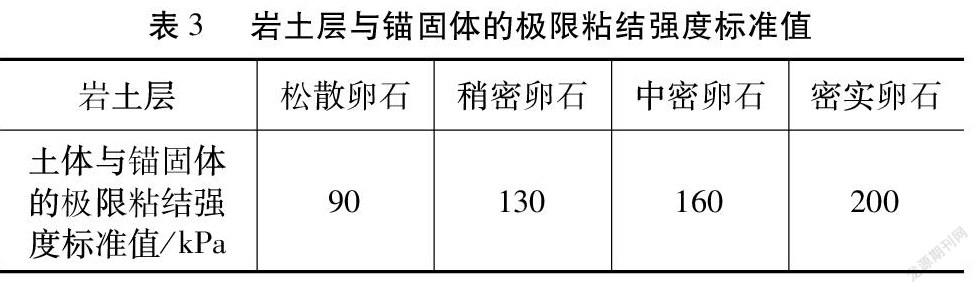
岩土层与锚固体的极限粘结强度标准值如表3所示。

本工程地下室底板下局部区域设抗浮锚杆，单根锚杆轴向拉力标准值为230 kN，基底以下场地为松散卵石、稍密卵石、中密卵石、密实卵石，标准值综合取值根据工程经验及抗浮锚杆区域地层加权平均值为123.0 kPa。

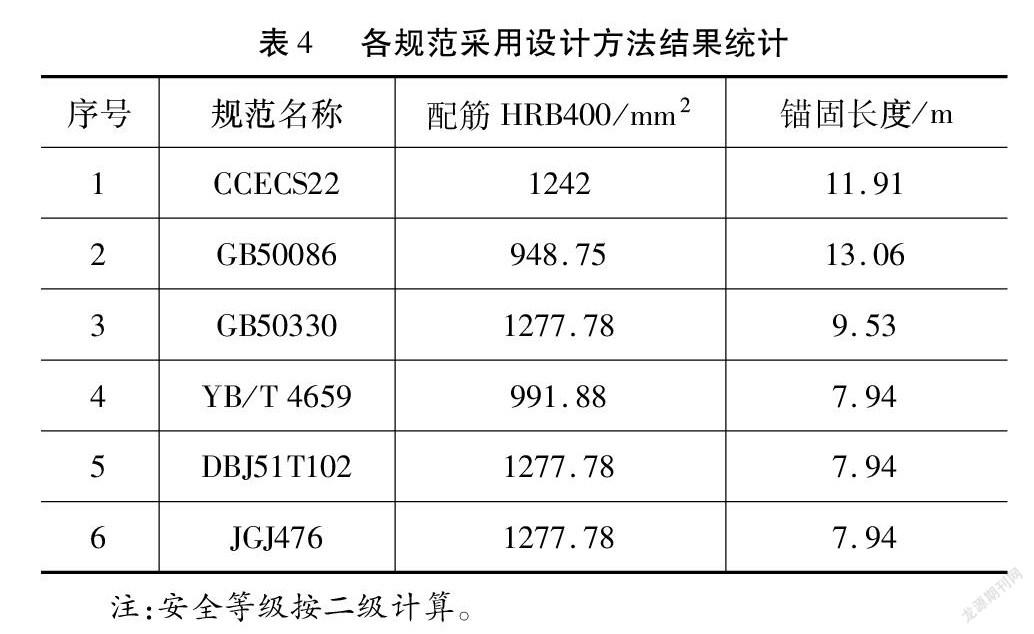
分别按不同规范进行设计，结果统计见表4。

本工程按JGJ 476-2019《建筑工程抗浮技术标准》设计，实际配筋采用3根25 mm的HRB400螺纹钢筋作为锚杆配筋，As=1 473 mm2，锚杆长度增加0.5 m的结构要求，实际施工按锚杆锚固长度不小于8.5 m，经检测抗拔承载力大于设计轴向拉力标准值为230 kN。

5 结论

目前抗浮锚杆设计规范较多，由于各规范采用设计理论不同，计算结果相差较大，未形成共识，本文通过各规范对比及工程实际验证采用《建筑工程抗浮技术标准》设计经济合理、安全可靠，因此推荐采用JGJ476-2019《建筑工程抗浮技术标准》进行抗浮锚杆设计。

参考文献

[1] 岩土锚杆（索）技术规程： CCECS22：2005[S].

[2] 岩土锚杆与喷射混凝土支护工程技术规范： GB50086-2015[S].

[3] 建筑边坡工程技术规范： GB50330-2013[S].

[4] 抗浮锚杆技术规程： YB/T 4659-2018[S].

[5] 四川省建筑地下结构抗浮锚杆技术标准： DBJ51T102-2018[S].

[6] 建筑工程抗浮技术标准： JGJ476-2019[S].

[7] 林亮伦，杜清超等. 重庆地区不同规范中锚杆验收试验对比分析[J]. 重庆建筑.2018（7）：59-62.

[8] 贾金青，宋二祥. 滨海大型地下工程抗浮锚杆的设计与试验研究[J]. 岩土工程学报.2002（6）： 769-771.

[9] 张孟玫， 衡朝阳， 周智. 无粘结压力分散型锚杆的锁定荷载计算[J]. 建筑科学， 2020， 36（7）：26-32.

[10] 郑晨， 白晓宇， 张明义，等. 玻璃纤维增强聚合物锚杆在地下结构抗浮工程中的研究进展[J].材料导报. 2020， 34（13）： 13194-13202.

[11] 白晓宇，张明义等. 全长黏结GFRP抗浮锚杆拉拔特性分析[J]. 中南大学学报：自然科学版.2019（8）：1991-2000.

[12] 李广信.关于《建筑边坡工程技术规范GB 50330—2013》的讨论[J].岩土工程学报，2016，38（12）：2322-2326.