复杂气象环境海上无线通信信道衰落估计模型

2022-07-09戴亚盛马柏林乐光学

电信科学 2022年3期

戴亚盛，马柏林，乐光学

戴亚盛1,2，马柏林1，乐光学1

（1. 嘉兴学院信息科学与工程学院，浙江嘉兴 314001；2. 上海大学计算机工程与科学学院，上海 200444）

海洋表面受电磁波稀疏散射、海浪阴影衰落、舰船摆动、晴雾雨雪等复杂环境因素影响，海上无线通信信道衰落建模极其复杂。通过分析直射、镜面反射、漫反射和复杂气象环境对信道衰落的影响，提出了复杂气象环境海上无线通信信道衰落估计模型。设计改进蜂群算法对该信道衰落估计模型求解，构建以sin(·)函数为算子引导跟随蜂进行搜索，降低搜索空间，提高求解效率和精度。引领蜂以概率接收侦查蜂解进行更新，抑制求解算法陷入局部最优的问题。实验结果表明，提出的模型与波动双射线模型和地球曲率模型相比，精度平均提升13.58%和11.43%；与布谷鸟搜索、遗传算法、模拟退火算法等对比分析，搜索时间分别减少60.48%、45.18%、43.23%。

海洋环境；无线通信；蜂群算法；信道衰落

0 引言

海上无线通信信道衰落受海浪阴影效应、发射机接收机相对运动、海洋表面电磁波稀疏散射、海上气象环境损耗等诸多复杂因素影响，具有稀疏性、多径不稳定性、气象环境影响大等区别于陆地通信信道独特特性，传统基于陆地城市环境构建的瑞利、高斯分布通信信道衰落模型不能有效表征其变化[1]。海上无线通信信道衰落模型是研究海上无线通信信道精确辨识、估计、均衡、解调和解码，在接收端准确恢复发射信息，实现端到端的联合优化的基础工作，因此，对于海上无线通信系统研究具有重要意义[2-3]。海上无线通信信道衰落建模已成为突破海上无线通信信道研究的关键，是产业界关注的重点问题之一。

为有效构建海上无线通信信道衰落模型，本文提出一种复杂气象环境下海上无线通信信道衰落估计模型（estimation of wireless channel fading model in maritime communication for complex meteorological environment，EWCFM-CME）。本文通过分析晴、雾、雨、雪和雨雪混合复杂气象环境对海上无线通信信道衰落影响，融合直射、镜面反射和漫反射路径无线通信信道衰落模型，构建复杂气象环境下海上无线通信信道衰落估计模型，设计改进蜂群算法对海上无线通信信道衰落估计求解。在衰落参数值域随机生成个初始蜂群，以引领蜂为中心，通过构建以sin(·)函数为算子引导跟随蜂进行搜索，降低搜索空间，提高求解效率和精度。运用贪婪策略选择个适应度最优的跟随蜂，由侦查蜂标记构建侦查蜂集。以侦查蜂解集的均方差判断其解的准确度，避免因求解误差导致的算法抖动。引领蜂以概率接收侦查蜂解，将该侦查蜂更新为新的引领蜂，抑制引领蜂更新时容易陷入局部最优的问题。基于舟山海域气象数据，模拟四季不同海况环境以仿真分析EWCFM-CME性能。

1 相关研究

文献[1]提出一种综合考虑反射、阴影、发散和绕射等因素的路径损耗模型。在挪威离岸距离为45 km的平静、寒冷的公海上进行频率为2 GHz的信道衰落测量实验验证，结果表明其均方根误差较小。文献[4]分析海上大气折射、海浪运动、海水表面散射、发射机/接收机相对运动、海上气象环境损耗等对海上无线通信信道的影响，综述了海上无线通信信道建模方法，指出稀疏性和位置依赖性是海上无线信道建模重要特性。文献[5]提出一种具有随机相位的镜面反射和漫反射两个分量构成的波动双射线（fluctuating two-ray，FTR）模型，频率为28 GHz的室外信道实测结果表明，FTR模型能够有效拟合不同的衰落分布。文献[6]通过在码头和海岸巡逻艇的窄带信道测量系统，研究实测2.4 GHz频段的大尺度和小尺度衰落特性，指出在大尺度衰落上，考虑海浪高度的双射线模型能够较好地拟合实测数据集，对于小尺度衰落，分析了莱斯（Rician）、Nakagami、瑞利（Rayleigh）分布的适用性和精度。文献[7]通过在海上进行VHF/UHF（very high frequency/ultra high frequency）频段的一系列通信信道试验，分析指出华为海上传播模型、双射线模型、远距离莱斯模型分别适用于视距路径、临界视距路径和超视距路径传播损耗。文献[8]提出一种船舶在内海水道航行的半确定性的路径损失模型。该模型结合国际电信联盟的经验路径损耗模型和几何计算方案，建模反射和附近建筑的绕射路径，通过与信道测量数据的比较，验证了该模型的有效性。文献[9]提出了一种基于-分布的离群值鲁棒三分位参数估计方法，通过利用模拟数据和实测数据对三分位估计器进行了评估，结果表明，该估计器对原始海杂波数据中的异常值具有较强的鲁棒性。文献[10]在中国黄海海域进行了信道测试，根据海况参数和接收信号的功率时延谱等特征判断实验环境下海上蒸发波导的存在性；提出潮汐因子修正的两径时变信道模型，并验证信道小尺度衰落符合莱斯分布。文献[11]研究海浪对无线电传播和通信链路质量的影响，通过建模海浪波动模型和信道衰弱，推导直射通信的条件，并仿真评估其模型中海浪参数与信道衰落的相关性。

文献[12]针对高速信道的双选衰落和非平稳特性，提出一种基于基扩展模型（basis expansion model，BEM）的贝叶斯滤波的信道估计方法，仿真分析表明，所提方法有效提升了估计精度性能。文献[13]提出一种非平稳性快速时变通信信道建模仿真方法，通过引入积分项和随机偏移，有效复现时变散射的非平稳信道且保证了散射支路的独立性。数值仿真结果表明，改进方法模拟信道的概率密度函数、自相关函数和多普勒功率谱密度与理论值吻合良好。文献[14]通过数值积分方程构建热带气候地面微波通信链路雨衰预测模型，并在频率为15 GHz的信道环境中进行仿真测试，结果表明能够比国际电信联盟无线电通信局（International Telecommunication Union-Radio Communications Sector，ITU-R）标准模型和经典雨衰预测模型更准确。文献[15]研究了降雪环境下频率为2.425 GHz的通信路径损耗，提出了一种经验路径损耗模型，并在不同降雪强度的环境中验证了其准确性。文献[16]研究港口环境下信道慢衰落和快衰落效应的分布模型，以频率、基站天线高度等为约束参数，建模信道多元线性回归估计问题，通过实测结果发现对数正态分布可以拟合慢衰弱，Nakagami分布可以有效拟合快衰落。文献[17]对无人机−舰船的空−海6G信道进行了研究，推导研究其时−空自相关函数、多普勒功率谱密度、时延、角度、平稳间隔和均方根延迟扩展等特征，基于实测数据的比较，验证了所提出的信道模型的准确性。文献[18]研究了莱斯衰落信道，镜面反射、散射分量的发射/接收波束信道状态信息（channel state information，CSI）形成情况。在多输入多输出（multipleinput multipleoutput，MIMO）系统测试结果发现，当两个天线数相乘而减小时，遍历最高速率保持不变，同时提高了估计的精确度。文献[19]提出了一种浅海信道弹性结构声辐射快速预报的联合波叠加法，该方法结合了浅海信道传输函数、多物理场耦合数值计算法和波叠加法理论，可快速预报浅海信道下弹性结构辐射场。文献[20]提出快速贝叶斯匹配海上通信信道估计算法，通过基于奇异值分解信道矩阵，估计稀疏信道，有效提高了信道估计准确性。

海洋无线通信信道衰落相关文献检索结果发现，现有研究均针对特定的海洋环境进行建模和衰落参数估计，其结果适用于其实验仿真环境且效果显著，但海洋环境复杂，不同的地理位置和气象环境均会影响海上无线信道衰落，导致现有模型精度不高，不能普遍适用。综合考虑海洋复杂气象环境对无线通信多径信道衰落估计模型及如何高效准确求解研究较少。基于数据驱动模式，综合分析海上通信信道稀疏路径损耗、海洋表面电磁波散射、海浪阴影衰落、雨雪雾等复杂海况气象环境对海上无线通信信道衰落的影响，构建复杂气象环境下海上无线通信信道衰落估计模型。基于舟山海域气象数据，模拟四季不同海况环境下仿真分析EWCFM- CME模型的精度和适应性。

2 海上无线通信信道衰落建模

图1 海上无线信道衰落建模

2.1 海上无线通信信道模型

根据文献[5-10]对海上无线信道实测数据分析研究，在发射机到接收机的海上无线多径信道中，直射、镜面反射和漫反射路径传输的信号能够与噪声相互独立。假设发射波为()，在时刻，构建海上无线通信信道合成波()为：

其中，DP、SR、DR分别为直射路径、镜面反射路径和漫反射路径的幅值，DP、SR、DR分别为其到达时延，(σ)为复合高斯分布函数。根据通信原理，对于任一路径信号到幅值与衰落关系如式（2）所示[16]。

其中，()为发送信号的调制幅值，为信道时延，是电磁波传播距离，PL()为信道衰落模型。PL()衰落模型需要根据直射、镜面反射和漫反射路径信道的变化性质和特征构建。

2.2 海上无线通信信道衰落模型

海上无线通信信道大尺度衰落描述信道衰落的总体变化趋势，主要指因传输距离产生的路径损耗以及障碍物产生的阴影衰落；小尺度衰落是在小范围内的快速波动，主要由海浪、发射机与接收机相对运动产生，具有随机性。海上无线信道衰落建模如图1所示。

构建直射路径信道衰落模型表征路径损耗和阴影衰落的大尺度特征，镜面反射、漫反射路径信道衰落模型表征海洋表面反射、海浪阴影效应、发射机与接收机的相对运动特征，实现衰落估计参数解耦，提升衰落建模参数估计效率。

根据Friis公式结合信道衰落定义，在给定距离下信道衰落模型PL()表示为[21]：

其中，接收天线、发射天线增益r、t单位为dBi，工作频率单位为Hz，距离单位为m，c为光速。由于Friis公式在理想环境中测得，实际环境信道衰弱变化复杂，需要对其进行改进。

（1）直射路径信道衰落模型

考虑海上大气传输损耗，对于海上无线信道直射路径衰落建模为：

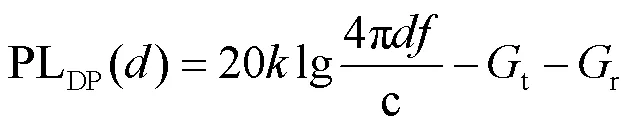
其中，为海上稀疏信道衰落因子。

（2）镜面反射路径信道衰落模型

镜面反射路径衰落建模主要考虑海上稀疏信道路径损耗、海洋表面反射损耗和浪面反射阴影衰落效应。直射路径、镜面反射路径、漫反射路径无线传播模型如图2所示。

图2 直射路径、镜面反射路径、漫反射路径无线传播模型

海洋表面反射电磁波功率满足Fresnel公式，则海洋表面反射路径损耗为：

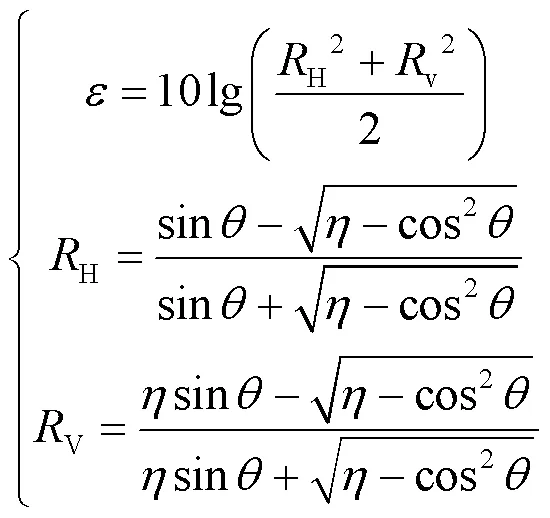
其中，H为水平极化波反射系数，V为垂直极化波的反射系数，为海水的相对介电常数，为无线电波入射角。镜面反射入射角表示为：

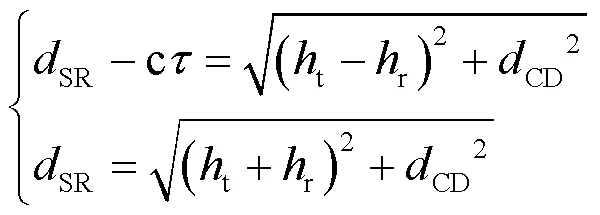
由式（7）解得：

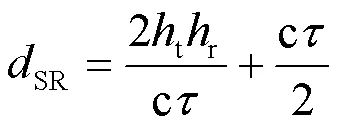
联立式（5）、式（6）、式（8），求解。

海浪运动导致镜面反射信号广域散射，形成海浪局部阴影衰落效应。这种变化产生了反射信道衰落周期性波动。设计sin2(·)函数进行拟合，PLSR()为：

其中，SR为镜面反射路径损耗系数，h为海浪高度均方根，为海浪阴影衰落指数，为衰落周期。

（3）漫反射路径信道衰落模型

根据文献[8]对漫反射路径和镜面反射路径下的测量结果，漫反射路径和镜面反射路径功率比服从高斯分布。根据该性质，构建漫反射路径衰落模型PLDR()为：

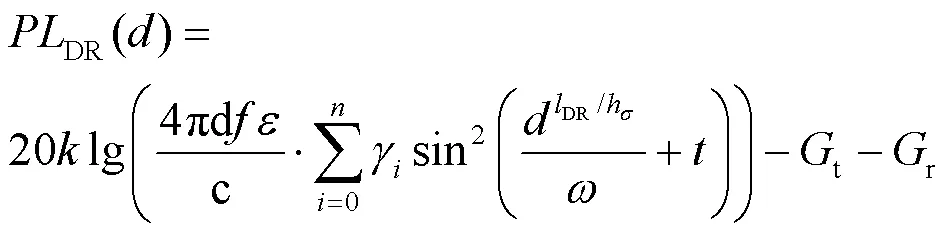
其中，服从高斯分布(,σ2)，为漫反射强度离散程度因子，DR为漫反射反射路径损耗系数。

2.3 复杂气象环境下的海上无线通信信道衰落模型

气象环境对无线信道衰落影响不可忽略。文献[14-15, 21]对晴、雾、雪和雨气象环境下的通信信道路径损耗因子进行测定，结果表明不同的气象环境具有不同的衰落特征。根据文献[21]构建不同气象环境下海上无线信道衰落模型如式（11）所示。

其中，()为不同海上气象环境衰落系数，为天气类型标识，=0、1、2、3、4分别代表当前天气为晴、雾、雨、雪、雨雪混合气象环境，构建其衰落系数模型。

根据文献[14-15, 21]得到，无线电波传播频率越高，其电波传输能量越高，越容易被海上大气、雨、雪、雾等吸收造成信号衰落，气象环境衰落与频率因子成正比；通信频段会受到太阳电磁辐射干扰，呈现昼夜周期变化；由于日光照射使得温度变高，导致更多的海水蒸发引起无线电波折射损耗，使白天衰落强度高于夜晚。海洋气象环境构建其衰落系数模型如下：

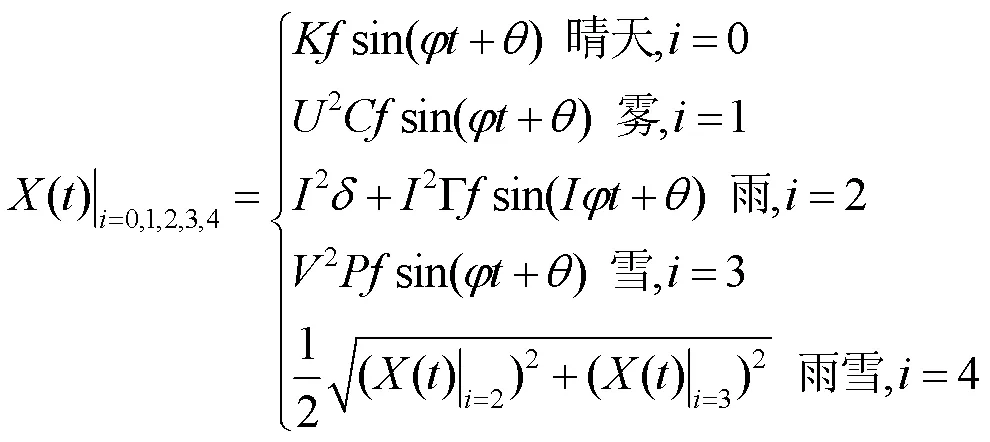
当有雨雪混合环境时，由于雨雪衰落影响并非平均，而是以其中的主要气象环境衰落影响为主导，采用其系数均方中值进行估计。

将不同气象环境下的衰落系数代入式（11）求解海上气象环境无线衰落，并融合直射、镜面反射、漫反射衰落模型，构建海上无线通信信道衰落模型为：

海上无线通信信道衰落模型仿真算法描述如下所示。

步骤1 系统初始化，设置迭代步长，根据历史当月海域气象数据创建哈希队列{}，为气象标识，Î{0, 1, 2, 3, 4}。

图3 海上无线通信信道衰落模型仿真结构

步骤2 若气象队列未满，以时间为种子，通过哈希散列函数生成映射=Hashlist(Rand())，进入气象队列；否则，重新选择。

步骤3 当随机时间触发器触发气象状态改变事件时，从气象队列获取气象状态，根据其气象环境参数代入式（12）求解()|=j，将()|=j代入式（11）、式（13）求解海上无线通信信道衰落模型。

步骤4 判断仿真测试是否结束：否，转到步骤（2）；是，输出海上无线通信信道衰落模型PL()。

3 改进蜂群算法估计海上无线通信信道衰落

3.1 问题描述

构建优化目标函为：

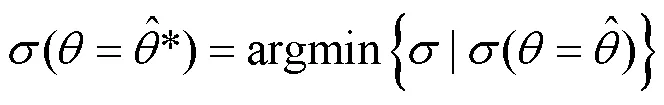
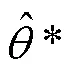
3.2 基于正弦函数算子的改进蜂群搜索求解算法设计

采用基于正弦函数算子的改进蜂群搜索算法求解海上无线通信信道衰落估计问题。蜂群搜索算法以引领蜂的解为中心，采取深度或广度优先搜索策略，以局部随机搜索或梯度搜索求解，该方法对求解参数量少、时空复杂度低的问题很有效，但不适合于复杂、规模大的多维参数优化问题求解。为提高求解效率和精度，降低搜索空间，构建以sin(·)函数为算子的迭代函数替换传统的线性迭代函数。运用贪婪策略选择个适应度最优的跟随蜂，由侦查蜂标记并入侦查蜂集，构建新的侦查蜂集。以侦查蜂解集的均方差判断其解的准确度，避免因求解误差导致的算法抖动。引领蜂以概率接收侦查蜂解，将该侦查蜂更新为新的引领蜂，抑制引领蜂更新时容易陷入局部最优的问题。

其中，0为初始引领峰距离阈值。每个引领蜂生成搜索种群，以引领蜂为中心，派出个跟随蜂搜索。跟随蜂解的生成函数如式（18）所示。

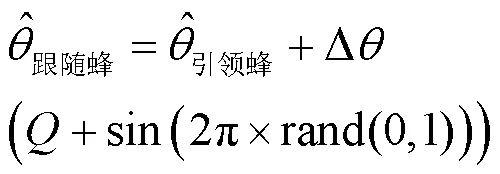
将跟随蜂解集以适应度降序排列，选择前个由侦查蜂标记，<，构建侦查蜂集为；每次迭代完成，引领蜂从侦查蜂集中以概率接收侦查蜂解，概率为：

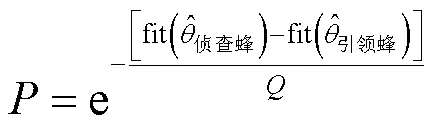
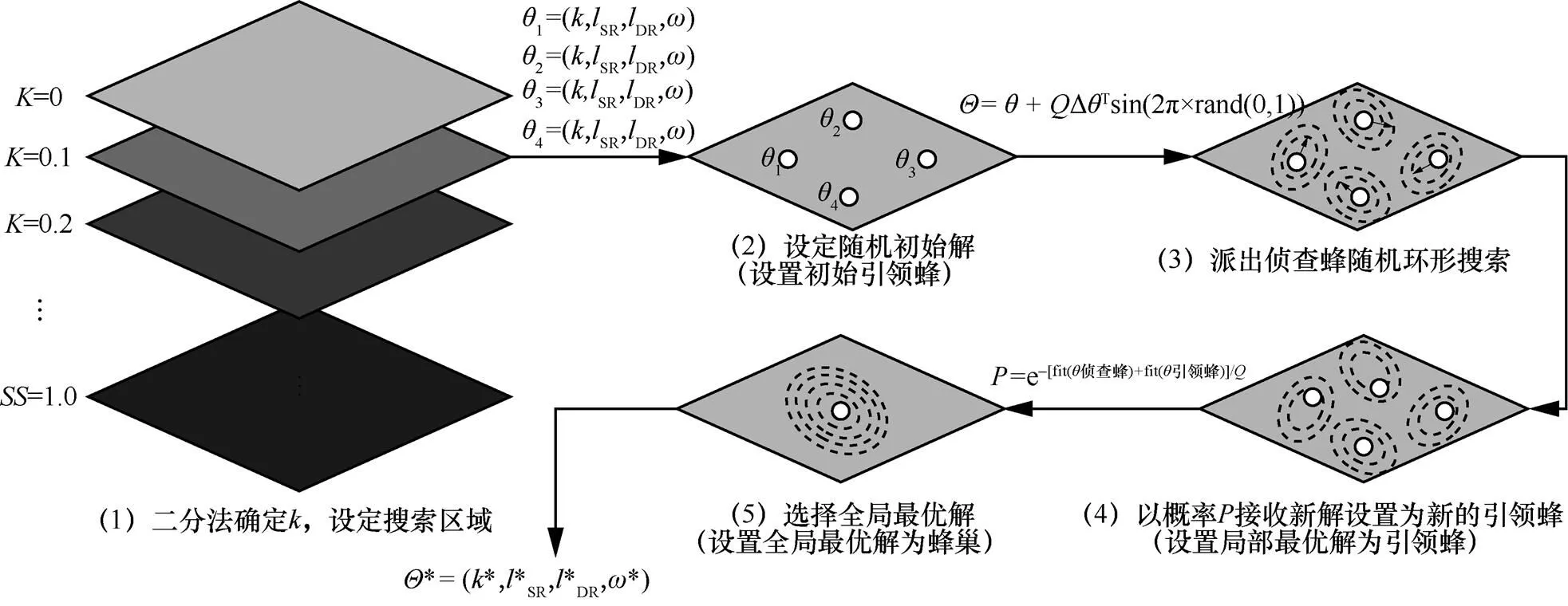
基于正弦函数算子的改进蜂群求解算法过程如图4所示。通过二分法确定参数的取值，设置蜂群搜索区域；在搜索区域中随机生成个初始蜂群，设置每个蜂群中的局部最优解为初始引领蜂位置。以引领蜂为中心，跟随蜂以式（18）进行迭代搜索发现可行解，计算可行解的适应度。运用贪婪策略选择个适应度最优的跟随蜂，由侦查蜂标记并入侦查蜂集，构建新的侦查蜂集。引领蜂分析当前侦查蜂集的状态，以式（20）概率接收侦查蜂解，将该侦查蜂更新为新的引领蜂；输出全局最优的搜索结果。

基于正弦函数算子的改进蜂群求解算法方案如下。

步骤3 初始化种群，初始化蜂群数量、参数SR/DR，的迭代增量ΔSR/ΔDR/Δ、最大迭代搜索次数、侦查蜂环形搜索最大次数max。

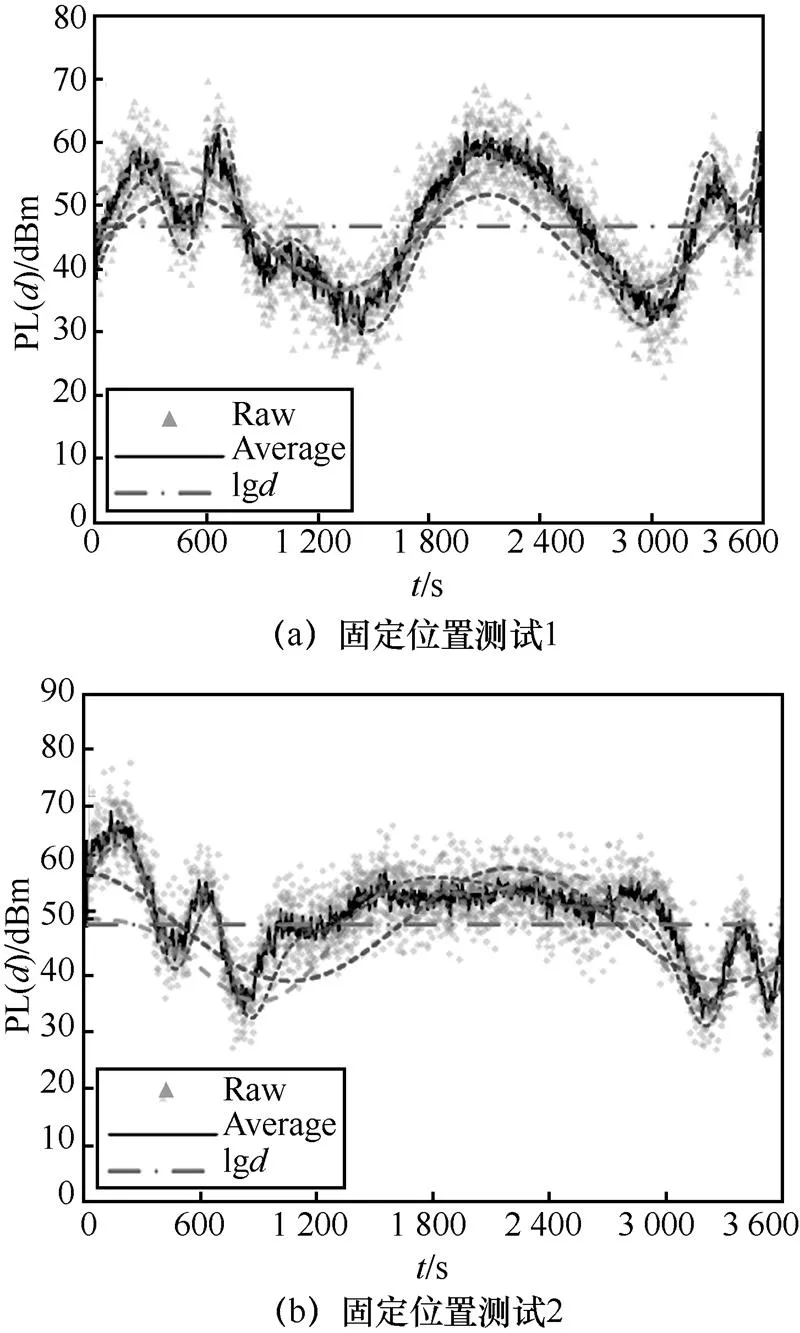
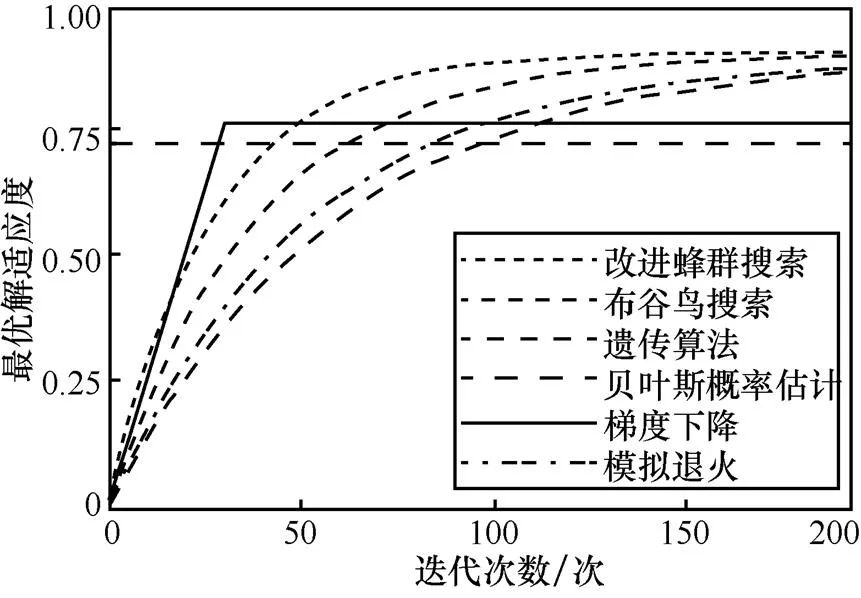
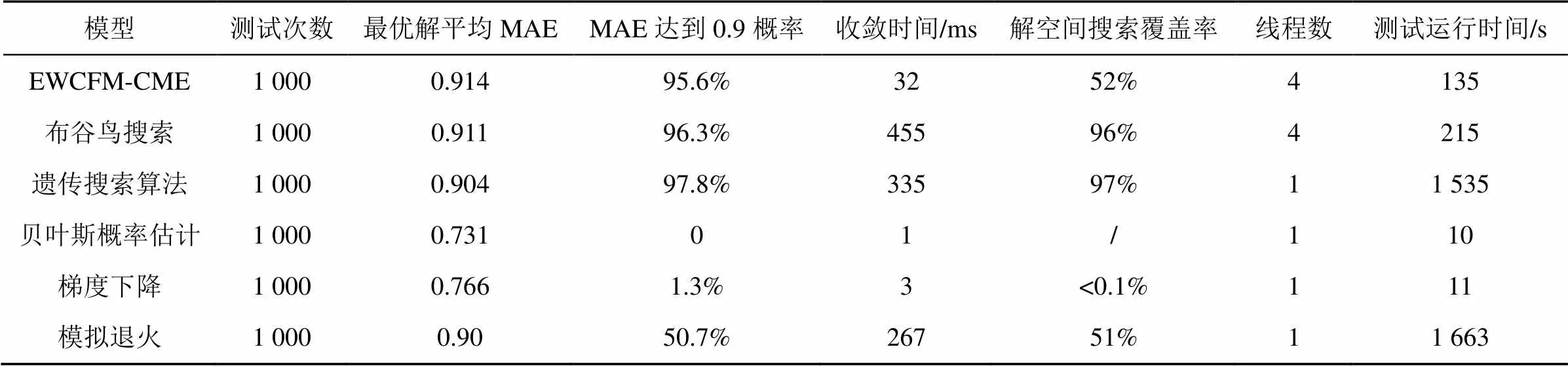
步骤5 当

以式（20）的概率接收侦查蜂的解，更新引领蜂位置，++。

图4 基于正弦函数算子的改进蜂群求解算法过程

4 实验仿真分析

4.1 实验1 海上无线通信信道衷落模型性能分析

以基站为中心，讨论舰船向基站运动、舰船离开基站运动、舰船与基站相对静止3种状态，仿真分析其海上无线通信信道衰落变化特征，以平均绝对误差（mean absolute error，MAE）、均方根误差（root mean squared error，RMSE）、迭代次数、时间开销等为评价指标，将EWCFM-CME模型与FTR模型[1]、地球曲率路径损耗（round earth loss，REL）模型[5]进行对比分析。

设海上智能通信基站为发射机，与舰船为接收端进行无线通信，舰船搭载双频无线接收机S-IR680进行无线电信号采样，包括信号的振幅、频率、相位等特征参数。基站高22.1 m，发射天线长2.7 m；舰船高11.4 m，接收天线长1.1 m；仿真实验采样包含两个阶段，海上无线通信信道衰落仿真实验状态如图5所示，共4组采样数据，海上无线通信环境仿真和数据集参数见表1。

图5 海上无线通信信道衰落仿真实验状态

舰船以11 km/h的恒定速度线性航行，实验采样分为两组，一组为向基站方向航行，另一组为离开基站方向航行。在平均气温11～26℃晴天微风平静海面环境下，通过海上智能通信基站发射固定的心跳射频信号至舰船接收进行采样，采样间隔为5 s，采样时间为5 h。

海上智能通信基站和舰船位置相对固定，舰船距离基站29 km。实验采样分为2组，分别在清晨6点气温11℃和下午1点气温26℃的晴天微风平静海面环境下，通过海上智能通信基站发射固定的心跳射频信号至舰船接收进行采样，采样间隔均为1 s，每次采样时间为1 h。

4.1.1 海上无线通信信道特征分析

舰船静止舰船与通信基站相对位置固定时，基站发射信号和舰船接收信号仿真实验结果如图6所示。

● 固定位置数据集，接收平均丢失率为12.10%，丢失信号具有时空随机性。

● 信道频率随海上环境变化而改变，这是海浪变化引起无线电信号频率变化。

● 信号强度衰减具有频率选择性和时空随机性。

表1 海上无线通信环境仿真和数据集参数

4.1.2 EWCFM-CME模型性能分析

（1）舰船相对基站移动无线通信信道衰落模型性能分析

舰船相对基站移动海上无线通信信道衰落模型如图7所示，舰船相对基站移动海上无线通信信道衰落模型性能参数见表2。

舰船相对基站移动海上无线通信信道衰落模型仿真实验结果表明如下。

● lg对数－距离路径损耗模型反映了海上无线通信信道在距离上平均衰落变化。

● 向基站方向航行时，EWCFM-CME与FTR、REL相比，MAE分别提升10.39%、15.33%，RMSE分别提升10.28%、15.15%；离开基站方向航行时，EWCFM- CME与FTR、REL相比，MAE分别提升11.79%、14.67%，RMSE分别提升11.78%、14.63%。

图6 基站发射信号和舰船接收信号仿真实验结果

图7 舰船相对基站移动海上无线通信信道衰落模型

表2 舰船相对基站移动海上无线通信信道衰落模型性能参数

● 向基站方向航行时，EWCFM-CME与FTR、REL相比，MAE>0.9即能够有效估计的距离均提升2.5倍；离开基站方向航行时，EWCFM-CME与FTR、REL相比，有效估计的距离均提升5.3倍。

● 向基站方向航行时，EWCFM-CME与FTR、REL相比，迭代次数分别减少75.35%、39.54%，算法运行时间分别减少60.48%、79.18%；离开基站方向航行时，EWCFM-CME与FTR、REL相比，迭代次数分别减少79.06%、20.56%，算法运行时间分别减少69.49%、77.35%。

（2）舰船相对基站静止海上无线通信信道衰落模型性能分析

舰船基站固定位置海上无线通信信道衰落模型如图8所示，舰船－基站固定位置海上无线通信信道衰落模型性能见表3。

图8 舰船基站固定位置海上无线通信信道衰落模型

舰船基站固定位置海上无线通信信道衰落仿真实验结果表明如下。

● 舰船位置固定时，影响海上无线信道衰落的因素主要是气象环境、海浪运动等，lg对数－距离路径损耗模型反映了由传输距离导致的基本损耗。

表3 舰船－基站固定位置海上无线通信信道衰落模型性能

● 对于固定位置海上无线通信信道衰落，EWCFM-CME与FTR、REL相比，MAE分别提升47.74%、46.22%，RMSE分别提升47.01%、45.51%；离开基站方向航行时，EWCFM-CME与FTR、REL相比，MAE分别提升69.11%、62.18%，RMSE分别提升67.86%、61.11%。

● 对于固定位置海上无线通信信道衰落，EWCFM-CME与FTR、REL相比，迭代次数分别减少81.71%、56.56%，算法运行时间分别减少81.46%、67.80%；离开基站方向航行时，EWCFM-CME与FTR、REL相比，迭代次数分别减少81.23%、57.38%，算法运行时间分别减少81.24%、65.65%。

基于舰船基站固定位置海上无线通信信道衰落数据集，采用Rayleigh、Rician、Nakagami、韦伯（Weibull）、双波扩散功率（two-wave with diffuse-power，TWDP）、高斯（Gaussian）不同概率分布函数生成测试数据，不同概率分布模型与海上无线通信信道衰落相似性见表4。

仿真实验结果表明如下。

● Rayleigh和Gaussian分布模型在海上无线通信信道衰落分布相似性较低。

● 在不同分布衰落环境中，Rician分布MAE达到0.645，比Nakagami、Weibull和TWDP分别提高10.26%、20.56%、14.36%；Rician分布RMSE达到0.735，比Nakagami、Weibull、TWDP分别提高8.89%、13.95%、12.56%。

● 海上无线通信信道衰落在小尺度上的分布是以Rician为主导，Nakagami、Weibull和TWDP多种分布共存的状态。

表4 不同概率分布模型与海上无线通信信道衰落相似性

4.2 EWCFM-CME与经典搜索算法性能分析

基于实验1中舰船与基站相对静止仿真实验数据，以最优解平均MAE、优解获得概率、解空间搜索覆盖率、收敛时间等为评价指标，将EWCFM-CME模型求解算法与布谷鸟搜索、遗传搜索、贝叶斯概率估计、梯度下降、模拟退火算法进行对比分析，EWCFM-CME与经典搜索算法最优解适应度如图9所示，海上无线衰落模型参数见表5。

图9 EWCFM-CME与经典搜索算法最优解适应度

表5 海上无线衰落模型参数

仿真实验结果表明如下。

● 贝叶斯概率估计和梯度下降为线性空间搜索，较大概率不能获得最优解。

● EWCFM-CME与布谷鸟搜索、遗传算法、模拟退火相比，最优解平均MAE分别提升10.39%、15.33%、11.56%，MAE达到0.9概

率分别提升10.28%、15.15%、11.57%。

● EWCFM-CME与布谷鸟搜索、遗传算法、模拟退火相比，收敛时间分别减少75.35%、39.54%、43.50%，算法运行时间分别减少60.48%、45.18%、43.23%；解空间搜索覆盖率分别提升79.06%、20.56%、43.23%，测试运行时间分别减少69.49%、77.35%、63.23%。

● 解空间具有周期性的波峰和波谷，传送布谷鸟搜索、遗传算法、模拟退火算法采用了线性步长进行搜索，容易导致特征消失或局部最优，搜索效率降低；采用改进蜂群求解算法的EWCFM-CME模型使用sin(·)函数为算子替换了线性步长，允许在步长间隔内随机取值，避免了因解空间的周期性导致特征消失和陷入局部最优的问题，提高了搜索效率。

综上，EWCFM-CME与布谷鸟搜索、遗传算法、模拟退火相比，精度平均分别提升10.32%、15.15%、11.57%，搜索时间分别减少60.48%、45.18%、43.23%。

5 结束语

针对海上无线通信信道在诸多复杂环境因素影响下，如何精确表征其衰落变化的问题，提出复杂气象环境下海上无线通信信道衰落估计模型（EWCFM-CME）。通过构建直射、镜面反射和漫反射路径的衰落模型，融合晴雨雪雾和雨雪混合气象环境因素影响，构建复杂气象环境下海上无线通信信道衰落估计模型。设计改进蜂群算法对其求解，核心思想是以引领蜂为中心，通过构建以sin(·)函数为算子引导跟随蜂进行搜索，降低搜索空间，提高求解效率和精度；以侦查蜂解集的均方差判断其解的准确度，避免因求解误差导致的算法抖动；引领蜂以概率接收侦查蜂解，将该侦查蜂更新为新的引领蜂，抑制引领蜂更新时容易陷入局部最优的问题。仿真实验结果表明，EWCFM-CME模型与FTR和REL相比，EWCFM-CME模型平均精度提升13.58%和11.43%；EWCFM-CME与布谷鸟搜索、遗传算法、模拟退火相比，精度平均提升10.32%、15.15%、11.57%，搜索时间减少60.48%、45.18%、43.23%；EWCFM-CME模型能有效表征不同气象环境海上无线通信信道衰落特征。EWCFM-CME模型可应用于对不同海上无线通信信道衰落环境的仿真，提供了一种有效的海上无线通信信道衰落建模与估计方法。

[1] YANG K, MOLISCH A F, EKMAN T, et al. A round earth loss model and small-scale channel properties for open-sea radio propagation[J]. IEEE Transactions on Vehicular Technology, 2019, 68(9): 8449-8460.

[2] 陈真佳. 海上电磁频谱感知与预测方法研究[D]. 海口: 海南大学, 2020.

CHEN Z J. Research on offshore electromagnetic spectrum sensing and prediction methods[D]. Haikou: Hainan University, 2020.

[3] 陈灿彬. 海上宽带移动无线信道建模研究[D]. 厦门: 厦门大学, 2017.

CHEN C B. Research on broadband mobile wireless channel modeling at sea surface[D]. Xiamen: Xiamen University, 2017.

[4] WANG J, ZHOU H F, LI Y, et al. Wireless channel models for maritime communications[J]. IEEE Access, 2018(6): 68070-68088.

[5] ROMERO-JEREZ J M, LOPEZ-MARTINEZ F J, PARIS J F, et al. The fluctuating two-ray fading model: statistical characterization and performance analysis[J]. IEEE Transactions on Wireless Communications, 2017, 16(7): 4420-4432.

[6] LEE J H, CHOI J, LEE W H, et al. Measurement and analysis on land-to-ship offshore wireless channel in 2.4 GHz[J]. IEEE Wireless Communications Letters, 2017, 6(2): 222-225.

[7] 王峰, 吴畏, 彭茜, 等. 海上VHF/UHF频段信道环境及其空时频率选择性[J]. 电子学报, 2017, 45(6): 1523-1529.

WANG F, WU W, PENG Q, et al. Maritime wireless channel environment at VHF/UHF bands and its space-time frequency selectivity[J]. Acta Electronica Sinica, 2017, 45(6): 1523-1529.

[8] WANG W, JOST T, RAULEFS R. A semi-deterministic path loss model for in-harbor LoS and NLoS environment[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(12): 7399-7404.

[9] YU H, SHUI P L, LU K. Outlier-robust tri-percentile parameter estimation of K-distributions[J]. Signal Processing, 2021(181): 107906.

[10] 魏特, 王文浩, 陈军, 等. 环境信息辅助的海上无线信道测量与建模[J]. 清华大学学报(自然科学版), 2021, 61(9): 1002-1007.

WEI T, WANG W H, CHEN J, et al. Environmental information-aided maritime wireless channel measurement and modelling[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(9): 1002-1007.

[11] HUO Y, DONG X, BEATTY S. Cellular communications in ocean waves for maritime internet of things[J]. IEEE Internet of Things Journal, 2020, 10(7): 9965-9979.

[12] 沈轩帆, 廖勇, 代学武, 等. 基于BEM的非平稳双选信道估计方法[J]. 电子学报, 2019, 47(1): 204-210.

SHEN X F, LIAO Y, DAI X W, et al. Non-stationary and doubly-selective channel estimation method based on basis expansion model[J]. Acta Electronica Sinica, 2019, 47(1): 204-210.

[13] 华博宇, 朱秋明, 何小祥, 等. 快速时变场景下非平稳衰落信道建模仿真[J]. 电信科学, 2020, 36(5): 56-64.

HUA B Y, ZHU Q M, HE X X, et al. Modeling and simulation of the non-stationary fading channels under fast time-variant environment[J]. Telecommunications Science, 2020, 36(5): 56-64.

[14] ABDULRAHMAN A Y, RAHMAN T A, RAHIM S K A, et al. Rain attenuation predictions on terrestrial radio links: differential equations approach[J]. Transactions on Emerging Telecommunications Technologies, 2012, 23(3): 293-301.

[15] CHEFFENA M, MOHAMED M. Empirical path loss models for wireless sensor network deployment in snowy environments[J]. IEEE Antennas and Wireless Propagation Letters, 2017(16): 2877-2880.

[16] FERREIRA M M, AMBROZIAK S J, CARDOSO F D, et al. Fading modeling in maritime container terminal environments[J] IEEE Transactions on Vehicular Technology, 2018, 67(10): 9087-9096.

[17] LIU Y, WANG C X, CHANG H, et al. A novel non-stationary 6G UAV channel model for maritime communications[J]. IEEE Journal on Selected Areas in Communications, 2021, 39(10): 2992-3005.

[18] YUE D W, ZHANGY, JIA Y. Beamforming based on specular component for massive MIMO systems in ricean fading[J]. IEEE Wireless Communications Letters, 2015, 4(2): 197-200.

[19] 商德江, 钱治文, 何元安, 等. 基于联合波叠加法的浅海信道下圆柱壳声辐射研究[J]. 物理学报, 2018, 67(08):125-138.

SHANGD J, QIANZ W, HE Y A, et al. Sound radiation of cylinder in shallow water investigated by combined wave superposition method[J]. Chinese Journal of Physics, 2018, 67(8): 125-138.

[20] 张颖, 姚雨丰. 基于快速贝叶斯匹配追踪优化的海上稀疏信道估计方法[J]. 电子与信息学报, 2020, 42(2): 534-540.

ZHANG Y, YAO Y F. Channel estimation algorithm of maritime sparse channel based on fast bayesian matching pursuit optimization[J]. Journal of Electronics & Information Technology, 2020, 42(2):534-540.

[21] 樊昌信, 曹丽娜. 通信原理(第7版)[M]. 北京: 国防工业出版社, 2012.

FAN C X, CAO L N. Principles of communication (7th edition)[M]. Beijing: National Defense Industry Press, 2012.

Estimation of wireless channel fading model in maritime communication for complex meteorological environment

DAI Yasheng1,2, MA Bolin1, YUE Guangxue1

1. College of Information Science and Technology, Jiaxing University, Jiaxing 314001, China 2. School of Computer Engineering and Science, Shanghai University, Shanghai 200444, China

Due to the influence of complex marine environmental factors such as sparse scattering of electromagnetic wave on the ocean surface, wave shadow fading, complex meteorological environment. It is extremely hard to model the fading of wireless channel in maritime communication environment. After analyzing the influence of meteorological environment and multipath channel fading via direct-path, specular-path and diffuse-path on marine wireless communication channel fading, the estimation of wireless channel fading model in maritime communication for complex meteorological environment (EWCFM-CME) was proposed. An improved bee colony algorithm was designed to estimation the parameter of EWCFM-CME. In order to improve the efficiency and accuracy of search algorithm, an iterative function with sin(·) function as operator was designed in search scheme of bee colonies. The leading bee received the detection bee solution to update itself with probability. It prevents the solution algorithm from falling into local optimization. The simulation results show that, compared with fluctuate two-ray (FTR) fading model and round earth loss (REL) model, the mean absolute error (MAE) of EWCFM-CME increased by 13.58% and 11.43% By comparing EWCFM-CME with cuckoo search, genetic algorithm and simulated annealing algorithm, the search time is reduced by 60.48%, 45.18% and 43.23%, respectively.

marine environment, wireless communication, bee colony algorithm, channel fading

TP393

10.11959/j.issn.1000−0801.2022061

2021−10−05；

2022−03−15

乐光学，gxyue@zjxu.edu.cn

国家自然科学基金资助项目（No.U19B2015）

The National Natural Science Foundation of China (No.U19B2015)